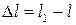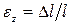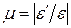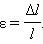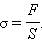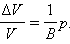деформация отношение удлинения элемента к первоначальной его длине
Коэффициент Пуассона. Связь продольной и поперечной деформации
Пусть в результате деформации первоначальная длина стержня l станет равной. l1. Изменение длины
называется абсолютным удлинением стержня.
При растяжении продольная деформация считается положительной, а при сжатии – отрицательной.
Поперечные размеры стержня в результате деформирования также изменяются, при этом при растяжении они уменьшаются, а при сжатии – увеличиваются. Если материал является изотропным, то его поперечные деформации равны между собой:
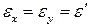
Опытным путем установлено, что при растяжении (сжатии) в пределах упругих деформаций отношение поперечной деформации к продольной является постоянной для данного материала величиной. Модуль отношения поперечной деформации к продольной, называемый коэффициентом Пуассона или коэффициентом поперечной деформации, вычисляется по формуле:
Для различных материалов коэффициент Пуассона изменяется в пределах 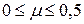
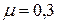
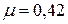
Деформация отношение удлинения элемента к первоначальной его длине
В твердых телах – аморфных и кристаллических – частицы (молекулы, атомы, ионы) совершают тепловые колебания около положений равновесия, в которых энергия их взаимодействия минимальна. При увеличении расстояния между частицами возникают силы притяжения, а при уменьшении – силы отталкивания (см. §3.1). Силы взаимодействия между частицами обусловливают механические свойства твердых тел.
Деформация твердого тела является результатом изменения под действием внешних сил взаимного расположения частиц, из которых состоит тело, и расстояний между ними.
Существует несколько видов деформаций твердых тел. Некоторые из них представлены на рис. 3.7.1.
Отношение абсолютного удлинения к первоначальной длине образца называется относительным удлинением или относительной деформацией :
|
Если принять направление внешней силы, стремящейся удлинить образец, за положительное, то при деформации растяжения и – при сжатии. Отношение модуля внешней силы к площади сечения тела называется механическим напряжением :
|
За единицу механического напряжения в СИ принят паскаль (). Механическое напряжение измеряется в единицах давления.
Материалы, у которых разрушение происходит при деформациях, лишь незначительно превышающих область упругих деформаций, называются хрупкими (стекло, фарфор, чугун).
На рис. 3.7.1 (3) показана деформация всестороннего сжатия твердого тела, погруженного в жидкость. В этом случае механическое напряжение совпадает с давлением в жидкости. Относительная деформация определяется как отношение изменения объема к первоначальному объему тела. При малых деформациях
|
Величина модуля всестороннего сжатия определяет скорость звука в данном веществе (см. §2.7).
Образовательный портал
К механическим свойствам металлов относят их способность сопротивляться деформациям (изменению формы или размеров) и разрушению под действием внешних нагрузок. Такими свойствами являются прочность, пластичность, твердость, вязкость (ударная), усталость, ползучесть.
Деформации, которые исчезают после снятия нагрузки, при этом материал принимает первоначальную форму, называют упругими. Деформации, которые остаются после снятия нагрузки, называют остаточными.
Для определения механических свойств материалов специальные образцы или готовые изделия испытывают в соответствии с требованиями ГОСТов. Испытания образцов могут быть статическими, когда на образец действует постоянная или медленно возрастающая нагрузка, динамическими, когда на образец действует мгновенно возрастающая (ударная) нагрузка, и повторно-переменными (усталостными), при которых нагрузка на образец многократно изменяется по величине и направлению.
В зависимости от характера действия приложенных к образцу или изделию сил (нагрузок) различают деформации сжатия, растяжения, изгиба, сдвига (среза), кручения.
Виды деформаций металла в зависимости от направления действующей нагрузки:
а — сжатия, б — растяжения, в — изгиба, г — сдвига (среза), д — кручения
Механические свойства оцениваются численным значением напряжения.
Напряжение — мера внутренних сил, возникающих в образце под влиянием внешних воздействий (сил, нагрузок).
Напряжение служит для оценки нагрузки, не зависящей от размеров деформируемого тела. Напряжения, действующие вдоль оси образца, называют нормальными и обозначают буквой σ (сигма).
Нормальные напряжения определяются отношением сил, действующих вдоль оси детали или образца, к площади их поперечного сечения:
σ = P/F,
где σ — нормальное напряжение, Па (1 Па = H/м²; 1 кгс/см² = 10 5 Па);
P — сила, действующая вдоль оси образца, H;
F — площадь поперечного сечения образца, м².
Нормальные напряжения в зависимости от направления действующих нагрузок бывают сжимающими и растягивающими.
Напряжения, действующие перпендикулярно оси образца, называют касательными и обозначают буквой τ.
Под действием касательных напряжений происходит деформация среза.
Напряжения определяют при механических испытаниях образцов на специальных машинах. Эти напряжения используют при расчетах деталей машин на прочность.
Усилия, нагрузки, действующие на детали, создают в них напряжения, которые в свою очередь вызывают деформацией деталей.
Например, канат автомобильного крана при поднятии груза под действием растягивающей нагрузки испытывает напряжение растяжения, поэтому и подвергается деформации растяжения. Под действием сжимающих напряжений деформацию сжатия испытывают станины и фундаменты станков, опорные колонны, колеса и катки машин. В стреле автомобильного или башенного крана, поднимающего груз, возникают напряжения изгиба, которые вызывают деформацию изгиба стрелы. Деформации изгиба испытывают балки, на которые положен груз, рельсы под тяжестью
поезда, башенного или козлового крана. На срез работают заклепочные соединения, стопорные болты.
Напряжения кручения вызывают деформацию кручения, например, когда у стяжных болтов
затягивают гайки.
Прочность — способность металлов или сплавов сопротивляться разрушению при действии внешних сил, вызывающих внутренние напряжения и деформации.
В зависимости от характера действия внешних сил различают прочность на растяжение, сжатие, изгиб, кручение, ползучесть и усталость.
Определение характеристик прочности при растяжении — наиболее важный и распространенный вид механических испытаний металлов. Испытывают образцы определенной формы и размеров на специальных разрывных машинах (ГОСТ 1497—73). Стандартный образец (рис. Стандартный образец для испытания на растяжение) закрепляют головками в машине и медленно нагружают с постоянной скоростью.
В результате возрастающей нагрузки происходит растяжение образца вплоть до разрушения.
При испытании производится автоматическая запись диаграммы растяжения, представляющей собой график изменения абсолютной длины образца в зависимости от приложенной нагрузки.
Определенные точки на диаграмме растяжения p, c, s, b отражают наиболее важные характеристики прочности: предел пропорциональности, условные пределы упругости, текучести и прочности.
Предел пропорциональности σ пц (точка p на диаграмме растяжения) — это наибольшее напряжение, возникающее под действием нагрузки P пц, до которого деформации в металле растут прямо пропорционально нагрузке. При этом в образце происходят только упругие деформации, т.е. образец после снятия нагрузки принимает свои первоначальные размеры. При дальнейшем увеличении нагрузки деформации образца будут остаточными.
Условный предел упругости σ 0,05 (точка c на диаграмме растяжения) — это напряжение, при котором образец получает остаточное удлинение, равное 0,05% первоначальной длины образца.
Практически предел упругости очень близок пределу пропорциональности.
Условный предел текучести (точка s на диаграмме растяжения) — это напряжение, при котором остаточное
удлинение достигает заданного значения, обычно 0,2%, но иногда 0,1 или 0,3% и более при нагрузках Рt.
В соответствии с этим условный предел текучести обозначается σ 0,2, σ о,1, σ 0,3 и т. д.
Следовательно, условный предел текучести отличается от условного предела упругости только заданным значением остаточного удлинения.
Условный предел текучести соответствует напряжению, при котором происходит наиболее полный переход к пластической деформации металла.
Условный предел прочности σ в (точка b на диаграмме растяжения) — это условное наибольшее напряжение, при котором происходит наибольшая равномерная по всей длине деформация образца.
После точки s на участке sb диаграммы растяжения при дальнейшем увеличении нагрузки в образце развивается интенсивная пластическая деформация. До точки b образец удлиняется равномерно по всей длине. В точке b начинается резкое уменьшение поперечного сечения образца на коротком участке с образованием так называемой шейки.
Предел прочности определяют по формуле:
σ в = Pв/Fo,
где σ в — предел прочности материала, Па;
Pв — нагрузка в точке b, H;
Fo — площадь поперечного сечения образца до испытания, м².
Характеристиками прочности пользуются при изготовлении деталей машин. Практическое значение пределов пропорциональности, упругости и текучести сводится к тому, чтобы определить численное значение напряжений, под действием которых могут работать детали машинах, не подвергаясь остаточной деформации (предел пропорциональности) или подвергаясь деформации на небольшую допустимую величину σ 0,о5, σ о,2 и т. д.
Пластичность — способность металлов сохранять изменение формы, вызванное действием деформирующих сил после того, как силы сняты.
Пластические свойства испытываемого образца металла определяют при испытаниях на растяжение. Под действием нагрузки образцы удлиняются, при этом поперечное сечение их соответственно уменьшается. Чем больше удлиняется образец при испытании, тем более пластичен материал. Характеристиками пластичности материалов служат относительное удлинение и относительное сужение образцов.
Относительным удлинением называется отношение приращения длины образца после разрыва к его перво-
начальной длине.
Относительное удлинение δ (дельта) выражают в процентах и вычисляют по формуле:
δ = [ (l1 — l0)/l0 ] • 100%
где l1 — длина образца после разрыва, м;
l0 — длина образца до начала испытания, м.
Относительным сужением называется отношение уменьшения площади поперечного сечения образца после разрыва к площади поперечного сечения образца до начала испытания.
Относительное сужение ψ (пси) выражают в процентах и вычисляют по формуле
ψ = [ (F0 — F1)/F0 ] • 100%
где F0 — площадь поперечного сечения образца до начала испытания, м²;
F1 — площадь поперечного сечения образца после разрыва, м².
Твердость — сопротивление поверхностных слоев материала местным деформациям.
Твердость обычно оценивается сопротивлением вдавливанию в поверхность металла индикатора из более твердого материала.
Измерение твердости металлов и сплавов как метод щенки их механических свойств широко используется в технике.
По твердости судят о других свойствах металла и сплава. Например, для многих сплавов, чем выше твердость, тем больше прочность на растяжение, выше износостойкость; как правило, сплавы с меньшей твердостью легче обрабатываются резанием.
Твердость определяют непосредственно на деталях без их разрушения. Поэтому испытание на твердость является незаменимым производственным методом оценки механических свойств материалов.
На практике в зависимости от используемого прибора твердость определяют двумя способами. Если твердость исследуемого материала меньше, чем твердость закаленной стали, то используют твердомер шариковый — ТШ, если твердость исследуемого материала больше, чем твердость закаленной стали, то пользуются твердомером конусным — ТК.
При определении твердости по Бринеллю на приборах ТШ (ГОСТ 9012—59) стальной закаленный шарик диаметром D (2,5; 5 или 10 мм) вдавливают в испытуемый металл под действием нагрузки P в течение определенного времени.
После удаления нагрузки на поверхности испытуемого металла остается отпечаток.
Измерив под микроскопом диаметр отпечатка а, по таблицам стандарта определяют твердость металла.
Отношение приложенной к шарику нагрузки (кгс) к площади поверхности отпечатка шарика (мм²) называется числом твердости по Бринеллю и обозначается HB.
Если на шарик диаметром 0-10 мм действует нагрузка Р=3000 кгс в течение 10 с, то определяемое по таблицам число твердости по Бринеллю записывают так: HВ400, HВ250, HВ500 и т. д.
При других условиях испытания к обозначению НВ добавляют цифры, характеризующие диаметр шарика (мм), нагрузку (кгс) и продолжительность выдержки (с).
Например, HВ5/750/30—350 обозначает, что число твердости по Бринеллю равно 350 при испытании вдавливанием шарика диаметром D = 5 мм под нагрузкой Р = 750 кгс в течение t = 30 с.
При определении твердости по Роквеллу на приборах ТК (ГОСТ 9013—59) алмазный конус с углом при вершине 120° вдавливают в испытуемый металл сначала под действием предварительной нагрузки Р0, равной
10 кгс, которая не снимается до конца испытания.
Под нагрузкой Р0 алмазный конус вдавливается на глубину h0. Затем к предварительной нагрузке добавляется основная нагрузка Р1, равная 140 или 50 кгс — для очень твердых и хрупких материалов. Алмазный конус вдавливается на глубину h1. Через 1 — 3 с, после того как стрелка прибора замедлит свое движение, основную нагрузку снимают. Стрелка прибора показывает на шкале твердость металла в условных единицах.
За условную единицу твердости по Роквеллу принимается глубина вдавливания алмазного конуса на величину 0,002 мм ≈ h0. Все шкалы прибора отградуированы в безразмерных условных единицах твердости.
Твердость, определяемая на приборах ТК. методом вдавливания алмазного конуса, называется твердостью по Роквеллу и обозначается НR. Отсчет твердости ведут по двум шкалам в зависимости от применяемой общей нагрузки Р.
Если Р = Р0 + Р1= 10 + 140= 150 кгс, то отсчет твердости ведут по шкале С и твердость обозначают НРС, если Р = Ро+Р1 = 10+50 = 60 кгс, то отсчет твердости ведут также по шкале С, но твердость обозначают НРА.
Если необходимо измерить твердость по Роквеллу мягких материалов, то алмазный конус заменяют шариком диаметром 1,6 мм. Основная нагрузка Р1 = 90 кгс, значит, общая нагрузка Р = Р0 + Р1 = 10 + 90 = 100 кгс.
Отсчет твердости ведут по специальной шкале B, а твердость обозначают НRB.
Твердость по Роквеллу НR записывают таким образом:
HRC65, HRB30, HRA80 и т. д., где цифры обозначают твердость, а буквы А, С, В — соответствующую шкалу.
Ударная вязкость — способность металлов сопротивляться действию ударных нагрузок. При ударных нагрузках напряжения, возникающие в металле, действуют мгновенно, поэтому их трудно определить. Ударную вязкость определяют работой, затраченной на излом образца.
Для определения ударной вязкости при нормальной температуре (ГОСТ 9454—78) предусмотрено 20 типоразмеров образцов квадратного и прямоугольного сечения. Чаще применяют образцы квадратного сечения 10 х 10 мм длиной 55 мм с концентратором (надрезанные с одной стороны посередине длины на глубину 2 мм).
Образец 1 стандартной формы
укладывают горизонтально в специальный шаблон маятникового копра, обеспечиваюший установку надреза образца строго в середине пролета между опорами 3. Маятник 2 копра закрепляется в исходном верхнем положении на высоте H.
Работа, затраченная на разрушение образца, определяется разностью потенциальных энергий маятника в начальный (после подъема на угол α) и конечный моменты испытания (после взлета на угол β) и выражается формулой:
k = P (H — h)
k — работа, затраченная на разрушение образца, Дж (кгс · м)
Р — вес маятника, кгс
H и h — высоты подъема и взлета маятника, м
Основную характеристику при испытании на ударную вязкость — определяют по формуле:
kcu = k/So
kc — ударная вязкость, Дж/м² (1 Дж/м² ≈ 0,1 кгс · м/см²)
u — форма концентратора
So — площадь поперечного сечения образца в месте надреза до испытания, м²
Многие детали машин и конструкции во время работы подвергаются ударным нагрузкам, действие которых на детали происходит мгновенно. В результате изменяются условия, при которых работают такие детали.
Ударные нагрузки испытывают инструменты типа штампов. некоторые зубчатые передачи и т.д.
Усталость — разрушение металлов под действием многократных повторно-переменных (циклических) нагрузок, при напряжениях меньших предела прочности на растяжение.
В условиях действия повторно-переменных нагрузок в работающих деталях образуются и развиваются трещины, которые приводят к полному разрушению деталей. Подобное разрушение опасно тем, что может происходить под действием напряжений, намного меньших пределов прочности и текучести.
Свойство противостоять усталости называется выносливостью. Сопротивление усталости характеризуется пределом выносливости, т. е. наибольшим напряжением, которое может выдержать металл без разрушения заданное число раз.
Под действием повторно-переменных нагрузок работают коленчатые валы двигателей, многие детали машин — валы, шатуны, пальцы, шестерни и т. д.
Цель испытаний на усталость (ГОСТ 2860-65) — количественная оценка способности материала (образца) работать при повторно-переменных нагрузках без разрушения.
Цикл напряжений — совокупность переменных значений напряжении за один перепад их изменения. Заданное число циклов нагружения при испытании называют базой испытания. Обычно база испытания составляет 10 8 циклов нагружения. Если материал выдержал базовое число циклов без разрушения, то он хорошо противостоит усталости и деталь из этого материала будет работать надежно.
Ползучесть — способность металлов и сплавов медленно и непрерывно пластически деформироваться под действием постоянной, длительно действующей нагрузки.
Изделия из металлов и сплавов, работающие при повышенных или высоких температурах, обладают меньшей прочностью. При эксплуатации любой материал под действием постоянной нагрузки (напряжения) может в определенных условиях прогрессивно деформироваться с течением времени.
Испытания на ползучесть при растяжении (ГОСТ 3248-60) заключаются в том, что испытуемый образец в течение длительного времени подвергается действию постоянного растягивающего усилия при постоянной высокой температуре.
В результате испытания определяют предел ползучести металла, т. е. наибольшее растягивающее напряжение, при котором скорость ползучести или относительное удлинение за определенный промежуток времени достигает заданной величины.
Если задаются скоростью ползучести, то предел ползучести обозначают σνп,
где νп — заданная скорость ползучести, %/ч; t — температура испытания, °С.
Если задаются относительным удлинением, то в обозначении предела ползучести используют три индекса:
температуру испытания t, °С
относительное удлинение σ, %
продолжительность испытания τ, ч
Например, 
Сила упругости
Сила: что это за величина
В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или тормозит, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.
Сила — это физическая векторная величина, которую воздействует на данное тело со стороны других тел.
Она измеряется в Ньютонах — это единица измерения названа в честь Исаака Ньютона.
Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.
Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.
Деформация
Деформация — это изменение формы и размеров тела (или части тела) под действием внешних сил
Происходит деформация из-за различных факторов: при изменении температуры, влажности, фазовых превращениях и других воздействиях, вызывающих изменение положения частиц тела.
Деформация является деформацией, пока сила, вызывающая эту деформацию, не приведет к разрушению.
На появление того или иного вида деформации большое влияние оказывает характер приложенных к телу напряжений. Одни процессы деформации связаны с преимущественно перпендикулярно (нормально) приложенной силой, а другие — преимущественно с силой, приложенной по касательной.
По характеру приложенной к телу нагрузки виды деформации подразделяют следующим образом:
Сила упругости: Закон Гука
Деформацию тоже можно назвать упругой (при которой тело стремится вернуть свою форму и размер в изначальное состояние) и неупругой (когда тело не стремится вернуться в исходное состояние).
При деформации возникает сила упругости— это та сила, которая стремится вернуть тело в исходное состояние, в котором оно было до деформации.
Сила упругости, возникающая при упругой деформации растяжения или сжатия тела, пропорциональна абсолютному значению изменения длины тела. Выражение, описывающее эту закономерность, называется законом Гука.
Закон Гука
Fупр = kx
Fупр — сила упругости [Н]
k — коэффициент жесткости [Н/м]
х — изменение длины (деформация) [м]
Изменение длины может обозначаться по-разному в различных источниках. Варианты обозначений: x, ∆x, ∆l.
Это равноценные обозначения — можно использовать любое удобное.
Поскольку сила упругости направлена против направления силы, с которой это тело деформируется (она же стремится все «распрямить»), в Законе Гука должен быть знак минус. Часто его и можно встретить в разных учебниках. Но поскольку мы учитываем направление этой силы при решении задач, знак минус можно не ставить.
Задачка
На сколько удлинится рыболовная леска жесткостью 0,3 кН/м при поднятии вверх рыбы весом 300 г?
Решение:
Сначала определим силу, которая возникает, когда мы что-то поднимаем. Это, конечно, сила тяжести. Не забываем массу представить в единицах СИ – килограммах.
Если принять ускорение свободного падения равным 10 м/с*с, то модуль силы тяжести равен :
Тогда из Закона Гука выразим модуль удлинения лески:
Выражаем модуль удлинения:
Подставим числа, жесткость лески при этом выражаем в Ньютонах:
x=3/(0,3 * 1000)=0,01 м = 1 см
Ответ: удлинение лески равно 1 см.
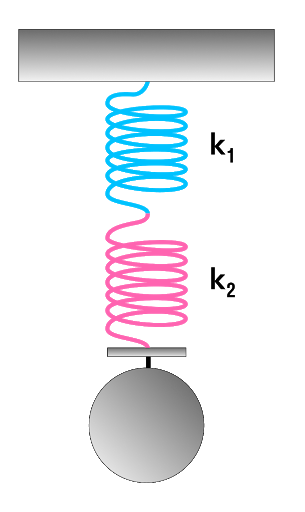
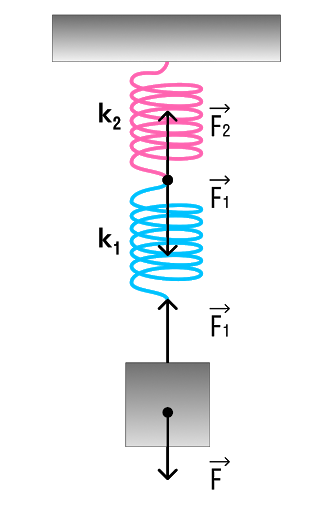
Параллельное и последовательное соединение пружин
В Законе Гука есть такая величина, как коэффициент жесткости— это характеристика тела, которая показывает его способность сопротивляться деформации. Чем больше коэффициент жесткости, тем больше эта способность, а как следствие из Закона Гука — и сила упругости.
Чаще всего эта характеристика используется для описания жесткости пружины. Но если мы соединим несколько пружин, то их суммарная жесткость нужно будет рассчитать. Разберемся, каким же образом.
Последовательное соединение системы пружин
Последовательное соединение характерно наличием одной точки соединения пружин.
При последовательном соединении общая жесткость системы уменьшается. Формула для расчета коэффициента упругости будет иметь следующий вид:
Коэффициент жесткости при последовательном соединении пружин
1/k = 1/k₁ + 1/k₂ + … + 1/k_i
k — общая жесткость системы [Н/м] k1, k2, …, — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе [-]
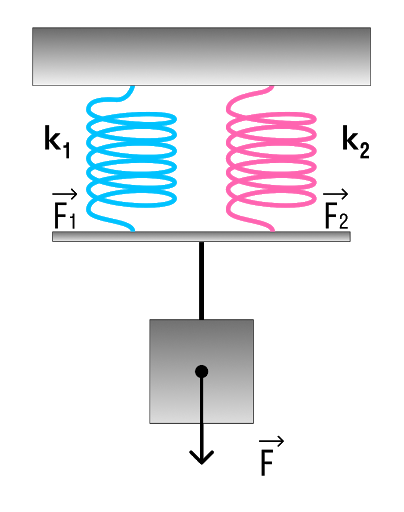
Параллельное соединение системы пружин
Последовательное соединение характерно наличием двух точек соединения пружин.
В случае когда пружины соединены параллельно величина общего коэффициента упругости системы будет увеличиваться. Формула для расчета будет выглядеть так:
Коэффициент жесткости при параллельном соединении пружин
k — общая жесткость системы [Н/м] k1, k2, …, ki — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе [-]
Задачка
Какова жесткость системы из двух пружин, жесткости которых k₁ = 100 Н/м, k₂ = 200 Н/м, соединенных: а) параллельно; б) последовательно?
Решение:
а) Рассмотрим параллельное соединение пружин.
При параллельном соединении пружин общая жесткость
k = k₁ + k₂ = 100 + 200 = 300 Н/м
б) Рассмотрим последовательное соединение пружин.
При последовательном соединении общая жесткость двух пружин
1/k = 1/100 + 1/200 = 0,01 + 0,005 = 0,015
k = 1000/15 = 200/3 ≃ 66,7 Н/м
График зависимости силы упругости от жесткости
Закон Гука можно представить в виде графика. Это график зависимости силы упругости от изменения длины и по нему очень удобно можно рассчитать коэффициент жесткости. Давай рассмотрим на примере задач.
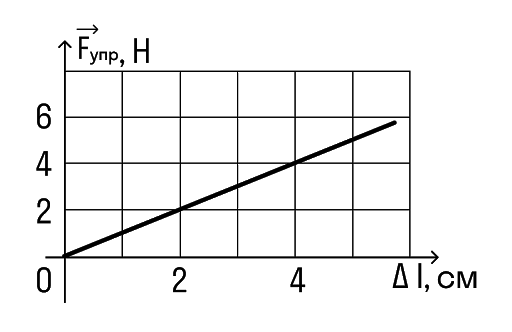
Задачка 1
Определите по графику коэффициент жесткости тела.
Решение:
Из Закона Гука выразим коэффициент жесткости тела:
Снимем значения с графика. Важно выбрать одну точку на графике и записать для нее значения обеих величин.
Например, возьмем вот эту точку.
В ней удлинение равно 2 см, а сила упругости 2 Н.
Переведем сантиметры в метры: 2 см = 0,02 м И подставим в формулу: k = F/x = 2/0,02 = 100 Н/м
Ответ:жесткость пружины равна 100 Н/м
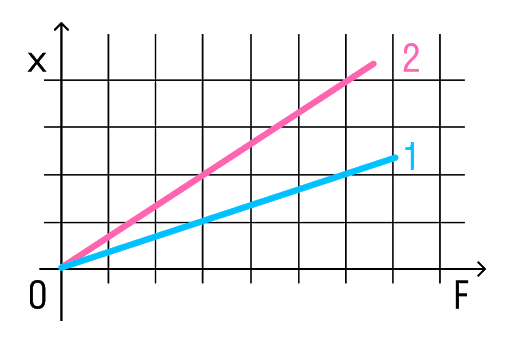
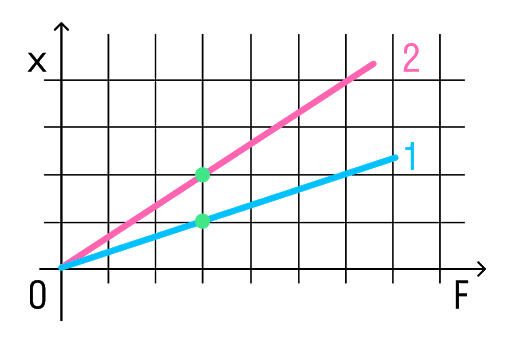
Задачка 2
На рисунке представлены графики зависимости удлинения от модуля приложенной силы для стальной (1) и медной (2) проволок равной длины и диаметра. Сравнить жесткости проволок.
Решение:
Возьмем точки на графиках, у которых будет одинаковая сила, но разное удлинение.
Мы видим, что при одинаковой силе удлинение 2 проволоки (медной) больше, чем 1 (стальной). Если выразить из Закона Гука жесткость, то можно увидеть, что она обратно пропорциональна удлинению.
Значит жесткость стальной проволоки больше.
Ответ: жесткость стальной проволоки больше медной.