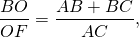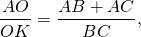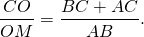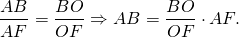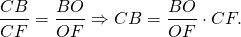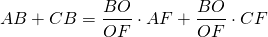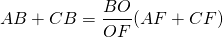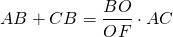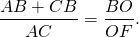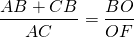деление биссектрис точкой пересечения в отношении
Элементы треугольника. Биссектриса
Биссектриса треугольника – отрезок биссектрисы угла треугольника, заключенный между вершиной треугольника и противолежащей ей стороной.
Свойства биссектрисы
1. Биссектриса треугольника делит угол пополам.
2. Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон ()
3. Точки биссектрисы угла треугольника равноудалены от сторон этого угла.
4. Биссектрисы внутренних углов треугольника пересекаются в одной точке — центре вписанной в этот треугольник окружности.
Некоторые формулы, связанные с биссектрисой треугольника
(доказательство формулы – здесь)
, где
— длина биссектрисы, проведённой к стороне
,
— стороны треугольника против вершин
соответственно,
— длины отрезков, на которые биссектриса
делит сторону
,
Приглашаю посмотреть видеоурок, в котором демонстрируется применение всех указанных выше свойств биссектрисы.
Задачи, рассматриваемые в видеоролике:
1.В треугольнике АВС со сторонами АВ=2 см, ВС=3 см, АС=3 см проведена биссектриса ВМ. Найти длины отрезков АМ и МС
2. Биссектриса внутреннего угла при вершине А и биссектриса внешнего угла при вершине С треугольника АВС пересекаются в точке М. Найдите угол BMC, если угол В равен 40, угол С – 80 градусов
3. Найти радиус окружности, вписанной в треугольник, считая стороны квадратных клеток равными 1
Возможно, вам будет интересен и этот небольшой видеоурок, где применяется одно из свойств биссектрисы
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Биссектриса треугольника делится в отношении
Выясним, в каком отношении точка пересечения биссектрис треугольника делит каждую биссектрису.
Каждая биссектриса треугольника делится точкой пересечения биссектрис в отношении суммы прилежащих сторон к противолежащей, считая от вершины.
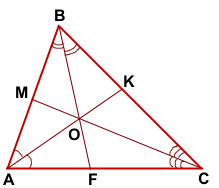
AK, BF, CM — биссектрисы ΔABC,
Из треугольника CBF по свойству биссектрисы треугольника
Разделив обе части равенства на AC, получим
Два другие соотношения доказываются аналогично.
Что и требовалось доказать.
Так как согласно неравенству треугольника длина любой стороны треугольника меньше суммы двух других его сторон, то каждое из этих отношений больше единицы.
Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении17:10, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 22.
AK, BF, CM — биссектрисы ΔABC,
AK∩BF=O, BO:OF=17:10, AC=22
(на экзамене в открытой части необходимо привести доказательство).
Определение и свойства биссектрисы угла треугольника
В данной публикации мы рассмотрим определение и основные свойства биссектрисы угла треугольника, а также приведем пример решения задачи, чтобы закрепить представленный материал.
Определение биссектрисы угла треугольника
Биссектриса угла – это луч, который берет начала в вершине угла и делит данный угол пополам.
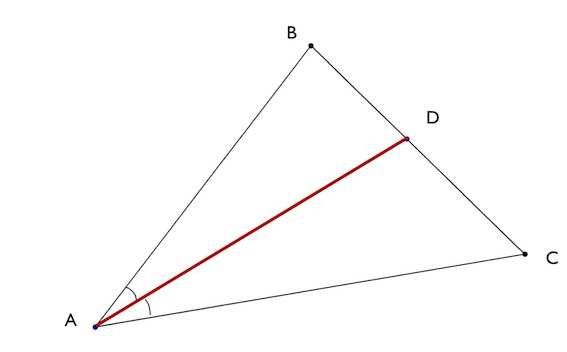
Биссектриса треугольника – это отрезок, соединяющий вершину угла треугольника с противоположной стороной и делящий этот угол на две равные части. Такая биссектриса, также, называется внутренней.
Основание биссектрисы – точка на стороне треугольника, которую пересекает биссектриса. Т.е. в нашем случае – это точка D.
Внешней называется биссектриса угла, смежного с внутренним углом треугольника.
Свойства биссектрисы треугольника
Свойство 1 (теорема о биссектрисе)
Биссектриса угла треугольника делит его противоположную сторону в пропорции, равной отношению прилежащих к данному углу сторон. Т.е. для нашего треугольника (см. самый верхний рисунок):
Свойство 2
Точка пересечения трех внутренних биссектрис любого треугольника (называется инцентром) является центром вписанной в фигуру окружности.
Свойство 3
Все биссектрисы треугольника в точке пересечения делятся в отношении, равном сумме прилежащих к углу сторон, деленной на противолежащую сторону (считая от вершины).
Свойство 4
Если известны длины отрезков, образованных на стороне, которую пересекает биссектриса, а также две другие стороны треугольника, найти длину биссектрисы можно по формуле ниже (следует из теоремы Стюарта):
BD 2 = AB ⋅ BC – AD ⋅ DC
Свойство 5
Внешняя и внутренняя биссектрисы одного и того же угла треугольника перпендикулярны друг к другу.
Пример задачи
Дан прямоугольный треугольник с катетами 6 см и 8 см. Найдите длину биссектрисы, проведенной к гипотенузе.
Решение
Нарисуем чертеж согласно условиям задачи.
Применив теорему Пифагора мы можем найти длину гипотенузы (ее квадрат равен сумме квадратов двух катетов).
BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100.
Следовательно, BC = 10 см.
Далее составляем пропорцию согласно Свойству 1, условно приняв отрезок BD на гипотенузе за “a” (тогда DC = “10-a”):
Избавляемся от дробей и решаем получившееся уравнение:
8a = 60 – 6a
14a = 60
a ≈ 4,29
Таким образом, BD ≈ 4,29 см, CD ≈ 10 – 4,29 ≈ 5,71 см.
Теперь мы можем вычислить длину биссектрисы, использую формулу, приведенную в Свойстве 4:
AD 2 = AB ⋅ AC – BD ⋅ DC = 6 ⋅ 8 – 4,29 ⋅ 5,71 ≈ 23,5.
Биссектриса угла, биссектриса треугольника: что это такое и в чем разница
Биссектриса угла – луч, исходящий из вершины угла и разделяющий его пополам.
Биссектриса треугольника – отрезок, проведенный от вершины угла до противолежащей стороны треугольника.
В треугольнике может быть только три (внутренних) биссектрисы, каждая из которых будет делить свою вершину на два равных угла.
Что означает слово «биссектриса»?
«Биссектриса» – слово латинского происхождения, состоящее из двух частей: «bi» – «пара, двойное» и «sectio» – «разрезать, делить».
Название отражает суть: деление чего-то пополам, то есть на две равные части. В случае биссектрисы в роли «чего-то» выступает угол, который она делит на два угла.
Если при упоминании биссектрисы вам на ум приходит «крыса, бегающая по углам и делящая их пополам» из известного двустишия, то в принципе это не будет ошибкой ее определения, с той лишь поправкой, что каждая такая «крыса» должна замереть в конкретном положении для заданного угла, чтобы каждая ее точка была равноудалена от сторон этого угла.
Свойства биссектрисы
Есть несколько качеств биссектрисы, по которым ее легко узнать или вычислить.
В любом треугольнике все три биссектрисы всегда будут пересекаться в одной и той же точке.
Точка пересечения биссектрис в треугольнике является центром вписанной в этот треугольник окружности.
В равнобедренном треугольнике биссектриса совпадает с медианой и высотой.
В равностороннем треугольнике (это равнобедренный треугольник с равными углами) все три биссектрисы являются высотами и медианами. Кроме того, все они – три биссектрисы, медианы и высоты – будут одной и той же длины.
И последнее по счету (но не по значению) свойство биссектрисы. Зная его, вы сможете решить большинство задач по геометрии, где нужно вычислить длины сторон треугольника.
Биссектриса делит противоположную своему углу сторону треугольника на два отрезка. И отношение длин этих отрезков (записывается в виде дроби) в точности равно отношению двух соседних сторон всего треугольника.
Применение биссектрисы на практике
Биссектриса не является лишь абстрактным математическим понятием. На самом деле без знания этого термина и его сути невозможно обойтись во многих сферах: при строительстве крыши, при защите радиовысотомеров от радиолокационных ракет, при конструировании кораблей, при исследовании следов орудий взлома и так далее.