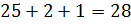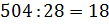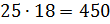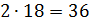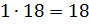деление числа в данном отношении 6 класс объяснение

Деление числа в данном отношении

На практике и в курсе математики довольно часто приходится делить число (величину) в данном отношении. Такие задачи решают на ЕГЭ, решали и в глубокой древности. Начнём с задачи из Древнего Египта.

Задача 1. Число и его половина составляют 9. Найдите число.

Решение. Пусть половина числа составляет 1 часть, тогда само число — 2 такие же части, так как число в 2 раза больше своей половины.

1) 1 + 2 = 3 (части) — приходится на число и его половину,

2) 9: 3 = 3 (единицы) — приходится на 1 часть, это половина числа,

3) 3 * 2 = 6 (единиц) — приходится на число.

Изменим условие задачи на части — получим задачу на деление числа в данном отношении.

Задача 2. Разделите число 9 в отношении 2: 1. Найдите полученные числа.

Решение задачи записано выше. Сделаем вывод в виде правила, которому можно следовать при решении других задач, меняя число и члены отношения.

Чтобы число 9 разделить в отношении 2: 1, надо это число разделить на сумму членов отношения и результат умножить на каждый член отношения.

Запишем решение задачи по новому правилу.

Решение. 1) 9: (2 + 1) * 2 = 6 — большее число,

2) 9: (2 + 1) * 1 = 3 — меньшее число.

Разумеется, меньшее число можно было найти вычитанием: 9 — 6 = 3.

Задача 3. Брат и сестра разделили 35 конфет в отношении 3: 4. Брату досталась меньшая часть. Сколько конфет досталось сестре?

Решение. 1) 35: (3 + 4) * 3 = 15 (конфет) — досталось брату,

2) 35 — 15 = 20 (конфет) — досталось сестре.

Задача 4. Малыш и Карлсон разделили 16 плюшек в отношении 3: 5. Сколько плюшек досталось Карлсону, если Малышу досталось меньше плюшек?

Решение. 1) 16: (3 + 5) * 3 = 6 (плюшек) — досталось Малышу,

2) 16 — 6 = 10 (плюшек) — досталось Карлсону.

Задача для ребят постарше.

Задача 5. В треугольнике три стороны имеют длину 8, 10 и 12. На какие отрезки биссектриса треугольника делит среднюю его сторону?

Решение. Биссектриса треугольника делит его сторону на части, пропорциональные двум другим сторонам треугольника, то есть в отношении 8: 12 = 2: 3. Разделим сторону 10 в отношении 2: 3.

1) 10: (2 + 3) * 2 = 4 — длина меньшей части,

2) 10 — 4 = 6 — длина большей части.

На ЕГЭ базового уровня в 2018 году была такая задача.

Задача 6. Маша и Медведь съели 110 печений и банку варенья, начав и закончив одновременно. Сначала Маша ела варенье, а Медведь — печенье, но в какой-то момент они поменялись. Медведь и то, и другое ест в три раза быстрее Маши. Сколько печений съел Медведь, если варенья они съели поровну?

Решение. Так как варенья они съели поровну, а Медведь ест варенье в 3 раза быстрее Маши, то на варенье Медведь потратил времени в 3 раза меньше, чем Маша. Печенье Медведь ел в 3 раза больше времени, чем Маша, которая в это время ела варенье. Так как скорость поедания печенья у Медведя в 3 раза больше, чем у Маши, то Медведь съел печенья в 3*3 = 9 раз больше, чем Маша. Делим 110 печений в отношении 9: 1.Медведь съел 110: (9 + 1)*9 = 99 (печений).

Авторы комментариев ФИПИ к результатам ЕГЭ отметили, что в группе хорошо подготовленных к сдаче экзамена на базовом уровне решили эту задачу менее половины выпускников, включенных в эту группу. При этом предполагалось, что задачу будут решать составлением уравнения. Как показано выше, задачу можно решить и арифметически.

Источник

Математика. 6 класс

Конспект урока

Деление числа в данном отношении

Перечень вопросов, рассматриваемых в теме:

Частное двух не равных нулю чисел a и b называется отношением чисел a и b.

Числа a и b называются членами отношения.

Скорость – это отношение пройденного пути ко времени, за которое этот путь пройден.

Скорость сближения – это расстояние, на которое сближаются объекты за единицу времени.

Цена товара – это отношение стоимости товара к его массе или количеству единиц товара.

Теоретический материал для самостоятельного изучения

Сегодня мы с вами разберём, что означает деление числа в данном отношении.

Правило деления числа в данном отношении.

Чтобы разделить число c в отношении a к b, можно разделить число c на сумму членов отношения a + b и результат умножить на каждый член отношения, числа a, b и c не равны нулю.

Ответ: конфеты между друзьями надо разделить так: первому – 16 конфет, а второму – 64 конфеты.

Сестра и брат сложили свои деньги для покупки лотерейного билета. У сестры было 50 рублей, а у брата 30 рублей. Билет выиграл 4000 рублей. Как они должны разделить эти деньги между собой?

Ответ: 2500 рублей, 1500 рублей.

Трое хотят купить фирму по продаже мороженого. Первый желает иметь 6 частей акций, второй – 4 части акций, третий – 2 части. Всего нужно заплатить 960 000 рублей. Сколько денег должен внести каждый из них.

Ответ: 480 000 рублей, 320 000 рублей, 160 000 рублей.

Первая машинистка печатает 180 страниц за 20 часов, а вторая – за 30 часов. Как распределить между ними 180 страниц, чтобы они напечатали их в кратчайший срок?

Ответ: первой машинистке – 108 страниц, второй – 72 страницы.

Мотоциклист может проехать расстояние между пунктами за 4 часа, а велосипедист – за 12 часов. Однажды они одновременно отправились навстречу друг другу из этих пунктов. Сколько километров проедет каждый до встречи, если расстояние между пунктами 120 километров?

Разбор решения заданий тренировочного модуля

№1. Тип задания: сортировка элементов по категориям.

Поставьте в соответствующие столбцы числа, которые можно разделить нацело в заданных отношениях.

№2. Тип задания: подчеркивания.

Нужно подчеркнуть правильный вариант ответа.

Источник

Конспект урока математики 6 класса по теме «Деление числа в данном отношении»

Ищем педагогов в команду «Инфоурок»

Тема. Деление числа в данном отношении.

ДАТА ПРОВЕДЕНИЯ: ________________

Научится делить число в данном отношении; формировать навыки решения задач по теме.

Развивать умение слушать; ясно, точно, грамотно излагать свои мысли в устной и письменной речи; развивать креативность мышления, инициативу, находчивость, активность при решении математических задач; формировать представления о математике как способе познания, сохранения и гармоничного развития мира, как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;

Развивать навыки мыслительных операций, умений обобщать, правильно формулировать задачи, выводы;

развивать умение работать с математическим текстом (анализировать, извлекать необходимую информацию); развивать представления о числе;

Формировать познавательный интерес к математике, ответственность, умение высказывать свои мысли, отстаивать свою точку зрения, слушая других;

Воспитывать культуру общения.

ВИД УРОКА : ____________________________________

ПРОДОЛЖИТЕЛЬНОСТЬ: 45 минут .

Формы работы учащихся : индивидуальная, групповая.

Проверка домашнего задания.

Устное решение упражнений.

Отношение величин (5 заданий) (Каждое задание по 1 баллу)

1. Чем является отношение величин одного наименования? (Ответ: число).

2. Найдите отношение величин . (Ответ: 20).

3. Упростите отношение величин . (Ответ: 200).

4. Упростите отношение величин . (Ответ: 40).

5. Упростите отношение величин . (Ответ: ).

Объяснение нового материала.

Деление числа в данном отношении.

Рассмотрим такую задачу. Пусть требуется разделить между двумя друзьями 60 конфет в отношении 2 : 3.

1 друг – ? конфет

1) 2 + 3 = 5 (частей) – составляют все конфеты;

2) 60 : 5 = 12 (конфет) – приходится на 1 часть;

3) 2  12 = 24 (конфеты) – приходится на 2 части, это для 1 друга;

4) 3  12 = 36 (конфет) – приходится на 3 части, это для 2 друга.

Решим эту же задачу по другому.

1) (конфеты) – приходится на 2 части, это для 1 друга;

2) (конфет) – приходится на 3 части, это для 2 друга.

Ответ : 24 конфеты, 36 конфет.

Таким образом, чтобы разделить число 60 в отношении 2 : 3, можно разделить число 60 на сумму членов отношения 2 + 3 и результат умножить на каждый член отношения.

Задача 1. Два брата сложили свои деньги для покупки акций. Старший внес 500 р., а младший – 300 р. Через некоторое время они продали акции за 1000 р. Как они должны разделить эти деньги между собой?

Естественно разделить 100 р. в том отношении в котором они вложили деньги, т.е. в отношении 500 : 300 = 5 : 3.

1) старшему брату ;

2) младшему брату . Ответ : 625 р., 375 р.

Решить устно. После сбора урожая яблок одна их часть была высушена, а другая использована для приготовления сока. Сколько яблок пошло на сушку, а сколько на сок?

Подведение итогов урока. Как разделить число в данном отношении?

Домашнее задание. § 1.3 (выучить теорию); № 37(б,г), 40, 38.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Номер материала: ДБ-660190

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Студенты Хабаровского края перейдут на дистанционное обучение

Время чтения: 1 минута

Кабмин утвердил список вузов, в которых можно получить второе высшее образование бесплатно

Время чтения: 2 минуты

В Туве предложили ввести антиковидные паспорта для школьников

Время чтения: 2 минуты

Мишустин поручил проводить международную олимпиаду по философии

Время чтения: 0 минут

В школе в Пермском крае произошла стрельба

Время чтения: 1 минута

В Ульяновской области продлили школьные каникулы

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Деление числа в данном отношении

Урок 23. Математика 6 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Деление числа в данном отношении»

Представим себе такую историю…

– Саша, чем ты занимаешься? – поинтересовался у друга Паша.

– Хочу приготовить мороженое, – ответил Саша. – Уже и рецепт нашёл, и подготовил все ингредиенты, но вот только разобраться не могу, сколько чего брать.

– А что в рецепте написано? – уточнил Паша.

– В рецепте сказано, что для приготовления мороженого нужно смешать 3 части молока, 2 части сливок и 1 часть сахара, – прочитал Саша. – А как эти части высчитать, если я хочу приготовить, например, 3 килограмма мороженого?

– И вправду, сложная задача у тебя получается, – задумался Паша. – Как эти части считать, не понятно. Но я знаю, кто нам сможет помочь!

– Ребята, прежде чем я отвечу на ваш вопрос, давайте немного разомнёмся и выполним устные задания, – предложил Мудряш.

– Давайте сверимся! – сказал Мудряш. — Посмотрите, что у вас должно было получиться!

– Ну а теперь вернёмся к вашему вопросу, – начал Мудряш. – Чтобы ответить на вопрос «Сколько каких ингредиентов нужно взять для приготовления смеси мороженого?», прежде всего нужно научиться выполнять деление числа в данном отношении. Итак, вы хотите приготовить 3 килограмма мороженого. Для удобства давайте переведём килограммы в граммы, всё же так будет легче и привычнее считать.

– Так как 1 килограмм равен 1000 грамм, – стал размышлять Саша, – значит, я хочу приготовить 3000 грамм мороженого.

– Хорошо! – согласился Мудряш. – По рецепту для приготовления мороженого нужно смешать 3 части молока, 2 части сливок и 1 часть сахара. Будем считать, что смесь мороженого состоит из 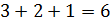частей, имеющих одинаковые массы. Тогда как посчитать, сколько приходится на 1 часть?

– Нужно 3000 разделить на 6, – ответил Паша.

– Правильно! – сказал Мудряш. – Значит, масса одной части смеси равна 500 граммам. По рецепту молоко в смеси составляет 3 части, сливки – 2 части, а сахар – 1 часть. Посчитайте, чему же будут равны эти части.

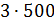
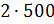
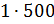
– Тогда масса молока в смеси будет равна и равна 1500 граммам, – принялся считать Саша. – Масса сливок будет равна и равна 1000 грамм, а масса сахара будет равна и равна 500 граммам.

– Получается, что для приготовления 3 килограммов мороженого нужно взять 1500 грамм молока, добавить 1000 грамм сливок, а затем добавить 500 грамм сахара? – решил уточнить Паша.

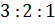
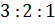
– Всё верно! – согласился Мудряш. – Из решения вашей задачи следует, что число 3000 можно представить в виде суммы трёх слагаемых – 1500, 1000 и 500, отношение которых равно . В таких случаях говорят, что число 3000 разделили в отношении . Также можно сказать, что число 3000 представили в виде суммы трёх слагаемых, пропорциональных числам 3, 2 и 1.

– И совсем несложная задача оказалась, – заметил Саша. – Теперь я без труда могу приготовить мороженое.

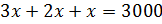
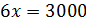
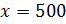
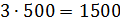
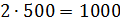
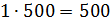
– Эту же задачу можно было решить и другим способом, – продолжил Мудряш. – Пусть масса одной части смеси мороженого составляет х грамм. Тогда массы молока, сливок и сахара составляют соответственно 3х грамм, 2х грамм и х грамм. Поскольку масса всей смеси мороженого равна 3000 грамм, то можем составить уравнение . Решим это уравнение. Получим, что . Отсюда . Тогда массы молока, сливок и сахара равны соответственно грамм, грамм и грамм.

– Сделаем вывод, – сказал Мудряш. – Чтобы разделить число в данном отношении, можно разделить это число на сумму членов отношения, а затем результат умножить на каждый член отношения.

– А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним несколько заданий.

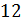
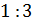
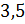
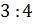
Задание первое: разделите числа в указанных отношениях: а) число в отношении ; б) число в отношении .

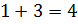
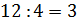
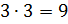
Решение: нужно разделить число 12 в отношении 1 к 3. Будем считать, что всё число состоит из частей. Значит, 1 часть равна . Тогда 3 части будут равны . Следовательно, число двенадцать можно разделить в отношении 1 к 3 так: 3 и 9.

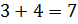
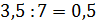
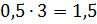
В следующем условии нам нужно разделить число 3,5 в отношении 3 к 4. Будем считать, что всё число состоит из частей. Тогда 1 часть равна . Отсюда 3 части числа равны . Следовательно, число 3,5 можно разделить в отношении 3 к 4 так: 1,5 и 2.

Следующее задание: два числа относятся как 4 к 7. Найдите эти числа, зная, что: их сумма равна 110, их разность равна 12.

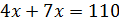
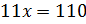
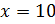
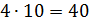
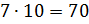
Решение: обозначим за х одну часть. Тогда можем записать, что первое число равно 4х, второе – 7х. В первом условии сказано, что сумма этих чисел равна 110. Составим уравнение . Решим его. Получим . Отсюда . Значит, первое число равно , второе – .

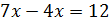
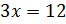
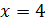
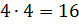
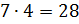
Во втором условии сказано, что разность этих чисел равна 12. Составим уравнение . Решим его. Получим . Отсюда . Значит, первое число равно , второе – .

Решим задачу: стороны прямоугольника 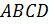относятся как 2 к 3. Найдите площадь этого прямоугольника, если его периметр равен 20 сантиметров.

И решим ещё одну задачу. Для приготовления фарфора смешивают 25 частей белой глины, 2 части песка и 1 часть гипса. Сколько нужно взять каждого материала, чтобы приготовить 504 грамма смеси?

Решение: будем считать, что вся смесь состоит из частей, имеющих одинаковые массы. Тогда 1 часть содержит грамм. Следовательно, чтобы приготовить 504 грамма смеси фарфора, нужно взять: грамм белой глины, грамм песка и грамм гипса.

Источник