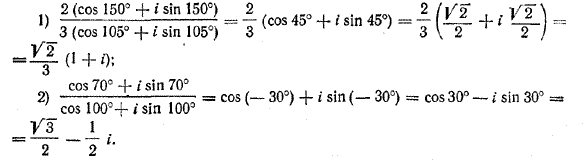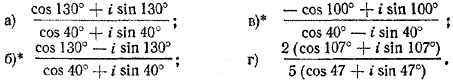деление комплексного числа в тригонометрической форме
Тригонометрическая форма комплексного числа
Рассмотрим комплексное число, заданной в обычной (алгебраической) форме:
Задача заключается в представлении комплексного числа (1) в тригонометрической форме. Для этого на комплексной плоскости введем полярные координаты. Примем за полюс начало координат, а за полярную ось вещественную ось R.
Как известно, полярными координатами точки z являются длина r ее радиус-вектора, равной расстоянию от точки z до полюса, и величина ее полярного угла, т.е. угла, образованного между полярной осью и вектором-радиусом точки z. Отметим, что направление отсчета угла берется от полярной оси до вектора-радиуса против часовой стрелки (Рис.1, Рис.2).
  |
На Рис.3 изображено комплексное число z. Координаты этого числа в декартовой системе координат (a, b). Из определения функций sin и cos любого угла, следует:
Подставляя (2) в (1), получим:
Эта форма записи называется тригонометрической формой записи комплексного числа.
Уравнения (2) возведем в квадрат и сложим:
  . . |
r−длина радиус-вектора комплексного числа z называется модулем комплексного числа и обозначается |z|. Очевидно |z|≥0, причем |z|=0 тогда и только тогда, когда z=0.
Величина полярного угла точки, соответвующей комплексному числу z, т.е. угла φ, называется аргументом этого числа и обозначается arg z. Заметим, что arg z имеет смысл лишь при z≠0. Аргумент комплексного числа 0 не имеет смысла.
Аргумент комплексного числа определен неоднозначно. Если φ аргумент комплексного числа, то φ+2πk, k=0,1. также является аргументом комплексного числа, т.к. cos(φ+2πk)=cosφ, sin(φ+2πk)=sinφ.
Приведение комплексного числа из алгебраической формы в тригонометрическую
Пусть комплексное число представлено в алгебраической форме: z=a+bi. Представим это число в тригонометрической форме. Вычисляем модуль комплексного числа: 


Пример 1. Представить комплексное число z=1 в тригонометрической форме.
Решение. Комплексное число z=1 можно представить так: z=1+0i. Вычислим модуль этого числа: 
Пример 2. Представить комплексное число z=i в тригонометрической форме.
Решение. Комплексное число z=i можно представить так: z=0+1i. Вычислим модуль этого числа: 

Ответ. 
Пример 3. Представить комплексное число z=4+3i в тригонометрической форме.
Решение. Вычислим модуль этого числа: 

Ответ. 
Умножение комплексных чисел в тригонометрической форме записи
В результате умножения комплексных чисел в тригонометрической форме мы получили комплексное число в тригонометрической форме, следовательно |z1z2|=r1r2, или
Пример 4. Умножить комплексные числа 

Решение. Воспользуемся формулой (5):
   |
Ответ. 
Деление комплексных чисел в тригонометрической форме записи
      |
Отсюда следует, что 
Далее 
Пример 5. Делить комплексные числа 

Решение. Воспользуемся формулой (8):
  |
Ответ. 
Правила деления комплексных чисел
Деление комплексных чисел — основные правила
Частным двух комплексных чисел \(z_<1>=a_<1>+b_ <1>i\) и \(z_<2>=a_<2>+b_ <2>\) i называют число z, заданное соотношением: \(z=\frac
Общий алгоритм для деления комплексных чисел на практике:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В каких формах это можно делать
Комплексные числа делят разными методами, подтвержденными доказательствами. Существуют алгебраическая, тригонометрическая и показательная формы для подобных операций. В каждом перечисленном случае необходимо использовать определенную формулу.
Формула деления в алгебраической форме
Когда требуется выполнить деление комплексных чисел в алгебраической форме, в первую очередь числитель и знаменатель умножают на число, сопряженное к знаменателю. Таким образом, удается исключить комплексность в знаменателе:
Формула деления в тригонометрической форме
Деление в тригонометрической форме подразумевает деление модулей комплексных чисел. После выполнения данной операции определяют разность аргументов:
Формула деления в показательной форме
Показательная форма деления комплексных чисел в тригонометрии предполагает деление модулей и вычисление разности аргументов в экспоненте:
Примеры решения задач
Необходимо найти частное пары комплексных чисел:
\(z_1 = 3+i\) и \(z_2 = 2-3i\)
Заметим, что комплексные числа заданы в алгебраической форме. В связи с этим целесообразно использовать в действиях соответствующую формулу.
Сопряженное комплексное число к знаменателю:
Нужно домножить и разделить на сопряженное комплексное число к знаменателю дроби. Таким образом, получится исключить комплексность в знаменателе:
Далее следует привести подобные слагаемые и записать вывод с ответом:
Требуется выполнить деление комплексных чисел:
Комплексные числа в условии задачи записаны в тригонометрической форме. По этой причине необходимо использовать в расчетах соответствующую формулу. В данном случае следует определить деление модулей и разность аргументов:
Следующим шагом является деление чисел:
Нужно найти частное комплексных чисел:
Решение: Согласно формуле деления в показательной форме определяем разность аргументов и частное модулей:
При подстановке в формулу полученных значений уравнение будет преобразовано следующим образом:
В первую очередь следует домножить числитель и знаменатель заданной дроби на число, комплексно сопряженное к знаменателю:
Данным числом является:
Затем следует перемножить комплексные числа, как алгебраические двучлены, с учетом:
Необходимо найти частное:
\(=2 \cdot\left[\cos \frac<\pi><2>+i \sin \frac<\pi><2>\right]=2 \cdot(0+i)=2 i\)
Необходимо разделить два комплексных числа:
С помощью соответствующей формулы можно записать уравнение:
Ответ: \( z_ <1>\div z_ <2>= 1+i\)
Необходимо вычислить частное комплексных чисел:
\(z_<1>=\sqrt <2>\left( \cos \frac<\pi> <2>+ i \sin \frac<\pi> <2>\right)\)
\(z_<2>=\sqrt <2>\left( \cos \frac<\pi> <4>+ i \sin \frac<\pi> <4>\right)\)
Используя соответствующую формулу, запишем:
\(z_ <1>\div z_ <2>= \frac
\(= 1 \cdot \left( \cos \frac<\pi> <4>+ i \sin \frac<\pi> <4>\right) = \cos \frac<\pi> <4>+ i \sin \frac<\pi><4>\)
Ответ: \( z_ <1>\div z_ <2>= \cos \frac<\pi> <4>+ i \sin \frac<\pi><4>\)
Требуется разделить два комплексных числа:
Используя соответствующую формулу деления комплексных чисел, можно решить уравнение:
Деление комплексного числа в тригонометрической форме
КОМПЛЕКСНЫЕ ЧИСЛА XI
§ 257. Умножение и деление комплексных чисел, заданных в тригонометрической форме
Умножение и деление комплексных чисел удобнее выполнять, если эти числа заданы в тригонометрической форме. Имеют место следующие теоремы.
Теорема 1. Модуль произведения двух комплексных чисел равен произведению их модулей, а аргумент — сумме их аргументов.
А это и означает, что модуль произведения z1 • z2 равен произведению модулей чисел z1 и z2, а аргумент произведения — сумме аргументов чисел z1 и z2. Теорема 1 доказана.
2 (cos 130° + i sin 130°) • 3 (cos 230° + i sin 230°) = 6 (cos 360° + i sin 360°) = 6.
5 (cos 47° + i sin 47°) • 4 (cos 13° + i sin 13°) = 20 (cos 60° + i sin 60°) =
Отметим, что доказанная теорема справедлива для любого числа сомножителей, то есть при любом п:
В частном случае, когда все сомножители равны между собой, получаем:
Эта формула носит название формулы Муавра*.
* М у а в р (1667—1754) — английский математик.
При r =1 она принимает вид:
Теорема 2. Модуль частного двух комплексных чисел равен частному модулей делимого и делителя; аргумент частного двух не равных нулю комплексных чисел равен разности аргументов делимого и делителя.
Производя умножение в левой части этого равенства, получаем:
Модули двух равных комплексных чисел, отличных от нуля, равны, а аргументы могут отличаться лишь на угол, кратный 2π. Поэтому из последнего равенства вытекает, что
где п — некоторое целое число.
Аргумент любого комплексного числа, отличного от нуля, определен лишь с точностью до угла, кратного 2π. Поэтому можно считать, что аргумент φ комплексного числа z равен
2056. Выполнить указанные действия:
а) 5 (cos 40° + i sin 40°) • 3 (cos 50° + i sin 50°);
б) 2 (cos 20° + i sin 20°) • 7 (cos 100° + i sin 100°);
2058. Как изменяется модуль и аргумент комплексного числа в результате умножения этого числа на:
2059. Выполнить деление:
2060. Как изменятся модуль и аргумент комплексного числа в результате деления этого числа на: a) i; б) — i?
Комплексные числа
 Алгебраическая форма записи комплексных чисел Алгебраическая форма записи комплексных чисел |
 Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме |
 Комплексно сопряженные числа Комплексно сопряженные числа |
 Модуль комплексного числа Модуль комплексного числа |
 Деление комплексных чисел, записанных в алгебраической форме Деление комплексных чисел, записанных в алгебраической форме |
 Изображение комплексных чисел радиус-векторами на координатной плоскости Изображение комплексных чисел радиус-векторами на координатной плоскости |
 Аргумент комплексного числа Аргумент комплексного числа |
 Тригонометрическая форма записи комплексного числа Тригонометрическая форма записи комплексного числа |
 Формула Эйлера. Экспоненциальная форма записи комплексного числа Формула Эйлера. Экспоненциальная форма записи комплексного числа |
 Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме |
 Извлечение корня натуральной степени из комплексного числа Извлечение корня натуральной степени из комплексного числа |
Алгебраическая форма записи комплексных чисел
Множеством комплексных чисел называют множество всевозможных пар (x, y) вещественных чисел, на котором определены операции сложения, вычитания и умножения по правилам, описанным чуть ниже.
Тригонометрическая и экспоненциальная формы записи комплексных чисел будут изложены чуть позже.
Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме
Комплексно сопряженные числа
 |  |
 |  |
 |  |
 |  |
 |  |
Модуль комплексного числа
Модулем комплексного числа z = x + i y называют вещественное число, обозначаемое | z | и определенное по формуле
Для произвольного комплексного числа z справедливо равенство:
а для произвольных комплексных чисел z1 и z2 справедливы неравенства:
 |  |
 |  |
 |  |
 |  |
Деление комплексных чисел, записанных в алгебраической форме
Деление комплексного числа z1 = x1 + i y1 на отличное от нуля комплексное число z2 = x2 + i y2 осуществляется по формуле
Используя обозначения модуля комплексного числа и комплексного сопряжения, частное от деления комплексных чисел можно представить в следующем виде:
Деление на нуль запрещено.
Изображение комплексных чисел радиус-векторами координатной плоскости
Рассмотрим плоскость с заданной на ней прямоугольной декартовой системой координат Oxy и напомним, что радиус-вектором на плоскости называют вектор, начало которого совпадает с началом системы координат.
При таком представлении комплексных чисел сумме комплексных чисел соответствует сумма радиус-векторов, а произведению комплексного числа на вещественное число соответствует произведение радиус–вектора на это число.
Аргумент комплексного числа
Считается, что комплексное число нуль аргумента не имеет.
Тогда оказывается справедливым равенство:
 | (3) |
 | (4) |
а аргумент определяется в соответствии со следующей Таблицей 1.
Для того, чтобы не загромождать запись, условимся, не оговаривая этого особо, символом k обозначать в Таблице 1 произвольное целое число.
Таблица 1. – Формулы для определения аргумента числа z = x + i y
| Расположение числа z | Знаки x и y | Главное значение аргумента | Аргумент | Примеры |
| Положительная вещественная полуось |  |  |  | |
| Положительная мнимая полуось |  |  |  | |
| Второй квадрант |  |  |  | |
| Отрицательная вещественная полуось | Положительная вещественная полуось | |||
| Знаки x и y | ||||
| Главное значение аргумента | 0 | |||
| Аргумент | φ = 2kπ | |||
| Примеры |  |
значение
аргумента



значение
аргумента



значение
аргумента



x z
квадрант
x z
мнимая
полуось
y z
квадрант
Положительная вещественная полуось
Главное значение аргумента:
Расположение числа z :
Главное значение аргумента:
Расположение числа z :
Положительная мнимая полуось
Главное значение аргумента:
Расположение числа z :
Главное значение аргумента:
Расположение числа z :
Отрицательная вещественная полуось
Отрицательная мнимая полуось
x z = x + i y может быть записано в виде
Формула Эйлера. Экспоненциальная форма записи комплексного числа
В курсе «Теория функций комплексного переменного», который студенты изучают в высших учебных заведениях, доказывается важная формула, называемая формулой Эйлера :
Из формулы Эйлера (6) и тригонометрической формы записи комплексного числа (5) вытекает, что любое отличное от нуля комплексное число z = x + i y может быть записано в виде
Из формулы (7) вытекают, в частности, следующие равенства:
а из формул (4) и (6) следует, что модуль комплексного числа
Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме
Экспоненциальная запись комплексного числа очень удобна для выполнения операций умножения, деления и возведения в натуральную степень комплексных чисел.
Действительно, умножение и деление двух произвольных комплексных чисел 

Таким образом, при перемножении комплексных чисел их модули перемножаются, а аргументы складываются.
При делении двух комплексных чисел модуль их частного равен частному их модулей, а аргумент частного равен разности аргументов делимого и делителя.
Возведение комплексного числа z = r e iφ в натуральную степень осуществляется по формуле
Другими словами, при возведении комплексного числа в степень, являющуюся натуральным числом, модуль числа возводится в эту степень, а аргумент умножается на показатель степени.
Извлечение корня натуральной степени из комплексного числа
Пусть 
Для того, чтобы решить уравнение (8), перепишем его в виде
следствием которых являются равенства
 | (9) |
Из формул (9) вытекает, что уравнение (8) имеет n различных корней
 | (10) |
то по формуле (10) получаем:
- деление квартиры в ипотеке при разводе с материнским капиталом
- деление комплексных чисел в алгебраической форме