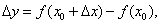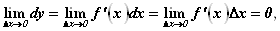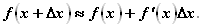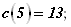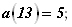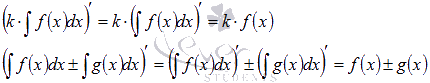дифференциал функции и его приложения

Что такое дифференциал функции?

Понятие дифференциала функции связано с такими важными математическими разделами как дифференциальное и интегральное исчисление и тесно связано с понятием производной функции. Наиболее часто дифференциал применяется для приближенных вычислений, а также для оценки погрешностей формул и измерений.

Дифференциал функции — это линейная часть приращения функции. Говоря о значении дифференциала функции, рассматривают конкретную точку функции и бесконечно малое изменение аргумента.

История открытия дифференциала

Чаще всего открытие дифференциально-интегрального исчисления принято связывать с именем Исаака Ньютона, однако, этот факт активно оспаривают учёные со всего света.

Действительно, открытие целого нового направления в науке, столь значимого для её развития, было бы ошибочно считать заслугой только одного учёного. Изначально интегрирование связывали с вычислением площадей и объёмов криволинейных фигур. Такие задачи, как известно, решались ещё во времена Архимеда, поэтому его имя также имеет отношение к открытию дифференциального исчисления.

Также дифференцирование имеет отношение к решению задач на проведение касательных к различным кривым. Данное направление активно развивали греческие математики. В те времена математики столкнулись с трудностью, которую не смогли решить в дальнейшем и представители Нового времени.

Дело в том, что для определения направления прямой требовалось знать координаты как минимум двух точек, а касательная имеет лишь одну точку соприкосновения с кривой. Этот факт натолкнул учёных на мысль о том, что в одной точке кривая может иметь несколько касательных. В то время ученые пришли к выводу, что прямая состоит не из точек, а из отрезков минимальной длины. Таким образом, они считали направление касательной в некоторой точке совпадающим с направлением атомарного отрезка в данной точке.

В дальнейшем учёные Нового времени опровергли данную теорию. В этот период огромный вклад в развитие науки внёс Исаак Ньютон. Ученый сформулировал определения и принципы решения производных, а также основы дифференциального исчисления, которых придерживаются учёные и в наши дни.

Дифференциальное исчисление широко применяется в математике и других науках для решения различных задач.

Геометрический смысл дифференциала

Геометрический смысл дифференциала заключается в следующем: дифференциал функции f(x) равен приращению ординаты касательной к графику функции, которая проведена через некоторую точку с координатами (x,y) при изменении координаты x на величину Δх=dx.

Дифференциал является главной линейной частью функции относительно приращения аргумента. Чем меньше приращение функции, тем большая доля приращения приходится на эту линейную часть.

Таким образом, при бесконечно малом Δх, приращение функции можно считать равным ее дифференциалу. Это свойство дифференциала позволяет использовать его для приблизительных вычислений и оценки погрешностей измерений.

Применение дифференциала в приближенных вычислениях

Поскольку дифференциал функции является частью ее приращения, то при бесконечно малом приращении аргумента он приблизительно равен приращению функции. При этом чем меньше приращение аргумента, тем точнее значение функции. Этот факт даёт возможность использования дифференциалов для приближённых вычислений.

С помощью таких вычислений можно решать различные виды задач. Приближённые вычисления практически всегда связаны с наличием погрешности.

Использование дифференциала для оценки погрешностей

Результаты измерений в большинстве случаев содержат ошибку, обусловленную неточностью измерительных приборов.

Число, несколько превышающее или равное этой неточности, называется «предельной абсолютной погрешностью».

Отношение предельной погрешности к значению измеряемой величины называют «предельной относительной погрешностью».

Для оценки величины погрешностей измерений используют дифференциальное исчисление.

Источник

Дифференциал функции, его геометрический смысл

Понятие и геометрический смысл дифференциала

Определение. Дифференциалом функции в некоторой точке x называется главная, линейная часть приращения функции.

Дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной x (аргумента).

Это записывается так:

Геометрический смысл дифференциала. Дифференциал функции y = f(x) равен приращению ординаты касательной S, проведённой к графику этой функции в точке M(x; y), при изменении x (аргумента) на величину (см. рисунок).

Почему дифференциал можно использовать в приближенных вычислениях?

Дифференциал, является главной, линейной относительно частью приращения функции; чем меньше , тем большую долю приращения составляет эта часть. В этом можно убедиться, мысленно передвигая перпендикуляр, опущенный из точки P (см. рисунок) к оси Ox, ближе к началу координат. Поэтому при малых значениях (и при ) приращение функции можно приближенно заменить его главной частью , т.е.

О разных формах записи дифференциала

Дифференциал функции в точке x и обозначают

(1)

, (2)

поскольку дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной.

Замечание. Нужно помнить, что если x – исходное значение аргумента, а 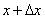— наращенное значение, то производная в выражении дифференциала берётся в исходной точке x ; в формуле (1) этого не видно из записи.

Дифференциал функции можно записать в другой форме:

(3)

(4)

В этом и следующем параграфах каждую из функций будем считать дифференцируемой при всех рассматриваемых значениях её аргументов.

Дифференциал обладает свойствами, аналогичными свойствам производной:

(С – постоянная величина) (5)

(6)

(7)

(8)

(9)

Формулы (5) – (9) получаются из соответствующих формул для производной умножением обеих частей каждого равенства на .

Применение дифференциала в приближенных вычислениях

Установленное во втором параграфе приближенное равенство

(10)

позволяет использовать дифференциал для приближенных вычислений значений функции.

Запишем приближенное равенство более подробно. Так как

(11)

Абсолютная и относительная погрешности приближенных вычислений

Пользуясь приближенным значением числа, нужно иметь возможность судить о степени его точности. С этой целью вычисляют его абсолютную и относительную погрешности.

Абсолютная погрешность приближенного числа равна абсолютной величине разности между точным числом и его приближенным значением:

(12)

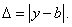
Относительной погрешностью приближенного числа называется отношение абсолютной погрешности этого числа к абсолютной величине соответствующего точного числа:

(13)

Если точное число неизвестно, то

(14)

Иногда, прежде чем применить формулу (11), требуется предварительно преобразовать исходную величину. Как правило, это делается в двух целях. Во-первых, надо добиться, чтобы величина была достаточно малой по сравнению с , так как чем меньше , тем точнее результат приближенного вычисления. Во-вторых, желательно, чтобы величина вычислялась просто.

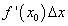
24.Приложение дифференциала функции к приближенным вычислениям

Применение дифференциала к приближенным вычислениям

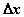
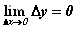
Понятие дифференциала подсказывает, что если какой-Либо процесс по характеру своего изменения близок к линейному, то приращение функции мало отличается от дифференциала. Кроме того, если функция имеет конечную производную в некоторой точке х, то ее приращение и дифференциал также бесконечно малы при , стремящемся к нулю:

,

Так как дифференцируемая функция непрерывна,

Потому что произведение ограниченной функции на бесконечно малую при DX, стремящемся к нулю, есть функция бесконечно малая.

Более того, эти две бесконечно малые функции при эквивалентны:

Эквивалентность и дает возможность при малых приращениях аргумента приближенно считать

Что может дать эта формула? Пусть в некоторой точке сравнительно просто вычисляются значения и . Тогда в другой точке , отстоящей недалеко от , возможно представление :

(11. 16)

Здесь остается открытым вопрос о точности получаемого результата. Это обстоятельство снижает ценность данной формулы приближенного вычисления, но в основном она полезна и широко применяется на практике.

Рассмотрим пример. В прямоугольном треугольнике катеты a=5 м и b=12 м. Какой будет гипотенуза этого треугольника, если катет a уменьшить на 0,2 м (рис. 11.5, a)?

Найдем первоначальную длину гипотенузы:

.

После уменьшения катета a на 0,2 м гипотенуза будет равна (рис. 11.5, a)

Применим теперь формулу (11.16) для приближенного нахождения с в связи с уменьшением катета a, рассматривая функцию вида:

(B=Const);

;

В обоих случаях мы получили приближенное значение искомой величины. Но в первом случае погрешность возникает в результате приближенных вычислений, а во втором, сравнительно более простом, – В связи с применением приближенной формулы (к ней также может добавиться погрешность, вызванная приближенными вычислениями). Отметим, что при уменьшении катета a На 0,2 м гипотенуза с уменьшилась примерно на 0,08 м, а полученные нами приближенные значения при этом отличаются лишь на 0,001 м.

Рассмотрим другую ситуацию: в этом же треугольнике уменьшим гипотенузу с на 0,2 м, оставив катет b без изменения (рис. 11.5, б). Определим, как в этом случае изменится катет A:

25.Приложение производной к исследованию функций и построению графика

Если на некотором промежутке график функции представляет собой непрерывную линию, иными словами, такую линию, которую можно провести без карандаша от листа бумаги, то такая функция называется непрерывной на этом промежутке. Существуют также функции, которые непрерывными не являются. В качестве примера рассмотрим график функции, которая на промежутках [a; c] и [с; b] непрерывна, но в точке
х = с разрывна и поэтому на всем отрезке [a; b] не является непрерывной. Все функции, изучаемые нами в школьном курсе математики, – это функции непрерывные на каждом промежутке, на котором они определены.

Отметим, что если на некотором промежутке функция имеет производную, то на этом промежутке она непрерывна.

Обратное утверждение является неверным. Функция, которая непрерывна на промежутке, может не иметь производной в некоторых точках этого промежутка. Например, функция
у = |log ₂ x| непрерывна на промежутке х > 0, но в точке х = 1 не имеет производной, в силу того что в этой точке график функции касательной не имеет.

Рассмотрим построение графиков с помощью производной.

Построить график функции f(x) = x 3 – 2x 2 + x.

1) Эта функция определена при всех х € R.

2) Найдем промежутки монотонности рассматриваемой функции и ее точки экстремума с помощью производной. Производная равна f ‘(x) = 3x 2 – 4x + 1. Найдем стационарные точки:
3x 2 – 4x + 1 = 0, откуда х₁ = 1/3, х₂ = 1.

Для определения знака производной разложим квадратные трехчлен 3x 2 – 4x + 1 на множители:
f ‘(x) = 3(х – 1/3)(х – 1). Следовательно, на промежутках х 1 производная положительна; значит, функция возрастает на этих промежутках.

Производная отрицательна при 1/3 3 – 2(1/3) 2 + 1/3 = 4/27.

Точкой минимума является точка х₂ = 1, так как слева от этой точки функция убывает, а справа возрастает; ее значение в этой точке минимума равняется f (1) = 0.

3) При построение графика обычно находят точки пересечения графика с осями координат. Так как f(0) = 0, то график проходит через начало координат. Решая уравнение f(0) = 0, находим точки пересечения графика с осью абсцисс:

x 3 – 2x 2 + x = 0, х(x 2 – 2х + 1) = 0, х(х – 1) 2 = 0, откуда х = 0, х = 1.

5) Используя результаты исследования (пункты 1 – 4), строим график функции у = x 3 – 2x 2 + x.

Для построения графика функции обычно сначала исследуют свойства этой функции с помощью ее производной по схеме, аналогичной схеме при решении задачи 1.

Таким образом, при исследовании свойств функции необходимо найти:

1) область ее определения;

3) стационарные точки;

4) промежутки возрастания и убывания;

5) точки экстремума и значения функции в этих точках.

Результаты исследования удобно записывать в виде таблицы. Затем, используя таблицу, строят график функции. Для более точного построения графика обычно находят точки его пересечения с осями координат и – при необходимости – еще несколько точек графика.

Для краткости решения задач на построение графиков функции большую часть рассуждений проводят устно.

Также отметим, что при решении некоторых задач мы можем столкнуться с необходимостью исследования функции не на всей области определения, а только на некотором промежутке, например, если нужно построить график, скажем, функции f(x) = 1 + 2x 2 – x 4 на отрезке [-1; 2].

26.Первообразная функции. Неопределенный интеграл и его свойства

Первообразной функции f(x) на промежутке (a; b) называется такая функция F(x), что выполняется равенство 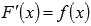для любого х из заданного промежутка.

Если принять во внимание тот факт, что производная от константы С равна нулю, то справедливо равенство . Таким образом, функция f(x) имеет множество первообразных F(x)+C, для произвольной константы С, причем эти первообразные отличаются друг от друга на произвольную постоянную величину.

Определение неопределенного интеграла.

Все множество первообразных функции f(x) называется неопределенным интегралом этой функции и обозначается .

Выражение называют подынтегральным выражением, а f(x) – подынтегральной функцией. Подынтегральное выражение представляет собой дифференциал функции f(x).

Действие нахождения неизвестной функции по заданному ее дифференциалу называетсянеопределенным интегрированием, потому что результатом интегрирования является не одна функция F(x), а множество ее первообразных F(x)+C.

На основании свойств производной можно сформулировать и доказать свойства неопределенного интеграла (свойства первообразной).

1.
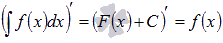
Производная результата интегрирования равна подынтегральной функции.

2.
Неопределенный интеграл дифференциала функции равен сумме самой функции и произвольной константы.

3. , где k – произвольная константа.
Коэффициент можно выносить за знак неопределенного интеграла.

4.
Неопределенный интеграл суммы/разности функций равен сумме/разности неопределенных интегралов функций.

Промежуточные равенства первого и второго свойств неопределенного интеграла приведены для пояснения.

Для доказательства третьего и четвертого свойств достаточно найти производные от правых частей равенств:

Эти производные равны подынтегральным функциям, что и является доказательством в силу первого свойства. Оно же используется в последних переходах.

Таким образом, задача интегрирования является обратной задаче дифференцирования, причем между этими задачами очень тесная связь:

· первое свойство позволяет проводить проверку интегрирования. Чтобы проверить правильность выполненного интегрирования достаточно вычислить производную полученного результата. Если полученная в результате дифференцирования функция окажется равной подынтегральной функции, то это будет означать, что интегрирование проведено верно;

· второе свойство неопределенного интеграла позволяет по известному дифференциалу функции найти ее первообразную. На этом свойстве основано непосредственное вычисление неопределенных интегралов.

Найти первообразную функции 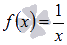, значение которой равно единице при х = 1.

Мы знаем из дифференциального исчисления, что 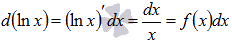(достаточно заглянуть в таблицу производных основных элементарных функций). Таким образом, . По второму свойству . То есть, имеем множество первообразных . При х = 1 получим значение . По условию, это значение должно быть равно единице, следовательно, С = 1. Искомая первообразная примет вид .

Если таблицу производных основных элементарных функций переписать в виде дифференциалов, то из нее по второму свойству неопределенного интеграла можно составить таблицу первообразных.

Источник