дифференциальная форма закона полного тока

Закон полного тока простыми словами

Какую зависимость устанавливает закон полного тока для магнитного поля. Формулировка закона простым языком и все необходимые формулы для расчета.

Знакомый многим предмет под названием «Электротехника» содержит в своей программе ряд основополагающих законов, определяющих принципы физического взаимодействия для магнитного поля. Они распространяют свое действие на различные элементы электротехнических устройств, а также на входящие в их состав структуры и среды. Физика происходящих в них процессов касается таких базовых понятий, как потоки электричества и поля. Закон полного тока устанавливает зависимость между перемещением электрических зарядов и создаваемым им магнитным полем (точнее – его напряженностью). Современная наука утверждает, что его применение распространяется практически на все среды.

Суть закона

Рассматриваемый закон, применимый в магнитных цепях, определяет следующую количественную связь между входящими в него составляющими. Циркуляция вектора магнитного поля по замкнутому контуру пропорциональна сумме токов, пронизывающих его. Чтобы понять физический смысл закона полного тока – потребуется ознакомиться с графическим представлением описываемых им процессов.

Из рисунка видно, что около двух проводников с протекающими по ним токами I1 и I2 образуется поле, ограниченное контуром L. Оно вводится как мысленно представляемая замкнутая фигура, плоскость которой пронизывают проводники с движущимися зарядами. Простыми словами этот закон можно выразить так. При наличии нескольких потоков электричества через мысленное представляемую поверхность, охватываемую контуром L, в ее пределах формируется магнитное поле с заданным распределением напряженности.

За положительное направление движения вектора в соответствии с законом для контура магнитной цепи выбирается ход часовой стрелки. Оно также является мысленно представляемым.

Такое определение создаваемого токами вихревого поля предполагает, что направление каждого из токов может быть произвольным.

Для справки! Вводимую полевую структуру и описывающий ее аппарат следует отличать от циркуляции электростатического вектора «Е», который при обходе контура всегда равен нулю. Вследствие этого такое поле относится к потенциальным структурам. Циркуляция же вектора «В» магнитного поля никогда не бывает нулевой. Именно поэтому оно называется «вихревым».

Основные понятия

В соответствии с рассматриваемым законом для расчета магнитных полей применяется следующий упрощенный подход. Полный ток представляется в виде суммы нескольких составляющих, протекающих через поверхность, охватываемую замкнутым контуром L. Теоретические выкладки могут быть представлены следующим образом:

Напряженность магнитного поля вдоль контура вычисляется на основании полученных выкладок по специальным методикам. Для ее нахождения придется проинтегрировать этот параметр по L, используя уравнение Максвелла, представленное в одной из форм.Оно может быть применено и в дифференциальной форме, но это несколько усложнит выкладки.

Влияние среды

Рассмотренные отношения для закона токов и полей, действующих не в вакууме, а в магнитной среде, приобретают несколько иной вид. В этом случае помимо основных токовых составляющих вводится понятие микроскопических токов, возникающих в магнетике, например, или в любом подобном ему материале.

Нужное соотношение в полном виде выводится из теоремы о векторной циркуляции магнитной индукции B. Простым языком она выражается в следующем виде. Суммарное значение вектора B при интегрировании по выбранному контуру равно сумме охватываемых им макро токов, умноженной на коэффициент магнитной постоянной.

В итоге формула для «В» в веществе определяется выражением:

Интеграл от B по dL = интегралу от Bl по dL= m(I+I1)

где: dL – дискретный элемент контура, направленный вдоль его обхода, Вl– составляющая в направлении касательной в произвольной точке,бI и I1 – ток проводимости и микроскопический (молекулярный) ток.

Если поле действует в среде, состоящей из произвольных материалов – должны учитываться микроскопические токи, характерные именно для этих структур.

Эти выкладки также верны для поля, создаваемого в соленоиде или в любой другой среде, обладающей конечной магнитной проницаемостью.

Для справки

В самой полной и объемлющей системе измерений СГС напряженность магнитного поля представляется в эрстедах (Э). В другой действующей системе (СИ) она выражается в амперах на один метр (А/метр). Сегодня эрстед постепенно вытесняется более удобной в работе единицей – ампером на метр. При переводе результатов измерений или расчетов из СИ в СГС используется следующее соотношение:

1 Э = 1000/(4π) А/м ≈ 79,5775 Ампер/метр.

В заключительной части обзора отметим, что независимо от того, какая используется формулировка закона полных токов – суть его остается неизменной. Своими словами это можно представить так: он выражает отношения между токами, пронизывающими данный контур и создаваемыми в веществе магнитными полями.

Напоследок рекомендуем просмотреть полезное видео по теме статьи:

Источник

Закон полного тока в дифференциальной форме

Основным законом, характеризующим свойства магнитного поля, является закон полного тока, который устанавливает связь между напряженностью магнитного поля и током. Он гласит: циркуляция вектора напряженности магнитного поля вдоль замкнутого контура равна алгебраической сумме токов, сцепленных с этим контуром:

.

Положительное направление тока связано с направлением обхода контура правилом правого винта. Если обозначить плотность тока 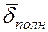, то ток, проходящий через поверхность S, ограниченную кривой L,

.

Пользуясь теоремой Стокса можно записать равенство

Так как это равенство справедливо для всех значений предела интегрирования S, то подинтегральные функции равны между собой:

.

(43.5)

Формула (43.5) представляет собой закон полного тока в дифференциальной форме и носит название первого уравнения Максвелла. Оно указывает на то, что магнитное поле является полем вихревым.

Ротор – это функция, характеризующая поле в рассматриваемой точке в отношении способности к образованию вихрей.

Вихревыми принято называть поля, в которых ротор векторной величины, описывающей поле, отличен от нуля. Так как для магнитного поля постоянного тока 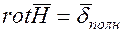, то во всех точках пространства, где , поле вектора является вихревым.

В тех же точках пространства, где , и соответственно , магнитное поле можно рассматривать как потенциальное.

3. Раскрытие выражения rot 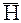= в декартовой системе

Координат

В декартовой системе координатrot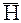раскрывается следующим образом:

(43.6)

4. Раскрытие rot = в виде определителя в декартовой

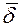
Системе

Ротор любого вектора, используемого в теории электромагнитного поля, можно представить в виде определителя третьего порядка. Так, rot в декартовой системе записывают в виде следующего определителя:

rot = .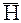

(43.7)

Принцип непрерывности магнитного потока

Под магнитным потоком понимают поток вектора магнитной индукции через некоторую поверхность:

.

(43.8)

Магнитный поток измеряется в веберах (вб).

Магнитную индукцию можно определить как плотность магнитного потока. Если площадь S перпендикулярна вектору и поле однородное, то

Установлено, что магнитный поток сквозь замкнутую поверхность всегда равен нулю:

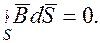(43.9)

Пользуясь теоремой Остроградского, можно записать:

Так как это равенство справедливо для любого объема, то

(43.10)

Последняя формула выражает принцип непрерывности магнитного потока в дифференциальной форме. Она означает, что линии магнитной индукции не имеют ни истоков, ни стоков и являются замкнутыми сами на себя линиями.

Источник

Дифференциальная форма закона полного тока

Соотношение (13.3) пригодно для контура любых размеров, в том числе и для весьма малого. Выделим в какой-либо среде небольшой контур («жирно» обведен на рис. 13.3) и составим вдоль него циркуляцию вектора Н. Циркуляция напряженности поля вдоль этого контура равна току, пронизывающему обведенную площадь. Если площадь мала, то можно полагать, что плотность тока d в пределах этой площади одинакова и тогда ток, пронизывающий площадь, Di = dDS = d_nDS. Здесь d_n — проекция вектора плотности тока d на нормаль к площади, т. е. на направление DS; .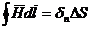

За положительное направление нормали к площади принимают направление движения острия правого винта, головка которого вращается в направлении, принятом за поло­жительное при обходе контура и составлении циркуляции.

Рис. 13.3. Иллюстрация к дифференциальному закону полного тока.

Разделим обе части равенства на DS и устремим DS к нулю. Это будет соответствовать стягиванию рассматриваемой площади к нулю. Предел полученного отношения

.

В левой части равенства находится величина, которая является проекцией ротора Н на направление нормали к площади DS. Следовательно, rot_n Н = d_n. Если площадь DS ориентировать в пространстве так, что направление нормали к ней совпадет с направлением вектора плотности тока d в данной точке поля, то тогда вместо равенства проекций двух векторов (rot_nН и d_n) можно записать равенство самих векторов

rot Н = d.(13.4)

Формула (13.4) и представляет собой закон полного тока в дифференциальной форме.

Ротор — это функция, характеризующая поле в рассматриваемой точке в отношении способности к образованию вихрей.

Уравнение (13.4) записано в общей форме, безотносительно к системе координат, и в каждой конкретной системе координат оно раскрывается по-своему.

13.4. Раскрытие выражения rot Н= d в декартовой системе координат

Равенство двух векторов rot Н и dозначает, что равны проекции их на ось х, проекции на ось у и проекции на ось z. Проекция rotН на ось z равна , проекция вектора d на ось z есть d_z и т. д.

На рис. 13.4 в декартовой системе координат изображен малый прямоугольный контур mnpq. Обойдем этот контур против часовой стрелки и составим циркуляцию вектора Н; при ее составлении необходимо учесть изменение вектора Hот точки к точке. Обозначим проекции Н на оси х и у в точке m соответственно через Н_x и H_y.

В точке n проекция на ось x изменится по сравнению с проекцией в точке m и будет равной ; проекцией на ось y будет . В точке q и . В точке p + и .

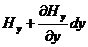
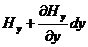
При составлении циркуляции на участках mn и рq необходимо принимать во внимание лишь «иксовые» составляющие Н( «игрековые» составляющие перпендикулярны элементу пути ).

Составляющую на участке mn находят как произведение среднего значения «иксовой» составляющей напряженности на этом участке на длину пути dx

,

на участке np ,

на участке pq ,

на участке qm .

Рис. 13.4. Раскрытие выражения rot H = d в декартовой системе координат.

Если просуммировать все составляющие циркуляции вдоль кон­тура mnpq, то получим:

.

В соответствии с определением проекции ротора на ось z разделим циркуляцию на площадь dS_z = dxdy, после чего проекция ротора на направление оси z:

.

и .

.(13.5)

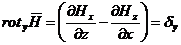
Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.

Источник

Дифференциальная форма закона полного тока

Дифференциальная форма закона полного тока

Дифференциальная форма закона полного тока. Соотношение (15.3) подходит для контуров любого размера, включая очень маленькие контуры. Для некоторых носителей выбран маленький контур (выделен жирным шрифтом на рисунке 442), и циркуляция секторов настроена соответствующим образом.

плотность тока 6 на этом площадки одинакова и токи через площадку равны. Людмила Фирмаль

Где bl — проекция текущего вектора нормали b в направлении As, то есть нормали сайта-> сайт. // dl = 6 нАс. Для положительного направления нормального участка берется направление движения правого наконечника винта, и головка вращается в положительном направлении при обходе цепи во время круговой компиляции.

Разделите обе части равенства на As и укажите As на ноль. Это соответствует сокращению «жирный», обведенное на рисунке. Обнулить 442 сайта. Предел полученного отношения равен (£ 7 / dT lim = 6, j. As-> 0.

Следовательно, rot „tf = 6″. Область As указывает в направлении пространства, а направлением нормали является плотность тока. Если оно совпадает с направлением вектора-> плотности тока в конкретной точке поля b, то (rotn 77 и ёl), уравнение t самого вектора, то есть rot H = 7. (15.4)

можно записать проекционное уравнение двух векторов Людмила Фирмаль

Последнее уравнение является дифференциальной формой закона полного тока, которое часто используется при расчете магнитного поля и может быть определено как функция, которая характеризует поле в данной точке с точки зрения его способности к образованию.

(15.4) записывается в общем формате независимо от системы координат и определяется уникальным образом для каждой конкретной системы координат. Это будет сделано.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Закон полного тока для магнитного поля

В электрических цепях всегда присутствует магнитное поле, которое оказывает электромагнитное взаимодействие с токами этих цепей. Данный фактор учитывается при расчетах цепей, а закон полного тока для магнитного поля является инструментом для подобных вычислений.

Если поднести магнитную стрелку к проводнику, по которому течёт ток, её положение изменится. Это говорит о наличии вокруг проводника кроме электрического ещё и магнитного поля. В результате многочисленных исследований электромагнитных явлений установлено, что существует взаимное влияние полей, имеющих электрическую и магнитную природу.

Физический смысл закона

Рассмотрим упрощённый вариант влияния магнитной индукции на электрическое поле. Для этого представим себе два параллельных проводника, по которым циркулируют постоянные токи, например, I₁ и I₂. Вблизи этих проводников образуется поле, которое мысленно можно ограничить неким контуром L – воображаемой замкнутой фигурой, плоскость которой пересекает потоки движущихся зарядов.

В пределах плоскости, охватываемой контуром L, формируется магнитное поле, напряжённость которого распределена в соответствии с направлениями токов. При этом циркуляция вектора магнитного поля в плоскости замкнутого контура прямо пропорциональна сумме токов, пронзающих данный контур. Полный электрический ток равен векторной сумме его составляющих:

Направления векторов I₁ и I₂ определяется по правилу буравчика.

Приведённые выше рассуждения можно рассматривать в качестве примера изображающего упрощённую модель частного случая рассматриваемого закона. В действительности же, процессы взаимного влияния магнитных и электрических полей намного сложнее, и они описываются интегральными и дифференциальными уравнениями Максвелла.

Упрощенный подход

Выразить закон в дифференциальном представлении довольно сложно. Потребуется вводить дополнительные компоненты. Необходимо учитывать влияние молекулярных токов. Наличие вихревых токов является причиной образования магнитного вихревого поля в пределах контура.

Вектор электрического смещения сравним с вектором напряжённости присутствующего магнитного поля H. При этом Ориентация вектора смещения зависит от быстроты изменения магнитной индукции.

Для упрощения вычислений на практике часто пользуются формулами закона для магнитного поля полных токов, представленных в виде суммирования предельно малых участков контура, с учётом влияния вихревых полей. При реализации этого метода контур мысленно разбивают на бесконечно малые отрезки. На этих отрезках проводники считаются прямолинейными, а магнитное поле на таких участках контура считают однородным.

На одном дискретном участке вектор напряженности U_m определяется по формуле: U_m= H_L×ΔL, где H_L– циркуляция вектора напряжённости на участке ΔL контура L. Тогда суммарная напряжённость U_L вдоль всего контура вычисляется по формуле: U_L= Σ H_L× ΔL.

Закон в интегральном представлении

Рассмотрим бесконечно прямой проводник, по которому циркулирует электрический ток, образующий поле, ограниченное контуром в виде окружности. Плоскость, пронизывающая проводник, – это круг, очерчённый линией данной окружности (см. рис. 1).

Рис. 1. Поле бесконечно прямого тока

Воспользуемся методом разбиения контура на мизерные участки dl (элементарные векторы длины контура). Пусть φ – угол между векторами dl и B. В нашем случае, при суммировании отрезков, вектор индукции B поворачивается так, что он очерчивает круг, то есть угол φ → 2π.

Из теоремы Остроградского-Гаусса вытекает формула:

Учитывая, что cos φ = 1,

Данная формула – постулат, подтверждённый экспериментально. Согласно этому постулату, циркуляция вектора B по окружности, то есть по замкнутому контуру, равна μ₀I, где μ₀ = 1/c 2 ε₀ – магнитная постоянная.

Ориентация вектора dB определяется путём применения правила буравчика. Это направление всегда перпендикулярно вектору плотности. Если проводников будет несколько (например, N), тогда

Каждый ток, с учётом знака, необходимо учитывать такое количество раз, которое соответствует числу его охватов контуром.

Ток берётся со знаком «+», если он по направлению обхода образует правовинтовую систему. При этом, отрицательным считается ток противоположного направления.

Заметим, что формула справедлива только для вакуума. В обычных условиях необходимо учитывать проницаемость среды.

Если ток распределён в пространстве (произвольный ток), тогда

где S – натянутая на контур поверхность, j – объёмная плотность тока. С учётом последнего выражения, формулу полного тока в вакууме можно записать:

Рис. 2. Иллюстрация закона для вакуума

Влияние среды

На результат взаимодействия магнитных потоков и постоянных токов влияет среда. Вещества обладают магнитной проницаемостью в потоке вектора индукции, что вносит коррективы на взаимодействие магнитной среды с токами проводимости. В однородной изотопной среде, где значение вектора электромагнитной индукции одинаково во всех точках, векторы B и H связаны между собой следующим соотношением:

где H — напряжённость магнитного поля, символом μ обозначена магнитная проницаемость.

Носители электрических зарядов создают собственные микротоки. Циркуляция вектора, характеризующего электростатическое поле, всегда нулевая. Поэтому электростатические поля, в отличие от магнитных, являются потенциальными.

Вектор B отображает результирующее значение полей макро- и микротоков. Линии электростатической индукции всегда остаются замкнутыми, в том числе и на положительных зарядах.

Рис. 3. Закон полного тока в веществе

Для полей, которые действуют в среде, состоящей из разных веществ, необходимо учитывать микротоки, характерные именно для конкретных структур, образующих данную среду.

Утверждение, изложенное выше, верно для полей соленоидов или любой другой структуры, обладающей свойствами конечной магнитной проницаемости.

Торойд

В электротехнике часто приходится иметь дело с катушками разных видов и размеров. Катушка, образованная витками намотанными на сердечник тороидальной формы (в виде бублика), называется тороидом. Важными характеристиками сердечника тора являются его радиусы — внутренний (R₁) и внешний (R₂).

Поле внутри соленоида на расстоянии r от центра равно:

Выводы

На основании изложенного, приходим к заключению:

При вычислениях не имеет значения, какую формулу мы используем – суть закона остаётся неизменной: он выражает взаимодействия, которые происходят между токами и создаваемыми ими магнитными полями, пронизывающими замкнутый контур.

Выводы закона учитываются при конструировании электромагнитных устройств. Наличие завихрений в электромагнитных полях приводит к снижению КПД. Кроме того, вихревые поля негативно влияют на работоспособность электронных элементов, расположенных в зоне их действий.

Конструкторы электротехнических приборов стремятся свести к минимуму таких влияний. Например, вместо обычных соленоидов применяют тороидальные катушки, за пределами которых отсутствуют электромагнитные поля.

Источник