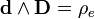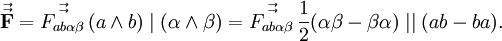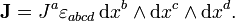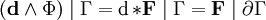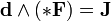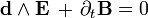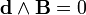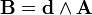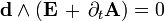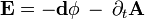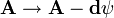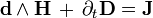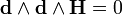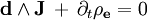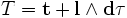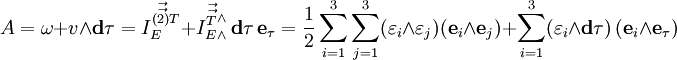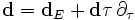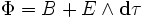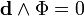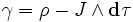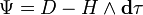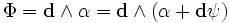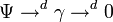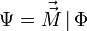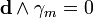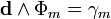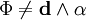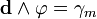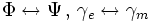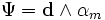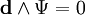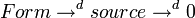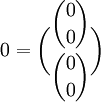дифференциальные формы в электродинамике

Дифференциальные формы в электромагнетизме

Дифференциальные формы в электромагнетизме — одна из возможных математических формулировок классической электродинамики при помощи дифференциальных форм.

Эта форма является формой кривизны тривиального главного расслоения со структурной группой U(1), с помощью которого могут быть описаны классическая электродинамика и калибровочная теория. 3-форма тока имеет вид

В этих обозначениях уравнения Максвелла могут быть очень компактно записаны как

где — оператор звезды Ходжа. Подобным образом может быть описана геометрия общей калибровочной теории.

2-форма также называется 2-формой Максвелла.

Литература

См. также

Полезное

Смотреть что такое «Дифференциальные формы в электромагнетизме» в других словарях:

Дифференциальные формы в электродинамике — Дифференциальные формы в электромагнетизме Содержание 1 Граф Десшампа 2 Дифференциальные формы в электродинамике … Википедия

Дифференциальная форма — порядка или форма кососимметрическое тензорное поле типа на касательном расслоении многообразия. Дифференциальные формы были введены Эли Картаном в начале XX века. Формализм дифференциальных форм оказывается удобен во многих разделах… … Википедия

Уравнения Максвелла — Классическая электродинамика … Википедия

Ковариантный метод — подход в теоретической физике, разработанный Ф. И. Фёдоровым на основе линейной алгебры и прямого тензорного исчисления. Получил распространение в приложении к описанию оптических явлений и, частично, в физике элементарных частиц. Содержание 1… … Википедия

Исчисление — У этого термина существуют и другие значения, см. Исчисление (значения) … Википедия

Источник

Дифференциальные формы в электромагнетизме

Дифференциальные формы в электромагнетизме

Содержание

Граф Десшампа [ править | править код ]

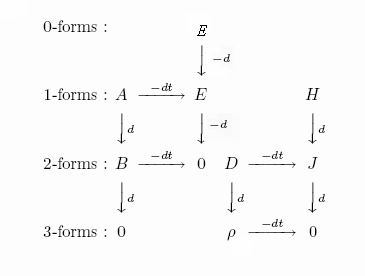
Уравнения Максвелла-Фарадея и Максвелла-Ампера с использованием дифференциальных форм в трёх измерениях, следуя Десшампу, можно изобразить в виде графа

где Undefined control sequence \bold \bold \wedge обозначает внешнее дифференцирование формы по метрическому пространству, а Undefined control sequence \bold \boldt — дифференцирование формы по времени. Знак минус обозначает, что дифференциал суммируется с обратным знаком.

Для получения выражений, надо просуммировать (с учётом знака) все входящие стрелки (то-есть, соответствующие им дифференциалы) выбранной физической величины.

Дифференциальные формы в электродинамике [ править | править код ]

В этих обозначениях уравнения Максвелла в геометрических единицах могут быть очень компактно записаны как Undefined control sequence \bold \bold\wedge <\textbf> = \textbf <0>Undefined control sequence \bold \bold \wedge (<*\textbf>) = \textbf

где ∗ * — оператор Ходжа (он же звёздочка Ходжа или просто звёздочка). Подобным образом может быть описана геометрическая структура любой калибровочной теории.

Уравнение Максвелла-Ампера Undefined control sequence \bold \bold d \wedge \Psi = \gamma_e

Обобщённый граф уравнений Максвелла для дифференциальных форм в трёхмерном пространстве [ править | править код ]

Вторая половина так называемых уравнений Максвелла (впрочем сформулированных в таком виде Хевисайдом) называется уравнения Максвелла-Ампера. Вектор H заменяем на 1-форму H. Вектор D на 2-форму D. Тогда в нотации дифференциальных форм: Undefined control sequence \bold \bold \wedge \bold\, + \, \partial_t \mathbf = \mathbf и уравнение для 3-формы: Undefined control sequence \bold \bold \wedge \bold = \rho_e В правых частях этих выражений находятся плотности. J 2-форма плотности электрического тока или плотность магнитного потенциала. Undefined control sequence \bold \bold <\rho_e>3-форма плотность заряда или плотность кванта электрического поля. Применим операцию внешнего произведения по пространственной физической величине к уравнению для 2-формы. Тогда с учётом Undefined control sequence \bold \bold \wedge \bold \wedge \bold = 0 получим уравнение непрерывности: Undefined control sequence \bold \bold \wedge \bold\, + \, \partial_t \mathbf <\rho_e>= 0 Все выражения которые приведены выше можно представить в виде графа Десшампа (который приведён выше).

Обобщённый граф уравнений Максвелла для дифференциальных форм в четырёхмерном пространстве-времени [ править | править код ]

Запишем 2-форму для магнитного поля Undefined control sequence \bold \Phi = B + E \wedge \bold d \tau Тогда уравнения Максвелла-Фарадея сведутся в одно выражение: Undefined control sequence \bold \bold d \wedge \Phi = 0

Приведём граф Десшампа для четырёхмерного пространства-времени. α → d Φ → d 0 \alpha \to^d \Phi \to^d 0 Ψ → d γ → d 0 \Psi \to^d \gamma \to^d 0

Магнитные источники [ править | править код ]

В случае электрических и магнитных источников имеем: Undefined control sequence \bold \bold d \wedge \Psi = \gamma_e Undefined control sequence \bold \bold d \wedge \varphi = \gamma_m

И соответственно: Undefined control sequence \bold \bold d \wedge \Psi = 0

Выражения для суперформ [ править | править код ]

История [ править | править код ]

В статье 1981 года Десшамп [2] помещает два графа (DAG) для электромагнитных дифференциальных форм и описание аппарата дифференциальных форм. Оба графа взаимосвязи дифференциальных форм Дешампа полностью содержится в Системе Физических Величин Плотникова Н. А. Теоремы Стокса и Гаусса, а так же операции с дифференциальными формами различного порядка так же описаны в публикации Плотникова Н. А. от 1978 года.

В 2004 году Ismo V. Lindell [3] публикует книгу с подробным описанием аппарата дифференциальных форм и его применения к теории электромагнитного поля. Эта работа — отличное и глубокое введение в современный язык теории электромагнитного поля. Книга Ismo V. Lindell содержит последние результаты автора по исследованию сред со сложными электромагнитными свойствами. Ismo V. Lindell значительно развил аппарат математического описания физических процессов электромагнитного поля.

Источник

Дифференциальные формы в электродинамике

Дифференциальные формы в электромагнетизме

Содержание

Граф Десшампа

Уравнения Максвелла-Фарадея и Максвелла-Ампера с использованием дифференциальных форм в трёх измерениях, следуя Десшампу, можно изобразить в виде графа

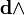
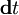
где обозначает внешнее дифференцирование формы по метрическому пространству, а — дифференцирование формы по времени. Знак минус обозначает, что дифференциал суммируется с обратным знаком.

Например, уравнения Максвелла — Ампера (сформулированные впервые Хевисайдом) можно получить из правого графа Десшампа, если записать выражения для J и D.

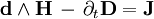
Для получения выражений, надо просуммировать (с учётом знака) все входящие стрелки (то-есть, соответствующие им дифференциалы) выбранной физической величины.

Дифференциальные формы в электродинамике

Максвелловская электродинамика весьма изящно формулируется на языке дифференциальных форм. Рассмотрим 2-форму Фарадея, соответствующую тензору электромагнитного поля:

Эта форма является формой кривизны тривиального главного расслоения со структурной группой U(1), аналогичная ситуация — лишь с другой группой — возникает в любой калибровочной теории. 3-форма тока имеет вид

или, что тоже самое (это выражение является обобщением теоремы Гаусса и теоремы Стокса):

В этих обозначениях уравнения Максвелла в геометрических единицах могут быть очень компактно записаны как

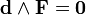
где * — оператор Ходжа (он же звёздочка Ходжа или просто звёздочка). Подобным образом может быть описана геометрическая структура любой калибровочной теории.

2-форма 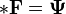также называется 2-формой Максвелла.

Обобщённый граф уравнений Максвелла для дифференциальных форм в трёхмерном пространстве

Запишем уравнения Максвелла в терминах дифференциальных форм для трёхмерного пространства. В дополнительной горизонтальной графе 2 показаны номера дифференциальных форм для трёхмерного пространства. Первая половина системы уравнений Максвелла называется уравнения Максвелла-Фарадея. При записи уравнений с использованием дифференциальных форм векторный оператор набла заменяется на операцию внешнего произведения по пространству. Для 1-формы E, которая представлена векторной физической величиной, эта операция есть . Для 2-формы В та же самая операция является . Получается уравнение для 2-формы:

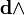
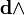
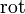
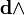
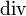
Все физические величины записаны в единицах системы СИ. Из теорема де Рама|теоремы де Рама следует: 2-форма В локально может быть представлена через 1-форму A:

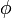
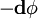
Используя снова теорему де Рама, мы определяем скалярный потенциал электрического поля 0-форму . Приравниваем выражение в скобках в последней формуле и напряжённость электрического поля, следовательно есть:

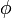
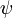
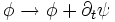
Представление полей в терминах векторного магнитного потенциала и скалярного электрического потенциала неоднозначно, так как потенциалы A и могут отличаться на любую скалярную функцию .

,

Такое условие называется условием Лоренца. Эти уравнения не зависят от природы электромагнитной среды.

Вторая половина так называемых уравнений Максвелла (впрочем сформулированных в таком виде Хевисайдом) называется уравнения Максвелла-Ампера. Вектор H заменяем на 1-форму H. Вектор D на 2-форму D. Тогда в нотации дифференциальных форм:

В правых частях этих выражений находятся плотности. J 2-форма плотности электрического тока или плотность магнитного потенциала. 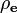3-форма плотность заряда или плотность кванта электрического поля. Применим операцию внешнего произведения по пространственной физической величине к уравнению для 2-формы. Тогда с учётом

Все выражения которые приведены выше можно представить в виде графа Десшампа (который приведён выше).

Обобщённый граф уравнений Максвелла для дифференциальных форм в четырёхмерном пространстве-времени

Запишем 1-форму для четырёхмерного времени-пространства.

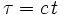
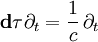
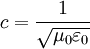
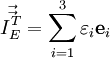
Запишем дифференциальный оператор Минковского для четырёхмерного пространства (пространство-время).

.

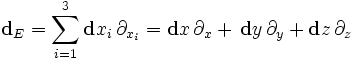
Тогда уравнения Максвелла-Фарадея сведутся в одно выражение:

Запишем 3-форму источников для уравненений Максвелла-Ампера

Запишем 1-форму 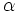для четырёхмерного потенциала электромагнитного поля (используем теорему де Рама, лемму Пуанкаре).

где 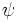0-форма или скалярная функция.

Приведём граф Десшампа для четырёхмерного пространства-времени.

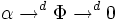
Запишем материальное уравнение для среды.

где 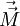— двухэлементный тензор(diadics).

Магнитные источники

Магнитный источник состоит из четырёхмерной 2-формы магнитного тока J_m и четырёхмерной 3-формы плотности магнитного заряда ρ_m :

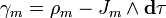
По теореме де Рама магнитный четыре ток можно представить через вторую форму:

При постоянных магнитных источниках не может быть выражена через 1-форму для четырёхмерного потенциала электромагнитного поля (используем теорему де Рама, лемму Пуанкаре):

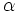
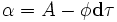
В случае электрических и магнитных источников имеем:

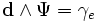
Или что тоже самое:

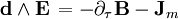
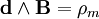
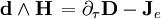
Четыре 2-Формы и Четыре источники (3-формы) взаимно заменяемы (можно трансформировать одно в другое):

При исчезающих электрических источниках ( γ_e = 0 ) Ψ может быть выажена через магнитный четыре потенциал:

Выражения для суперформ

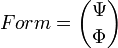
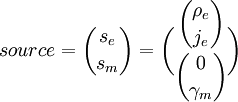
История

В статье 1981 года Десшамп [2] помещает два графа (DAG) для электромагнитных дифференциальных форм и описание аппарата дифференциальных форм. Оба графа взаимосвязи дифференциальных форм Дешампа полностью содержится в Системе Физических Величин Плотникова Н. А. Теоремы Стокса и Гаусса, а так же операции с дифференциальными формами различного порядка так же описаны в публикации Плотникова Н. А. от 1978 года.

В 2004 году Ismo V. Lindell [3] публикует книгу с подробным описанием аппарата дифференциальных форм и его применения к теории электромагнитного поля. Эта работа — отличное и глубокое введение в современный язык теории электромагнитного поля. Книга Ismo V. Lindell содержит последние результаты автора по исследованию сред со сложными электромагнитными свойствами. Ismo V. Lindell значительно развил аппарат математического описания физических процессов электромагнитного поля.

Примечания

Литература

См. также

Полезное

Смотреть что такое «Дифференциальные формы в электродинамике» в других словарях:

Дифференциальная форма — порядка или форма кососимметрическое тензорное поле типа на касательном расслоении многообразия. Дифференциальные формы были введены Эли Картаном в начале XX века. Формализм дифференциальных форм оказывается удобен во многих разделах… … Википедия

Внешний дифференциал — Дифференциальная форма порядка k или k форма кососимметрическое тензорное поле типа на касательном расслоении многообразия. Дифференциальные формы были введены Картаном в начале XX века. Формализм дифференциальных форм оказывается удобен во… … Википедия

Внешняя производная — Дифференциальная форма порядка k или k форма кососимметрическое тензорное поле типа на касательном расслоении многообразия. Дифференциальные формы были введены Картаном в начале XX века. Формализм дифференциальных форм оказывается удобен во… … Википедия

Внутренняя производная — Дифференциальная форма порядка k или k форма кососимметрическое тензорное поле типа на касательном расслоении многообразия. Дифференциальные формы были введены Картаном в начале XX века. Формализм дифференциальных форм оказывается удобен во… … Википедия

Замкнутая форма — Дифференциальная форма порядка k или k форма кососимметрическое тензорное поле типа на касательном расслоении многообразия. Дифференциальные формы были введены Картаном в начале XX века. Формализм дифференциальных форм оказывается удобен во… … Википедия

Ковектор — Дифференциальная форма порядка k или k форма кососимметрическое тензорное поле типа на касательном расслоении многообразия. Дифференциальные формы были введены Картаном в начале XX века. Формализм дифференциальных форм оказывается удобен во… … Википедия

Уравнения Максвелла — Классическая электродинамика … Википедия

Вариационные принципы — Принципами механики называются исходные положения, отражающие столь общие закономерности механических явлений, что из них как следствия можно получить все уравнения, определяющие движение механической системы (или условия её равновесия). В ходе… … Википедия

Вариационные принципы механики — Принципами механики называются исходные положения, отражающие столь общие закономерности механических явлений, что из них как следствия можно получить все уравнения, определяющие движение механической системы (или условия её равновесия).… … Большая советская энциклопедия

ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ — Принципами механики наз. исходные положения, отражающие столь общие закономерности механич. явлений, что из этих положений как следствия можно получить ур ния, определяющие движения механич. системы (или условия её равновесия). В механике… … Физическая энциклопедия

Источник