для определения параметров структурную форму модели необходимо преобразовать в

Системы эконометрических уравнений

1. Наибольшее распространение в эконометрических исследованиях получили:

в) системы взаимозависимых уравнений.

2. Эндогенные переменные – это:

б) зависимые переменные, число которых равно числу уравнений в системе и которые обозначаются через ;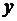

3. Экзогенные переменные – это:

а) предопределенные переменные, влияющие на зависимые переменные, но не зависящие от них, обозначаются через ;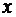

4. Лаговые переменные – это:

в) значения зависимых переменных за предшествующий период времени.

5. Для определения параметров структурную форму модели необходимо преобразовать в:

а) приведенную форму модели;

6. Модель идентифицируема, если:

в) если число параметров структурной модели равно числу параметров приведенной формы модели.

7. Модель неидентифицируема, если:

а) число приведенных коэффициентов меньше числа структурных коэффициентов;

8. Модель сверхидентифицируема, если:

б) если число приведенных коэффициентов больше числа структурных коэффициентов;

9. Уравнение идентифицируемо, если:

б) ;

10. Уравнение неидентифицируемо, если:

а) ;

11. Уравнение сверхидентифицируемо, если:

в) .

12. Для определения параметров точно идентифицируемой модели:

б) применяется косвеный МНК;.

13. Для определения параметров сверхидентифицируемой модели:

а) применяется двушаговый МНК;

14. Для определения параметров неидентифицируемой модели:

б) ни один из существующих методов применить нельзя.

Временные ряды

1. Аддитивная модель временного ряда имеет вид:

б) ;

2. Мультипликативная модель временного ряда имеет вид:

а) ;

3. Коэффициент автокорреляции:

а) характеризует тесноту линейной связи текущего и предыдущего уровней ряда;

4. Аддитивная модель временного ряда строится, если:

а) значения сезонной компоненты предполагаются постоянными для различных циклов;

5. Мультипликативная модель временного ряда строится, если:

б) амплитуда сезонных колебаний возрастает или уменьшается;

6. На основе поквартальных данных построена аддитивная модель временного ряда. Скорректированные значения сезонной компоненты за первые три квартала равны: 7 – I квартал, 9 – II квартал и –11 – III квартал. Значение сезонной компоненты за IV квартал есть:

7. На основе поквартальных данных построена мультипликативная модель временного ряда. Скорректированные значения сезонной компоненты за первые три квартала равны: 0,8 – I квартал, 1,2 – II квартал и 1,3 – III квартал. Значение сезонной компоненты за IV квартал есть:

8. Критерий Дарбина-Уотсона применяется для:

Источник

Ответы по эконометрике

Каждое следующее значение остатков

Y=T+S+E

Амплитуда сезонных колебаний возрастает и уменьшается

индентифицируемое

Как случайные величины

От 0 до 1

Иметь нормальный закон…..

Парного коэф. корреляции

Не превосходит единицы

Если относительная величина……………………неограниченно

Fрасч>Fтабл

Интервал содержит параметры генеральной совокупности

Неэффективные оценки параметров

Уt=a+b0x1+Ɣyt-1+ƹt

Уt= a+b0x1…….(самая длинная формула)

Дисперсия случайных….

b±t…….·ob если коэф. «а» вместо «в» «а»

среднее значение у=2……………….равняется: (если у=6, тогда ответ 2)

…….(xi-x¯)²)

Вероятность того, что………………..прогнозный интервал

t тест

Большее значения F критерия

…………..=[(n-m-1)/m]( R²/(1- R²)]

Приведенную форму модели

Применяется косвенный МНК

Применяется двухшаговый МНК

Ни один из существ. методов применить нельзя

11 атрибутивных методов

С ростом Х увеличивается У

T статистки

R=√ D

T критерия стьюдента

Статистическую значимость модели в целом……

Ситуция не определена

Функциональная зависимость

Принимает любое значение

Квадрат парного…

Имеют нормальный закон

Степенная

коэф. корреляции

Коэф. детерминации

Определения тесноты связи……………..

Стоящие в начале и в конце временного ряда

Характеризует тесноту линейной связи текущего и предыдущего уровней ряда

Значение зависимых переменных за предшествующий период времени

Две и больше независимых…………

Y=TxSxE

Ошибками спецификации

Математическое ожидание остатков равно 0

Оценки обладают наименьшей дисперсией………….оценками

Увелич. точность….

Корреляция между независимыми переменными

b= Cov(x;y)/Var(x);a=y¯ ­bx¯

От количества точек………………(или от применяемого метода сглаживания)

Применим после ее…..

Применим после ее приведения

тенденцией

На сколько % изменится результирующий показатель у при изменении хi на 1%при неизмененном среднем уровне других факторов

RC²= R² (n-1)/(n-m-1)

T стьюдента

периодическим

И от уровня доверительной вероятности,и от числа факторов, вкл-х в модель и от длины исходного ряда

Только от уровня доверительной вероятности и от числа факторов, вкл-х в модель

Длительные, постоянно действующие факторы

По методу наименьших квадратов

D+1=H

D+1 H

Атрибутивные признаки….

Проверки существенности коэф. корреляции

На сколько единиц изменится У, если Х изменился на единицу

На сколько % изменится……………………………на 1%

Единица измерения фактора…………………показателя

Зависимые переменные, число которых равно числу уравнений……..

Предопределенные переменные, влияющие…………..

Методу наименьших квадратов

Источник

Ответы на тесты по эконометрике

Q=………..min соответствует методу наименьших квадратов

Автокорреляция — это корреляционная зависимость уровней ряда от предыдущих значений.

Автокорреляция имеется когда каждое следующее значение остатков

Аддитивная модель временного ряда имеет вид: Y=T+S+E

Атрибутивная переменная может употребляться, когда: независимая переменная качественна;

В каких пределах изменяется коэффициент детерминанта: от 0 до 1.

В каком случае модель считается адекватной Fрасч>Fтабл

В каком случае рекомендуется применять для моделирования показателей с увелич. ростом параболу если относительная величина…неограниченно

В результате автокорреляции имеем неэффективные оценки параметров

В хорошо подобранной модели остатки должны иметь нормальный закон

В эконометрическом анализе Xj рассматриваются как случайные величины

Величина доверительного интервала позволяет установить предположение о том, что: интервал содержит оценку параметра неизвестного.

Величина рассчитанная по формуле r=…является оценкой парного коэф. Корреляции

Внутренне нелинейная регрессия — это истинно нелинейная регрессия, которая не может быть приведена к линейной регрессии преобразованием переменных и введением новых переменных.

Временной ряд — это последовательность значений признака (результативного переменного), принимаемых в течение последовательных моментов времени или периодов.

Выберете авторегрессионную модель Уt=a+b0x1+Ɣyt-1+ƹt

Выберете модель с лагами Уt= a+b0x1…….(самая длинная формула)

Выборочное значение Rxy не > 1, |R|

Гетероскедастичность присутствует когда: дисперсия случайных остатков не постоянна

Гетероскидастичность – это когда дисперсия остатков различна

Гипотеза об отсутствии автокорреляции остатков доказана, если Dтабл2…

Гомоскедастичность — постоянство дисперсии для всех наблюдений, или одинаковость дисперсии каждого отклонения (остатка) для всех значений факторных переменных.

Гомоскидастичность – это когда дисперсия остатков постоянна и одинакова для всех … наблюдений.

Дисперсия — показатель вариации.

Для определения параметров неиденцифицированной модели применяется.: не один из сущ. методов применить нельзя

Для определения параметров сверх иденцифицированной модели примен.: применяется. 2-х шаговый МНК

Для определения параметров структурную форму модели необходимо преобразовать в приведенную форму модели

Для определения параметров точно идентифицируемой модели: применяется косвенный МНК;

Для оценки … изменения y от x вводится: коэффициент эластичности:

Для парной регрессии ơ²b равно ….(xi-x¯)²)

Для проверки значимости отдельных параметров регрессии используется: t-тест.

Для регрессии y=a+bx из n наблюдений интервал доверия (1-а)% для коэф. b составит b±t…….·ơb

Для регрессии из n наблюдений и m независимых переменных существует такая связь между R² и F..=[(n-m-1)/m]( R²/(1- R²)]

Доверительная вероятность – это вероятность того, что истинное значение результативного показателя попадёт в расчётный прогнозный интервал.

Допустим что для описания одного экономического процесса пригодны 2 модели. Обе адекватны по f критерию фишера. какой предоставить преимущество, у той у кот.: большее значения F критерия

Допустим, что зависимость расходов от дохода описывается функцией y=a+bx среднее значение у=2…равняется 9

Если Rxy положителен, то с ростом x увеличивается y.

Если в уравнении регрессии имеется несущественная переменная, то она обнаруживает себя по низкому значению T статистки

Если качественный фактор имеет 3 градации, то необходимое число фиктивных переменных 2

Если коэффициент корреляции положителен, то в линейной модели с ростом х увеличивается у

Если мы заинтересованы в использовании атрибутивных переменных для отображения эффекта разных месяцев мы должны использовать 11 атрибутивных методов

Если регрессионная модель имеет показательную зависимость, то метод МНК применим после приведения к линейному виду.

Зависимость между коэффициентом множественной детерминации (D) и корреляции (R) описывается следующим методом R=√D

Значимость уравнения регрессии — действительное наличие исследуемой зависимости, а не просто случайное совпадение факторов, имитирующее зависимость, которая фактически не существует.

Интеркорреляция и связанная с ней мультиколлинеарность — это приближающаяся к полной линейной зависимости тесная связь между факторами.

Какая статистическая характеристика выражается формулой R²=…коэффициент детерминации

Какая статистическая хар-ка выражена формулой : r_xy=Ca(x;y) разделить на корень Var(x)*Var(y): коэффициент. корреляции

Какая функция используется при моделировании моделей с постоянным ростом степенная

Какие точки исключаются из временного ряда процедурой сглаживания и в начале, и в конце.

Какое из уравнений регрессии является степенным y=a˳aͯ¹a

Классический метод к оцениванию параметров регрессии основан на: – метод наименьших квадратов (МНК)

Количество степеней свободы для t статистики при проверки значимости параметров регрессии из 35 наблюдений и 3 независимых переменных 31;

Количество степеней свободы знаменателя F-статистики в регрессии из 50 наблюдений и 4 независимых переменных: 45

Компоненты вектора Ei имеют нормальный закон

Корреляция — стохастическая зависимость, являющаяся обобщением строго детерминированной функциональной зависимости посредством включения вероятностной (случайной) компоненты.

Коэффициент автокорреляции: характеризует тесноту линейной связи текущего и предстоящего уровней ряда

Коэффициент детерминации — показатель тесноты стохастической связи в общем случае нелинейной регрессии

Коэффициент детерминации – это величина, которая характеризует связь между зависимыми и независимыми переменными.

Коэффициент детерминации – это квадрат множественного коэффициента корреляции

Коэффициент детерминации – это: величина, которая характеризует связь между независимой и зависимой (зависящей) переменными;

Коэффициент детерминации R показывает долю вариаций зависимой переменной y, объяснимую влиянием факторов, включаемых в модель.

Коэффициент детерминации изменяется в пределах: – от 0 до 1

Коэффициент доверия — это коэффициент, который связывает линейной зависимостью предельную и среднюю ошибки, выясняет смысл предельной ошибки, характеризующей точность оценки, и является аргументом распределения (чаще всего, интеграла вероятностей). Именно эта вероятность и есть степень надежности оценки.

Коэффициент доверия (нормированное отклонение) — результат деления отклонения от среднего на стандартное отклонение, содержательно характеризует степень надежности (уверенности) полученной оценки.

Коэффициент корелляции Rxy используется для определения полноты связи X и Y.

Коэффициент корелляции равный 0 означает, что: –отсутствует линейная связь.

Коэффициент корреляции используется для: определения тесноты связи между случайными величинами X и Y;

Коэффициент корреляции рассчитывается для измерения степени линейной взаимосвязи между двумя случайными переменными.

Коэффициент линейной корреляции — показатель тесноты стохастической связи между фактором и результатом в случае линейной регрессии.

Коэффициент регрессии — коэффициент при факторной переменной в модели линейной регрессии.

Коэффициент регрессии b показывает: на сколько единиц увеличивается y, если x увеличивается на 1.

Коэффициент эластичности измеряется в: неизмеримая величина.

Критерий Дарвина-Чотсона применяется для: – отбора факторов в модель; или – определения автокорреляции в остатках

Критерий Стьюдента — проверка значимости отдельных коэффициентов регрессии и значимости коэффициента корреляции.

Критерий Фишера показывает статистическую значимость модели в целом на основе совокупной достоверности всех ее коэффициентов;

Лаговые переменные это значение зависимых переменных за предшествующий период времени

Модель в целом статистически значима, если Fрасч > Fтабл.

Модель идентифицирована, если: – число параметров структурной модели равно числу параметров приведён. формы модели.

Модель неидентифицирована, если: – число приведён. коэф . больше числа структурных коэф.

Модель сверхидентифицирована, если: число приведён. коэф. меньше числа структурных коэф

Мультипликативная модель временного ряда имеет вид: – Y=T*S*E

Мультипликативная модель временного ряда строится, если: амплитуда сезонных колебаний возрастает или уменьшается

На основе поквартальных данных…значения 7-1 квартал, 9-2квартал и 11-3квартал …-5

Неправильный выбор функциональной формы или объясняющих переменных называется ошибками спецификации

Несмещённость оценки параметра регрессии, полученной по МНК, означает: – что она характеризуется наименьшей дисперсией.

Одной из проблем которая может возникнуть в многофакторной регрессии и никогда не бывает в парной регрессии, является корреляция между независимыми переменными

От чего зависит количество точек, исключаемых из временного ряда в результате сглаживания: от применяемого метода сглаживания.

Отметьте основные виды ошибок спецификации: отбрасывание значимой переменной; добавление незначимой переменной;

Оценки коэффициентов парной регрессии является несмещённым, если: математические ожидания остатков =0.

Оценки параметров парной линейной регрессии находятся по формуле b= Cov(x;y)/Var(x);a=y¯ ­bx¯

Оценки параметров регрессии являются несмещенными, если Математическое ожидание остатков равно 0

Оценки парной регрессии явл. эффективными, если: оценка обладают наименьшей дисперсией по сравнению с другими оценками

При наличии гетероскедастичности следует применять: – обобщённый МНК

При проверке значимости одновременно всех параметров регрессии используется: F-тест.

Применим ли метод наименьших квадратов для расчетов параметров показательной зависимости применим после ее приведения

Применим ли метод наименьших квадратов(МНК) для расчёта параметров нелинейных моделей? применим после её специального приведения к линейному виду

С помощью какого критерия оценивается значимость коэффициента регрессии T стьюдента

С увеличением числа объясняющих переменных скоррестированный коэффициент детерминации: – увеличивается.

Связь между индексом множественной детерминации R² и скорректированным индексом множественной детерминации Ȓ² есть

Скорректиров. коэф. детерминации: – больше обычного коэф. детерминации

Стандартизованный коэффициент уравнения регрессии Ƀk показывает на сколько % изменится результирующий показатель у при изменении хi на 1%при неизмененном среднем уровне других факторов

Стандартный коэффициент уравнения регрессии: показывает на сколько 1 изменится y при изменении фактора xk на 1 при сохранении др.

Суть коэф. детерминации r 2 _xy состоит в следующем: – характеризует долю дисперсии результативного признака y объясняем. регресс., в общей дисперсии результативного признака.

Табличные значения Фишера (F) зависят от доверительной вероятности и от числа включённых факторов и от длины исходного ряда (от доверительной вероятности p и числа степеней свободы дисперсий f1 и f2)..

Уравнение в котором H число эндогенных переменных, D число отсутствующих экзогенных переменных, идентифицируемо если D+1=H

Уравнение в котором H число эндогенных переменных, D число отсутствующих экзогенных переменных, НЕидентифицируемо если D+1 H

Уравнение идентифицировано, если: – D+1=H

Уравнение неидентифицировано, если: – D+1 H

Фиктивные переменные – это: атрибутивные признаки (например, как профессия, пол, образование), которым придали цифровые метки;

Формула t= rxy….используется для проверки существенности коэффициента корреляции

Частный F-критерий: – оценивает значимость уравнения регрессии в целом

Число степеней свободы для факторной суммы квадратов в линейной модели множественной регрессии равно: m;

Что показывает коэффициент наклона – на сколько единиц изменится у, если х изменился на единицу,

Что показывает коэффициент. абсолютного роста на сколько единиц изменится у, если х изменился на единицу

Экзогенная переменная – это независимая переменная или фактор-Х.

Экзогенные переменные — это переменные, которые определяются вне системы и являются независимыми

Экзогенные переменные – это предопределенные переменные, влияющие на зависимые переменные (Эндогенные переменные), но не зависящие от них, обозначаются через х

Эластичность измеряется единица измерения фактора…показателя

Эндогенные переменные – это: зависимые переменные, число которых равно числу уравнений в системе и которые обозначаются через у

Определения

T-отношение (t-критерий) — отношение оценки коэффициента, полученной с помощью МНК, к величине стандартной ошибки оцениваемой величины.

Аддитивная модель временного ряда – это модель, в которой временной ряд представлен как сумма перечисленных компонент.

Критерий Фишера — способ статистической проверки значимости уравнения регрессии, при котором расчетное (фактическое) значение F-отношения сравнивается с его критическим (теоретическим) значением.

Линейная регрессия — это связь (регрессия), которая представлена уравнением прямой линии и выражает простейшую линейную зависимость.

Метод инструментальных переменных — это разновидность МНК. Используется для оценки параметров моделей, описываемых несколькими уравнениями. Главное свойство — частичная замена непригодной объясняющей переменной на такую переменную, которая некоррелированна со случайным членом. Эта замещающая переменная называется инструментальной и приводит к получению состоятельных оценок параметров.

Метод наименьших квадратов (МНК) — способ приближенного нахождения (оценивания) неизвестных коэффициентов (параметров) регрессии. Этот метод основан на требовании минимизации суммы квадратов отклонений значений результата, рассчитанных по уравнению регрессии, и истинных (наблюденных) значений результата.

Множественная линейная регрессия — это множественная регрессия, представляющая линейную связь по каждому фактору.

Множественная регрессия — регрессия с двумя и более факторными переменными.

Модель идентифицируемая — модель, в которой все структурные коэффициенты однозначно определяются по коэффициентам приведенной формы модели.

Модель рекурсивных уравнений — модель, которая содержит зависимые переменные (результативные) одних уравнений в роли фактора, оказываясь в правой части других уравнений.

Мультипликативная модель – модель, в которой временной ряд представлен как произведение перечисленных компонент.

Несмещенная оценка — оценка, среднее которой равно самой оцениваемой величине.

Нулевая гипотеза — предположение о том, что результат не зависит от фактора (коэффициент регрессии равен нулю).

Обобщенный метод наименьших квадратов (ОМНК) — метод, который не требует постоянства дисперсии (гомоскедастичности) остатков, но предполагает пропорциональность остатков общему множителю (дисперсии). Таким образом, это взвешенный МНК.

Объясненная дисперсия — показатель вариации результата, обусловленной регрессией.

Объясняемая (результативная) переменная — переменная, которая статистически зависит от факторной переменной, или объясняющей (регрессора).

Остаточная дисперсия — необъясненная дисперсия, которая показывает вариацию результата под влиянием всех прочих факторов, неучтенных регрессией.

Предопределенные переменные — это экзогенные переменные системы и лаговые эндогенные переменные системы.

Приведенная форма системы — форма, которая, в отличие от структурной, уже содержит одни только линейно зависящие от экзогенных переменных эндогенные переменные. Внешне ничем не отличается от системы независимых уравнений.

Расчетное значение F-отношения — значение, которое получают делением объясненной дисперсии на 1 степень свободы на остаточную дисперсию на 1 степень свободы.

Регрессия (зависимость) — это усредненная (сглаженная), т.е. свободная от случайных мелкомасштабных колебаний (флуктуаций), квазидетерминированная связь между объясняемой переменной (переменными) и объясняющей переменной (переменными). Эта связь выражается формулами, которые характеризуют функциональную зависимость и не содержат явно стохастических (случайных) переменных, которые свое влияние теперь оказывают как результирующее воздействие, принимающее вид чисто функциональной зависимости.

Регрессор (объясняющая переменная, факторная переменная) — это независимая переменная, статистически связанная с результирующей переменной. Характер этой связи и влияние изменения (вариации) регрессора на результат исследуются в эконометрике.

Система взаимосвязанных уравнений — это система одновременных или взаимозависимых уравнений. В ней одни и те же переменные выступают одновременно как зависимые в одних уравнениях и в то же время независимые в других. Это структурная форма системы уравнений. К ней неприменим МНК.

Система внешне не связанных между собой уравнений — система, которая характеризуется наличием одних только корреляций между остатками (ошибками) в разных уравнениях системы.

Случайный остаток (отклонение) — это чисто случайный процесс в виде мелкомасштабных колебаний, не содержащий уже детерминированной компоненты, которая имеется в регрессии.

Состоятельные оценки — оценки, которые позволяют эффективно применять доверительные интервалы, когда вероятность получения оценки на заданном расстоянии от истинного значения параметра становится близка к 1, а точность самих оценок увеличивается с ростом объема выборки.

Спецификация модели — определение существенных факторов и выявление мультиколлинеарности.

Стандартная ошибка — среднеквадратичное (стандартное) отклонение. Оно связано со средней ошибкой и коэффициентом доверия.

Степени свободы — это величины, характеризующие число независимых параметров и необходимые для нахождения по таблицам распределений их критических значений.

Тренд — основная тенденция развития, плавная устойчивая закономерность изменения уровней ряда.

Уровень значимости — величина, показывающая, какова вероятность ошибочного вывода при проверке статистической гипотезы по статистическому критерию.

Фиктивные переменные — это переменные, которые отражают сезонные компоненты ряда для какого-либо одного периода.

Эконометрическая модель — это уравнение или система уравнений, особым образом представляющие зависимость (зависимости) между результатом и факторами. В основе эконометрической модели лежит разбиение сложной и малопонятной зависимости между результатом и факторами на сумму двух следующих компонентов: регрессию (регрессионная компонента) и случайный (флуктуационный) остаток. Другой класс эконометрических моделей образует временные ряды.

Эффективность оценки — это свойство оценки обладать наименьшей дисперсией из всех возможных.

Источник