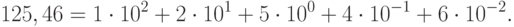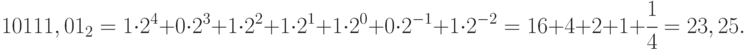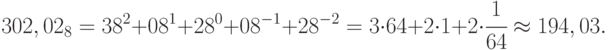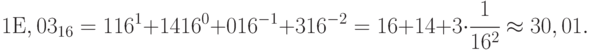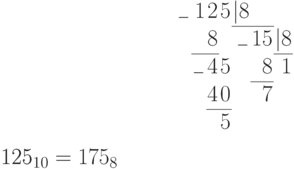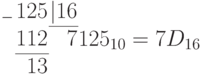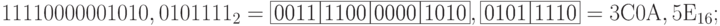Двоичная система счисления

Двоичная система — это один из видов позиционных систем счисления. Основание данной системы равно двум, то есть используется только два символа для записи чисел.

Немного истории

Впервые о данной системе чисел заговорил основоположник математического анализа Г.В. Лейбниц еще в XVII веке. Он доказал, что для данного множества действуют все арифметические операции: сложение, вычитание, умножение и даже деление. Однако вплоть до 30-х годов XX века данную систему не рассматривали всерьез. Но с развитием электронных устройств и ЭВМ, ученые вновь принялись к изучению данной темы, так как двоичная система отлично подходила для программирования и организации хранения данных в памяти компьютеров.

Таблица и алфавит

Кроме того, двоичная система является самой удобной для быстрого перевода в другие системы счисления.

100110₂ = 1 ∙ 2 5 + 0 ∙ 2 4 + 0 ∙ 2 3 + 1 ∙ 2 2 + 1 ∙ 2 2 + 0 ∙ 2 0 = 32 + 0 + 0 + 4 + 2 + 0 = 38₁₀

Чтобы наоборот перевести число в двоичную из десятичной, необходимо выполнить его деление на 2 с остатком, а затем записать все остатки в обратном порядке, начиная с частного:

Делимое	38	19	9	4	2
Делитель	2	2	2	2	2
Частное	19	9	4	2	1
Остаток	0	1	1	0	0

Для перевода в другие системы необходимо:

Однако можно воспользоваться и более быстрым и удобным способом: разделить знаки двоичного числа на условные группы слева на право (для восьмеричной — по 3 знака; для шестнадцатеричной — по 4 знака), а затем воспользоваться таблицей перевода:

Двоичная	Восьмеричная	Шестнадцатеричная
0	0	0
001	1	1
010	2	2
011	3	3
100	4	4
101	5	5
110	6	6
111	7	7
1000	8
1001	9
1010	A
1011	B
1100	C
1101	D
1110	E
1111	F

11001001₂ = 11 001 001 = 011 001 001 = 311₈

11001001₂ = 1100 1001 = С9₁₆

Представление двоичных чисел

В двоичной системе также существует понятие «отрицательных» чисел. И для того, чтобы провести какую-либо операцию с ними в двоичном коде, необходимо представить его в виде дополнительного кода. Запись положительного числа при этом не меняется ни для одного из кодов.

Чтобы найти дополнительный код отрицательного числа, необходимо воспользоваться его прямым и дополнительным кодами.

Прямой код предполагает приписывание единицы в начале без изменений записи:

A > 0	Aпр = 0A	1010112; Aпр = 01010112
A ≤ 0	Aпр = 1|A|	-1010112; Aпр = 11010112

Для записи обратного кода цифры заменяют на противоположное значение, первую единицу от прямого кода оставляют без изменений:

A > 0	Aобр = 0A	1010112; Aобр = 01010112
A ≤ 0	Aобр = 1 A	-1010112; Aобр = 10101002

Дополнительный код предполагает использование обратного кода, с той лишь разницей, что к отрицательному числу прибавляют единицу:

A > 0	Aдоп = 0A	1010112; Aдоп = 01010112
A ≤ 0	Aдоп = 1 A + 1	-1010112; Aдоп = 10101012

Применение двоичной системы в информатике

Двоичная система получила особое распространение в программировании цифровых устройств, так как она соответствует требованиям многих технических устройств, поддерживающих два состояния (есть ток, нет тока). Кроме того, является более простой и надежной для кодирования информации. Именно поэтому программный код большей части ЭВМ основан именно на двоичной системе счисления.

Источник

Двоичная форма целых чисел. Количество информации

Внутреннее представление данных

ЭВМ является электрическим прибором. Она управляется с помощью электрических сигналов. Поэтому любые данные должны быть некоторым универсальным образом представлены в таком виде, чтобы их можно было легко перевести на «электрический» язык. Таким свойством обладают двоичная форма целых чисел. Для записи числа в двоичной форме используются только два символа 0 и 1. Эти символы легко поставить в соответствие некоторому фиксированному значению напряжения в электрических схемах ЭВМ (см. рис. 1.3).

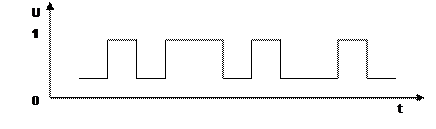
Рис. 1.3 Поток данных в двоичной форме

Чтобы обрабатывать данные, необходимо иметь некоторый универсальный способ представления операций с целыми числами, чтобы эти операции были легко представимы на «электрическом» языке. Оказывается, что этому условию удовлетворяют три операции с двоичными числами. Это операции логического сложения «ИЛИ», логического умножения «И» и отрицания «НЕ».

Таблица 1.1 Операции с двоичными числами

Таким образом, все данные, с которыми работают ЭВМ, представлены в виде двоичных чисел, а все действия с данными сводятся к комбинации трёх логических операций.

Рассмотрим сложение чисел 4+3. В двоичной форме эти числа будут иметь вид соответственно 0100 и 0011. Выполняя операцию логического сложения с каждым разрядом обоих чисел, получим число 0111, что является двоичным представлением числа 7.

Количество информации, соответствующее двоичному числу, называют битом [bit]. Число, которое представлено N битами называется N-битным или N-разрядным.

В дальнейшем оказалось удобным оперировать последовательностями нулей и единиц, объединённых в группы фиксированного размера.

Очень часто программистам приходится непосредственно работать с двоичными числами, поэтому, чтобы упростить эту работу, часто используются шестнадцатеричное представление двоичных чисел.

Для упрощения перевода целых чисел в двоичную и шестнадцатеричную формы составляется следующая таблица:

Х10	Х2	Х16	Х10	Х2	Х16
A
B
C
D
E
F

Таким образом, первая задача, которая ставится в информатике – это задача представления любых данных в форме целых чисел (в цифровой форме).

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Двоичная система счисления

Содержание:

Вспомним материал по системам счисления. В нём говорилось, что наиболее удобной системой счисления для компьютерных систем является двоичная система. Дадим определение этой системе:

Двоичной системой счисления называется позиционная система счисления, у которой основанием является число 2.

Для записи любого числа в двоичной системе счисления используются всего лишь 2 цифры: 0 и 1.

Общая форма записи двоичных чисел

Для целых двоичных чисел можно записать:

Данная форма записи числа «подсказывает» правило перевода натуральных двоичных чисел в десятичную систему счисления: требуется вычислить сумму степеней двойки, соответствующих единицам в свёрнутой форме записи двоичного числа.

Правила сложения двоичных чисел

Основные правила сложения однобитовых чисел

Отсюда видно, что и, как и в десятичной системе счисления, числа, представленные в двоичной системе счисления, складывают поразрядно. Если разряд переполняется, единица переносится в следующий разряд.

Пример сложения двоичных чисел

Правила вычитания двоичных чисел

Но как быть с 0-1=? Вычитание двоичных чисел немного отличается от вычитания десятичных чисел. Для этого используется несколько способов.

Вычитание методом заимствования

Запишите двоичные числа друг под другом – меньшее число под большим. Если меньшее число имеет меньше цифр, выровняйте его по правому краю (так, как вы записываете десятичные числа при их вычитании).
Некоторые задачи на вычитание двоичных чисел ничем не отличаются от вычитания десятичных чисел. Запишите числа друг под другом и, начиная справа, найдите результат вычитания каждой пары чисел.

Вот несколько простых примеров:

Вычтите цифры в оставшихся столбцах. Теперь это легко сделать (работайте со столбцами, двигаясь, справа налево):

Вычитание методом дополнения

Запишите двоичные числа друг под другом так, как вы записываете десятичные числа при их вычитании. Этот метод используется компьютерами для вычитания двоичных чисел, так как он основан на более эффективном алгоритме.

Однако простому человеку, привыкшему вычитать десятичные числа, этот метод может показаться более сложным (если вы программист, обязательно познакомьтесь с этим методом вычитания двоичных чисел).

Если значность чисел разная, к числу с меньшей значностью слева припишите соответствующее количество 0.

В вычитаемом числе поменяйте цифры: каждую 1 поменяйте на 0, а каждый 0 на 1.

011101₂ → 100010₂.

К полученному вычитаемому прибавьте единицу.

100010₂+ 1₂ = 100011₂

Теперь вместо вычитания сложите два двоичных числа.

Проверьте ответ. Быстрый способ – откройте двоичный онлайн калькулятор и введите в него вашу задачу. Два других метода подразумевают проверку ответа вручную.

1) Переведем числа в двоичную систему счисления:
Допустим, что из числа 101101₂ нужно вычесть 11011₂

2) Обозначим как A число 101101₂ и как B число 11011₂.

3) Запишем числа A и B столбиком, одно под другим, начиная с младших разрядов (нумерация разрядов начинается с нуля).

Источник

СТРАННАЯ ДЕВОЧКА

Но станет всё совсем обычным,
Когда поймёте наш рассказ.

С помощью двоичной системы кодирования можно зафиксировать любые данные и знания. Это легко понять, если вспомнить принцип кодирования и передачи информации с помощью азбуки Морзе.

Объём памяти компьютера измеряется в байтах. Каждый байт может выражать букву, число, пробел, знак препинания или какой-либо другой символ. Количество символов, которые компьютер может хранить в оперативной памяти, меняется в широких пределах от вида компьютера и его модели.

Объём памяти, хотя он и измеряется в байтах, обычно выражается в килобайтах. Слово «килобайт», вообще говоря, означает «1000 байт». (Напомним, что приставка «кило» означает «тысяча».)

Фактически же килобайт равен 1024 байтам: 1 Кбайт = 1024 байт.

Компьютер с объёмом памяти в 64 К может хранить 64 х 1024 = 65536 символов.

Объём памяти первых микрокомпьютеров составлял всего лишь 2 Кб. Нынешние компьютеры имеют объём памяти 128, 256, 512, 1024 Мб и более

Объём памяти новейших компьютеров так велик, что она выражается в гигабайтах, т. е. в миллиардах байтов.

1 Мбайт = 1024 Кбайт = 1 048 576 байт.

Итак, каждый символ алфавитно-цифровой информации представляется в компьютере кодом из восьми двоичных цифр. Следовательно, каждый символ в компьютере имеет код объёмом 1 байт.

Информатика и образование

имеет в двоичной форме объём 25 байт: 23 буквы и 2 символа «пробел» по 1 байту.

61 байт * 45 строк = 2745 байт.

Так как в книге 258 страниц текста и на каждой странице в среднем по 2745 байт информации, то объём алфавитно-цифровой информации в книге

2745 байт * 258 страниц = 708210 байт » 692 Кбайт

Таким образом, текст книги имеет объём около 692 Кбайт.

Перевод чисел

Для перевода десятичного числа в двоичное надо разделить его на 2 и собрать остатки, начиная с последнего частного.

А вот как происходит перевод двоичного числа в десятичное:

ДРОБНЫЕ ЧИСЛА В ДВОИЧНОЙ СИСТЕМЕ СЧИСЛЕНИЯ

В любой системе счисления нужно уметь представлять не только целые числа, но и дробные. С математической точки зрения это ординарная задача, которая давно решена. Однако с точки зрения компьютерной техники это далеко не тривиальная проблема, во многом связанная с архитектурой компьютера. Ресурсы компьютеров не бесконечны, и основной трудностью является представление периодических и непериодических дробей. Следовательно, такие дроби следует округлять, задавать класс точности участвующих (и могущих появиться в результате вычислений!) чисел без потери точности вычислений, а также следить за тем, чтобы потеря точности не произошла при переводе чисел из одной системы счисления в другую. Особенно важно аккуратно производить вычисления при операциях с плавающей точкой.

Запишем формулу представления дробного числа в позиционной системе счисления:

В случае десятичной системы счисления получим:

Перевод дробного числа из двоичной системы счисления в десятичную производится по следующей схеме:

Перевод дробного числа из десятичной системы счисления в двоичную осуществляется по следующему алгоритму:

· Вначале переводится целая часть десятичной дроби в двоичную систему счисления;

· Затем дробная часть десятичной дроби умножается на основание двоичной системы счисления;

· В полученном произведении выделяется целая часть, которая принимается в качестве значения первого после запятой разряда числа в двоичной системе счисления;

· Алгоритм завершается, если дробная часть полученного произведения равна нулю или если достигнута требуемая точность вычислений. В противном случае вычисления продолжаются с предыдущего шага.

Пример: Требуется перевести дробное десятичное число 206,116 в дробное двоичное число.

Перевод целой части дает 206₁₀=11001110₂ по ранее описанным алгоритмам; дробную часть умножаем на основание 2, занося целые части произведения в разряды после запятой искомого дробного двоичного числа:

.792 • 2 = 1 .584

Получим: 206,116₁₀=11001110,0001110011₂

Таблицу степеней первых восьми отрицательных степеней двойки

Двоичная арифметика

Над числами в двоичной системе счисления можно выполнять арифметические действия.

Источник

Двоичные числа и двоичная арифметика

Принцип представления чисел в позиционных системах счисления

Позиционной называется система счисления, в которой вес разряда числа определяется его позицией в записи числа [1].

сотни десятки единицы десятые доли сотые доли

Аналогично любое число в десятичной системе счисления можно представить в виде подобной суммы:

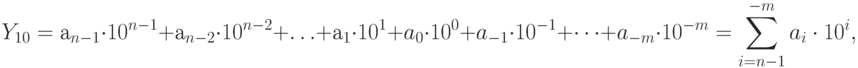( 11.1)

Для числа в системе счисления с основанием выражение (11.1) преобразуется к виду:

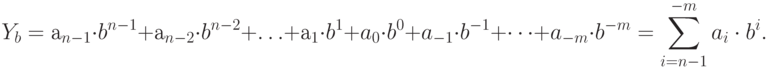( 11.2)

Таблица 11.1. Параметры позиционных систем счисления

Название системы счисления	Основание системы счисления	Знаки, использующиеся для записи чисел
Двоичная	2	0, 1
Троичная	3	0, 1, 2
Четверичная	4	0, 1, 2, 3
…	…	…
Восьмеричная	8	0, 1, 2, 3, 4, 5, 6, 7
…	…	…
Десятичная	10	0, 1, 2, 3, 4, 5, 6, 7, 8, 9
…	…	…
Шестнадцатеричная	16	0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
…	…	…

Приведем примеры записи чисел в указанных системах и найдем их десятичные эквиваленты по формуле (11.2).

Для двоичного числа:

Для восьмеричного числа:

Для шестнадцатеричного числа:

Округление относится к дробной части числа, целая часть переводится точно. Особенностью перевода из шестнадцатеричного кода в десятичный код является то, что в качестве коэффициента используется десятичный эквивалент шестнадцатеричного знака в соответствии с таблицей 11.2. Для нашего примера вместо знака » » в расчетную формулу (11.2) подставляется десятичное число .

Из рассмотренных примеров видно, что общая формула (11.2) может использоваться для перевода числа из системы счисления с любым основанием в десятичную.

Перевод чисел из одной системы счисления в другую

Перевод из десятичной системы в любую другую. Перевод целых чисел

Проверка перевода осуществляется по формуле (11.2), так, как это показано ниже на примерах.

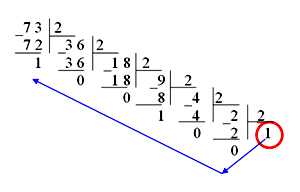
Пример. Перевести десятичное число 125 в двоичную, восьмеричную и шестнадцатеричную системы счисления. Проверить результаты по формуле (П11.2).

В рассмотренном примере при переводе вместо коэффициента используется его десятичный эквивалент в соответствии с таблицей 11.2.

Перевод из двоичной системы в шестнадцатеричную (восьмеричную)

Как уже было сказано выше, шестнадцатеричный и восьмеричный коды используются для более компактной и удобной записи двоичных чисел. Так, программирование в машинных кодах осуществляется в большинстве случаев в шестнадцатеричном коде. Правила перевода для шестнадцатеричной и восьмеричной системы структурно одинаковы, отличия для восьмеричной системы отображаются в скобках.

Двоичная запись числа делится на группы по четыре ( три ) двоичных знака влево и вправо от запятой, отделяющей целые и дробные части Неполные крайние группы (если они есть) дополняются нулями до четырех ( трех ) знаков. Каждая группа заменяется одним шестнадцатеричным ( восьмеричным ) знаком в соответствии с кодом группы (табл. 11.2).

Таблица 11.2. Соответствие двоичных групп, шестнадцатеричных и восьмеричных знаков

Двоичная группа	Шестнадцатеричный знак	Десятичный эквивалент	Двоичная группа	Восьмеричный знак
0000	0	0	000	0
0001	1	1	001	1
0010	2	2	010	2
0011	3	3	011	3
0100	4	4	100	4
0101	5	5	101	5
0110	6	6	110	6
0111	7	7	111	7
1000	8	8
1001	9	9
1010	A	10
1011	B	11
1100	C	12
1101	D	13
1110	E	14
1111	F	15

Перевод из шестнадцатеричной (восьмеричной) системы в двоичную

Каждая цифра (без всяких сокращений!) шестнадцатеричного ( восьмеричного ) числа заменяется одной двоичной группой из четырех ( трех ) двоичных знаков (табл. 11.2).

Как показано в примерах, крайние нули слева и справа при желании можно не писать, но такое сокращение делается уже после перевода в двоичную систему.

Источник