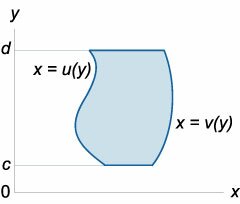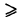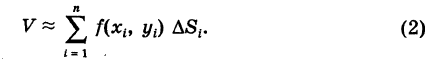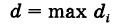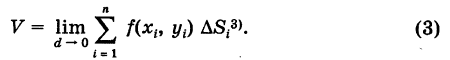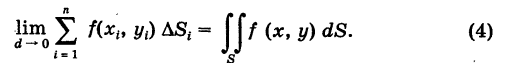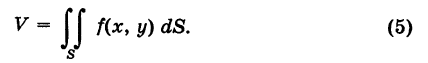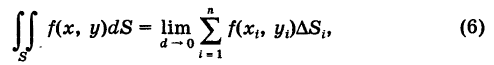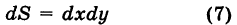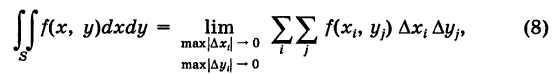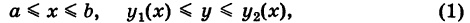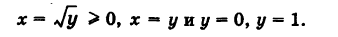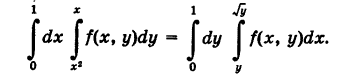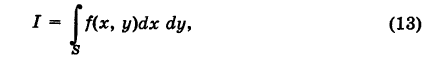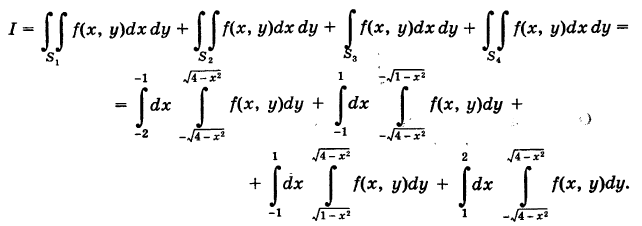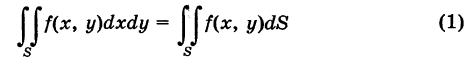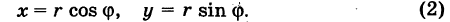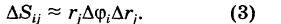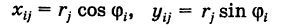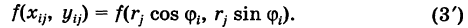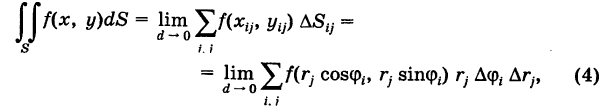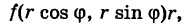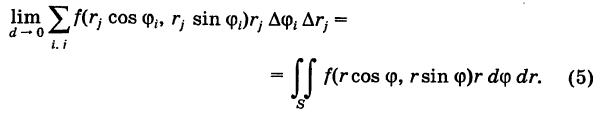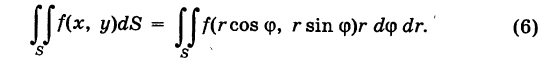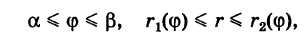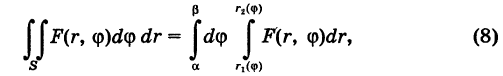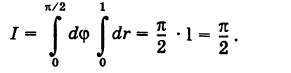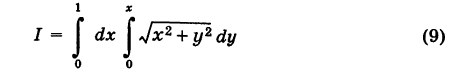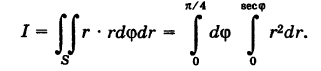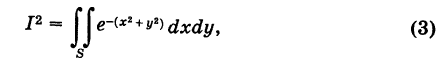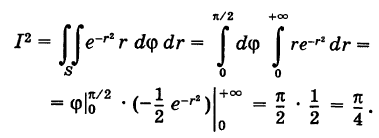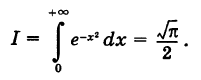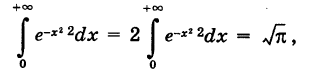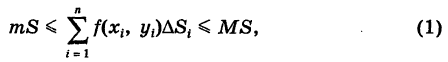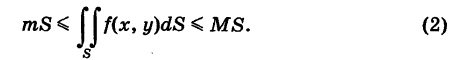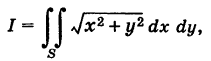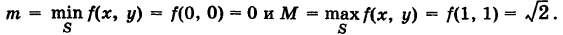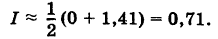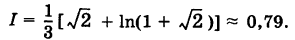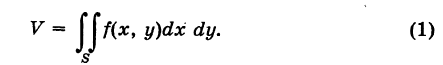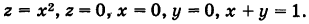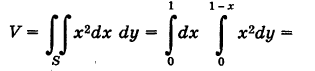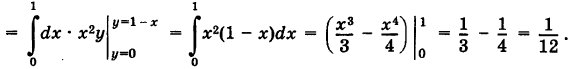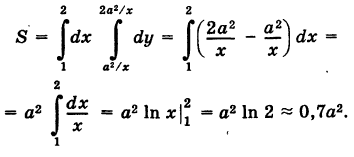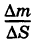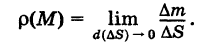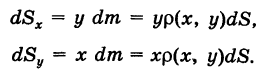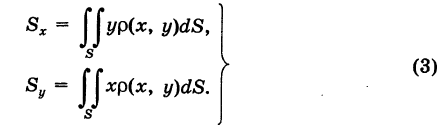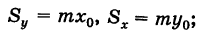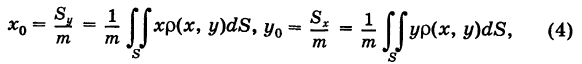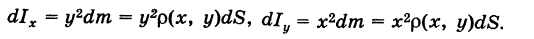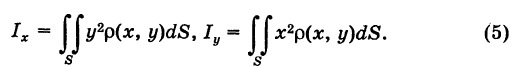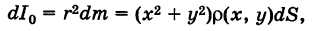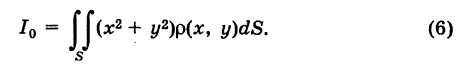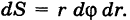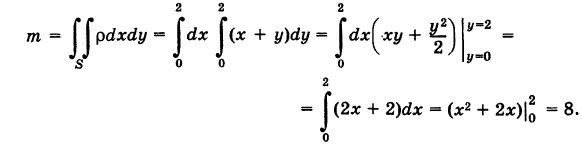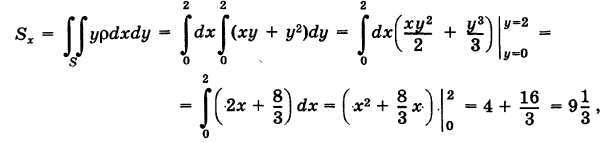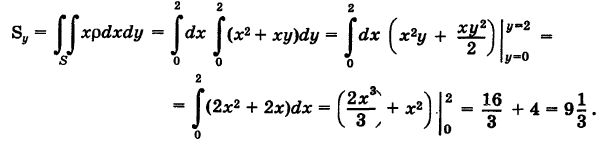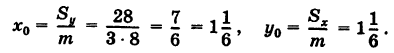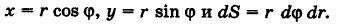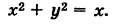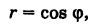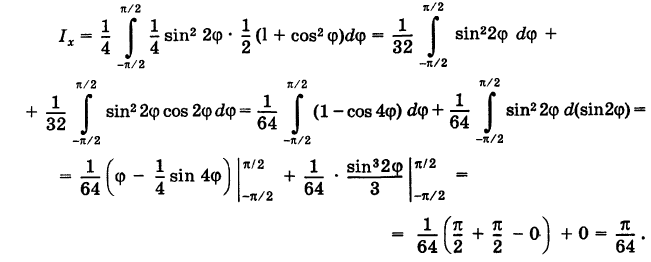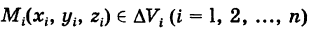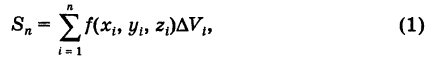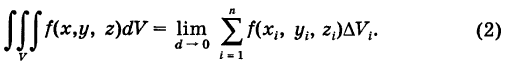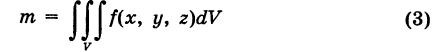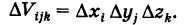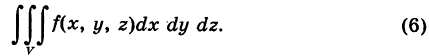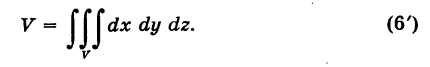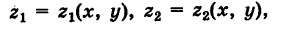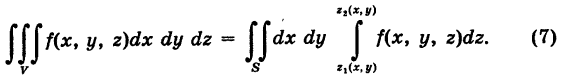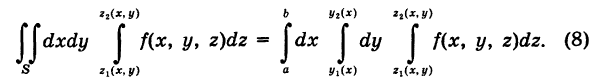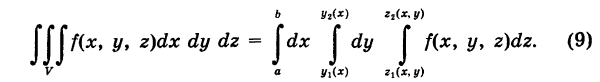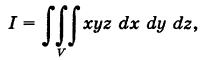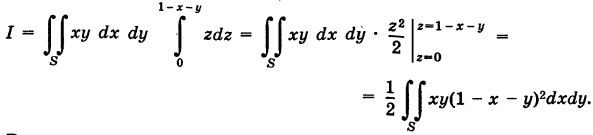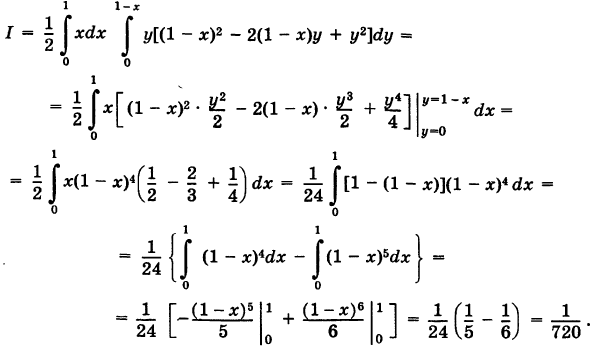двойной интеграл и его приложения
Двойной интеграл и его приложения
Двойной интеграл от функции \(f\left(
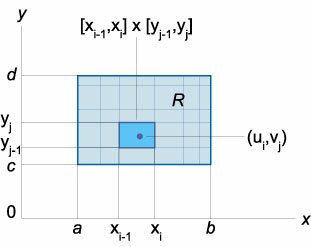
где прямоугольник \(\left[
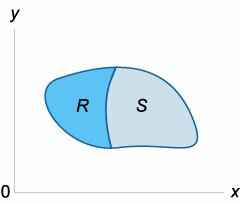
Двойной интеграл от суммы функций равен сумме интегралов от этих функций:
\(\large\iint\limits_R\normalsize <\left[
Постоянный коэффициент можно выносить за знак двойного интеграла:
\(\large\iint\limits_R\normalsize
Если \(f\left(
\(\large\iint\limits_R\normalsize
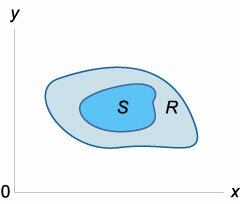
Если \(f\left(
\(\large\iint\limits_S\normalsize
Если \(f\left(
\(\large\iint\limits_
Здесь \(
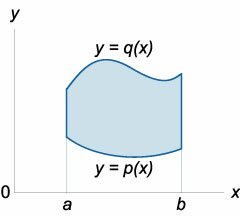
Повторный интеграл в области типа I
\(\large\iint\limits_R\normalsize
где область интегрирования \(R\) определяется неравенствами
\(R = \left\ < \left(
Повторный интеграл в области типа II
\(\large\iint\limits_R\normalsize
где область интегрирования \(R\) определяется неравенствами
\(R = \left\ < \left(
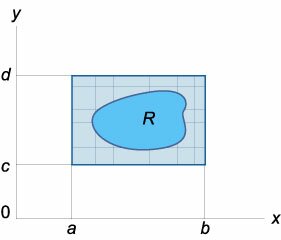
Двойной интеграл в прямоугольной области
Если \(R\) является прямоугольной областью \(\left[
\(\large\iint\limits_R\normalsize
В частном случае, когда подынтегральная функция \(f\left(
\(\large\iint\limits_R\normalsize
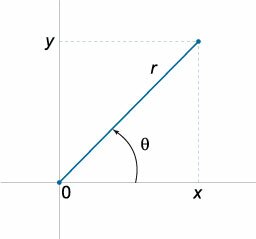
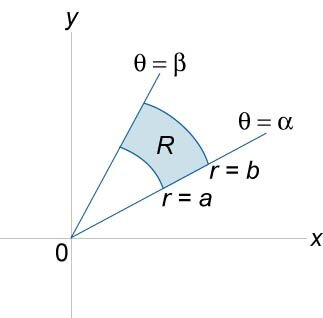
Полярные координаты
\(x = r\cos \theta, y = r\sin \theta \)
Двойной интеграл в полярных координатах
Дифференциал \(dxdy\) в полярных координатах определяется выражением
\(dxdy = \left| <\large\frac<<\partial \left(
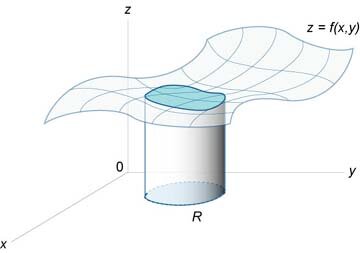
Объем тела
\(V = \large\iint\limits_R\normalsize
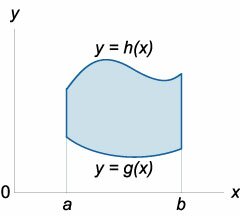
Если \(R\) является областью типа \(I\), ограниченная линиями \(x = a\), \(x = b\), \(y = h\left( x \right)\), \(y = g\left( x \right)\), то
\(V = \large\iint\limits_R\normalsize
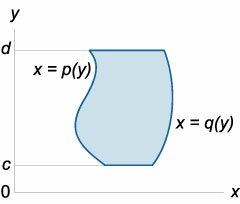
Если \(R\) является областью типа \(II\) и ограничена линиями \(y = c\), \(y = d\), \(x = q\left( y \right)\), \(x = p\left( y \right)\), то
\(V = \large\iint\limits_R\normalsize
Масса пластины
\(m = \large\iint\limits_R\normalsize <\rho \left(
Пластина расположена в области \(R\) и ее плотность в точке \( <\left(
Статические моменты пластины
Момент пластины относительно оси \(Ox\) определяется формулой
\(
Аналогично, момент пластины относительно оси \(Oy\) выражается в виде
\(
Моменты инерции пластины
Момент инерции пластины относительно оси \(Ox\) вычисляется по формуле
\(
Момент инерции пластины относительно оси \(Oy\) равен
\(
Полярный момент инерции определяется выражением
\(
Координаты центра масс пластины
\(\bar x = \large\frac<<
Заряд пластины
\(Q = \large\iint\limits_R\normalsize <\sigma \left(
где электрический заряд распределен по области \(R\) и его плотность в точке \( <\left(
Среднее значение функции
\(\mu = \large\frac<1>\iint\limits_R\normalsize
Двойной интеграл и его приложения
1. Вычисление объема тела
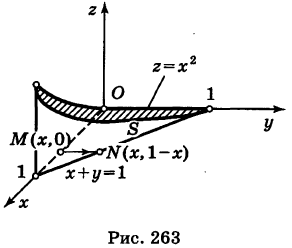
Пример 6.9. Вычислить объём тела, ограниченного параболоидом z = x 2 + y 2 + 1, плоскостью x + y –3=0 и координатными плоскостями.
Решение. Основанием тела служит треугольник ОАВ. Область D в данном случае определяется неравенствами:
2. Вычисление площади плоской фигуры
Если положить в формуле (6.18) f ( x , y )=1, то цилиндрическое тело «превратится» в прямой цилиндр с высотой h = 1. Объем такого цилиндра,
или, в полярных координатах,
Пример 6.10. Вычислить площадь фигуры, ограниченной прямой y = 2 x + 1 и параболой y = x 2 + 1.
Решение. Решая совместно систему
Применяя формулу (6.19), будем иметь:
Решение. Переходим к полярной системе координат, полагая x = r cos φ и y = r sin φ ; тогда получаем
3. Вычисление массы плоской фигуры (пластины)
Масса плоской пластинки D с переменной плотностью γ =γ ( x , y ) находится по формуле
4. Определение статических моментов и координат центра тяжести плоской фигуры
Статические моменты фигуры D относительно осей 0 x и 0 y могут быть вычислены по формулам
а координаты центра масс фигуры – по формулам
Статические моменты широко используются в сопротивлении материалов и других технических науках.
5. Определение моментов инерции плоской фигуры
Момент инерции фигуры относительно начала координат – по формуле
Находим статические моменты пластинки по формулам (6.22):
Находим координаты центра тяжести пластинки, используя формулы (6.23):
6. Поверхностный интеграл I рода
Теорема 6.3 (о существовании поверхностного интеграла). Если поверхность S гладкая (в каждой ее точке существует касательная плоскость, которая непрерывно меняется с перемещением точки по поверхности), а функция f ( x ; y ; z ) непрерывна на этой поверхности, то поверхностный интеграл существует
где D 1 и D 2 – проекции поверхности S на координатные плоскости xО z и y О z соответственно.
6.1. Площадь поверхности
Пример 6.14. Вычислить площадь части плоскости x + y + z = 4, вырезаемой цилиндром x 2 + y 2 = 4 (рис. 6.10).
– данную область разбивают на конечное число мелких частей;
– делают для каждой такой части предположения, упрощающие задачу;
– находят приближенное значение искомой величины;
– переходят к пределу при неограниченном измельчении разбиения области.
Проиллюстрируем описанный способ на примере определения массы материальной поверхности.
6.2. Масса поверхности
6.3. Моменты и центр тяжести поверхности. С татические моменты, координаты центра тяжести, моменты инерции материальной поверхности S находятся по соответствующим формулам:
Двойной интеграл и его приложения
Эта сумма называется интегральной суммой для функции f ( x , y ) в области D . Если f ≥ 0 в области D , то каждое слагаемое 
Рассмотрим произвольную последовательность интегральных сумм, составленных с помощью функции f ( x , y ) для данной области D :
Область D при этом называется областью интегрирования.
1. Вычисление двойного интеграла в декартовой система координат
Рассмотрим область D , лежащую в плоскости x 0 y и являющуюся правильной в направлении оси 0 y . Это означает, что всякая прямая, параллельная оси 0 y и проходящая через внутреннюю точку области, пересекает границу области в двух точках N 1 и N 2.
Если область D является правильной как в направлении оси 0 x , так и в направлении оси 0 y , то она называется просто правильной областью.
Пусть функция f ( x , y ) непрерывна в области D . Рассмотрим выражение
которое назовем двукратным интегралом от функции f ( x , y ) по области D . В этом выражении сначала вычисляется внутренний интеграл, стоящий в скобках, причем интегрирование производится по y , а x считается постоянной величиной. В результате интегрирования получится непрерывная функция от x :

Эту функцию мы интегрируем по x в пределах от a до b :
В результате получается некоторое постоянное число.
Теорема 6.2. Двойной интеграл от непрерывной функции f ( x , y ) по правильной области D равен двукратному интегралу от этой функции по области, то есть
Очевидно, что в этом случае
Решение. Применим формулу (6.5), считая внутренний интеграл по переменной y :
Если область D является правильной в направлении обеих осей координат, то применимы обе формулы (6.5) и (6.6), следовательно,
Таким образом, повторное интегрирование не зависит от порядка интегрирования. Поэтому при вычислении двойного интеграла следует пользоваться той из двух формул, которая приводит к менее трудоемким выкладкам. Полезно для упражнения в вычислении повторного интегрирования рассматривать задачу о замене порядка интегрирования в двойном интеграле 
Аналогичные выкладки производят при необходимости замены порядка интегрирования в двойном интеграле :
Примечание. В случае, когда какая-либо из этих границ состоит из двух или большего числа линий, записанных разными уравнениями, то область D разбивается на части, а интеграл – на сумму интегралов по этим частям
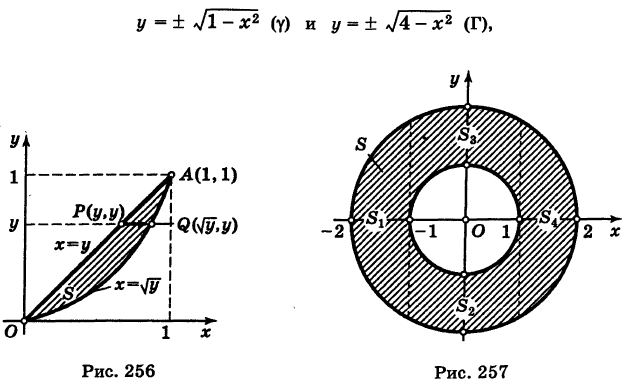
Пример 6.2. Изменить порядок интегрирования 
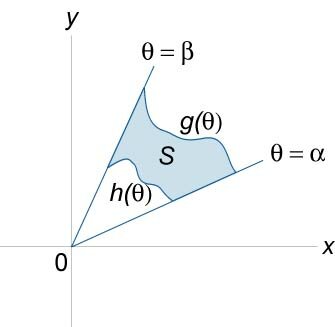
2. Вычисление двойного интеграла в полярной системе координат
Для вычисления такого двойного интеграла применяют то же правило сведения его к двукратному интегралу. Так, если область D имеет вид, изображенный на рисунке 6.2 (ограничена лучами φ=α и φ=β, где α β, и кривыми 
Переходя к полярной системе координат с помощью (6.8), получаем:
Содержание:
Двойные и тройные интегралы
Понятие двойного интеграла
В теории определенного интеграла для нахождения площади криволинейной трапеции было введено понятие интегральной суммы, пределом которой является определенный интеграл. На основе задачи об определении объема тела мы придем к понятию двумерной интегральной суммы, предел которой называется двойным интегралом.
Пример:
Найти объем тела, ограниченного сверху непрерывной поверхностью z = f(x, у) (f(x, у)
Тело указанного вида для краткости называется цилиндроидом. В частном случае, когда верхнее основание цилиндроида есть плоскость, параллельная нижнему основанию его, то цилиндроид называется цилиндром. Примером цилиндра служит круговой цилиндр, рассматриваемый в средней школе. Обобщая рассуждение, обычно применяемое для нахождения объема кругового цилиндра, нетрудно доказать, что объем V цилиндра с площадью основания S и высотой Н равен V = SH.
Для вычисления объема V данного цилиндроида разобьем основание его S на конечное число элементарных ячеек 
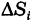
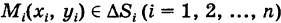
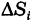
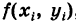
Объем такого столбика на основании формулы объема цилиндра, очевидно, равен
где 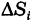
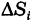
Формула (2) дает возможность найти объем V с любой степенью точности, если число ячеек 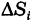
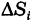
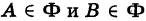
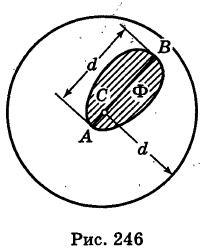
Из данного определения следует, что фигура Ф, имеющая диаметр d, целиком помещается внутри круга радиуса d, описанного из любой ее точки С как из центра. Поэтому если 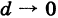
— наибольший из диаметров ячеек 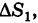
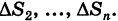
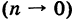
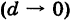
Здесь мы для удобства ячейки и их площади обозначаем одинаковыми буквами. Разница между ними видна из контекста.
Ячейки 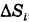
Точнее говоря, по определению под объемом цилиндроида понимается предел (3), если он существует.
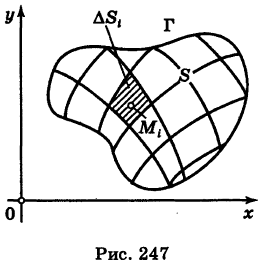
Выражение, стоящее в правой части формулы (3), называется двойным интегралом от функции f(x, у), распространенным на область S, и обозначается следующим образом:
Поэтому для объема цилиндроида окончательно имеем
Обобщая конструкцию, примененную для вычисления объема цилиндроида, приходим к следующим определениям.
Определение: Двумерной интегральной суммой (2) от данной функции f(x9 у)> распространенной на данную область S, называется сумма парных произведений площадей элементарных ячеек 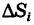
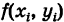
Определение: Двойным интегралом (4) от функции f(x, у), распространенным на данную область S, называется предел соответствующей двумерной интегральной суммы (2) при неограниченном возрастании числа п элементарных ячеек 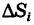
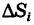
В формуле (4) у) называется подынтегральной функцией, S — областью интегрирования, a dS — элементом площади. Справедлива следующая теорема:
Теорема: Если область S с кусочно-гладкой границей Г ограничена и замкнута, а функция f(x, у) непрерывна в области S, то двойной интеграл
существует, т. е. предел соответствующей двумерной интегральной суммы существует и не зависит от способа дробления области S на элементарные ячейки 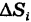
В дальнейшем мы будем предполагать, что условия этой теоремы выполнены.
В формуле (6) нет необходимости указывать, что 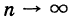
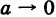
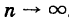
Если f(x, у) 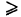
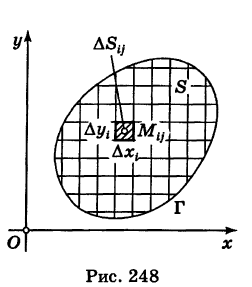
Так как значение двойного интеграла не зависит от вида элементарных ячеек, то в дальнейшем при решении задач мы будем использовать это обстоятельство, выбирая наиболее подходящие сетки. Весьма часто удобной оказывается прямоугольная сетка, образованная пересечением двух систем прямых, параллельных соответственно координатным осям Ох и Оу (рис. 248). В этом случае элементарными ячейками 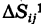
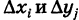
Чтобы подчеркнуть использование прямоугольной сетки, в обозначении интеграла (4) полагают
(двумерный элемент площади в прямоугольных координатах), причем
где 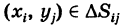
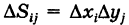
В следующих параграфах мы рассмотрим основные способы вычисления двойного интеграла.
Здесь мы применяем двойную индексацию ячеек, указывая отдельно номер i вертикальной полосы и номер j горизонтальной полосы, содержащих данную ячейку, подобно тому, как на билете в кино отмечается номер ряда и номер места.
Двойной интеграл в прямоугольных декартовых координатах
Предположим для определенности, что область интегрирования S представляет собой криволинейную трапецию (рис. 249);
Пример:
Расставить пределы интегрирования в двойном интеграле
если область интегрирования 5 есть круговое кольцо, ограниченное окружностями 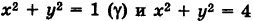
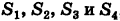
Аналогичная формула получится, если мы будем расставлять пределы интегрирования в другом порядке.
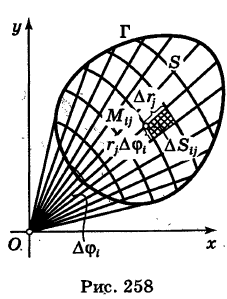
Двойной интеграл в полярных координатах
Пусть в двойном интеграле
при обычных предположениях мы желаем перейти к полярным координатам г и ф, полагая
Область интегрирования S разобьем на элементарные ячейки 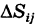
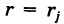
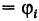
Так как окружность перпендикулярна (ортогональна) радиусам, то внутренние ячейки 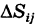
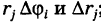
Что касается ячеек AS^ неправильной формы, примыкающих к границе Г
области интегрирования S, то эти ячейки не повлияют на значение двойного интеграла и мы их будем игнорировать.
В качестве точки 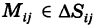
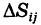
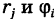
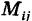
Двойной интеграл (1) представляет собой предел двумерной интегральной суммы, причем можно показать, что на значение этого предела не влияют добавки к слагаемым интегральной суммы, являющиеся бесконечно малыми высшего порядка малости. Поэтому, учитывая формулы (3) и (3′), получаем
где d — максимальный диаметр ячеек 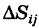
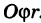
соответствующая прямоугольной сетке с линейными элементами 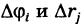
Выравнивая формулы (4) и (5), получаем окончательно
называется двумерным элементом площади в полярных координатах. Итак, чтобы в двойном интеграле (1) перейти к полярным координатам, достаточно координаты х и у заменить по формулам (2), а вместо элемента площади dS подставить выражение (7).
Для вычисления двойного интеграла (6) его нужно заменить повторным. Пусть область интегрирования S определяется неравенствами
где 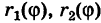
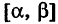
Пример:
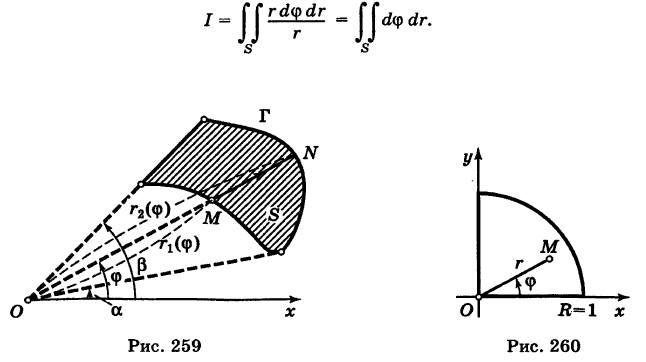
Переходя к полярным координатам 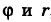
где S — первая четверть круга радиуса R = 1 с центром в точке О (0, 0) (рис. 260).
Так как 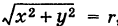
Область S определяется неравенствами 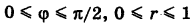
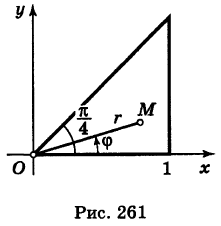
Пример:
перейти к полярным координатам.
Область интегрирования здесь есть треугольник S, ограниченный прямыми у=0, у = х, х = 1 (рис. 261).
В полярных координатах уравнения этих прямых записываются следующим образом: 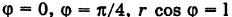
Отсюда на основании формул (6) и (8), учитывая, что 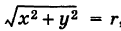
Интеграл Эйлера—Пуассона
С помощью полярных координат можно просто вычислить важный для теории вероятностей интеграл Эйлера— Пуассона
Так как определенный интеграл не зависит от обозначения переменной интегрирования, то, очевидно, можно также записать
Перемножая формулы (1) и (2) и учитывая, что произведение этих однократных интегралов можно рассматривать как двойной интеграл от произведения подынтегральных функций, будем иметь
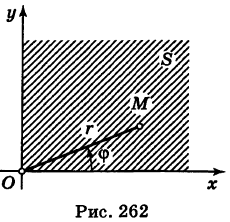
где область S определяется неравенствами
и, следовательно, представляет собой первый квадрант координатной плоскости Оху (рис. 262).
Переходя в интеграле (3) к полярным координатам, получим
Отсюда, учитывая положительность числа 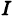
В силу четности функции 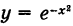
что представляет собой площадь, ограниченную осью Ох и кривой Гаусса 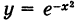
Теорема о среднем
Пусть функция f(x, у) непрерывна в ограниченной замкнутой области 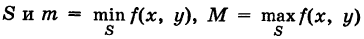
Для двумерной интегральной суммы этой функции, распространенной на область S, имеем оценки
где 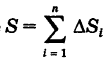
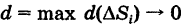
называется средним значением функции 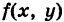
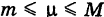
Формулу (3) можно переписать в следующем виде:
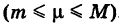
Не нужно думать, что формула (4) дает универсальный способ вычисления двойного интеграла. Дело в том, что, как правило, среднее значение функции определяется через двойной интеграл. Поэтому реальный смысл здесь имеет оценка (2).
Пример:
где S — квадрат
Для функции f(x, у) = 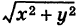
Так как S = 1, то 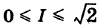
Эта оценка грубая, так как точное значение интеграла есть
Более точное значение интеграла I получится, если область интегрирования S разбить на достаточно мелкие части и к каждой из них применить теорему о среднем.
Геометрические приложения двойного интеграла
Прямой цилиндроид, построенный на основании S в координатной плоскости Оху и ограниченный сверху непрерывной поверхностью z = f(x, у), имеет объем, равный
Пример:
Найти объем 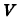
Решение:
Искомое тело имеет своим основанием треугольник S на плоскости Оху у образованный линиями 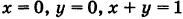
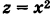
Если в формуле (1) положить
то получим объем прямого цилиндра с высотой 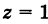
Формулу (2) можно записать также в виде
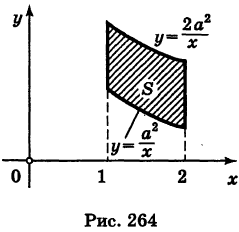
Пример:
Найти площадь, ограниченную гиперболами 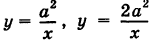
Решение:
На основании формулы (2) получим, что площадь S равна
Физические приложения двойного интеграла
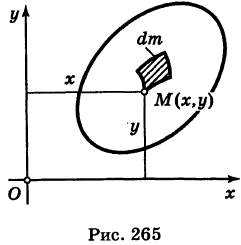
Пусть S — материальная пластинка. Если 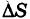
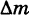
называется средней поверхностной плотностью куска 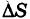
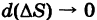
Очевидно, поверхностная плотность р(М) пластинки S есть функция точки М. Понятия средней поверхностной плотности пластинки и поверхностной плотности пластинки в данной точке
вполне аналогичны понятиям средней линейной плотности дуги и линейной плотности дуги в точке, введенным.
Положим, что поверхностная плотность пластинки S в текущей точке М(х, у) равна 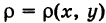
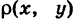
Интегрируя выражение (1) по всей пластинке S, находим массу пластинки
Рассматривая dm как материальную точку, удаленную от осей координат Ох и Оу на расстояния у их, получим элементарные статические моменты пластинки
Отсюда, интегрируя эти выражения по всей пластинке S, находим статические моменты пластинки S относительно координатных осей
В механике доказывается, что статический момент пластинки относительно какой-нибудь оси совпадает со статическим моментом точечной массы, равной массе пластинки, сосредоточенной в центре масс ее относительно той же оси (теорема Вариньона). Отсюда, обозначая через (х0, у0) координаты центра масс пластинки S, будем иметь
где 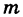
Аналогично, для элементарных моментов инерции пластинки S относительно осей координат Ох и Оу получаем выражения
Отсюда после интегрирования по пластинке S будем иметь моменты инерции пластинки S относительно координатных осей
Элементарный полярный момент инерции определяется формулой
где 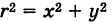
Из формул (5) и (6) следует, что
Полагая 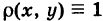
Пример:
Определить координаты центра масс квадратной пластинки S: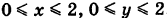
Решение:
Пользуясь формулой (2), находим массу пластинки
По формуле (3) определяем статические моменты пластинки S относительно координатных осей:
Равенство моментов 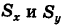
На основании формул (4) центр масс пластинки S имеет координаты
Пример:
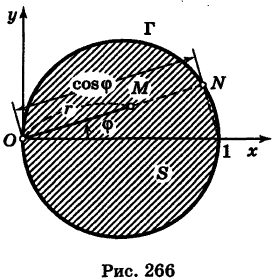
Найти момент инерции 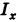
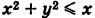
Решение:
Полагая р = 1, на основании первой формулы (5) имеем
Задачу будем решать в полярных координатах. Имеем
Уравнение границы Г области S есть
Отсюда, переходя к полярным координатам, получаем 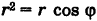
причем так как 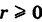
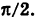
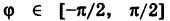
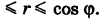
Как известно, 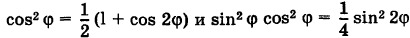
Понятие о тройном интеграле
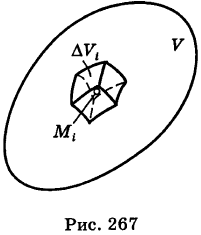
По аналогии с двойным интегралом определяется так называемый тройной интеграл. Пусть в декартовом пространстве Охуz задана конечная замкнутая область V и f(x, у, z) — ограниченная функция, определенная в V. Разобьем область V на конечное число ячеек 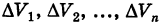
где 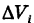
Обозначим через d наибольший из диаметров ячеек 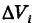
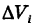
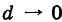
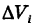
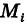
от функции 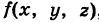
Доказывается, что если подынтегральная функция 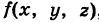
Если область V заполнена массой и 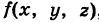
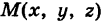
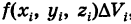
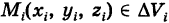
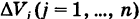
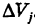
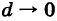
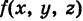
представляет собой массу, заполняющую область интегрирования V. В частности, если плотность f(x, у, z) 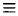
Если вычисление тройного интеграла (2) ведется в прямоугольных координатах х, у, z, то в качестве ячеек 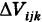
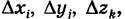
В этом случае элемент объема dV считают равным
(элемент объема в прямоугольных координатах) и тройной интеграл (2) записывают в следующем виде:
В частности, для объема тела получаем формулу
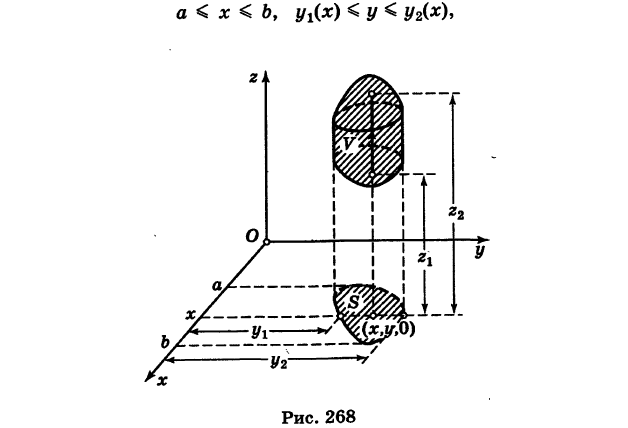
В простейшем случае вычисление тройного интеграла (6) сводится к трем квадратурам. А именно, пусть область интегрирования Г стандартна относительно оси Oz, т. е. ограничена снизу и сверху соответственно однозначными непрерывными поверхностями
причем проекция области V на координатную плоскость Оху есть плоская область S (рис. 268).
Отсюда следует, что при фиксированных значениях (х, у) 6 S соответствующие аппликаты z точек области V изменяются в пределах 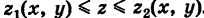
Если, кроме того, проекция S стандартна относительно оси Оу и определяется неравенствами
где 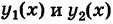
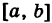
Из формул (7) и (8) получаем окончательно
Таким образом, вычисление тройного интеграла сводится к трем квадратурам.
Заметим, что если область интегрирования V стандартна относительно всех трех координатных осей Ох, Оу и Oz, то пределы интегрирования для тройного интеграла (6) можно расставить 3! = 6 различными способами.
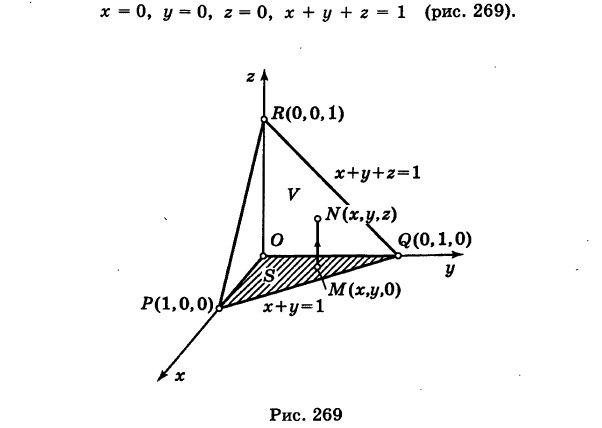
Пример:
где V — пирамида OPQR, ограниченная следующими плоскостями:
Решение:
Проекция области V на координатную плоскость Оху есть треугольник S, ограниченный прямыми
При 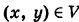
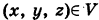
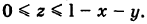
Расставляя пределы интегрирования для треугольника S, получаем
Число I представляет собой массу пирамиды V, если плотность ее в текущей точке 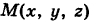
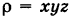
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.