индуктивная проводимость чему равна

Индуктивная проводимость чему равна

Характеристики простейших пассивных двухполюсников в цепях синусоидального тока

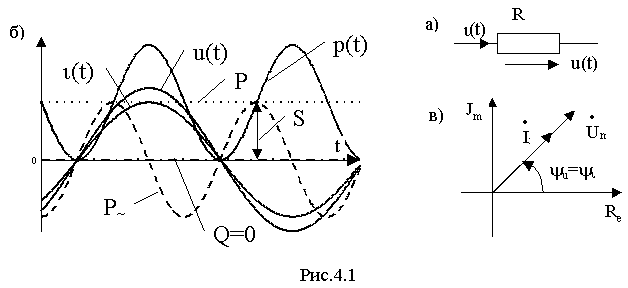
Поскольку мгновенные значения напряжения и тока для резистивного элемента связаны законом Ома, то i (t)= u(t)/ R= (U m / R) Sin ( w t+ y u )

а) при синусоидальном напряжении на резистивном элементе ток в нем также синусоидален;

в) амплитуда и действующее значение тока равны соответствующим значениям напряжения, деленным на R.

Мгновенная мощность в резистивном элементе определяется формулой

p(t)=u(t) i (t)=UI- UICos2 w t=p = +p

и иллюстрируется графиком на рис.4.1,б. Мощность пульсирует от нулевого значения до максимального, принимая только положительные значения. Это означает, что при любом направлении тока энергия поступает от источника в резистивный элемент и рассеивается в нем в виде тепла.

Средняя за период переменного тока (или активная) мощность равна

Р= p = = UI=I 2 R=U 2 g, Вт.

Поскольку j =0, то реактивная мощность равна 0, т.е. Q = UISin j =0.

Полная мощность равна активной мощности, т.е. S=UI.

Z R =.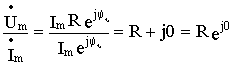

а) комплексное сопротивление резистивного элемента содержит только активную составляющую ( реактивная составляющая равна нулю), т.е.

;

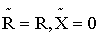
б) полное сопротивление резистивного элемента z=R;

Комплексная проводимость резистивного элемента есть величина обратная комплексному сопротивлению, т.е.

Y R =1/ Z R = (1/R)e j0 =1/R, Сим.

а) комплексная проводимость резистивного элемента содержит только активную составляющую

;

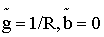
б) полная проводимость резистивного элемента y=1/R;

в) аргумент комплексной проводимости равен 0 ( j =0).

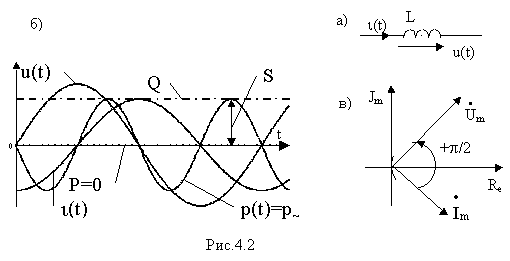
Пусть ток в индуктивном элементе с индуктивностью L (рис. 4.2а,б) синусоидален, т.е. i (t)= I m Sin ( w t+ y i ).

Поскольку мгновенные значения напряжения на индуктивном элементе пропорционально скорости изменения тока, то

u(t)=L d i /dt= I m w L Cos ( w t+ y i )= I m w L Sin ( w t+ y i + p /2)

или u(t)=U m Sin ( w t+ y u ), где U m =I m w L –амплитуда напряжения и y u = y i + p /2- начальная фаза напряжения.

а) при синусоидальном токе в индуктивном элементе напряжение на нем также синусоидально;

б) напряжение опережает по фазе ток на угол j = p /2 (рис.4.2,б);

в) амплитуда и действующее значение напряжения равны соответствующим значениям тока, умноженным на величину

называемую индуктивным сопротивлением.

Как видно, при неизменной амплитуде напряжения на индуктивном элементе с ростом частоты пропорционально падает амплитуда тока. Фазовый сдвиг между напряжением и током при всех частотах остается неизменным и равным p /2.

Мгновенная мощность в индуктивном элементе определяется формулой

p(t)=u(t) i (t)=UISin2( w t+ y i )=p

Средняя за период переменного тока (или активная) мощность для индуктивного элемента равна нулю, т.е. Р= UICos( p /2)=0.

Поскольку j = p /2, то реактивная мощность положительна и равна

Полная мощность равна по величине реактивной мощности, т.е. S=UI.

Z L = 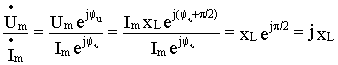, Ом

а) комплексное сопротивление индуктивного элемента содержит только реактивную составляющую ( активная составляющая равна нулю)., т.е. ;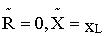

б) полное сопротивление резистивного элемента z=x L ;

в) аргумент комплексного сопротивления равен p /2 ( j = p /2) и потому вектор напряжения на индуктивном элементе опережает вектор тока в нем на p /2 ( рис. 4.2,в ) ;

Комплексная проводимость индуктивного элемента есть величина обратная комплексному сопротивлению, т.е.

а) комплексная проводимость индуктивного элемента содержит только реактивную составляющую

;

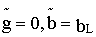
б) полная проводимость индуктивного элемента y=b L ;

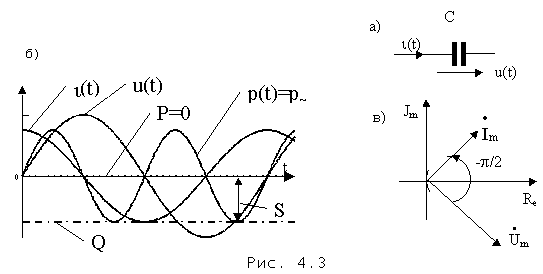
Пусть напряжение на емкостном элементе с емкостью С (рис. 4.3а,б) синусоидально, т.е. u(t)= U m Sin ( w t+ y u ).

Поскольку мгновенное значения тока в емкостном элементе пропорционально скорости изменения напряжения, то

i (t)=С du /dt= U m w C Cos ( w t+ y u )= U m w C Sin ( w t+ y u + p /2)

или i (t)= I m Sin ( w t+ y i ), где I m = U m w С –амплитуда тока и y i = y u + p /2)- начальная фаза тока.

а) при синусоидальном напряжении на емкостном элементе ток в нем также синусоидален;

в) амплитуда и действующее значение тока равны соответствующим значениям напряжения, умноженным на величину

называемую емкостным сопротивлением.

Мгновенная мощность в емкостном элементе определяется формулами

p(t)=u(t) i (t)=UISin2( w t+ y u )=p

Средняя за период переменного тока (или активная) мощность для емкостного элемента равна нулю, т.е.

Полная мощность по величине равна реактивной мощности, т.е.

Z с = 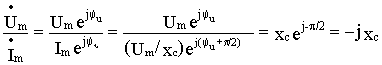, Ом

а) комплексное сопротивление емкостного элемента содержит только реактивную составляющую ( активная составляющая равна нулю). Таким образом для емкостного элемента

;

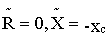
б) полное сопротивление емкостного элемента z=x с ;

Комплексная проводимость емкостного элемента есть величина обратная комплексному сопротивлению, т.е.

а) комплексная проводимость емкостного элемента содержит только реактивную составляющую

;

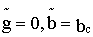
б) полная проводимость индуктивного элемента y=b с ;

Поскольку комплексные сопротивления и проводимости индуктивного и емкостного элементов содержат только реактивные составляющие, в литературе эти элементы часто называют реактивными элементами. Резистивный элемент, комплексное сопротивление и проводимость которого содержат только активные составляющие, называют активным сопротивлением.

Источник

Краткие теоретические сведения

В работе исследуется цепь переменного тока, состоящая из параллельно включенных индуктивной катушки и батареи конденсаторов (резонансный контур) (рис.10).

Рис.15. Цепь переменного тока с параллельным соединением катушки индуктивности и конденсаторной батареи

При параллельном соединении электроприемников на каждую ветвь цепи подается одно и то же напряжение, равное напряжению, приложенному к зажимам цепи.

Для схемы, представленной на рис.15, имеем

где U – напряжение, приложенное к зажимам цепи;

U_К – напряжение, приложенное к катушке индуктивности;

U_С – напряжение, приложенное к конденсаторной батарее.

Ток I в неразветвленной части такой цепи определяется как геометрическая сумма токов катушки I_К и конденсатора I_С, причем ток катушки в свою очередь является геометрической суммой активного I_R и индуктивного I_L токов.

I = = U∙ (23)

g_K = ; (24)

b_L = ; (25)

b_C = = ; (26)

Y = , (27)

где Y – полная проводимость цепи, См.

Формула (23) представляет собой выражение закона Ома для цепи переменного тока с параллельным соединением катушки (g_K и b_L) и конденсатора (b_C). В общем случае при наличии нескольких ветвей с активными, индуктивными и емкостными проводимостями выражение закона Ома для параллельной цепи переменного тока примет вид

I = U ∙ Y = U ∙

Ток, протекающий в индуктивной катушке

I_К = U∙ (28)

ток, протекающий через конденсатор

I_С = = U ∙ b_C . (29)

Активная мощность, выделяемая в цепи

Р = . (30)

Векторная диаграмма, представленная на рис.16б аналогична векторной диаграмме цепи переменного тока с активным сопротивлением в том смысле, что векторы напряжения U = U_K = U_С и тока I в неразветвленной части цепи совпадают по фазе, угол сдвига межу ними φ=0 и коэффициент мощности cos φ = 1. В этом случае ток I в неразветвленной части цепи будет иметь минимально возможное значение при данной величине приложенного напряжения. Из выражения (23) при I_L = I_С получаем

Отсутствие влияния реактивных токов на величину тока в неразветвленной части цепи в этом случае объясняется тем, что равные между собой и смещенные относительно друг друга по фазе на 180º токи I_L и I_С взаимно компенсируются.

Режим работы, устанавливающийся в цепи переменного тока с параллельным соединением катушки и конденсатора в случае, когда индуктивная проводимость катушки (первой ветви) равна емкостной проводимости конденсатора (второй ветви) называется резонансом токов.

Сущность явления резонанса токов заключается в том, что ток в неразветвленной части цепи (общий ток) уменьшается до минимально возможного значения, а по катушке и конденсатору (ветвям цепи) протекают реактивные токи I_L и I_С, которые могут в несколько раз превышать общий ток I.

Для резонанса напряжений (см. лаб.работу №2) было получено выражение (22) для определения резонансной частоты f_Р при заданных величинах индуктивности катушки L и емкости конденсатора С.

f_Р = (32)

Общую формулу для расчета резонансной частоты любой параллельной цепи переменного тока из условия b_L = b_С получить нельзя, т.к. в выражения (25) и (26) для b_L = b_С входят полные сопротивления ветвей цепи (Z_K = Z_С ), которые выражаются различными формулами в зависимости от того, какие сопротивления (активные, индуктивные, емкостные) входят в ту или иную цепь. Для цепи, представленной на рис.14 имеем

= = = , откуда

= ωС (33)

Из выражения (33) получаем формулу для расчета резонансной угловой частоты

ω_Р = . (34)

Если рассматривать идеальную катушку индуктивности, в которой индуктивное сопротивление много больше активного Х_L >> R_K, то последним можно пренебречь, т.е. считать R_K =0.

Тогда из выражения (34) получаем

ω_Р = , рад/с; f_Р = , Гц (35)

Таким образом, для простейшей электрической цепи, содержащей по одному элементу в каждой ветви (рис.17) условие резонанса токов b_L = b_С превращается в условие Х_L = Х_С , такое же как и условие резонанса напряжений для последовательной цепи переменного тока.

Рис.17. простейшая параллельная LC–цепь переменного тока

Действительно, для цепи, представленной на рис.14

b_L = ; b_C =

Резонанс токов может быть получен изменением угловой частоты переменного тока ω, индуктивности L или емкости С. В данной работе резонанс токов получают путем изменения величины емкости С.

При увеличении емкости конденсаторной батареи емкостное сопротивление Х_С = будет уменьшаться, а емкостная проводимость b_C = = ωС увеличивается. Если подобрать значения индуктивности катушки L и начальной емкости конденсаторной батареи таким образом, чтобы b_L было больше, чем b_C0, то при увеличении емкости общая проводимость цепи Y в соответствии с выражение (27) будет уменьшаться, до того момента, когда b_C станет равным b_L, а затем начнет возрастать. При этом ток в цепи в соответствии с выражением (23) будет уменьшаться при b_L > b_С, достигнет минимума при b_L = b_С, а затем начнет увеличиваться. Резонансу токов будет соответствовать значение емкости конденсаторной батареи С_Р, при котором ток I минимален (рис.18).

Рис.18. Получение резонанса токов

Определение параметров цепи переменного тока с параллельным соединением катушки и конденсатора осуществляется следующим образом.

При заданном значении напряжения, приложенного к зажимам цепи U и при каждом из заданных значений емкости конденсаторной батареи С измеряются величины токов неразветвленной части цепи I, катушки I_К и конденсатора I_С, а также активной мощности цепи Р. Остальные параметры являются расчетными величинами.

Полная мощность цепи S = I ∙ U, ВА.

Коэффициент мощности цепи cos φ = .

Угол сдвига фаз между током и напряжением φ = arcos , град.

Индуктивная составляющая тока I_L = , A.

Полное сопротивление катушки Z_K = , Ом.

Активное сопротивление катушки R_K = , Ом.

Индуктивное сопротивление катушки Х_L = , Ом.

Активная проводимость катушки g_K = , Cм.

Индуктивная проводимость катушки b_L = , Cм.

Реактивная (индуктивная) мощность катушки Q_L = I_K 2 ∙ Х_L, ВАр.

Емкостное (полное) сопротивление конденсатора b_L = , Cм.

Реактивная (емкостная) мощность конденсатора Q_С = I_С 2 ∙ Х_С, ВАр.

Общая (эквивалентная проводимость) Y = , Ом.

ПЛАН РАБОТЫ.

Задание 1. Исследовать цепь переменного тока с параллельным соединением катушки и конденсатора при резонансе токов.

1. Собрать электрическую схему (рис.19).

Рис.19. Схема цепи переменного тока с параллельным соединением катушки и конденсатора

1. АТ – лабораторный автотрансформатор (ЛАТР).

4. W – ваттметр U = 75-150-300-600 В, I = 1-2 A.

6. Батарея конденсаторов С=32 мкФ (установлена на стенде).

2. Установить с помощью ЛАТРа напряжение на выходе U_вых = 50 В.

3. Измерить токи с помощью амперметров A₁ (I_ОБЩ), A₂ (I_КАТ), A₃ (I_КОНД), мощности P и напряжения U_ВЫХ, изменяя емкость батареи конденсаторов от 12 до 32 мкФ в следующем порядке: 12, 14, 16, 18, 20, 21, 22, 23, 24, 26, 28, 30, 32 мкФ.

4. Рассчитать параметры параллельной цепи переменного тока, указанные в табл.6.

5. Результаты измерений и вычислений внести в табл. 6.

7. Построить векторные диаграммы цепи переменного тока, соответствующие значениям емкости С = 16 мкФ, С = 26 мкФ и С = С_Р (резонанс токов).

Содержание отчета

1. Электрическая схема измерений с обозначениями приборов.

2. Расчет параметров параллельной цепи переменного тока.

3. Таблица измеренных и вычисленных величин.

5. Векторные диаграммы.

Таблица 6а. Измеренные величины

CII кI cPмкФАААВт1120,160,320,1852140,140,320,2153160,120,320,2354180,110,320,2755200,090,320,2956210,0950,320,3157220,0950,320,3358230,100,320,3559240,1050,320,36510260,110,320,38511280,140,320,42512300,1550,320,44513320,180,320,495

Таблица 6б. Вычисленные величины

CYb_Lb_CI_RI_LSQ_LQ_CQcos φφмкФCмCмCмААВАВАрВАрВАр––112214……1432

Контрольные вопросы

1. Какую мощность (полную, активную, реактивную, индуктивную, емкостную) измеряет ваттметр?

2. Как связано напряжение на зажимах цепи с напряжениями на катушке и конденсаторе при их параллельном соединении?

3. Что такое активная проводимость ветви параллельной цепи переменного тока?

4. Как определить индуктивную проводимость катушки?

5. Сформулируйте закон Ома для параллельной цепи переменного тока.

6. Как изменяется емкостная проводимость при увеличении емкости конденсатора?

7. При каком соотношении емкостного и индуктивного токов в параллельной цепи ток в неразветвленной части будет наименьшим?

8. При каком соотношении емкостного и индуктивного токов в параллельной цепи коэффициент мощности цепи будет равен единице?

9. Почему режим работы параллельной цепи, когда коэффициент мощности равен единице, называется резонансом токов?

10. В каких параллельных цепях переменного тока условие резонанса токов b_L = b_С может быть заменено условием Х_L = Х_С?

11. Как меняются показания ваттметра при увеличении емкости конденсатора?

12. Почему явление, при котором в неразветвленной части параллельной цепи ток минимален называется резонансом токов?

13. Как зависит величина тока, протекающего через конденсатор от его емкости?

14. Какова величина сдвига фаз между индуктивным и емкостным токами при резонансе токов?

15. В каких параллельных цепях переменного тока резонансная частота может быть определена по формуле f_Р = ?

16. Какие способы получения резонанса токов вы знаете?

17. Как должны быть соединены катушка и конденсатор, чтобы в цепи мог возникнуть резонанс токов?

18. Какой вектор принимается базисным при построении векторных диаграмм параллельной цепи переменного тока и почему?

19. Как графически определить ток в неразветвленной части параллельной цепи переменного тока, если известны величины токов в отдельных ветвях и значения коэффициентов мощности отдельных ветвей?

20. Что общего между явлениями резонанса токов и резонанса напряжений с энергетической точки зрения?

Источник