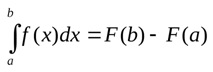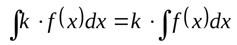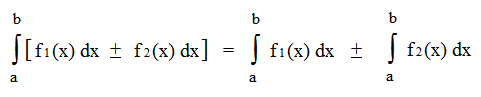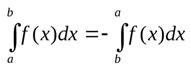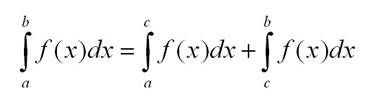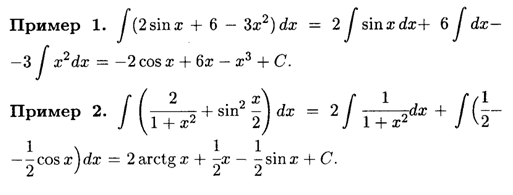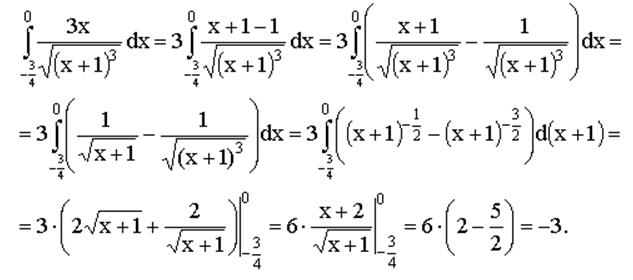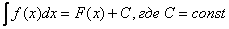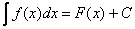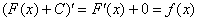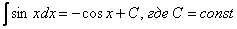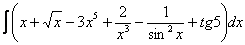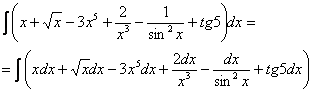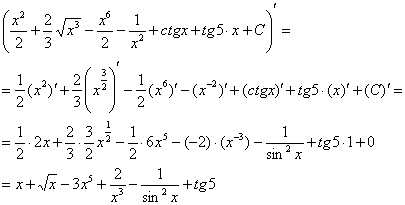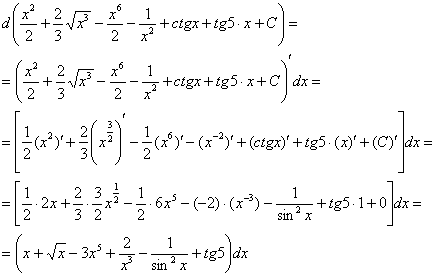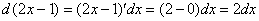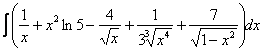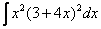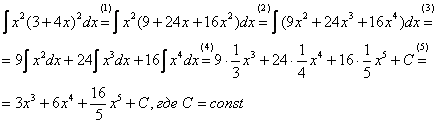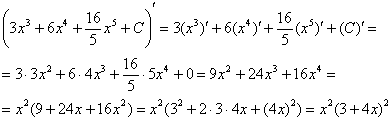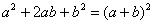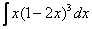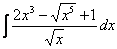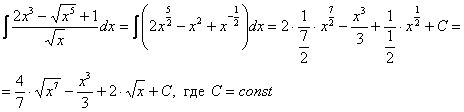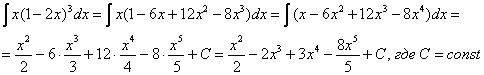интеграл с чего начать

Интегралы для чайников: как решать, правила вычисления, объяснение

Решение интегралов – задача легкая, но только для избранных. Эта статья для тех, кто хочет научиться понимать интегралы, но не знает о них ничего или почти ничего. Интеграл. Зачем он нужен? Как его вычислять? Что такое определенный и неопределенный интегралы?

Если единственное известное вам применение интеграла – доставать крючком в форме значка интеграла что-то полезное из труднодоступных мест, тогда добро пожаловать! Узнайте, как решать простейшие и другие интегралы и почему без этого никак нельзя обойтись в математике.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Изучаем понятие « интеграл »

Интегрирование было известно еще в Древнем Египте. Конечно, не в современном виде, но все же. С тех пор математики написали очень много книг по этой теме. Особенно отличились Ньютон и Лейбниц, но суть вещей не изменилась.

Как понять интегралы с нуля? Никак! Для понимания этой темы все равно понадобятся базовые знания основ математического анализа. Сведения о пределах и производных, необходимые и для понимания интегралов, уже есть у нас в блоге.

Неопределенный интеграл

Пусть у нас есть какая-то функция f(x).

Неопределенным интегралом функции f(x) называется такая функция F(x), производная которой равна функции f(x).

Другими словами интеграл – это производная наоборот или первообразная. Кстати, о том, как вычислять производные, читайте в нашей статье.

Первообразная существует для всех непрерывных функций. Также к первообразной часто прибавляют знак константы, так как производные функций, различающихся на константу, совпадают. Процесс нахождения интеграла называется интегрированием.

Простой пример:

Чтобы постоянно не высчитывать первообразные элементарных функций, их удобно свести в таблицу и пользоваться уже готовыми значениями.

Полная таблица интегралов для студентов

Определенный интеграл

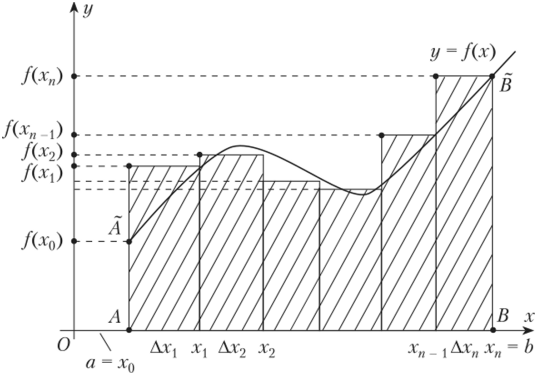
Имея дело с понятием интеграла, мы имеем дело с бесконечно малыми величинами. Интеграл поможет вычислить площадь фигуры, массу неоднородного тела, пройденный при неравномерном движении путь и многое другое. Следует помнить, что интеграл – это сумма бесконечно большого количества бесконечно малых слагаемых.

В качестве примера представим себе график какой-нибудь функции.

Как найти площадь фигуры, ограниченной графиком функции? С помощью интеграла! Разобьем криволинейную трапецию, ограниченную осями координат и графиком функции, на бесконечно малые отрезки. Таким образом фигура окажется разделена на тонкие столбики. Сумма площадей столбиков и будет составлять площадь трапеции. Но помните, что такое вычисление даст примерный результат. Однако чем меньше и уже будут отрезки, тем точнее будет вычисление. Если мы уменьшим их до такой степени, что длина будет стремиться к нулю, то сумма площадей отрезков будет стремиться к площади фигуры. Это и есть определенный интеграл, который записывается так:

Точки а и b называются пределами интегрирования.

Бари Алибасов и группа

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Правила вычисления интегралов для чайников

Свойства неопределенного интеграла

Как решить неопределенный интеграл? Здесь мы рассмотрим свойства неопределенного интеграла, которые пригодятся при решении примеров.

Свойства определенного интеграла

Как считать определенный интеграл? С помощью формулы Ньютона-Лейбница.

Мы уже выяснили, что определенный интеграл – это предел суммы. Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:

Примеры решения интегралов

Ниже рассмотрим неопределенный интеграл и примеры с решением. Предлагаем самостоятельно разобраться в тонкостях решения, а если что-то непонятно, задавайте вопросы в комментариях.

Для закрепления материала посмотрите видео о том, как решаются интегралы на практике. Не отчаиваетесь, если интеграл не дается сразу. Обратитесь в профессиональный сервис для студентов, и любой тройной или криволинейный интеграл по замкнутой поверхности станет вам по силам.

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник

Интегралы – что это, как решать, примеры решений и объяснение для чайников

За 4 минуты вы узнаете, что такое интегрирование. Как интеграл связан с производными. Чем отличается определенный интеграл от неопределенного. 5 примеров вычисления интегралов

Почему вы не знаете, как решать интегралы

А для чего нужны интегралы? Попробуйте сами себе ответить на этот вопрос.

Объясняя тему интегралов, учителя перечисляют малополезные школьным умам области применения. Среди них:

Связать все эти процессы не всегда получается, поэтому многие ученики путаются, даже при наличии всех базовых знаний для понимания интеграла.

Главная причина незнания – отсутствие понимания практической значимости интегралов.

Нужна помощь в написании работы?

Написание учебной работы за 1 день от 100 рублей. Посмотрите отзывы наших клиентов и узнайте стоимость вашей работы.

Интеграл – что это?

Предпосылки. Потребность в интегрировании возникла в Древней Греции. В то время Архимед начал применять для нахождения площади окружности методы, похожие по сути на современные интегральные исчисления. Основным подходом для определения площади неровных фигур тогда был «Метод исчерпывания», который достаточно лёгок для понимания.

Суть метода. В данную фигуру вписывается монотонная последовательность других фигур, а затем вычисляется предел последовательности их площадей. Этот предел и принимался за площадь данной фигуры.

Метод исчерпывания для определения площади круга

В этом методе легко прослеживается идея интегрального исчисления, которая заключается в нахождении предела бесконечной суммы. В дальнейшем эта идея применялась учёными для решения прикладных задач астронавтики, экономики, механики и др.

Современный интеграл. Классическая теория интегрирования была сформулирована в общем виде Ньютоном и Лейбницем. Она опиралась на существовавшие тогда законы дифференциального исчисления. Для её понимания, необходимо иметь некоторые базовые знания, которые помогут математическим языком описать визуальные и интуитивные представления об интегралах.

Объясняем понятие «Интеграл»

Процесс нахождения производной называется дифференцированием, а нахождение первообразной – интегрированием.

Интеграл математическим языком – это первообразная функции (то, что было до производной) + константа «C».

Интеграл простыми словами – это площадь криволинейной фигуры. Неопределенный интеграл – вся площадь. Определенный интеграл – площадь в заданном участке.

Интеграл записывается так:

Каждая подынтегральная функция умножается на компонент «dx». Он показывает, по какой переменной осуществляется интегрирование. «dx» – это приращение аргумента. Вместо X может быть любой другой аргумент, например t (время).

Неопределённый интеграл

Неопределенный интеграл не имеет границ интегрирования.

Для решения неопределённых интегралов достаточно найти первообразную подынтегральной функции и прибавить к ней «C».

Определённый интеграл

В определенном интеграле на знаке интегрирования пишут ограничения «a» и «b». Они указаны на оси X в графике ниже.

Точки A и B на оси X – есть ограничение зоны определения интеграла

Для вычисления определенного интеграла необходимо найти первообразную, подставить в неё значения «a» и «b» и найти разность. В математике это называется формулой Ньютона-Лейбница:

Таблица интегралов для студентов (основные формулы)

Скачайте формулы интегралов, они вам еще пригодятся

Как вычислять интеграл правильно

Существует несколько простейших операций для преобразования интегралов. Вот основные из них:

Вынесение константы из-под знака интеграла

Разложение интеграла суммы на сумму интегралов

Если поменять местами a и b, знак изменится

Можно разбить интеграл на промежутки следующим образом

Это простейшие свойства, на основе которых потом будут формулироваться более сложные теоремы и методы исчисления.

Примеры вычисления интегралов

Решение неопределенного интеграла

Решение определенного интеграла

Базовые понятия для понимания темы

Чтобы вы поняли суть интегрирования и не закрыли страницу от непонимания, мы объясним ряд базовых понятий. Что такое функция, производная, предел и первообразная.

Функция – правило, по которому все элементы из одного множества соотносятся со всеми элементами из другого.

Производная – функция, описывающая скорость изменения другой функции в каждой конкретной точке. Если говорить строгим языком, – это предел отношения приращения функции к приращению аргумента. Он вычисляется вручную, но проще использовать таблицу производных, в которой собрано большинство стандартных функций.

Приращение – количественное изменение функции при некотором изменении аргумента.

Предел – величина, к которой стремиться значение функции, при стремлении аргумента к определённому значению.

Пример предела: допустим при X равном 1, Y будет равно 2. Но что, если X не равен 1, а стремится к 1, то есть никогда её не достигает? В этом случае y никогда не достигнет 2, а будет только стремиться к этой величине. На математическом языке это записывается так: limY(X), при X –> 1 = 2. Читается: предел функции Y(X), при x стремящемся к 1, равен 2.

Как уже было сказано, производная – это функция, описывающая другую функцию. Изначальная функция может быть производной для какой-либо другой функции. Эта другая функция называется первообразной.

Заключение

Найти интегралы не трудно. Если вы не поняли, как это делать, прочитайте статью еще раз. Со второго раза становится понятнее. Запомните! Решение интегралов сводится к простым преобразованиям подынтегральной функции и поиска её в таблице интегралов.

Если текстовое объяснение вам не заходит, посмотрите видео о смысле интеграла и производной:

Источник

Неопределенный интеграл.
Подробные примеры решений

На данном уроке мы начнём изучение темы Неопределенный интеграл, а также подробно разберем примеры решений простейших (и не совсем) интегралов. В этой статье я ограничусь минимумом теории, и сейчас наша задача – научиться решать интегралы.

Что нужно знать для успешного освоения материала? Для того чтобы справиться с интегральным исчислением Вам необходимо уметь находить производные, минимум, на среднем уровне. Поэтому, если материал запущен, то рекомендую сначала внимательно ознакомиться с уроками Как найти производную? и Производная сложной функции. Не лишним опытом будет, если у Вас за плечами несколько десятков (лучше – сотня) самостоятельно найденных производных. По-крайне мере, Вас не должны ставить в тупик задания на дифференцирование простейших и наиболее распространенных функций. Казалось бы, при чем здесь вообще производные, если речь в статье пойдет об интегралах?! А дело вот в чем. Дело в том, что нахождение производных и нахождение неопределенных интегралов (дифференцирование и интегрирование) – это два взаимно обратных действия, как, например, сложение/вычитание или умножение/деление. Таким образом, без навыка (+ какого-никакого опыта) нахождения производных, к сожалению, дальше не продвинуться.

В этой связи нам потребуются следующие методические материалы: Таблица производных и Таблица интегралов. Справочные пособия можно открыть, закачать или распечатать на странице Математические формулы и таблицы.

В чем сложность изучения неопределенных интегралов? Если в производных имеют место строго 5 правил дифференцирования, таблица производных и довольно четкий алгоритм действий, то в интегралах всё иначе. Существуют десятки способов и приемов интегрирования. И, если способ интегрирования изначально подобран неверно (т.е. Вы не знаете, как решать), то интеграл можно «колоть» буквально сутками, как самый настоящий ребус, пытаясь приметить различные приемы и ухищрения. Некоторым даже нравится. Между прочим, это не шутка, мне довольно часто приходилось слышать от студентов мнение вроде «У меня никогда не было интереса решить предел или производную, но вот интегралы – совсем другое дело, это увлекательно, всегда есть желание «взломать» сложный интеграл». Стоп. Хватит чёрного юмора, переходим к этим самым неопределенным интегралам.

Коль скоро способов решения существует очень много, то с чего же начать изучение неопределенных интегралов чайнику? В интегральном исчислении существуют, на мой взгляд, три столпа или своеобразная «ось», вокруг которой вращается всё остальное. В первую очередь следует хорошо разобраться в простейших интегралах (эта статья). Потом нужно детально проработать урок Метод замены в неопределенном интеграле. ЭТО ВАЖНЕЙШИЙ ПРИЁМ! Может быть, даже самая важная статья из всех моих статей, посвященных интегралам. И, в-третьих, обязательно следует ознакомиться с методом интегрирования по частям, поскольку с помощью него интегрируется обширный класс функций. Если Вы освоите хотя бы эти три урока, то уже «не два». Вам могут «простить» незнание интегралов от тригонометрических функций, интегралов от дробей, интегралов от дробно-рациональных функций, интегралов от иррациональных функций (корней), но вот если «сесть в лужу» на методе замены или методе интегрирования по частям – то это будет очень и очень скверно.

В Рунете сейчас весьма распространены демотиваторы. В контексте изучения интегралов, наоборот, просто необходим МОТИВАТОР. Как в том анекдоте про Василия Ивановича, который и Петьку мотивировал, и Аньку мотивировал. Уважаемые лентяи, халявщики и другие нормальные студенты, обязательно прочитайте нижеследующее. Знания и навыки по неопределенному интегралу потребуются в дальнейшей учебе, в частности, при изучении определенного интеграла, несобственных интегралов, дифференциальных уравнений на 2 курсе. Необходимость взять интеграл возникает даже в теории вероятностей! Таким образом, без интегралов путь на летнюю сессию и 2 курс БУДЕТ РЕАЛЬНО ЗАКРЫТ. Я серьезно. Вывод таков. Чем больше интегралов различных типов вы прорешаете, тем легче будет дальнейшая жизнь. Да, это займет довольно много времени, да, порой, не хочется, да, иногда «да фиг с ним, с этим интегралом, авось не попадется». Но, воодушевлять и греть душу должна следующая мысль, ваши усилия окупятся сполна! Вы будете, как орехи щелкать дифференциальные уравнения и легко расправляться с интегралами, которые встретятся в других разделах высшей математики. Качественно разобравшись с неопределенным интегралом, ВЫ ФАКТИЧЕСКИ ОСВАИВАЕТЕ ЕЩЕ НЕСКОЛЬКО РАЗДЕЛОВ ВЫШКИ.

И поэтому я просто не мог не создать интенсивный курс по технике интегрирования, который получился на удивление коротким – желающие могут воспользоваться pdf-книгой и подготовиться ОЧЕНЬ быстро. Но материалы сайта ни в коем случае не хуже!

Итак, начинаем с простого. Посмотрим на таблицу интегралов. Как и в производных, мы замечаем несколько правил интегрирования и таблицу интегралов от некоторых элементарных функций. Нетрудно заметить, что любой табличный интеграл (да и вообще любой неопределенный интеграл) имеет вид:

Сразу разбираемся в обозначениях и терминах:

– значок интеграла.

– подынтегральная функция (пишется с буквой «ы»).

– значок дифференциала. При записи интеграла и в ходе решения важно не терять данный значок. Заметный недочет будет.

– подынтегральное выражение или «начинка» интеграла.

– первообразная функция.

– множество первообразных функций. Не нужно сильно загружаться терминами, самое важное, что в любом неопределенном интеграле к ответу приплюсовывается константа .

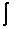
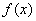
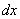
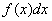
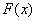
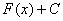
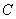
Решить интеграл – это значит найти определенную функцию 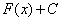, пользуясь некоторыми правилами, приемами и таблицей.

Еще раз посмотрим на запись:

Посмотрим в таблицу интегралов.

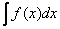
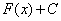
Что происходит? Левые части у нас превращаются в другие функции: .

Упростим наше определение.

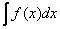
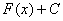
Решить неопределенный интеграл – это значит ПРЕВРАТИТЬ его в определенную функцию , пользуясь некоторыми правилами, приемами и таблицей.

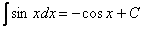
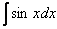
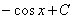
Возьмем, например, табличный интеграл . Что произошло? превратился в функцию .

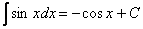
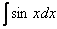
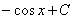
Как и в случае с производными, для того, чтобы научиться находить интегралы, не обязательно быть в курсе, что такое интеграл, первообразная функция с теоретической точки зрения. Достаточно просто осуществлять превращения по некоторым формальным правилам. Так, в случае совсем не обязательно понимать, почему интеграл превращается именно в . Пока можно принять эту и другие формулы как данность. Все пользуются электричеством, но мало кто задумывается, как там по проводам бегают электроны.

Так как дифференцирование и интегрирование – противоположные операции, то для любой первообразной, которая найдена правильно, справедливо следующее:

Иными словами, если продифференцировать правильный ответ, то обязательно должна получиться исходная подынтегральная функция.

Вернемся к тому же табличному интегралу .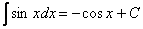

Убедимся в справедливости данной формулы. Берем производную от правой части:

– исходная подынтегральная функция.

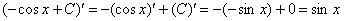
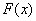
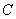
Вот, кстати, стало понятнее, почему к функции всегда приписывается константа . При дифференцировании константа всегда превращается в ноль.

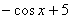
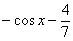
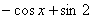
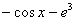
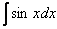
Решить неопределенный интеграл – это значит найти множество всех первообразных, а не какую-то одну функцию. В рассматриваемом табличном примере , , , и т. д. – все эти функции являются решением интеграла . Решений бесконечно много, поэтому записывают коротко:

Таким образом, любой неопределенный интеграл достаточно легко проверить (в отличие от производных, где хорошую стопудовую проверку можно осуществить разве что с помощью математических программ). Это некоторая компенсация за большое количество интегралов разных видов.

Переходим к рассмотрению конкретных примеров. Начнем, как и при изучении производной,
с двух правил интегрирования, которые также называют свойствами линейности неопределенного интеграла:

– постоянный множитель можно (и нужно) вынести за знак интеграла.

– интеграл от алгебраической суммы двух функций равен алгебраической сумме двух интегралов от каждой функции в отдельности. Данное свойство справедливо для любого количества слагаемых.

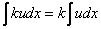
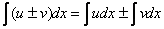
Как видите, правила, в принципе, такие же, как и для производных.

Найти неопределенный интеграл. Выполнить проверку.

Решение: Удобнее переписать его на бумагу.

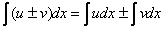
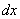
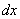
(1) Применяем правило . Не забываем записать значок дифференциала под каждым интегралом. Почему под каждым? – это полноценный множитель, если расписывать решение совсем детально, то первый шаг следует записать так:

(2) Согласно правилу 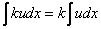, выносим все константы за знаки интегралов. Обратите внимание, что в последнем слагаемом – это константа, её также выносим.
Кроме того, на данном шаге готовим корни и степени для интегрирования. Точно так же, как и при дифференцировании, корни надо представить в виде 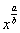. Корни и степени, которые располагаются в знаменателе – перенести вверх.

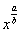
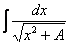
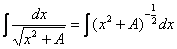
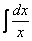
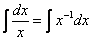
! Примечание: в отличие от производных, корни в интегралах далеко не всегда следует приводить к виду , а степени переносить вверх. Например, – это готовый табличный интеграл, и всякие китайские хитрости вроде совершенно не нужны. Аналогично: – тоже табличный интеграл, нет никакого смысла представлять дробь в виде . Внимательно изучите таблицу!

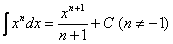
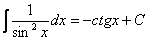
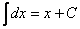
(3) Все интегралы у нас табличные. Осуществляем превращение с помощью таблицы, используя формулы: , и .
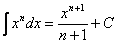
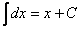
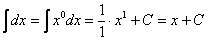
Особое внимание обращаю на формулу интегрирования степенной функции , она встречается очень часто, ее лучше запомнить. Следует отметить, что табличный интеграл – частный случай этой же формулы: .
Константу 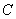достаточно приплюсовать один раз в конце выражения (а не ставить их после каждого интеграла).
(4) Записываем полученный результат в более компактном виде, все степени вида 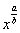снова представляем в виде корней, степени с отрицательным показателем – сбрасываем обратно в знаменатель.

Проверка. Для того чтобы выполнить проверку нужно продифференцировать полученный ответ:

Получена исходная подынтегральная функция, значит, интеграл найден правильно. От чего плясали, к тому и вернулись. Знаете, очень хорошо, когда история с интегралом заканчивается именно так.

Время от времени встречается немного другой подход к проверке неопределенного интеграла, от ответа берется не производная, а дифференциал: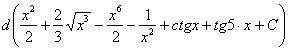

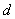
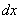
Кто с первого семестра понял, тот понял, но сейчас нам важны не теоретические тонкости, а важно то, что с этим дифференциалом дальше делать. Его необходимо раскрыть, и с формально-технической точки зрения – это почти то же самое, что найти производную. Дифференциал раскрывается следующим образом: значок убираем, справа над скобкой ставим штрих, в конце выражения приписываем множитель :

Получено исходное подынтегральное выражение, значит, интеграл найден правильно.

Второй способ проверки мне нравится меньше, так как приходится дополнительно рисовать большие скобки и тащить значок дифференциала 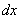до конца проверки. Хотя он корректнее или «солиднее» что ли.

На самом деле я вообще мог умолчать о втором способе проверки. Дело не в способе, а в том, что мы научились раскрывать дифференциал. Еще раз.

Дифференциал раскрывается следующим образом:

1) значок 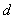убираем;
2) справа над скобкой ставим штрих (обозначение производной);
3) в конце выражения приписываем множитель .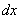

Например:

Запомните это. Рассмотренный приём потребуется нам очень скоро.

Найти неопределенный интеграл. Выполнить проверку.

Это пример для самостоятельно решения. Ответ и полное решение в конце урока.

Когда мы находим неопределенный интеграл, то ВСЕГДА стараемся сделать проверку, тем более, для этого есть прекрасная возможность. Далеко не все типы задач в высшей математике является подарком с этой точки зрения. Неважно, что часто в контрольных заданиях проверки не требуется, её никто, и ничто не мешает провести на черновике. Исключение можно сделать лишь тогда, когда не хватает времени (например, на зачете, экзамене). Лично я всегда проверяю интегралы, а отсутствие проверки считаю халтурой и некачественно выполненным заданием.

Найти неопределенный интеграл. Выполнить проверку.

Решение: Анализируя интеграл, мы видим, что у нас произведение двух функций, да еще и возведение в степень целого выражения. К сожалению, на поприще интегральной битвы нет хороших и удобных формул для интегрирования произведения и частного , .

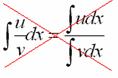
А поэтому, когда дано произведение или частное, всегда имеет смысл посмотреть, а нельзя ли преобразовать подынтегральную функцию в сумму?

Рассматриваемый пример – тот случай, когда можно. Сначала я приведу полное решение, комментарии будут ниже.

(1) Используем старую-добрую формулу квадрата суммы 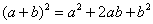, избавляясь от степени.

(2) Вносим в скобку, избавляясь от произведения.

(4) Превращаем интегралы по табличной формуле .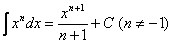

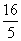
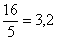
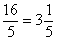
(5) Упрощаем ответ. Здесь следует обратить внимание на обыкновенную неправильную дробь – она несократима и в ответ входит именно в таком виде. Не нужно делить на калькуляторе ! Не нужно представлять ее в виде !

Проверка:

Получена исходная подынтегральная функция, значит, интеграл найден правильно.

В ходе проверки функцию всегда желательно «упаковать» до первоначального вида, вынося в данном случае 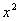за скобки и применяя формулу сокращенного умножения в обратном направлении:

Найти неопределенный интеграл. Выполнить проверку.

Это пример для самостоятельно решения. Ответ и полное решение в конце урока.

Найти неопределенный интеграл. Выполнить проверку.

В данном примере подынтегральная функция представляет собой дробь. Когда мы видим в подынтегральном выражении дробь, то первой мыслью должен быть вопрос: А нельзя ли как-нибудь от этой дроби избавиться, или хотя бы её упростить?

Замечаем, что в знаменателе находится одинокий корень из «икс». Один в поле – не воин, а значит, можно почленно разделить числитель на знаменатель:

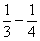
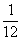
Действия с дробными степенями я не комментирую, так как о них неоднократно шла речь в статьях о производной функции. Если Вас все-таки ставит в тупик такой пример, как , и ни в какую не получается правильный ответ , то рекомендую обратиться к школьным учебникам. В высшей математике дроби и действия с ними встречаются на каждом шагу.

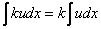
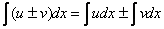
Также обратите внимание, что в решении пропущен один шаг, а именно, применение правил , . Обычно уже при начальном опыте решения интегралов данные свойства считают само собой разумеющимися и не расписывают подробно.

Найти неопределенный интеграл. Выполнить проверку.

Это пример для самостоятельно решения. Ответ и полное решение в конце урока.

В общем случае с дробями в интегралах не всё так просто, дополнительный материал по интегрированию дробей некоторых видов можно найти в статье Интегрирование некоторых дробей.

! Но, прежде чем перейти к вышеуказанной статье, необходимо ознакомиться с уроком Метод замены в неопределенном интеграле. Дело в том, что подведение функции под дифференциал или метод замены переменной является ключевым моментом в изучении темы, поскольку встречается не только «в чистых заданиях на метод замены», но и во многих других разновидностях интегралов.

Очень хотелось включить еще несколько примеров в данный урок, но вот сижу сейчас, печатаю этот текст в Вёрде и замечаю, что статья уже выросла до приличных размеров.
А поэтому вводный курс интегралов для чайников подошел к концу.

Пример 2: Решение:

Пример 4: Решение:

В данном примере мы использовали формулу сокращенного умножения

Пример 6: Решение:

Я выполнил проверку, а Вы? 😉

Автор: Емелин Александр

(Переход на главную страницу)

Zaochnik.com – профессиональная помощь студентам

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

Tutoronline.ru – онлайн репетиторы по математике и другим предметам

Источник