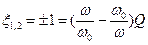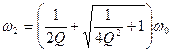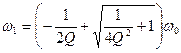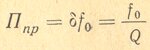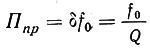к чему будет стремиться ширина полосы пропускания идеального контура

Избирательные свойства последовательного колебательного контура. Добротность, резонансная частота, полоса пропускания, связь между ними

Способность электрической цепи выделять колебания отдельных частот из суммы колебаний различных частот называется избирательностью.

В идеальном случае отклик избирательной цепи должен иметь постоянное значение в пределах определенного диапазона частот, называемого полосой пропускания цепи, и быть равным нулю за пределами этого диапазона.

Рис. 6.15. Нормированные АЧХ избирательной цепи: 1 — идеальной; 2 — реальной.

Ширина полосы пропускания пропорциональна резонансной частоте контура 2∆ω = ω_в – ω_н = ω₀/Q. Таким образом, избирательные свойства последовательного колебательного контура зависят от его добротности: чем выше добротность контура, тем меньше ширина полосы пропускания.

Параллельный колебательный контур. Разновидности параллельных колебательных контуров. Комплексная проводимость, комплексное сопротивление параллельного контура с параллельным включением

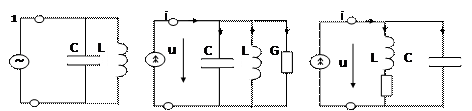
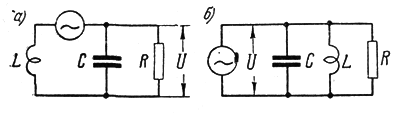
Параллельным колебательным контуром называется электрическая цепь, в которой индуктивные катушки и конденсаторы размещены в двух ветвях, подключенных параллельно источнику энергии. Принципиальная электрическая схема параллельного контура, а также его различные эквивалентные схемы приведены на рис. 6.17.

В соответствии с основным методом теории цепей реальные элементы заменим упрощенными моделирующими цепями, а принципиальную электрическую схему контура его эквивалентной схемой. Используя параллельные схемы замещения источника энергии, индуктивной катушки и конденсатора, получим один из вариантов эквивалентной схемы контура (рис. 6.17, б). Пусть элементы контура имеют высокую добротность, при этом зависимостью L_nap от частоты можно пренебречь и считать, что параметры реактивных элементов параллельной и последовательной схем замещения индуктивной катушки и конденсатора одинаковы: L_пар = L_посл = L ;С_пар = С_посл = С(6.56)

Проводимость G представляет собой суммарную проводимость потерь индуктивной катушки и конденсатора:G= 1/R_Cпар+1/R_Lпар (6.57)

Рис. 6.17. Схемы параллельных колебательных контуров: а – принципиальная,; б — основного вида; в — с использованием последовательной схемы замещения индуктивной катушки. Если каждый из пассивных элементов контура заменить последовательной схемой замещения и пренебречь потерями в конденсаторе по сравнению с потерями в индуктивной катушке, то получим эквивалентную схему контура рис. 6.17, в. Комплексное входное сопротивление параллельного колебательного контура, в соответствии с рис. 6.17, равно: 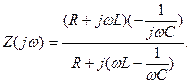(6.72)

Ограничимся, случаем, когда частота внешнего воздействия близка к резонансной и элементы контура имеют высокую добротность (w_pL >> R). Тогда выражение (6.72) можно преобразовать:

(6.73)

Комплексная входная проводимость контура относительно зажимов 1 – 1’ равна Y(jw) = (1/R) + j[wC— 1/(wL)

Комплексные частотные характеристики последовательного колебательного контура, особенности амплитудно-частотной и фазо-частотной характеристики. Резонансная частота, добротность, полоса пропускания, связь между ними.

Частотные характеристики контура будем рассматривать в режиме холостого хода (для параллельного аналогично последовательному) (рис.6.9):

-комплексная входная проводимость: ; (6.29)

-комплексный коэффициент передачи по напряжению для случая, когда напряжение снимается с емкости:

; (6.30)

-комплексный коэффициент передачи по напряжению для случая, когда напряжение снимается с индуктивности:

(6.31)

Комплексный ток контура определяется произведением комплексной входной проводимости контура на комплексное действующее значение э.д.с.. При постоянных действующем значении входного напряжения и нулевой начальной фазе зависимость нормированного входного тока контура от частоты совпадает с нормированной амплитудно-частотной характеристикой входной проводимости контура, а зависимость начальной фазы от частоты совпадает с нормированной фазо-частотной характеристикой контура.

Рис 6.13. Нормированные АЧХ и ФЧХ комплексной проводимости последовательного колебательного контура.

(6.37)

(6.38)

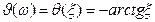
На резонансной частоте

-входное сопротивление контура имеет чисто резистивный характер и равно сопротивлению потерь контура: Z(ω₀) = R;

-действующее значение тока контура I = U/R;

где U — действующее значение напряжения на контуре;

-полное сопротивление емкости равно полному сопротивлению индуктивности:

-действующие значения напряжений на реактивных элементах контура U_C(ω₀) = U_L(ω₀) =ωI. (6.19)

Отношение действующего значения напряжения на реактивном элементе контура к действующему значению напряжения на контуре на резонансной частоте называется добротностью контура

(6.20)

Используя выражение (6.18), добротность колебательного контура Q можно выразить через параметры его элементов:

— связь резонансной частоты и добротности

Как правило, добротность колебательных контуров современной радиотехнической аппаратуры лежит в пределах от нескольких десятков до нескольких сотен, поэтому в режиме резонанса напряжение на реактивных элементах контура может во много раз превышать приложенное к контуру напряжение. При неизменной резонансной частоте ω₀ добротность контура растет с увеличением характеристического сопротивления контура и с уменьшением сопротивления потерь.

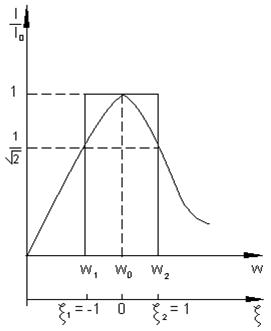
Полоса пропускания реальных избирательных устройств условно определяется как диапазон частот, в пределах которого амплитуда отклика цепи не падает ниже уровня 1/∆ω= 0,707 от максимального значения. На частотах, соответствующих границам полосы пропускания, амплитуда отклика составляет 0,7от максимального значения, а потребляемая цепью активная мощность в 2 раза меньше максимальной.

(6.48)

Ширина полосы пропускания пропорциональна резонансной частоте контура

Таким образом, избирательные свойства последовательного колебательного контура зависят от его добротности: чем выше добротность контура, тем меньше ширина полосы пропускания.

Источник

Полоса пропускания контура управления сервоприводом Комментировать

В конструкции современного сервопривода может быть предусмотрено до трёх типов контуров управления: контур скорости, контур позиционирования и контур тока. Каждый из этих контуров осуществляет контроль одного из перечисленных аспектов, напрямую влияющих на производительность сервомеханизма, и каждому из них присущ общий параметр – полоса пропускания. Этот показатель определяет скорость реагирования устройства на поставленные задачи и возникающие динамические ошибки, а значит, его непременно нужно учитывать при выборе сервопривода.

Чаще всего структура сервопривода подразумевает наличие нескольких контуров управления, вложенных один в другой: контур тока находится в контуре скорости, а контур скорости – в контуре позиционирования. Для эффективной работы такой системы важно, чтобы внутренний контур реагировал на импульс быстрее, чем внешний: для этого внутренние контуры управления оснащаются полосой пропускания, в 5-10 раз превышающие значение этого параметра внешнего контура. Причём данная схема применяется на всех контурах: так, в представленной нами системе контур тока должен иметь большую полосу пропускания, чем контур скорости, а контур скорости, в свою очередь, большую полосу пропускания, чем контур положения.

Широкая полоса пропускания: преимущества и недостатки

Чем шире полоса пропускания, тем лучше динамические характеристики сервомеханизма. Преимуществами широкой полосы пропускания являются:

– увеличение точности позиционирования;
– сокращение времени отклика.

Тем не менее, широкая полоса пропускания имеет и определённые недостатки, ведь чем выше её значение, тем выше частота реагирования двигателя на возмущения.

Факторы, влияющие на максимально допустимую ширину полосы пропускания

При выборе сервомеханизма важно учесть, что значение полосы пропускания прямо пропорционально рассеиванию тепла. Таким образом, увеличение полосы пропускания неминуемо ведёт к повышению нагрева двигателя, а значит, ширина полосы пропускания серводвигателя напрямую зависит от максимально допустимой рабочей температуры электродвигателя. Помимо этого, ограничениями для допустимой ширины полосы пропускания могут стать:

– разрешение устройств обратной связи;
– скорость обновления привода;
– отношение моментов инерции двигателя.

Источник

Полоса пропускания контура

При передачи музыки, речи или телевизионного сигнала требуется определенная полоса частот. Амплитудно-частотная характеристика является сложной функцией расстройки, поэтому для ориентировочных расчетов ее заменяют идеальной характеристикой, имеющей вид прямоугольника с высотой, равной 1 (рис.7.5).

Рисунок 7.5 – Замена АЧХ идеальной АЧХ

Ширина этого прямоугольника по оси часто называется полосой пропускания. Абсолютной полосой пропускания называется величина

(7.29)

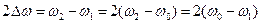
где – нижняя и – верхняя граничные частоты полосы пропускания;

.

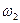
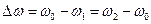
Относительной полосой пропускания называется величина

(7.30)

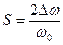
Границы полосы пропускания частот являются величиной условной.

Граничная частота – это та частота, при которой средняя мощность, поглощаемая последовательным контуром, вдвое меньше средней мощности, поглощаемой при резонансе:

,

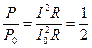
т.е. полагается, что все колебания, мощность которых уменьшается не более, чем в два раза, контуром пропускаются, а все остальные колебания контуром подавляются. При уменьшении мощности в два раза ток должен уменьшаться в 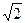раза:

(7.31)

Полоса пропускания последовательного колебательного контура – это диапазон частот, в пределах которого значение АЧХ составляют не менее, чем 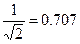ее максимального значения на резонансной частоте (рис. 7.5).

Из выражения (7.31) следует, что на границе полосы пропускания должны выполняться условия:

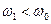
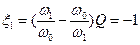
Причем для нижней граничной частоты соответствует уравнение:

(7.32)

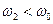
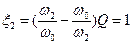
а для верхней граничной частоты соответствует уравнение:

(7.33)

Решая уравнения (7.32) и (7.33) для положительных корней, получим выражение для гармонических частот:

Тогда полоса пропускания равна:

, (7.35)

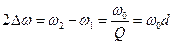
а относительная полоса пропускания равна:

(7.36)

Таким образом, полоса пропускания, характеризующая избирательные свойства колебательного контура, пропорциональна резонансной частоте и обратно пропорциональна добротности; относительная полоса пропускания равна затуханию контура.

Полоса пропускания только приближенно характеризует избирательные свойства контура, но для большинства расчетов точность оказывается вполне достаточной. Для некоторых специальных расчетов, например, для оценки электромагнитной совместимости устройств, учитывают реальные формы АЧХ.

4. Резонанс в параллельном колебательном контуре

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

ПОЛОСА ПРОПУСКАНИЯ КОЛЕБАТЕЛЬНОГО КОНТУРА

Во время передачи тех или иных сигналов ток высокой частоты в антенне радиопередатчика состоит из нескольких токов различной частоты. Такой же сложный характер имеют электромагнитные волны, распространяющиеся от антенны передатчика, и токи, возникающие под действием радиоволн в приемной антенне.

Для каждого вида передачи (радиотелефония, радиотелеграфия, телевизионная передача и т. д.) частоты этих токов занимают определенную полосу. При радиовещании на средних волнах она составляет примерно 9 кГц, т. е. радиовещательный передатчик создает сложный ток, состоящий из нескольких токов, у которых наиболее высокая частота на 9 кГц больше наиболее низкой частоты. Например, для радиовещательного передатчика, работающего на частоте 173 кГц (? =1734 м), это будут частоты от 168,5 до 177,5 кГц. В случае служебной радиотелефонной связи полоса частот не больше 2 — 2,5 кГц, а для радиотелеграфной передачи она еще меньше. Зато при телевизионной передаче полоса частот расширяется до нескольких мегагерц.

При воздействии на контур электродвижущих сил различной частоты наиболее сильные колебания получаются в случае, когда эдс имеет резонансную частоту или частоту, близкую к ней. А при значительном отклонении частоты внешней эдс от резонансного значения, т. е. когда контур расстроен относительно частоты внешней эдс, амплитуда колебаний получается сравнительно малой.

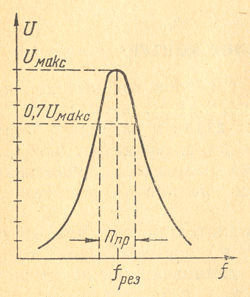
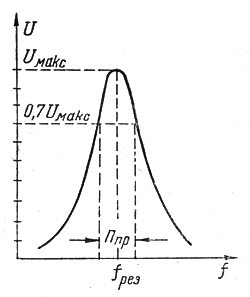
Можно сказать, что каждый контур хорошо пропускает колебания в пределах некоторой полосы частот, располагающейся по обе стороны от резонансной частоты. Ее называют полосой пропускания контура Ппр и условно определяют по резонансной кривой на уровне 0,7 от максимального значения тока или напряжения, соответствующего резонансной частоте (рис.1).

Иначе говоря, считают, что контур хорошо пропускает колебания тогда, когда их амплитуда уменьшается не более, чем на 30% по сравнению с амплитудой при резонансе. Полосу пропускания контура иногда называют также шириной кривой резонанса. Качество контура влияет на форму резонансной кривой. Из этого рисунка видно, что чем ниже качество контура, тем больше его полоса пропускания. Кроме того, полоса пропускания получается больше при более высокой резонансной частоте контура.

Зависимость полосы пропускания контура от его затухания или добротности Q дается следующей простой формулой

Как видно, для получения узкой полосы пропускания необходимо применять контур с высокой добротностью, а для широкой полосы добротность, либо работать на весьма высокой резонансной частоте.

Из приведенной формулы следует, что fo = Q * Ппp. Так как у контура среднего качества Q не менее 20, то рабочая частота должна не менее, чем в 20 раз, превышать полосу пропускания. Например, телевизионную передачу, для которой Ппр составляет несколько мегагерц, нужно вести на частотах не ниже нескольких десятков мегагерц, т.е. на ультракоротких волнах.

Желательно, чтобы контур имел полосу пропускания соответствующую полосе частот, которая характерна для данного вида передачи. Если полоса пропускания меньше, то получатся искажения за счет плохого пропускания некоторых колебаний. Более широкая полоса нежелательна, так как могут быть помехи от сигналов радиостанций, работающих на соседних частотах.

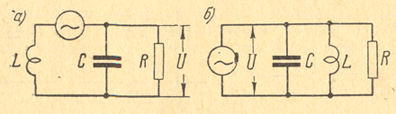
Если необходима широкая полоса пропускания, то приходится часто применять контуры с низкой добротностью. Добротность контура снижается, а полоса пропускания увеличивается, если параллельно контуру присоединяют активное сопротивление R, называемое шунтирующим (рис.2). Действительно, переменное напряжение U, имеющееся на контуре, приложено к сопротивлению R и создает в нем ток. Следовательно, в этом сопротивлении будет расходоваться мощность. Чем меньше сопротивление R, тем больше в нем потери мощности и тем больше затухание контура. Если сопротивление R будет очень малым, то оно замкнет накоротко один из элементов контура (конденсатор на (рис.2 а) или весь контур (рис.2 б). Тогда контур вообще не сможет работать как колебательная система и проявлять свои резонансные свойства.

Шунтирование контура активным сопротивлением делают иногда специально с целью расширения полосы пропускания. Кроме того, подобное шунтирование существует вследствие того, что контур соединен с другими деталями и цепями. За счет этого происходит нежелательное ухудшение качества контура.

Внутреннее сопротивление генератора, питающего параллельный контур, также влияет на добротность контура и его полосу пропускания. Это можно легко объяснить следующим образом.

Пусть генератор в какой-то момент прекратил свое действие. Тогда колебания в контуре станут затухать, а внутреннее сопротивление генератора, присоединенного к контуру, будет играть роль шунтирующего сопротивления, увеличивающего затухание.

Чем больше Ri генератора, тем слабее его влияние, а значит, кривая резонанса контура острее и его полоса пропускания меньше, т.е. резонансные свойства контура выражены резче. При малом Ri генератора добротность контура настолько снижается и полоса пропускания становится такой широкой, что резонансные свойства у контура практически отсутствуют.

К подобному выводу о влиянии Ri генератора мы пришли уже ранее при рассмотрении работы параллельного контура.

Источник

Полоса пропускания контура

Во время передачи тех или иных сигналов ток высокой частоты в антенне радиопередатчика состоит из нескольких токов различной частоты. Такой же сложный характер имеют электромагнитные волны, распространяющиеся от антенны передатчика, и токи, возникающие под действием радиоволн в приемной антенне.

При воздействии на контур электродвижущих сил различной частоты наиболее сильные колебания получаются в случае, когда эде имеет резонансную частоту или частоту, близкую к ней. А при значительном отклонении частоты внешней эде от резонансного значения, т. е. когда контур расстроен относительно частоты внешней эде, амплитуда колебаний получается сравнительно малой.

Можно сказать, что каждый контур хорошо пропускает колебания в пределах некоторой полосы частот, располагающейся по обе стороны от резонансной частоты. Ее называют полосой пропускания контура Ппр и условно определяют по резонансной кривой на уровне 0,7 от максимального значения тока или напряжения, соответствующего резонансной частоте (рис.1).

Иначе говоря, считают, что контур хорошо пропускает колебания тогда, когда их амплитуда уменьшается не более, чем на 30% по сравнению с амплитудой при резонансе. Полосу пропускания контура иногда называют также шириной кривой резонанса. Качество контура влияет на форму резонансной кривой. Из этого рисунка видно, что чем ниже качество контура, тем больше его полоса пропускания. Кроме того, полоса пропускания получается больше при более высокой резонансной частоте контура.

Зависимость полосы пропускания контура от его затухания или добротности Q дается следующей простой формулой

Например, контур, настроенный на частоту fо = 2000 кгц и обладающий затуханием (сигма) = 0,01, имеет полосу пропускания Ппр =0,01 * 2000 = 20 кгц.

Как видно, для получения узкой полосы пропускания необходимо применять контур с высокой добротностью, а для широкой полокую добротность, либо работать на весьма высокой резонансной частоте.

Из приведенной формулы следует, что fo = Q * Ппp. Так как у контура среднего качества Q не менее 20, то рабочая частота должна не менее, чем в 20 раз, превышать полосу пропускания. Например, телевизионную передачу, для которой Ппр составляет несколько мегагерц, нужно вести на частотах не ниже нескольких десятков мегагерц, т.е. на ультракоротких волнах.

Желательно, чтобы контур имел полосу пропускания соответствующую полосе частот, которая характерна для данного вида передачи. Если полоса пропускания меньше, то получатся искажения за счет плохого пропускания некоторых колебаний. Более широкая полоса нежелательна, так как могут быть помехи от сигналов радиостанций, работающих на соседних частотах.

Если необходима широкая полоса пропускания, то приходится часто применять контуры с низкой добротностью. Добротность контура снижается, а полоса пропускания увеличивается, если параллельно контуру присоединяют активное сопротивление R, называемое шунтирующим (рис.2). Действительно, переменное напряжение U, имеющееся на контуре, приложено к сопротивлению R и создает в нем ток. Следовательно, в этом сопротивлении будет расходоваться мощность. Чем меньше сопротивление R, тем больше в нем потери мощности и тем больше затухание контура. Если сопротивление R будет очень малым, то оно замкнет накоротко один из элементов контура (конденсатор на (рис.2 а) или весь контур (рис.2 б). Тогда контур вообще не сможет работать как колебательная система и проявлять свои резонансные свойства.

Шунтирование контура активным сопротивлением делают иногда специально с целью расширения полосы пропускания. Кроме того, подобное шунтирование существует вследствие того, что контур соединен с другими деталями и цепями. За счет этого происходит нежелательное ухудшение качества контура.

Внутреннее сопротивление генератора, питающего параллельный контур, также влияет на добротность контура и его поласу пропускания. Это можно легко объяснить следующим образом.

Пусть генератор в какой-то момент прекратил свое действие. Тогда колебания в контуре станут затухать, а внутреннее сопротивление генератора, присоединенного к контуру, будет играть роль шунтирующего сопротивления, увеличивающего затухание.

Чем больше Ri генератора, тем слабее его влияние, а значит, кривая резонанса контура острее и его полоса пропускания меньше, т.е. резонансные свойства контура выражены резче. При малом Ri генератора добротность контура настолько снижается и полоса пропускания становится такой широкой, что резонансные свойства у контура практически отсутствуют.

К подобному выводу о влиянии Ri генератора мы пришли уже ранее при рассмотрении работы параллельного контура.

Источник