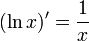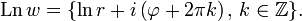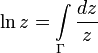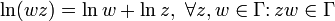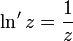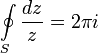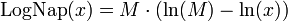Таблица логарифмов что это
Что такое логарифм. Как посчитать логарифм. Свойства логарифмов. Примеры решения логарифмов
Многие школьники считают логарифмы сложной темой в курсе математики. Но если разобрать, что такое логарифм подробно, от простого к сложному, то на ЕГЭ вы не станете их опасаться.
Часто у учеников возникает путаница, где аргумент, а где основание логарифма. И что же нужно возвести в степень, чтобы этот логарифм, наконец, посчитать.
В этой статье мы откроем секрет, как легче запомнить принцип решения логарифма.
Итак, давайте разбираться, что такое логарифм.
Что такое логарифм и как его посчитать
Логарифм имеет следующий вид:

b – это аргумент логарифма
Чтобы узнать значение логарифма приравняем его к X.

Чтобы было легче, можно запоминать так – основание всегда остается внизу (и в первом, и во втором выражении a внизу)!
Чтобы вычислить данный логарифм, необходимо приравнять его к X и воспользоваться правилом, описанным выше:

Логарифмы со специальным обозначением
Для некоторых логарифмов в математике введены специальные обозначения. Это связано с тем, что такие логарифмы встречаются особенно часто. К таким логарифмам относятся десятичный логарифм и натуральный логарифм. Для этих логарифмов справедливы все правила, что и для обычных логарифмов.
Десятичный логарифм
Десятичный логарифм обозначается lg и имеет основание 10, т.е.

Например, вычислим lg100
Натуральный логарифм
Натуральный логарифм обозначается ln и имеет основание e, то есть
Чтобы вычислить данный логарифм нужно число е возвести в степень x. Некоторые из вас спросят, что это за число такое е? Число е – это иррациональное число, т.е. точное его значение вычислить невозможно. е = 2,718281…
Сейчас не будем подробно разбирать, зачем это число нужно, просто запомним, что
И вычислить его можно таким образом:
Основные свойства логарифмов
Логарифмы можно преобразовывать, но для этого необходимо знать правила, которые называются основными свойствами логарифмов. Данные свойства обязательно нужно знать каждому ученику! Без знания этих свойств невозможно решить ни одну серьезную логарифмическую задачу. Вот эти свойства:
Совет – тренируйтесь применять эти свойства в обе стороны, то есть как слева направо, так и справа налево!
Рассмотрим свойства логарифмов на примерах.
Логарифмический ноль и логарифмическая единица
Это следствия из определения логарифма. И их нужно обязательно запомнить. Эти простейшие свойства нередко вводят учеников в ступор.
Запомните, что логарифм от a по основанию а всегда равен единице:
loga a = 1 – это логарифмическая единица.
Если же в аргументе стоит единица, то такой логарифм всегда равен нулю независимо от основания, так как a 0 = 1:
loga 1 = 0 – логарифмический ноль.
Основное логарифмическое тождество
В первой формуле число m становится степенью, которая стоит в аргументе. Данное число может быть любым. Некоторые выражения могут быть решены только с помощью этого тождества.
Вторая формула по сути является просто переформулированным определением логарифма
Разберем применение тождества на примере:
Необходимо найти значение выражения


Сумма логарифмов. Разница логарифмов
Логарифмы с одинаковыми основаниями можно складывать:

Обратите внимание, что формулы суммы и разности логарифмов верны только для логарифмов с одинаковыми основаниями! Если основания разные, то данные свойства применять нельзя!
Вынесение показателя степени из логарифма
Вынесение показателя степени из логарифма:
Переход к новому основанию

Такие формулы чаще всего нужны при решении логарифмических уравнений и неравенств.
Разберем на примере.
Необходимо найти значение такого выражения
Теперь применим переход к новому основанию для второго логарифма:
10 примеров логарифмов с решением
1. Найти значение выражения















10. Найти значение выражения
Надеюсь, теперь вы разобрались, что такое логарифм.
Логарифмические таблицы
Логарифм числа b по основанию a определяется как показатель степени, в которую надо возвести число a, чтобы получить число b. Обозначение: 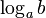
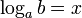
Содержание
Вещественный логарифм
Логарифм вещественного числа logab имеет смысл при 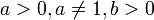
Наиболее широкое применение нашли следующие виды логарифмов.
Свойства
Натуральные логарифмы
Для производной натурального логарифма справедлива простая формула:
По этой причине в математических исследованиях преимущественно используют именно натуральные логарифмы. Они нередко появляются при решении дифференциальных уравнений, исследовании статистических зависимостей (например, распределения простых чисел) и т. п.
При 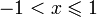
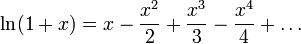 | (1) |
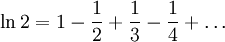 |
Формула (1) не имеет большой практической ценности из-за того, что ряд очень медленно сходится и значение x ограничено весьма узким диапазоном. Однако нетрудно получить из неё более удобную формулу:
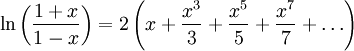 | (2) |
Этот ряд сходится быстрее, а кроме того, левая часть формулы теперь может выразить логарифм любого положительного числа.
Связь с десятичным логарифмом: 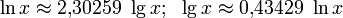
Десятичные логарифмы
Логарифмы по основанию 10 (обозначение: lg a) до изобретения калькуляторов широко применялись для вычислений. Неравномерная шкала десятичных логарифмов обычно наносится и на логарифмические линейки. Подобная шкала широко используется в различных областях науки, например:
Логарифмическая шкала также широко применяется для выявления показателя степени в степенных зависимостях и коэффициента в показателе экспоненты. При этом график, построенный в логарифмическом масштабе по одной или двум осям, принимает вид прямой, более простой для исследования.
Комплексный логарифм
Многозначная функция
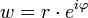
то логарифм 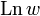
Из формулы следует:
Примеры (приведено главное значение логарифма):
Аналогично рассматриваются комплексные логарифмы с другим основанием. Следует, однако, быть осторожным при преобразованиях комплексных логарифмов, принимая во внимание, что они многозначны, и поэтому из равенства логарифмов каких-либо выражений не следует равенство этих выражений. Пример ошибочного рассуждения:
iπ = ln( − 1) = ln(( − i) 2 ) = 2ln( − i) = 2( − iπ / 2) = − iπ — явная нелепость.
Отметим, что слева стоит главное значение логарифма, а справа — значение из нижележащей ветви ( k = − 1 ). Причина ошибки — неосторожное использования свойства 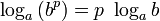
Аналитическое продолжение
При этом, если Γ — простая кривая (без самопересечений), то для чисел, лежащих на ней, логарифмические тождества можно применять без опасений, например
Из формулы аналитического продолжения следует, что на любой ветви логарифма
Интеграл берётся в положительном направлении (против часовой стрелки). Это тождество лежит в основе теории вычетов.
Риманова поверхность
Исторический очерк
Вещественный логарифм
Потребность в сложных расчётах в XVI веке быстро росла, и значительная часть трудностей была связана с умножением и делением многозначных чисел. В конце века нескольким математикам, почти одновременно, пришла в голову идея: заменить трудоёмкое умножение на простое сложение, сопоставив с помощью специальных таблиц геометрическую и арифметическую прогрессии, при этом геометрическая будет исходной. Тогда и деление автоматически заменяется на неизмеримо более простое и надёжное вычитание. Первым эту идею опубликовал в своей книге «Arithmetica integra» Михаэль Штифель, который, впрочем, не приложил серьёзных усилий для реализации своей идеи.
В 1614 году шотландский математик-любитель Джон Непер опубликовал на латинском языке сочинение под названием «Описание удивительной таблицы логарифмов». В нём было краткое описание логарифмов и их свойств, а также 8-значные таблицы логарифмов синусов, косинусов и тангенсов, с шагом 1′. Термин логарифм, предложенный Непером, утвердился в науке.
Строго говоря, Непер табулировал не ту функцию, которая сейчас называется логарифмом. Если обозначить его функцию LogNap(x), то она связана с натуральным логарифмом следующим образом:
Очевидно, LogNap(M) = 0, то есть логарифм «полного синуса» есть нуль — этого и добивался Непер своим определением. LogNap(0) = ∞.
Основное свойство логарифма Непера: если величины образуют геометрическую прогрессию, то их логарифмы образуют прогрессию арифметическую. Однако правила логарифмирования для неперовой функции отличались от правил для современного логарифма.
Например, LogNap(ab) = LogNap(a) + LogNap(b) — LogNap(1).
К сожалению, все значения таблицы Непера содержали вычислительную ошибку после шестого знака. Однако это не помешало новой методике вычислений получить широчайшую популярность, и составлением логарифмических таблиц занялись многие европейские математики, включая Кеплера.
В 1620-е годы Эдмунд Уингейт и Уильям Отред изобрели первую логарифмическую линейку, до появления карманных калькуляторов — незаменимый инструмент инженера.
Близкое к современному понимание логарифмирования — как операции, обратной возведению в степень — впервые появилось у Валлиса и Иоганна Бернулли, а окончательно было узаконено Эйлером в XVIII веке. В книге «Введение в анализ бесконечных» (1748) Эйлер дал современные определения как показательной, так и логарифмической функций, привёл разложение их в степенные ряды, особо отметил роль натурального логарифма.
Эйлеру принадлежит и заслуга распространения логарифмической функции на комплексную область.
Комплексный логарифм
Первые попытки распространить логарифмы на комплексные числа предпринимали на рубеже XVII—XVIII веков Лейбниц и Иоганн Бернулли, однако создать целостную теорию им не удалось — в первую очередь по той причине, что тогда ещё не было ясно определено само понятие логарифма. Дискуссия по этому поводу велась сначала между Лейбницем и Бернулли, а в середине XVIII века — между Даламбером и Эйлером. Бернулли и Даламбер считали, что следует определить log(-x) = log(x). Полная теория логарифмов отрицательных и комплексных чисел была опубликована Эйлером в 1747—1751 годах и по существу ничем не отличается от современной.
Хотя спор продолжался (Даламбер отстаивал свою точку зрения и подробно аргументировал её в статье своей «Энциклопедии» и в других трудах), однако точка зрения Эйлера быстро получила всеобщее признание.
Логарифмические таблицы
Из свойств логарифма следует, что вместо трудоёмкого умножения многозначных чисел достаточно найти (по таблицам) и сложить их логарифмы, а потом по тем же таблицам выполнить потенцирование, то есть найти значение результата по его логарифму. Выполнение деления отличается только тем, что логарифмы вычитаются. Лаплас говорил, что изобретение логарифмов «продлило жизнь астрономов», многократно ускорив процесс вычислений.
Первые таблицы логарифмов опубликовал Джон Непер (1614), и они содержали только логарифмы тригонометрических функций, причём с ошибками. Независимо от него свои таблицы опубликовал Иост Бюрги, друг Кеплера (1620). В 1617 году оксфордский профессор математики Генри Бригс опубликовал таблицы, которые уже включали десятичные логарифмы самих чисел, от 1 до 1000, с 8 (позже — с 14) знаками. Но и в таблицах Бригса обнаружились ошибки. Первое безошибочное издание на основе таблиц Вега (1783) появилось только в 1857 году в Берлине (таблицы Бремивера).
В России первые таблицы логарифмов были изданы в 1703 году при участии Л. Ф. Магницкого. В СССР выпускались несколько сборников таблиц логарифмов.
Таблицы Брадиса (1921) использовались в учебных заведениях и в инженерных расчётах, не требующих большой точности. Они содержали мантиссы десятичных логарифмов чисел и тригонометрических функций, натуральные логарифмы и некоторые другие полезные расчётные инструменты.
Профессиональный сборник для точных вычислений.
Логарифмы: таблица-шпаргалка свойств, формулы, примеры, график
Условия определения логарифма.
Докажем необходимость условия a>0. При a=0 по формулировке логарифма может существовать только при b=0. И соответственно тогда log00 может быть любым отличным от нуля действительным числом, так как нуль в любой отличной от нуля степени есть нуль. Исключить эту неоднозначность дает условие a≠0. А при a рациональных и иррациональных значений логарифма, поскольку степень с рациональным и иррациональным показателем определена лишь для неотрицательных оснований. Именно по этой причине и оговорено условие a>0.
И последнее условие b>0 вытекает из неравенства a>0, поскольку x=logα b, а значение степени с положительным основанием a всегда положительно.
Графики логарифма
Основные методы решения
В результате я часто наблюдаю очень обидные ошибки, когда, например, эти буквы меняются местами. Данную формулу нужно либо понять, либо зубрить, причем второй способ приводит к ошибкам в самые неподходящие и самые ответственные моменты: на экзаменах, контрольных и т. д.
Именно поэтому всем своим ученикам я предлагаю отказаться от стандартной школьной формулы и использовать для решения логарифмических уравнений второй подход, который, как вы уже наверняка догадались из названия, называется канонической формой.
И вот тут мы вспоминаем наше замечательное правило, что любое число b может быть представлено в виде логарифма по основанию а от а в степени b :
Как запомнить эту формулу? Да очень просто. Давайте запишем следующую конструкцию:
b = b · 1 = b · log a a
Разумеется, что при этом возникают все ограничения, которые мы записали вначале. А теперь давайте воспользуемся основным свойством логарифма, и внесем множитель b в качестве степени а. Получим:
b = b · 1 = b · log a a = log a a b
В результате исходное уравнение перепишется в следующем виде:
log a f ( x ) = log a a b → f ( x ) = a b
Вот и все. Новая функция уже не содержит логарифма и решается стандартными алгебраическими приемами.
Конечно, кто-то сейчас возразит: а зачем вообще было придумывать какую-то каноническую формулу, зачем выполнять два дополнительных ненужных шага, если можно было сразу перейти от исходной конструкции к итоговой формуле? Да уже хотя бы затем, что большинство учеников не понимают, откуда берется эта формула и, как следствие, регулярно допускают ошибки при ее применении.
А вот такая последовательность действий, состоящая из трех шагов, позволяет вам решить исходное логарифмическое уравнение, даже если вы не понимаете, откуда берется та самая итоговая формула. Кстати, канонической формулой называется именно эта запись:
log a f ( x ) = log a a b
Удобство канонической формы состоит еще и в том, что ее можно применять для решения очень широкого класса логарифмических уравнений, а не только простейших, которые мы рассматриваем сегодня.
Логарифм как обратная функция к показательной
Особенности логарифмов.
Логарифмы характеризуются отличительными особенностями, которые обусловили их повсеместное употребление для значительного облегчения кропотливых расчетов. При переходе «в мир логарифмов» умножение трансформируется на значительно более легкое сложение, деление — на вычитание, а возведение в степень и извлечение корня трансформируются соответствующе в умножение и деление на показатель степени.
Формулировку логарифмов и таблицу их значений (для тригонометрических функций) впервые издал в 1614 году шотландский математик Джон Непер. Логарифмические таблицы, увеличенные и детализированные прочими учеными, широко использовались при выполнении научных и инженерных вычислений, и оставались актуальными пока не стали применяться электронные калькуляторы и компьютеры.
Что такое логарифм и как его посчитать
Логарифм имеет следующий вид:

b – это аргумент логарифма
Чтобы узнать значение логарифма приравняем его к X. 

Чтобы было легче, можно запоминать так – основание всегда остается внизу (и в первом, и во втором выражении a внизу)!
Чтобы вычислить данный логарифм, необходимо приравнять его к X и воспользоваться правилом, описанным выше:

Примеры решения
А теперь давайте рассмотрим реальные примеры. Итак, решаем:
Давайте перепишем его следующим образом:
Многие ученики торопятся и пытаются сразу возвести число 0,5 в степень, которая пришла к нам из исходной задачи. И действительно, когда вы уже хорошо натренируетесь в решении подобных задач, вы можете сразу выполнять этот шаг.
Однако если сейчас вы только приступаете к изучению этой темы, лучше никуда не торопиться, чтобы не допускать обидных ошибок. Итак, перед нами каноническая форма. Имеем:
Это уже не логарифмическое уравнение, а линейное относительно переменной х. Чтобы решить его, давайте для начала разберемся с числом 0,5 в степени −3. Заметим, что 0,5 — это 1/2.
Все десятичные дроби переводите в обычные, когда вы решаете логарифмическое уравнение.
Переписываем и получаем:
3 x − 1 = 8
3 x = 9
x = 3
Все, мы получили ответ. Первая задача решена.
Вторая задача
Переходим ко второй задаче:
Как видим, это уравнение уже не является простейшим. Уже хотя бы потому, что слева стоит разность, а не один-единственный логарифм по одному основанию.
Следовательно, нужно каким-то образом избавиться от этой разности. В данном случае все очень просто. Давайте внимательно посмотрим на основания: слева стоит число под корнем:
Общая рекомендация: во всех логарифмических уравнениях старайтесь избавиться от радикалов, т. е. от записей с корнями и переходить к степенным функциям, просто потому что показатели этих степеней легко выносятся за знак логарифма и в конечном счета такая запись существенно упрощает и ускоряет вычисления. Вот давайте так и запишем:
Теперь вспоминаем замечательное свойство логарифма: из аргумента, а также из основания можно выносить степени. В случае с основаниями происходит следующее:
log a k b = 1/ k loga b
Другими словами, число, которое стояло в степени основания, выносится вперед и при этом переворачивается, т. е. становится обратным числом. В нашем случае стояла степень основания с показателем 1/2. Следовательно, мы можем вынести ее как 2/1. Получим:
Обратите внимание: ни в коем случае нельзя избавляться от логарифмов на этом шаге. Вспомните математику 4—5 класса и порядок действий: сначала выполняется умножение, а лишь затем — сложение и вычитание. В данном случае мы из 10 элементов вычитаем один такой же:
Теперь наше уравнение выглядит как надо. Это простейшая конструкция, и мы решаем его с помощью канонической формы:
Вот и все. Вторая задача решена.
Третий пример
Переходим к третьей задаче:
lg ( x + 3) = 3 + 2 lg 5
Напомню следующую формулу:
Вот именно этими свойствами мы сейчас и воспользуемся для решения задачи, поскольку она не является простейшей, которую мы записали в самом начале нашего урока.
Для начала заметим, что множитель 2, стоящий перед lg 5, может быть внесен и станет степенью основания 5. Кроме того, свободное слагаемое 3 также представимо в виде логарифма — это очень легко наблюдать из нашей записи.
Судите сами: любое число можно представить в виде log по основанию 10:
3 = log10 10 3 = lg 10 3
Перепишем исходную задачу с учетом полученных изменений:
lg ( x − 3) = lg 1000 + lg 25
lg ( x − 3) = lg 1000 · 25
lg ( x − 3) = lg 25 000
Перед нами снова каноническая форма, причем мы получили ее, минуя стадию преобразований, т. е. простейшее логарифмическое уравнение у нас нигде не всплывало.
Именно об этом я и говорил в самом начале урока. Каноническая форма позволяет решать более широкий класс задач, нежели стандартная школьная формула, которую дают большинство школьных учителей.
Ну и все, избавляемся от знака десятичного логарифма, и получаем простую линейную конструкцию:
x + 3 = 25 000
x = 24 997
Замечание по поводу области определения
Тут бы хотелось привести важное замечание по поводу области определения. Наверняка сейчас найдутся ученики и учителя, которые скажут: «Когда мы решаем выражения с логарифмами, необходимо обязательно помнить, что аргумент f ( x ) должен быть больше нуля!» В связи с этим возникает логичный вопрос: почему ни в одной из рассмотренных задач мы не требовали, чтобы это неравенство выполнялось?
Не переживайте. Никаких лишних корней в этих случаях не возникнет. И это еще одна замечательная хитрость, которая позволяет ускорить решение. Просто знайте, что если в задаче переменная х встречается лишь в одном месте (а точнее — в одном-единственном аргументе одного-единственного логарифма), и больше нигде в нашем случае нет переменной х, то записывать область определения не нужно, потому что она будет выполняться автоматически.
Судите сами: в первом уравнении мы получили, что 3х − 1, т. е. аргумент должен быть равен 8. Это автоматически означает, что 3х − 1 будет больше нуля.
Вот и все, что нужно знать для решения простейших задач. Уже одно это правило вместе с правилами преобразования позволит вам решать очень широкий класс задач.
Но давайте будем честными: для того, чтобы окончательно разобраться с этим приемом, чтобы научиться применять каноническую форму логарифмического уравнения, недостаточно просто посмотреть один видеоурок. Поэтому прямо сейчас скачайте варианты для самостоятельного решения, которые прилагаются к данному видеоуроку и начните решать хотя бы одну из этих двух самостоятельных работ.
Времени у вас уйдет буквально несколько минут. А вот эффект от такого обучения будет намного выше по сравнению с тем, если бы вы просто просмотрели данный видеоурок.
Надеюсь, этот урок поможет разобраться вам с логарифмическими уравнениями. Применяйте каноническую форму, упрощайте выражения с помощью правил работы с логарифмами — и никакие задачи вам будут не страшны. А у меня на сегодня все.
Область определения, множество значений, возрастание, убывание
Логарифм является монотонной функцией, поэтому экстремумов не имеет. Основные свойства логарифма представлены в таблице.
| 1″ sprite”> | ||
| Область определения | 0 | 0 |
| Область значений | – ∞ | – ∞ |
| Монотонность | монотонно возрастает | монотонно убывает |
| Нули, y = 0 | x = 1 | x = 1 |
| Точки пересечения с осью ординат, x = 0 | нет | нет |
| + ∞ | – ∞ | |
| – ∞ | + ∞ |
Когда нужная степень не подбирается
Как я уже говорил, далеко не всегда удается подобрать такую степень. Но это не значит, что такого числа не существует, просто его можно вычислить только на калькуляторе.
Типичные ошибки при решении
Сегодня мы разберем два типичных логарифмических уравнения, на которых спотыкаются многие ученики. На примере этих уравнения мы увидим, какие ошибки чаще всего допускаются в процессе решения и преобразования исходных выражений.
Метод группировки
Сегодня мы разберем два логарифмических уравнения, одно из которых не решается «напролом» и требует специальных преобразований, а второе… впрочем, не буду рассказывать все сразу. Смотрите видео, скачивайте самостоятельную работу — и учитесь решать сложные задачи.Итак, группировка и вынесение общих множителей за скобку. Дополнительно я расскажу вам, какие подводные камни несет область определения логарифмов, и как небольшие замечания по области определений могут существенно менять как корни, так и все решение.
Начнем из группировки. Нам нужно решить следующее логарифмическое уравнение:
log2 x · log2 ( x − 3) + 1 = log2 ( x 2 − 3 x )
В первую очередь отметим, что x 2 − 3 x можно разложить на множители:
Затем вспоминаем замечательную формулу:
Сразу же небольшое замечание: данная формула прекрасно работает, когда а, f и g — обычные числа. Но когда вместо них стоят функции, данные выражения перестают быть равноправными. Представьте себе такую гипотетическую ситуацию:
f g fg будет положительным, следовательно, log a ( fg ) будет существовать, а вот log a f и log a g отдельно существовать не будут, и выполнить такое преобразование мы не сможем.
Игнорирование данного факта приведет к сужению области определения и, как следствие, к потере корней. Поэтому прежде чем выполнять такое преобразование, нужно обязательно заранее убедиться, что функции f и g положительные.
Следовательно, в функции log2 x ( x − 3) каждый множитель будет больше нуля. Поэтому можно смело раскладывать произведение на сумму:
log2 x log2 ( x − 3) + 1 − log2 x − log2 ( x − 3) = 0
На первый взгляд может показаться, что легче не стало. Напротив: количество слагаемых лишь увеличились! Чтобы понять, как действовать дальше, введем новые переменные:
А теперь сгруппируем третье слагаемое с первым:
( a · b − a ) + (1 − b ) = 0
a (1 · b − 1) + (1 − b ) = 0
Заметим, что и в первой, и во второй скобке стоит b − 1 (во втором случае придется вынести «минус» за скобку). Разложим нашу конструкцию на множители:
a (1 · b − 1) − ( b − 1) = 0
А теперь вспоминаем наше замечательно правило: произведение равно нулю, когда хотя бы один из множителей равен нулю:
Вспоминаем, что такое b и а. Получим два простейших логарифмических уравнения, в которых останется лишь избавиться от знаков logи приравнять аргументы:
Мы получили два корня, но это не решение исходного логарифмического уравнения, а лишь кандидаты в ответ. Теперь проверим область определения. Для первого аргумента:
Оба корня удовлетворяют первому требованию. Переходим ко второму аргументу:
А вот здесь уже x = 2 нас не удовлетворяет, зато x = 5 вполне нас устраивает. Следовательно, единственным ответом будет x = 5.
Переходим ко второму логарифмическому равнению. На первый взгляд, оно существенно проще. Однако в процессе его решения мы рассмотрим тонкие моменты, связанные с областью определения, незнание которых существенно усложняет жизнь начинающим ученикам.
log0,7 ( x 2 − 6 x + 2) = log0,7 (7 − 2 x )
Перед нами каноническая форма логарифмического уравнения. Ничего преобразовывать не нужно — даже основания одинаковые. Поэтому просто приравниваем аргументы:
x 2 − 6 x + 2 = 7 − 2 x
x 2 − 6 x + 2 − 7 + 2 x = 0
Перед нами приведенное квадратное уравнение, оно легко решается по формулам Виета:
Но эти корни еще не являются окончательными ответами. Нужно найти область определения, поскольку в исходном уравнении присутствуют два логарифма, т.е. учет области определения строго обязателен.
Итак, выпишем область определения. С одной стороны, аргумент первого логарифма должен быть больше нуля:
Эти требования должны выполняться одновременно. И вот тут начинается самое интересное. Безусловно, мы можем решить каждое из этих неравенств, затем пересечь их и найти область определения всего уравнения. Но зачем так усложнять себе жизнь?
Давайте заметим одну тонкость. Избавляясь от знаков log, мы приравниваем аргументы. Отсюда следует, что требования x 2 − 6 x + 2 > 0 и 7 − 2 x > 0 равносильны. Как следствие, любое из двух неравенств можно вычеркнуть. Давайте вычеркнем самое сложное, а себе оставим обычное линейное неравенство:
x x = −1, потому что x = 5 > 3,5.
Можно записать ответ: x = 1 является единственным решением исходного логарифмического уравнения.
Выводы из данного логарифмического уравнения следующие:
Обратный логарифм
Обратный логарифм (или антилогарифм) числа n – это число, логарифм которого по основанию a равен числу n.
Частные значения
Логарифм по основанию 10 называется десятичным логарифмом и обозначается так:
Логарифм по основанию e называется натуральным логарифмом:
Логарифмы со специальным обозначением
Для некоторых логарифмов в математике введены специальные обозначения. Это связано с тем, что такие логарифмы встречаются особенно часто. К таким логарифмам относятся десятичный логарифм и натуральный логарифм. Для этих логарифмов справедливы все правила, что и для обычных логарифмов.
Десятичный логарифм
Десятичный логарифм обозначается lg и имеет основание 10, т.е.

Например, вычислим lg100
Натуральный логарифм
Натуральный логарифм обозначается ln и имеет основание e, то есть
Чтобы вычислить данный логарифм нужно число е возвести в степень x. Некоторые из вас спросят, что это за число такое е? Число е – это иррациональное число, т.е. точное его значение вычислить невозможно. е = 2,718281…
Сейчас не будем подробно разбирать, зачем это число нужно, просто запомним, что
И вычислить его можно таким образом:
Таблица свойств логарифмов
Ниже представлены основные свойства логарифмов в табличном виде.