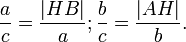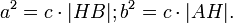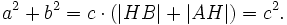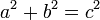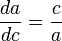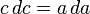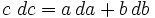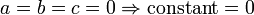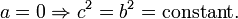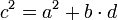Теорема пифагора что это

Пифагора теорема

Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника.

Содержание

Формулировки

Изначально теорема была сформулирована следующим образом:

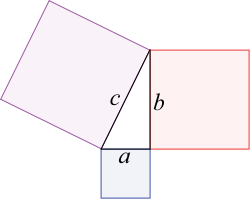
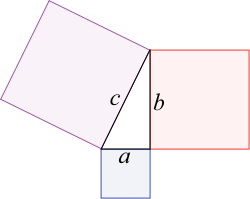
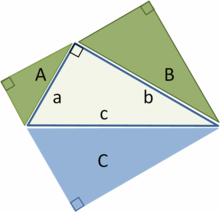
В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.

В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Обе формулировки теоремы эквивалентны, но вторая формулировка более элементарна, она не требует понятия площади. То есть второе утверждение можно проверить, ничего не зная о площади и измерив только длины сторон прямоугольного треугольника.

Обратная теорема Пифагора:

Доказательства

Разумеется, концептуально все их можно разбить на малое число классов. Самые известные из них: доказательства методом площадей, аксиоматические и экзотические доказательства (например с помощью дифференциальных уравнений).

Через подобные треугольники

Следующее доказательство алгебраической формулировки — наиболее простое из доказательств, строящихся напрямую из аксиом. В частности, оно не использует понятие площади фигуры.

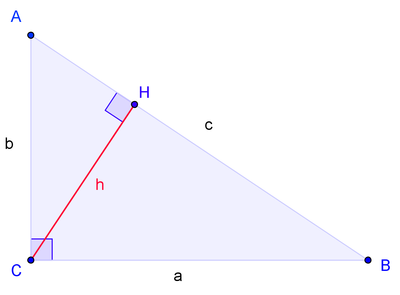
Пусть ABC есть прямоугольный треугольник с прямым углом C. Проведём высоту из C и обозначим её основание через H. Треугольник ACH подобен треугольнику ABC по двум углам. Аналогично, треугольник CBH подобен ABC. Введя обозначения

Доказательства методом площадей

Ниже приведённые доказательства, несмотря на их кажущуюся простоту, вовсе не такие простые. Все они используют свойства площади, доказательства которых сложнее доказательства самой теоремы Пифагора.

Доказательство через равнодополняемость

Что и требовалось доказать.

Доказательства через равносоставленность

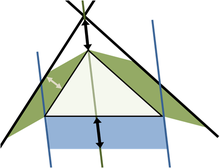
Пример одного из таких доказательств указан на чертеже справа, где квадрат, построенный на гипотенузе, перестановкой преобразуется в два квадрата, построенных на катетах.

Доказательство Евклида

Идея доказательства Евклида состоит в следующем: попробуем доказать, что половина площади квадрата, построенного на гипотенузе, равна сумме половин площадей квадратов, построенных на катетах, а тогда и площади большого и двух малых квадратов равны.

Рассмотрим чертеж слева. На нём мы построили квадраты на сторонах прямоугольного треугольника и провели из вершины прямого угла С луч s перпендикулярно гипотенузе AB, он рассекает квадрат ABIK, построенный на гипотенузе, на два прямоугольника — BHJI и HAKJ соответственно. Оказывается, что площади данных прямоугольников в точности равны площадям квадратов, построенных на соответствующих катетах.

Попытаемся доказать, что площадь квадрата DECA равна площади прямоугольника AHJK Для этого воспользуемся вспомогательным наблюдением: Площадь треугольника с той же высотой и основанием, что и данный прямоугольник, равна половине площади заданного прямоугольника. Это следствие определения площади треугольника как половины произведения основания на высоту. Из этого наблюдения вытекает, что площадь треугольника ACK равна площади треугольника AHK (не изображённого на рисунке), которая, в свою очередь, равна половине площади прямоугольника AHJK.

Докажем теперь, что площадь треугольника ACK также равна половине площади квадрата DECA. Единственное, что необходимо для этого сделать, — это доказать равенство треугольников ACK и BDA (так как площадь треугольника BDA равна половине площади квадрата по указанному выше свойству). Равенство это очевидно, треугольники равны по двум сторонам и углу между ними. Именно — AB=AK,AD=AC — равенство углов CAK и BAD легко доказать методом движения: повернём треугольник CAK на 90° против часовой стрелки, тогда очевидно, что соответствующие стороны двух рассматриваемых треугольников совпадут (ввиду того, что угол при вершине квадрата — 90°).

Рассуждение о равенстве площадей квадрата BCFG и прямоугольника BHJI совершенно аналогично.

Тем самым мы доказали, что площадь квадрата, построенного на гипотенузе, слагается из площадей квадратов, построенных на катетах. Идея данного доказательства дополнительно проиллюстрирована с помощью анимации, расположенной выше.

Доказательство Леонардо да Винчи

Главные элементы доказательства — симметрия и движение.

Доказательство методом бесконечно малых

Следующее доказательство при помощи дифференциальных уравнений часто приписывают известному английскому математику Харди, жившему в первой половине XX века.

Рассматривая чертёж, показанный на рисунке, и наблюдая изменение стороны a, мы можем записать следующее соотношение для бесконечно малых приращений сторон с и a (используя подобие треугольников):

Пользуясь методом разделения переменных, находим

Более общее выражение для изменения гипотенузы в случае приращений обоих катетов

Интегрируя данное уравнение и используя начальные условия, получаем

c 2 = a 2 + b 2 + constant.

Таким образом, мы приходим к желаемому ответу

Как нетрудно видеть, квадратичная зависимость в окончательной формуле появляется благодаря линейной пропорциональности между сторонами треугольника и приращениями, тогда как сумма связана с независимыми вкладами от приращения разных катетов.

Более простое доказательство можно получить, если считать, что один из катетов не испытывает приращения (в данном случае катет b ). Тогда для константы интегрирования получим

Вариации и обобщения

История

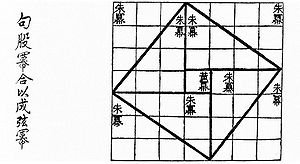
В древнекитайской книге Чу-пей говорится о пифагоровом треугольнике со сторонами 3, 4 и 5: В этой же книге предложен рисунок, который совпадает с одним из чертежей индусской геометрии Басхары.

Кантор (крупнейший немецкий историк математики) считает, что равенство 3 ² + 4 ² = 5² было известно уже египтянам еще около 2300 г. до н. э., во времена царя Аменемхета I (согласно папирусу 6619 Берлинского музея). По мнению Кантора гарпедонапты, или «натягиватели веревок», строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.

Весьма вероятно, что теорема о квадрате гипотенузы была известна в Индии уже около 18 века до н. э.

Источник

Теорема Пифагора

Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника.

Содержание

История

В древнекитайской книге Чу-пей (англ.) (кит. 周髀算經 ) говорится о пифагоровом треугольнике со сторонами 3, 4 и 5. В этой же книге предложен рисунок, который совпадает с одним из чертежей индусской геометрии Басхары.

Мориц Кантор (крупнейший немецкий историк математики) считает, что равенство 3 ² + 4 ² = 5² было известно уже египтянам ещё около 2300 г. до н. э., во времена царя Аменемхета I (согласно папирусу 6619 Берлинского музея). По мнению Кантора, гарпедонапты, или «натягиватели верёвок», строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.

Очень легко можно воспроизвести их способ построения. Возьмём верёвку длиною в 12 м и привяжем к ней по цветной полоске на расстоянии 3 м от одного конца и 4 метра от другого. Прямой угол окажется заключённым между сторонами длиной в 3 и 4 метра. Гарпедонаптам можно было бы возразить, что их способ построения становится излишним, если воспользоваться, например, деревянным угольником, применяемым всеми плотниками. И действительно, известны египетские рисунки, на которых встречается такой инструмент, — например, рисунки, изображающие столярную мастерскую.

Приблизительно в 400 г. до н. э., согласно Проклу, Платон дал метод нахождения пифагоровых троек, сочетающий алгебру и геометрию. Приблизительно в 300 г. до н. э. в «Началах» Евклида появилось старейшее аксиоматическое доказательство теоремы Пифагора. [7]

Формулировки

Изначально теорема была сформулирована следующим образом:

В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.

В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

То есть, обозначив длину гипотенузы треугольника через , а длины катетов через и :

Обе формулировки теоремы эквивалентны, но вторая формулировка более элементарна, она не требует понятия площади. То есть второе утверждение можно проверить, ничего не зная о площади и измерив только длины сторон прямоугольного треугольника.

Обратная теорема Пифагора:

Для всякой тройки положительных чисел , и , такой, что , существует прямоугольный треугольник с катетами и и гипотенузой .

Доказательства

Разумеется, концептуально все их можно разбить на малое число классов. Самые известные из них: доказательства методом площадей, аксиоматические и экзотические доказательства (например, с помощью дифференциальных уравнений).

Через подобные треугольники

Следующее доказательство алгебраической формулировки — наиболее простое из доказательств, строящихся напрямую из аксиом. В частности, оно не использует понятие площади фигуры.

Пусть ABC есть прямоугольный треугольник с прямым углом C. Проведём высоту из C и обозначим её основание через H. Треугольник ACH подобен треугольнику ABC по двум углам. Аналогично, треугольник CBH подобен ABC. Введя обозначения

, что и требовалось доказать

Доказательства методом площадей

Ниже приведённые доказательства, несмотря на их кажущуюся простоту, вовсе не такие простые. Все они используют свойства площади, доказательства которых сложнее доказательства самой теоремы Пифагора.

Доказательство через равнодополняемость

Что и требовалось доказать.

Доказательство Евклида

Идея доказательства Евклида состоит в следующем: попробуем доказать, что половина площади квадрата, построенного на гипотенузе, равна сумме половин площадей квадратов, построенных на катетах, а тогда и площади большого и двух малых квадратов равны.

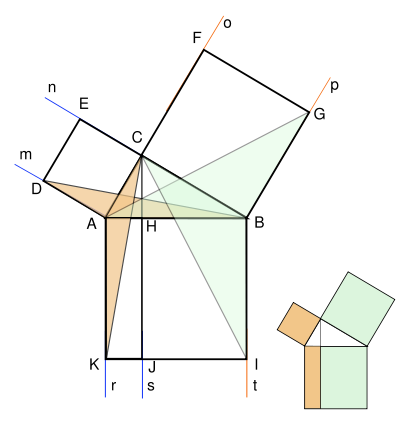
Рассмотрим чертеж слева. На нём мы построили квадраты на сторонах прямоугольного треугольника и провели из вершины прямого угла С луч s перпендикулярно гипотенузе AB, он рассекает квадрат ABIK, построенный на гипотенузе, на два прямоугольника — BHJI и HAKJ соответственно. Оказывается, что площади данных прямоугольников в точности равны площадям квадратов, построенных на соответствующих катетах.

Попытаемся доказать, что площадь квадрата DECA равна площади прямоугольника AHJK Для этого воспользуемся вспомогательным наблюдением: Площадь треугольника с той же высотой и основанием, что и данный прямоугольник, равна половине площади заданного прямоугольника. Это следствие определения площади треугольника как половины произведения основания на высоту. Из этого наблюдения вытекает, что площадь треугольника ACK равна площади треугольника AHK (не изображённого на рисунке), которая, в свою очередь, равна половине площади прямоугольника AHJK.

Докажем теперь, что площадь треугольника ACK также равна половине площади квадрата DECA. Единственное, что необходимо для этого сделать, — это доказать равенство треугольников ACK и BDA (так как площадь треугольника BDA равна половине площади квадрата по указанному выше свойству). Равенство это очевидно: треугольники равны по двум сторонам и углу между ними. Именно — AB=AK, AD=AC — равенство углов CAK и BAD легко доказать методом движения: повернём треугольник CAK на 90° против часовой стрелки, тогда очевидно, что соответствующие стороны двух рассматриваемых треугольников совпадут (ввиду того, что угол при вершине квадрата — 90°).

Рассуждение о равенстве площадей квадрата BCFG и прямоугольника BHJI совершенно аналогично.

Тем самым мы доказали, что площадь квадрата, построенного на гипотенузе, слагается из площадей квадратов, построенных на катетах. Идея данного доказательства дополнительно проиллюстрирована с помощью анимации, расположенной выше.

Данное доказательство также получило название «Пифагоровы штаны».

Доказательство Леонардо да Винчи

Главные элементы доказательства — симметрия и движение.

Рассмотрим чертёж, как видно из симметрии, отрезок рассекает квадрат на две одинаковые части (так как треугольники и равны по построению).

Пользуясь поворотом на 90 градусов против часовой стрелки вокруг точки , мы усматриваем равенство заштрихованных фигур и .

Теперь ясно, что площадь заштрихованной нами фигуры равна сумме половин площадей маленьких квадратов (построенных на катетах) и площади исходного треугольника. С другой стороны, она равна половине площади большого квадрата (построенного на гипотенузе) плюс площадь исходного треугольника. Таким образом, половина суммы площадей маленьких квадратов равна половине площади большого квадрата, а следовательно сумма площадей квадратов, построенных на катетах равна площади квадрата, построенного на гипотенузе.

Доказательство методом бесконечно малых

Следующее доказательство при помощи дифференциальных уравнений часто приписывают известному английскому математику Харди, жившему в первой половине XX века.

Рассматривая чертёж, показанный на рисунке, и наблюдая изменение стороны a, мы можем записать следующее соотношение для бесконечно малых приращений сторон с и a (используя подобие треугольников):

Пользуясь методом разделения переменных, находим

Более общее выражение для изменения гипотенузы в случае приращений обоих катетов

Интегрируя данное уравнение и используя начальные условия, получаем

Таким образом, мы приходим к желаемому ответу

Как нетрудно видеть, квадратичная зависимость в окончательной формуле появляется благодаря линейной пропорциональности между сторонами треугольника и приращениями, тогда как сумма связана с независимыми вкладами от приращения разных катетов.

Более простое доказательство можно получить, если считать, что один из катетов не испытывает приращения (в данном случае катет ). Тогда для константы интегрирования получим

Вариации и обобщения

Подобные геометрические фигуры на трех сторонах

Обобщение теоремы Пифагора сделал Евклид в своей работе Начала, расширив площади квадратов на сторонах до площадей подобных геометрических фигур [9] :

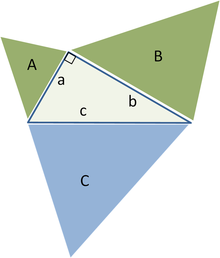
Если построить подобные геометрические фигуры (см. Евклидова геометрия) на сторонах прямоугольного треугольника, тогда сумма двух меньших фигур будет равняться площади большей фигуры.

Главная идея этого обобщения заключается в том, что площадь подобной геометрической фигуры пропорциональна квадрату любого своего линейного размера и в частности квадрату длины любой стороны. Следовательно, для подобных фигур с площадями A, B и C построенных на сторонах с длиной a, b и c, имеем:

Теорема косинусов

Теорема Пифагора — это частный случай более общей теоремы косинусов, которая связывает длины сторон в произвольном треугольнике: [10]

где θ — угол между сторонами a и b.

Если θ равен 90 градусов, тогда cosθ = 0 и формула упрощается до обычной теоремы Пифагора.

Произвольный треугольник

В любой выбранный угол произвольного треугольника со сторонами a, b, c впишем равнобедренный треугольник таким образом, чтобы равные углы при его основании θ равнялись выбранному углу. Предположим, что выбранный угол θ расположен напротив стороны, обозначенной c. В результате мы получили треугольник ABD с углом θ, что расположен напротив стороны a и стороны r. Второй треугольник образуется углом θ, что расположен напротив стороны b и стороны с длиной s, как показано на рисунке. Сабит Ибн Курра [12] утверждал, что стороны в этих трех треугольниках связаны следующим образом: [13] [14]

Когда угол θ приближается к π/2, основание равнобедренного треугольника уменьшается, и две стороны r и s перекрывают друг друга все меньше и меньше. Когда θ = π/2, ADB превращается в прямоугольный треугольник, r + s = c и получаем начальную теорему Пифагора.

Рассмотрим один из доводов. Треугольник ABC имеет такие же углы, как и треугольник ABD, но в обратном порядке. (Два треугольника имеют общий угол при вершине B, оба имеют угол θ и также имеют одинаковый третий угол, по сумме углов треугольника) Соответственно, ABC — подобен отражению ABD треугольника DBA, как показано на нижнем рисунке. Запишем соотношение между противоположными сторонами и прилегающими к углу θ,

Так же отражение другого треугольника,

Перемножим дроби и добавим эти два соотношения:

что и требовалось доказать.

Обобщение для произвольных треугольников через параллелограммы

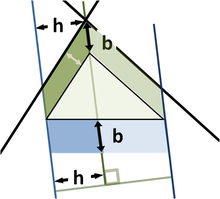
Сделаем дальнейшее обобщение для непрямоугольных треугольников, используя параллелограммы на трех сторонах вместо квадратов. [15] (квадраты — частный случай.) Верхний рисунок демонстрирует, что для остроугольного треугольника площадь параллелограмма на длинной стороне равна сумме параллелограммов на двух других сторонах, при условии что параллелограмм на длинной стороне построен, как изображено на рисунке (размеры, отмеченные стрелками, одинаковые и определяют стороны нижнего параллелограмма). Эта замена квадратов параллелограммами имеет четкое сходство с начальной теоремой Пифагора, считается, что её сформулировал Папп Александрийский в 4 г. н. э. [15]

Нижний рисунок показывает ход доказательства. Посмотрим на левую сторону треугольника. Левый зеленый параллелограмм имеет такую же площадь, как левая часть синего параллелограмма, потому что они имеют такое же основание b и высоту h. Кроме того, левый зеленый параллелограмм имеет такую же площадь, как левый зеленый параллелограмм на верхнем рисунке, потому что они имеют общее основание (верхняя левая сторона треугольника) и общую высоту, перпендикулярную к этой стороне треугольника. Аналогично рассуждая для правой стороны треугольника докажем, что нижний параллелограмм имеет такую же площадь, как у двух зеленых параллелограммов.

Комплексные числа

Теорему Пифагора используют, чтобы найти расстояние между двумя точками в декартовой координатной системе, и эта теорема справедлива для всех истинных координат: расстояние s между двумя точками (a, b) и (c, d) равно

Тем не менее, для операций с векторами с комплексными координатами необходимо провести определенное усовершенствование формулы Пифагора. Расстояние между точками с комплексными числами (a, b) и (c, d); a, b, c, и d все комплексные, сформулируем используя абсолютные величины. Расстояние s основано на векторной разнице (a − c, b − d) в следующем виде: [16] пусть разница a − c = p + i q, где p — действительная часть разницы, q — мнимая часть, и i = √(−1). Аналогично, пусть b − d = r + is. Тогда:

Модуль определен следующим образом:

Стереометрия

Значительным обобщением теоремы Пифагора для трехмерного пространства является теорема де Гуа, названная в честь Ж.-П. де Гуа: если тетраэдр имеет прямой угол (как в кубе), тогда квадрат площади грани, лежащей напротив прямого угла, равен сумме квадратов площадей других трех граней. Этот вывод может быть обобщен как «n-мерная теорема Пифагора»: [18]

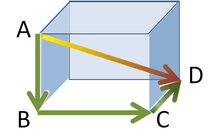
Другое обобщение: Теорема Пифагора может быть применена для стереометрии в следующем виде. Рассмотрим прямоугольный параллелепипед, как показано на рисунке. Найдем длину диагонали BD по теореме Пифагора:

где три стороны образуют прямоугольный треугольник. Используем горизонтальную диагональ BD и вертикальное ребро AB, чтобы найти длину диагонали AD, для этого снова используем теорему Пифагора:

или, если все записать одним уравнением:

Этот результат — это трехмерное выражение для определения величины вектора v (диагональ AD), выраженного через его перпендикулярные составляющие <v_k> (три взаимно перпендикулярные стороны):

Это уравнение можно рассматривать как обобщение теоремы Пифагора для многомерного пространства. Однако, результат на самом деле есть не что иное, как неоднократное применение теоремы Пифагора к последовательности прямоугольных треугольников в последовательно перпендикулярных плоскостях.

Векторное пространство

В случае ортогональной системы векторов имеет место равенство, которое тоже называют теоремой Пифагора:

Если — это проекции вектора на координатные оси, то эта формула совпадает с расстоянием Евклида — и означает, что длина вектора равна корню квадратному суммы квадратов его компонентов.

Аналог этого равенства в случае бесконечной системы векторов имеет название равенства Парсеваля.

Неевклидова геометрия

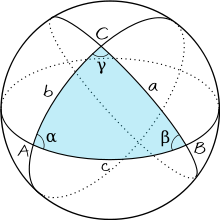
Рассмотрим здесь два случая неевклидовой геометрии — сферическая и гиперболическая геометрия; в обоих случаях, как и для евклидова пространства для прямоугольных треугольников, результат, который заменяет теорему Пифагора, следует из теоремы косинусов.

Однако, теорема Пифагора остается справедливой для гиперболической и эллиптической геометрии, если требование о прямоугольности треугольника заменить условием, что сумма двух углов треугольника должна равняться третьему, скажем A+B = C. Тогда соотношение между сторонами выглядит так: сумма площадей кругов с диаметрами a и b равна площади круга с диаметром c. [22]

Сферическая геометрия

Для любого прямоугольного треугольника на сфере радиусом R (например, если угол γ в треугольнике прямой) со сторонами a, b, c соотношение между сторонами будет иметь такой вид: [23]

Это равенство может быть выведено как особый случай сферической теоремы косинусов, которое справедливо для всех сферических треугольников:

Применяя ряд Тейлора в функции косинуса cos x ≈ 1 − x 2 /2 можно показать, что если радиус R приближается к бесконечности, а аргументы a/R, b/R и c/R приближаются к нулю, сферическое соотношение между сторонами в прямоугольном треугольнике приближается к теореме Пифагора. Подставим приближенные значения для каждого косинуса:

Перемножим выражения в скобках, получим теорему Пифагора для больших радиусов R:

где «higher order terms» — слагаемые высшего порядка, которыми можно пренебречь при больших значениях R.

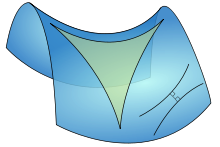
Гиперболическая геометрия

Для прямоугольного треугольника в гиперболической геометрии со сторонами a, b, c, если сторона c расположена напротив прямого угла, соотношение между сторонами будет такое [24]

где cosh — это гиперболический косинус. Эта формула является частным случаем гиперболической теоремы косинусов, которая справедлива для всех треугольников: [25]

где γ — это угол, вершина которого противоположна стороне c.

Дифференциальная геометрия

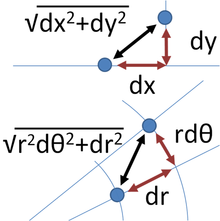
В трехмерном пространстве для двух точек, удаленных друг от друга на бесконечно малое расстояние, запишем теорему Пифагора:

где ds — это расстояние между точками, а (dx, dy, dz) — компоненты вектора, соединяющие эти две точки. Такое пространство называется евклидовым. Однако, обобщение этого выражения пригодно для общих координат (не только декартовых) и общих пространств (не только евклидовых) и имеет вид: [26]

где g_ij называется метрическим тензором. Он может быть функцией позиции. Такие криволинейные пространства включают Риманову геометрию как общий пример. Это формулировка также подходит для Евклидова пространства при применении криволинейных координат. Например, для полярных координат:

Векторное произведение

Теорема Пифагора связывает два выражения величины векторного произведения. Один из подходов к определению векторного произведения требует, чтобы он удовлетворял уравнению: [27]

в этой формуле используется скалярное произведение. Правая сторона уравнения называется детерминант Грамма для a и b, что равно площади параллелограмма, образованного этими двумя векторами. Исходя из этого требования, а также требования о перпендикулярности векторного произведения к его составляющим a и b следует, что, за исключением тривиальных случаев из 0- и 1-мерного пространства, векторное произведение определено только в трех и семи измерениях. [28] Используем определение угла в n-мерном пространстве: [29]

это свойство векторного произведения дает его величину в таком виде:

Через фундаментальное тригонометрическое тождество Пифагора [30] получаем другую форму записи его величины:

Альтернативный подход к определению векторного произведения использует выражение для его величины. Тогда, рассуждая в обратном порядке, получаем связь со скалярным произведением:

Источник