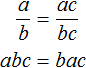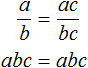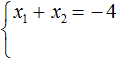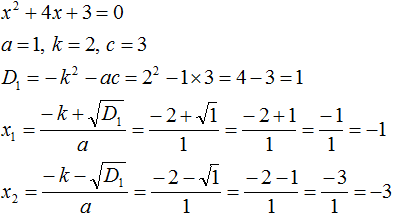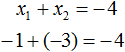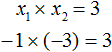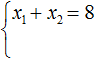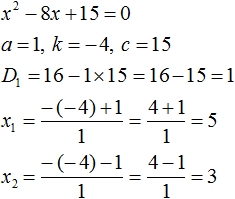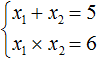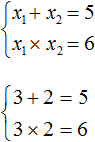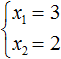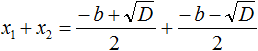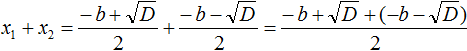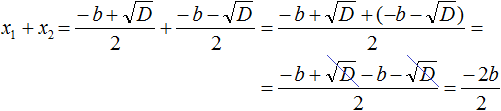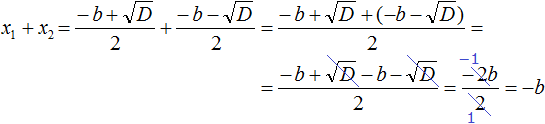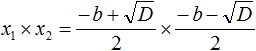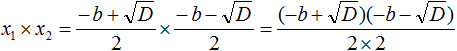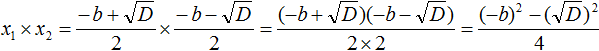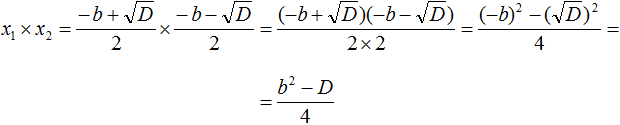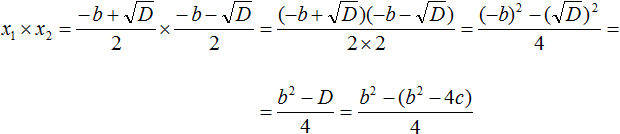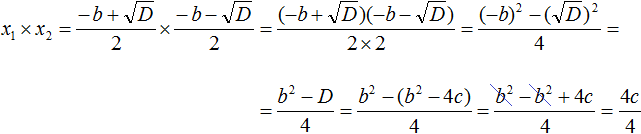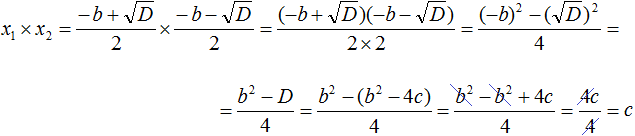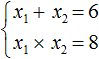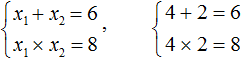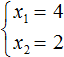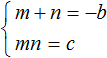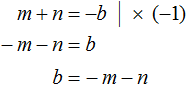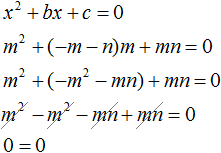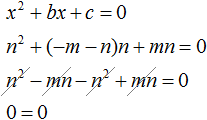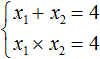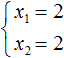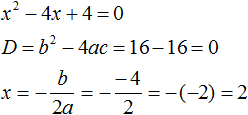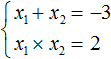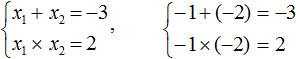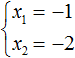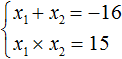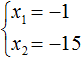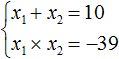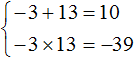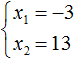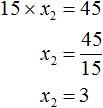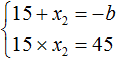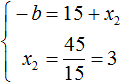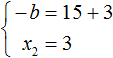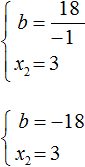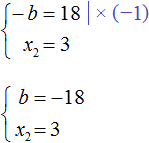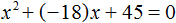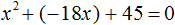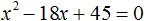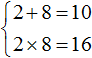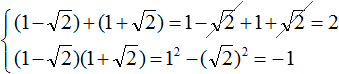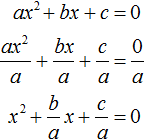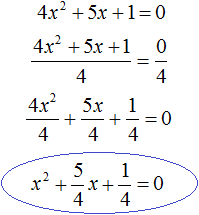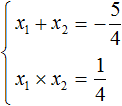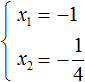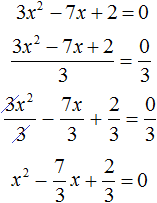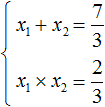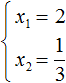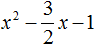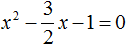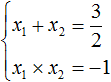Теорема виета что это
Теорема Виета
После того, как вы внимательно изучите, как решать квадратные уравнения обычным образом с помощью формулы для корней можно рассмотреть другой способ решения квадратных уравнений — с помощью теоремы Виета.
Перед тем, как изучить теорему Виета, хорошо потренируйтесь в определении коэффициентов « a », « b » и « с » в квадратных уравнениях. Без этого вам будет трудно применить теорему Виета.
Когда можно применить теорему Виета
Не ко всем квадратным уравнениям имеет смысл использовать эту теорему. Применять теорему Виета имеет смысл только к приведённым квадратным уравнениям.
Приведенное квадратное уравнение — это уравнение, в котором старший коэффициент « a = 1 ». В общем виде приведенное квадратное уравнение выглядит следующим образом:
Обратите внимание, что разница с обычным общим видом квадратного уравнения « ax 2 + bx + c = 0 » в том, что в приведённом уравнении « x 2 + px + q = 0 » коэффициент « а = 1 ».
Если сравнить приведенное квадратное уравнение « x 2 + px + q = 0 » с обычным общим видом квадратного уравнения « ax 2 + bx + c = 0 », то становится видно,
что « p = b », а « q = c ».
Теперь давайте на примерах разберем, к каким уравнениям можно применять теорему Виета, а где это не целесообразно.
Так как « a = 1 » можно использовать теорему Виета.
Приведем уравнение к общему виду:
Так как « a = 3 » не следует использовать теорему Виета.
Приведем уравнение к общему виду:
Так как « a = −1 » не следует использовать теорему Виета.
Как использовать теорему Виета
Теперь мы готовы перейти к самому методу Виета для решения квадратных уравнений.
Теорема Виета для приведённых квадратных уравнений « x 2 + px + q = 0 » гласит что справедливо следующее:
Чтобы было проще запомнить формулу Виета, следует запомнить:
«Коэффициент « p » — значит плохой, поэтому он берется со знаком минус ».
Так как в этом уравнении « a = 1 », квадратное уравнение считается приведённым, значит, можно использовать метод Виета. Выпишем коэффициенты « p » и « q ».
Запишем теорему Виета для квадратного уравнения.
| x1 + x2 = − 4 |
| x1 · x2 = −5 |
Методом подбора мы приходим к тому, что корни уравнения « x1 = −5 » и « x2 = 1 ». Запишем ответ.
Рассмотрим другой пример.
Старший коэффициент « a = 1 » поэтому можно применять теорему Виета.
| x1 + x2 = − 1 |
| x1 · x2 = −6 |
Методом подбора получим, что корни уравнения « x1 = −3 » и « x2 = 2 ». Запишем ответ.
Если у вас не получается решить уравнение с помощью теоремы Виета, не отчаивайтесь. Вы всегда можете решить любое квадратное уравнение, используя формулу для нахождения корней.
Деление уравнение на первый коэффициент
Рассмотрим уравнение, которое по заданию требуется решить, используя теорему Виета.
Сейчас в уравнении « a = 2 », поэтому перед тем, как использовать теорему Виета нужно сделать так, чтобы « a = 1 ».
Для этого достаточно разделить все уравнение на « 2 ». Таким образом, мы сделаем квадратное уравнение приведённым.
Теперь « a = 1 » и можно смело записывать формулу Виета и находить корни методом подбора.
| x1 + x2 = − (−8) |
| x1 · x2 = −9 |
| x1 + x2 = 8 |
| x1 · x2 = −9 |
Методом подбора получим, что корни уравнения « x1 = 9 » и « x2 = −1 ». Запишем ответ.
Бывают задачи, где требуется найти не только корни уравнения, но и коэффициенты самого уравнения. Например, как в такой задаче.
Корни « x1 » и « x2 » квадратного уравнения « x 2 + px + 3 = 0 » удовлетворяют условию « x2 = 3x1 ». Найти « p », « x1 », « x2 ».
Запишем теорему Виета для этого уравнения.
По условию дано, что « x2 = 3x1 ». Подставим это выражение в систему вместо « x2».
| x1 + 3x1 = −p |
| x1 · 3x1 = 3 |
| 4x1 = −p |
| 3x1 2 = 3 |(:3) |
| 4x1 + p = 0 |
| x1 2 = 1 |
| p = −4x1 |
| x1 2 = 1 |
Решим полученное квадратное уравнение « x1 2 = 1 » методом подбора и найдем « x1 ».
Мы получили два значения « x1 ». Для каждого из полученных значений найдем « p » и запишем все полученные результаты в ответ.
Теорема Виета в общем виде
В школьном курсе математики теорему Виета используют только для приведённых уравнений, где старший коэффициент « a = 1 », но, на самом деле, теорему Виета можно применить к любому квадратному уравнению.
В общем виде теорема Виета для квадратного уравнения выглядит так:
x1 + x2 =
| ||
x1 · x2 =
|
Убедимся в правильности этой теоремы на примере. Рассмотрим неприведённое квадратное уравнение.
Используем для него теорему Виета в общем виде.
x1 + x2 =
| ||
x1 · x2 =
|
| x1 + x2 = −1 |
| x1 · x2 = −6 |
Методом подбора получим, что корни уравнения « x1 = −3 » и « x2 = 2 ». Запишем ответ.
В заданиях школьной математики мы не рекомендуем использовать теорему Виета в общем виде.
Другими словами, реальную пользу теорема Виета приносит только для приведённых квадратных уравнений, в которых « a = 1 ». Именно в таких случаях она не усложняет жизнь, а позволят без дополнительных расчетов быстро найти корни.
Теорема Виета.
Формулы Виета — это формулы, которые выражают коэффициенты многочлена через его корни.
Эти формулы хорошо использовать для сверки правильности определения корней многочлена. Еще их
используют для выведения многочлена из заданных корней.
С помощью теоремы Виета решаются квадратные уравнения.
Если наибольший коэффициент многочлена 
использования формулы Виета нужно сначала поделить все коэффициенты на 
значении корней многочлена). В таком случае формулы Виета дают выражение для отношений всех
коэффициентов к наибольшему.
Формулировка теоремы Виета для квадратного трехчлена.
Для приведенного квадратного уравнения (такого, коэффициент при x 2 в котором = 1): сумма корней
приведённого квадратного уравнения 

произведение корней = свободному члену 
В общем случае – для не приведённого квадратного уравнения:
Пользуясь этой теоремой, легко находить корни некоторых квадратных уравнений в уме.
Смысл теоремы Виета состоит в том, что, не зная корней квадратного трехчлена, запросто можно вычислить
их сумму и произведение – простейшие симметричные многочлены от двух переменных 

Теорема Виета дает угадывать целые корни квадратного трехчлена.
Обратная теорема Виета.
Если числа 


квадратному уравнению 
Даны числа 

Предположим наше квадратное уравнение выглядит так:
Значит, согласно теореме Виета, его коэффициенты связаны с корнями таким соотношениями:
Таким образом квадратное уравнение:
Ответ:
Общая формулировка теоремы Виета.
Если 

соответствующее их кратности количество раз), то коэффициенты 
симметрических многочленов от корней, как показано ниже:
Другими словами, произведение 

Теорема Виета
Что называют теоремой?
Если человек обнаружил в математике какую-нибудь закономерность, позволяющую быстро решить ту или иную задачу, то ему не следует говорить о том, что он сделал открытие. Потому что может случиться так, что эта закономерность работает только для определённых случаев, а для других не работает или вовсе решает задачу неправильно.
Чтобы поделиться своим открытием с другими людьми, найденную закономерность следует сформулировать в виде утверждения, а затем доказать это утверждение, приводя неоспоримые факты.
Сформулированное утверждение называют теоремой. А доказательство теоремы состоит из фактов, логических рассуждений и вычислений, которые не оспариваются.
Например, теоремой можно назвать следующее утверждение:
«Если числитель и знаменатель обыкновенной дроби умнóжить на какое-нибудь число, то значение данной дроби не измéнится».
А затем привести такое доказательство:
Для доказательства этого равенства воспользуемся основным свойством пропорции:
От перестановки мест сомножителей произведение не меняется. Поэтому в получившемся равенстве можно упорядочить правую часть по алфавиту:
Поскольку равенство 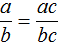

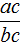
Теорема Виета
Французский математик Франсуа Виет выявил интересную взаимосвязь между коэффициентами приведённого квадратного уравнения и корнями этого же уравнения. Эта взаимосвязь представлена в виде теоремы и формулируется так:
Сумма корней приведённого квадратного уравнения x 2 + bx + c = 0 равна второму коэффициенту, взятому с противоположным знáком, а произведение корней равно свободному члену.
Знак системы (фигурная скобка) говорит о том, что значения x1 и x2 удовлетворяют обоим равенствам.
Значит выражение 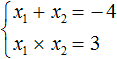
Значит выражение 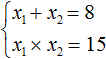
Замечание. Чтобы теорема Виета выполнялась, квадратное уравнение обязательно должно быть приведённым и иметь корни.
А значит записывать выражение 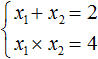
Теорема Виета полезна тем, что позволяет до начала решения узнать знаки корней уравнения.
Например, запишем для уравнения x 2 − 5x + 6 = 0 сумму и произведение его корней. Сумма корней равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:
Доказательство теоремы Виета
Вспомним формулы корней квадратного уравнения:
Запишем правую часть в виде дроби с одним знаменателем:
Раскроем скобки в числителе и приведём подобные члены:
Подставим вместо x1 и x2 соответствующие выражения из формул корней квадратного уравнения. Не забываем, что коэффициент a всё ещё равен единице:
Чтобы перемнóжить дроби, нужно перемнóжить их числители и знаменатели:
В получившемся выражении раскроем скобки в числителе и приведём подобные члены:
Сократим получившуюся дробь на 4
Таким образом, сумма корней приведённого квадратного уравнения x 2 + bx + c = 0 равна второму коэффициенту, взятому с противоположным знáком ( x1 + x2 = −b ), а произведение корней равно свободному члену ( x1 × x2 = c ). Теорема доказана.
Теорема, обратная теореме Виета
Когда записана сумма и произведение корней приведённого квадратного уравнения, обычно начинается подбор подходящих корней к этому уравнению. В этот момент в работу включается так называемая теорема, обратная теореме Виета. Она формулируется так:
Если числа x1 и x2 таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знáком, а произведение чисел x1 и x2 равно свободному члену уравнения x 2 + bx + c = 0, то числа x1 и x2 являются корнями уравнения x 2 + bx + c = 0.
Обратные теоремы бывают поставлены так, что их утверждением является заключение первой теоремы.
Ранее мы решили уравнение x 2 − 5x + 6 = 0 и написали для него такую сумму и произведение корней:
Пример 2. Решить квадратное уравнение x 2 − 6x + 8 = 0 по теореме, обратной теореме Виета.
Число 8 можно получить если перемножить числа 4 и 2 либо 1 и 8.
Если числа m и n таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знáком, а произведение чисел m и n равно свободному члену уравнения x 2 + bx + c = 0, то числа m и n являются корнями уравнения x 2 + bx + c = 0
Видим, что при x = n тоже получается верное равенство. Значит число n является корнем уравнения.
Примеры решения уравнений по теореме, обратной теореме Виета
Пример 1. Решить квадратное уравнение x 2 − 4x + 4 = 0 по теореме, обратной теореме Виета.
Запишем сумму корней x1 и x2 и приравняем её к второму коэффициенту, взятому с противоположным знаком. Также запишем произведение корней x1 и x2 и приравняем его к свободному члену :
Данный пример показывает, что теорема обратная теореме Виета, работает и для уравнений, имеющих только один корень. Признаком того, что квадратное уравнение имеет только один корень является то, что значения x1 и x2 совпадают.
Пример 2. Решить уравнение x 2 + 3x + 2 = 0 по теореме, обратной теореме Виета.
Запишем сумму и произведение корней данного уравнения:
Сумма бывает отрицательной если оба слагаемых отрицательны либо отрицательным является одно слагаемое, модуль которого больше.
Очевидно, что корнями являются два отрицательных числа. Произведение отрицательных чисел есть положительное число. А сумма отрицательных чисел есть отрицательное число.
Итак, корнями являются числа −1 и −2
Пример 3. Решить уравнение x 2 + 16x + 15 = 0 по теореме, обратной теореме Виета.
Запишем сумму и произведение корней данного уравнения:
Как и в прошлом примере сумма корней равна отрицательному числу, а произведение корней — положительному числу.
Произведение бывает положительным если оба сомножителя положительны либо оба сомножителя отрицательны. Первый вариант отпадает сразу, поскольку сумма корней равна отрицательному числу. Тогда получается, что оба корня будут отрицательными. Попробуем подобрать их.
Пример 4. Решить уравнение x 2 − 10x − 39 = 0 по теореме, обратной теореме Виета.
Запишем сумму и произведение корней данного уравнения:
Значит корнями уравнения x 2 − 10x − 39 = 0 являются числа −3 и 13
По теореме Виета произведение корней приведённого квадратного уравнения равно свободному члену. В данном случае это произведение равно 45
Этот второй корень также можно было бы получить, выразив из равенства 15 × x2 = 45 переменную x2
По теореме Виета сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком. Если сумма корней равна 18, а 18 это положительное число, то в самóм уравнении этот коэффициент будет отрицательным:
Обычно решение к такой задаче записывают так. Сначала записывают основную теорему Виета в виде суммы и произведения корней:
Из этой системы мы видим, что x2 равно 3. Подставим его в первое равенство:
Теперь из первого равенства мы видим, что −b равно 18
Этот же результат можно получить если в выражении 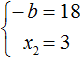
Теперь возвращаемся к исходному уравнению x 2 + bx + 45 = 0 и подставляем найденное значение b
Запишем сумму и произведение корней:
Пример 7. Используя теорему Виета, написать приведённое квадратное уравнение, корнями которых являются числа 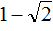
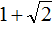
Запишем сумму и произведение корней:
Сумма корней равна 2. Тогда в уравнении второй коэффициент будет равен −2. А произведение корней равно −1. Значит свободный член будет равен −1. Тогда:
Когда квадратное уравнение неприведённое
Теорема Виета выполняется только тогда, когда квадратное уравнение является приведённым.
Получилось уравнение 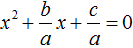


Получили приведённое квадратное уравнение. В нём второй коэффициент равен 

Отсюда методом подбора находим корни −1 и
Возможно этот метод вы редко будете использовать при решении квадратных уравнений. Но знать о нём не помешает.
Пример 2. Решить квадратное уравнение 3x 2 − 7x + 2 = 0
Данное уравнение не является приведённым, а значит его пока нельзя решить по теореме, обратной теореме Виета.
Сделаем данное уравнение приведенным. Разделим обе части на коэффициент, который располагается перед x 2
Получили уравнение 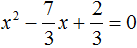
Отсюда методом подбора находим корни 2 и
Пример 3. Решить квадратное уравнение 2x 2 − 3x − 2 = 0
Прирáвниваем получившееся выражение к нулю:
Теперь применяем теорему Виета. Сумма корней будет равна второму коэффициенту, взятому с противоположным знáком, а произведение корней свободному члену:
Отсюда методом подбора находим корни 2 и