Точка триангуляции что это

Триангуляция

Полезное

Смотреть что такое «Триангуляция» в других словарях:

ТРИАНГУЛЯЦИЯ — (позд. лат., от лат. triangalus треугольник.). Тригонометрическое действие, при посредстве которого снимают план с известной местности, разделивши ее на треугольники, которые вычисляются при помощи тригонометрических формул. Словарь иностранных… … Словарь иностранных слов русского языка

Триангуляция — (геодезия) один из методов создания сети опорных геодезических пунктов и сама сеть. В математике Триангуляция (топология) разбиение топологического пространства на симплексы. Триангуляция Делоне … Википедия

Триангуляция — (от лат. triangulum треугольник * a. triangulation, survey by triangulation; н. Triangulation; ф. triangulation; и. tciangulacion) один из методов создания сети опорных геодезич. пунктов, заключающийся в построении рядов или сетей из… … Геологическая энциклопедия

ТРИАНГУЛЯЦИЯ — ТРИАНГУЛЯЦИЯ, см. тригонометрия. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля

триангуляция — Метод построения геодезической сети в виде треугольников, в которых измерены их углы и некоторые из сторон [ГОСТ 22268 76] триангуляция Метод определения планового положения геодезических пунктов путём построения на местности системы смежных или… … Справочник технического переводчика

ТРИАНГУЛЯЦИЯ — (от лат. triangulum треугольник) метод определения положения геодезических пунктов построением на местности систем смежно расположенных треугольников, в которых измеряют длину одной стороны (по базису) и углы, а длины других сторон получают… … Большой Энциклопедический словарь

ТРИАНГУЛЯЦИЯ — (тригонометрическая съемка), в навигации и топографической съемке метод определения расстояния. Площадь съемки делится на треугольники. Затем ТЕОДОЛИТОМ измеряют основание треугольника и прилежащие углы. Расстояния от концов основания до… … Научно-технический энциклопедический словарь

ТРИАНГУЛЯЦИЯ — ТРИАНГУЛЯЦИЯ, триангуляции, мн. нет, жен. (от лат. triangulus треугольник). 1. Вычисление углов и протяжений методами тригонометрии (мат.). 2. Определение взаимного расположения точек на поверхности при помощи построения сети треугольников… … Толковый словарь Ушакова

ТРИАНГУЛЯЦИЯ — (Triangulation) наиболее точный прием определения взаимного расположения точек на земной поверхности. При Т. выбираются на открытых и возвышенных местах опорные пункты и закрепляются постройкой специальных знаков. Стороны между знаками образуют… … Морской словарь

ТРИАНГУЛЯЦИЯ — горизонтальная съемка расположения вершин сети треугольников путем измерения длины одной стороны базиса и измерения всех углов. Т. применяется для точной съемки больших участков земной поверхности или для определения длины дуги меридиана или… … Технический железнодорожный словарь

триангуляция — сущ., кол во синонимов: 2 • аэротриангуляция (1) • стереотриангуляция (1) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов

Источник

Алгоритм триангуляции Делоне методом заметающей прямой

Доброго времени суток!

В этой статье я подробно опишу алгоритм, который у меня получился в результате использования идеи «заметающей прямой» для построения триангуляции Делоне на плоскости. В нем есть несколько идей, которые я нигде не встречал, когда читал статьи про триангуляцию.
Возможно, кто-то тоже найдет их необычными. Я постараюсь сделать все в лучших традициях и включить в рассказ следующие вещи: описание используемых структур данных, описание шагов алгоритма, доказательство корректности, временные оценки, а также сравнение с итеративным алгоритмом, использующим kD-дерево.

Определения и постановка задачи

Триангуляция

Говорят, что на множестве точек на плоскости задана триангуляция, если некоторые пары точек соединены ребром, любая конечная грань в получившемся графе образует треугольник, ребра не пересекаются, и граф максимален по количеству ребер.

Триангуляция Делоне

Триангуляцией Делоне называется такая триангуляция, в которой для любого треугольника верно, что внутри описанной около него окружности не находится точек из исходного множества.

Замечание: для заданного множества точек, в котором никакие 4 точки не находятся на одной окружности, существует ровно одна триангуляция Делоне.

Условие Делоне

Пусть на множестве точек задана триангуляция. Будем говорить, что некоторое подмножество точек удовлетворяет условию Делоне, если триангуляция, ограниченная на это подмножество, является триангуляцией Делоне для него.

Критерий для триангуляции Делоне

Выполнение условия Делоне для всех точек, образующих четырехугольник в триангуляции, эквивалентно тому, что данная триангуляция является триангуляцией Делоне.

Замечание: для невыпуклых четырехугольников условие Делоне всегда выполнено, а для выпуклых четырехугольников (вершины которого не лежат на одной окружности) существует ровно 2 возможные триангуляции (одна из которых является триангуляцией Делоне).

Задача заключается в том, чтобы для заданного множества точек построить триангуляцию Делоне.

Описание алгоритма

Видимые точки и видимые ребра

Пусть задана минимальная выпуклая оболочка (далее МВО) конечного множества точек (ребра, соединяющие некоторые из точек так, чтобы они образовывали многоугольник, содержащий все точки множества) и точка A, лежащая вне оболочки. Тогда точка плоскости называется видимой для точки А, если отрезок, соединяющий ее с точкой А, не пересекает МВО.

Ребро МВО называется видимым для точки А, если его концы видимы для А.

На следующей картинке красным помечены ребра, видимые для красной точки:

Замечание: контур триангуляции Делоне является МВО для точек, на которых построена.

Замечание 2: в алгоритме видимые для добавляемой точки А ребра образуют цепочку, то есть несколько подряд идущих ребер МВО

Хранение триангуляции в памяти

Есть некоторые стандартные способы, неплохо описанные в книге Скворцова [1]. Ввиду специфики алгоритма, я предложу свой вариант. Так как хочется проверять 4-угольники на условие Делоне, то рассмотрим их строение. Каждый 4-угольник в триангуляции представляет из себя 2 треугольника, имеющих общее ребро. У каждого ребра есть ровно 2 треугольника, прилегающих к нему. Таким образом, каждый четырехугольник в триангуляции порождается ребром и двумя вершинами, находящимися напротив ребра в прилегающих треугольниках.
Так как по ребру и двум вершинам восстанавливаются два треугольника и их смежность, то по всем таким структурам мы сможем восстановить триангуляцию. Соответственно предлагается хранить ребро с двумя вершинами в множестве и выполнять поиск по ребру (упорядоченной паре вершин).

Алгоритм

Идея заметающей прямой заключается в том, что все точки сортируются по одному направлению, а затем по очереди обрабатываются.

Проверка условия Делоне

Способы проверки четырехугольников на условие Делоне можно найти в той же книжке [1]. Подмечу лишь, что при выборе метода с тригонометрическими функциями оттуда при неаккуратной реализации могут получаться отрицательные значения синусов, есть смысл брать их по модулю.

Поиск видимых ребер

Осталось понять, как эффективно находить видимые ребра. Заметим, что предыдущая добавленная точка S находится в МВО на текущей итерации, так как имеет наибольшую координату , а также видима для текущей точки. Тогда, замечая, что концы видимых ребер образуют непрерывную цепочку видимых точек, мы можем идти от точки S в обе стороны по МВО и собирать ребра, пока они видимы (видимость ребра проверяется с помощью векторного произведения). Таким образом удобно хранить МВО как двусвязный список, на каждой итерации удаляя видимые ребра и добавляя 2 новых из рассматриваемой точки.

Визуализация работы алгоритма

Две красные точки — добавляемая и предыдущая. Красные ребра в каждый момент составляют стек рекурсии из шага (4):

Корректность алгоритма

Чтобы доказать корректность алгоритма, достаточно доказать сохранение инварианта в шагах (3) и (4).

Шаг (3)

После шага (3), очевидно, получится некоторая триангуляция текущего множества точек.

Шаг (4)

В процессе выполнения шага (4) все четырехугольники, не удовлетворяющие условию Делоне, находятся в стеке рекурсии (следует из описания), а значит, по окончании шага (4) все четырехугольники удовлетворяют условию Делоне, то есть действительно построена триангуляция Делоне. Тогда осталось доказать, что процесс в шаге (4) когда-нибудь закончится. Это следует из того, что все ребра, добавленные при перестроении, исходят из текущей рассматриваемой вершины (то есть на шаге их не больше, чем ) и из того, что после добавления этих ребер мы не будем рассматривать четырехугольники, порожденные ими (см. предыдущее замечание), а значит, добавим не более одного раза.

Временная сложность

В среднем на равномерном, нормальном распределениях алгоритм работает довольно неплохо (результаты приведены ниже в табличке). Есть предположение, что время его работы составляет . В худшем случае имеет место оценка .

Давайте разберем время работы по частям и поймем, какая из них оказывает самое большое влияние на итоговое время:

Сортировка по направлению

Для сортировки будем использовать оценку .

Поиск видимых ребер

Для начала покажем, что время, суммарно затраченное на поиск видимых ребер, есть . Заметим, что на каждой итерации мы находим все видимые ребра и еще 2 (первые не видимые) за линейное время. В шаге (3) мы добавляем в МВО новые 2 ребра. Таким образом, всего в меняющейся на протяжении алгоритма МВО побывает не более ребер, значит, и различных видимых ребер будет не более . Еще мы найдем ребер, не являющихся видимыми. Таким образом, в общей сложности найдется не более ребер, что соответствует времени .

Построение новых треугольников

Суммарное время на построение треугольников из шага (3) с уже найденными видимыми ребрами, очевидно, .

Перестроение триангуляции

Осталось разобраться с шагом (4). Сначала заметим, что проверка условия Делоне и перестроение в случае его не выполнения являются довольно дорогими действиями (хоть и работают за ). Только на проверку условия Делоне может уйти около 28 арифметических операций. Посмотрим на среднее количество перестроений в течение этого шага. Практические результаты на некоторых распределениях приведены ниже. По ним очень хочется сказать, что среднее количество перестроений растет с логарифмической скоростью, однако оставим это как лишь предположение.

Здесь еще хочется подметить, что от направления, вдоль которого производится сортировка, может сильно варьироваться среднее число перестроений на точку. Так на миллионе равномерно распределенных на длинном низком прямоугольнике с отношением сторон 100000:1 это число варьируется от 1.2 до 24 (эти значения достигаются при сортировке данных по горизонтали и вертикали соответственно). Поэтому я вижу смысл выбирать направление сортировки произвольным образом (в данном примере при произвольном выборе в среднем получалось около 2 перестроений) или выбрать его вручную, если данные заранее известны.

Таким образом, основное время работы программы обычно уходит на шаг (4). Если же он выполняется быстро, то есть смысл задуматься над ускорением сортировки.

Худший случай

В худшем случае на -ой итерации происходит рекурсивный вызов в шаге (4), то есть, суммируя по всем i, получаем асимптотику в худшем случае . Следующая картинка иллюстрирует красивый пример, на котором программа может работать долго (1100 перестроений в среднем при добавлении новой точки при входных данных в 10000 точек).

Сравнение с итеративным алгоритмом построения триангуляции Делоне с использованием kD-дерева

Описание итеративного алгоритма

Коротко опишу вышеуказанный алгоритм. При поступлении очередной точки мы с помощью kD-дерева (советую почитать про него где-нибудь, если вы не знаете) находим довольно близкий к ней уже построенный треугольник. Затем обходом в глубину ищем треугольник, в который попадает сама точка. Достраиваем ребра в вершины найденного треугольника и фактически выполняем шаг (4) из нашего алгоритма для новых четырехугольников. Так как точка может быть вне триангуляции, то для упрощения предлагается накрыть все точки большим треугольником (построить его заранее), это решит проблему.

Сходство алгоритмов

Различия алгоритмов

В итеративном алгоритме локализация точки (поиск нужного треугольника) происходит в среднем за , на вышеуказанных распределениях в среднем происходит 3 перестроения (как показано в [1]) при условии произвольного порядка подачи точек. Таким образом заметающая прямая выигрывает время у итеративного алгоритма в локализации, но проигрывает его в перестроениях (которые, напомню, довольно тяжелые). Ко всему прочему итеративный алгоритм работает в режиме онлайн, что также является его отличительной особенностью.

Заключение

Здесь я просто покажу некоторые интересные триангуляции, получившиеся в результате работы алгоритма.

Источник

Известно, что триангуляция как геодезический термин означает способ создания геодезических сетей. Да, это так. Но следует начать с другого.

Изначально с возникновением потребности человека в познании, обычное мышление приводит его к накоплению определенного багажа знаний. С развитием научного мышления все эти знания систематизируются, в том числе разъясняются на основе фактов, явлений и доказательств. Применяя теоретические предположения на практике, возникают своего рода критерии истины. То есть имеют ли подтверждения практическим путем все те предположения, которые с помощью определенных способов дают конкретный результат. Пожалуй, одним из таких научных методов, решающих задачу по высокоточному измерению больших расстояний между пунктами на земной поверхности с построением примыкающих друг к другу треугольников и измерений внутри них стал способ триангуляции.

Первым кто изобрел и применил метод триангуляции (1614-1616), был великий голландский ученый Виллеброрд Снелл (Снеллиус). В те годы уже были предположения о том, что Земля является планетой в космическом пространстве и имеет форму сферы (из космологии Джордано Бруно 1548-1600). Установление точных размеров планеты имело большое практическое значение по ее освоению в дальнейшем. Вот для этого в Нидерландах через постройку ряда треугольников были впервые выполнены градусные измерения дуги меридиана способом триангуляции. Что имеется ввиду. Выполнив измерения между жесткими геодезическими пунктами с разностью широт между ними в один градус (у Снеллиуса 1º11´30″) способом триангуляции и получив конкретное расстояние дуги, голландский математик обычным расчетом мог получить длину всей окружности меридиана. Очевидно, что вычислить радиус Земли, приняв ее фигуру за форму шара (эллипса), оставалось делом техники.

В завершение исторического экскурса можно выделить взаимосвязанность и выборность научных познаний для будущего практического применения человеком. И не удивительно, что изобретение способа триангуляции произошло именно в Нидерландах, которые на тот момент считались ведущей морской державой с потребностью новых познаний в навигации, географии, астрономии и конечно геодезии.

Сущность метода

Триангуляция заключается в определении пространственного местоположения специально закрепленных на местности геодезических пунктов в вершинах целого ряда треугольников. Изначально, с высокой степенью точности (до долей секунд) определяют азимуты исходных направлений ab, ba, mn, nm (рис.1.Триангуляционный ряд треугольников по меридиану). Следующим этапом будет определение астрономических координат (широты и долготы) в пунктах измерений азимутов двух исходных базисов. В каждой паре жестких сторон (ab, mn) координаты измеряются только в одной точке, например a, m (рис.1). При этом следует обратить особое внимание на определение астрономических широт в ряду треугольников, расположенных по направлению меридианов. При измерениях в треугольниках, сформированных вдоль параллелей, необходимо уделить должное внимание определению астрономических долгот. Далее производят измерения длин двух базисных сторон (ab, mn). Эти стороны имеют сравнительно не большие длины (порядка 8-10 км). Поэтому их измерения более экономичные и точные относительно сторон cd, tq, составляющих расстояния от 30 до 40 км. В следующую очередь выполняется переход от базисов ab, mn через угловые измерения в ромбах abcd и mntq к сторонам cd, tq. А затем последовательно практически в каждой вершине треугольников cde, def, efg и других измеряются горизонтальные углы до примыкания к следующей основной стороне tq всего ряда треугольников. Через измеренные углы треугольника с измеренной базисной или вычисленной основной стороной последовательно вычисляются все другие стороны, их азимуты и координаты вершин треугольников.

Рис.1. Триангуляционный ряд треугольников по меридиану.

Триангуляционные сети

После первого применения градусного измерения дуги Снеллиусом триангуляционный метод становится основным способом в геодезических высокоточных измерениях. С XIX века, когда триангуляционные работы стали более совершенными с его помощью стали формироваться целые геодезические сети, строящиеся вдоль параллелей и меридианов. Самая знаменитая из всех известна под наименованием геодезической меридианной дуги Струве и Теннера (1816-1852) в последствие зачислена в мировое наследие по ЮНЕСКО. Ее триангуляционный ряд протянулся по Норвегии, Швеции, Финляндии и России от Северного Ледовитого океана до Черного моря в устье Дуная и составил дугу в 25º20´(рис.2).

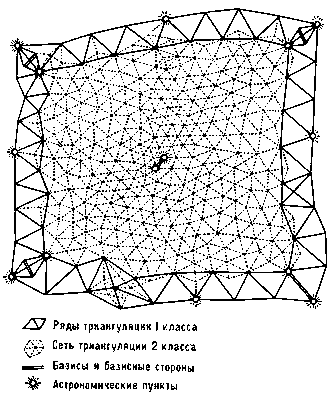
За основу геодезических сетей триангуляции в нашей стране принята схема профессора Ф.Н.Красовского (рис.3). Ее суть заключается в применении принципа построений от общего к частному. Изначально закладываются вдоль меридианов и параллелей пункты, образующие ряды треугольников протяженностью в пределах 200-240 км. Длины сторон в самих треугольниках составляют 25-40км. Все астрономические измерения азимутов, координат (широт и долгот) выходных точек на пунктах Лапласа (1) и промежуточных астрономических точках (2), высокоточные базисные (3) геодезические измерения и в каждой точке этой цепи должно соответствовать установленным требованиям I класса точности (рис.3). Замкнутый полигон из четырех триангуляционных рядов представляет собой фигуру, напоминающую квадрат с периметром равным ориентировочно около 800 км. Через центральные части первоклассных рядов триангуляции устраиваются в направлении друг к другу основные ряды триангуляционной сети II класса (рис.3) соответствующей точности. Базисные длины сторон в этих рядах не измеряются, а принимаются базисы со сторон триангуляции I класса. Аналогично отсутствуют и астрономические пункты. Возникшие четыре пространства заполняются сплошными триангуляционными сетями и II, и III классов.

Рис.3.Государственные сети триангуляции.

Безусловно описанная схема развития сетей триангуляции по Красовскому не может закрыть всю территорию страны ввиду понятных причин больших лесных и не заселенных территорий страны. Поэтому с запада на восток вдоль параллелей были проложены отдельные ряды первоклассной триангуляции и полигонометрии, а не сплошная триангуляционная сеть.

Достоинства триангуляции

В развитии геодезической науки и ее практического применения очевидны достоинства триангуляционного способа измерений. С помощью этого универсального метода возможно:

Источник

Основы геодезии

О геодезии и разный полезный материал для геодезистов.

Понятие о триангуляции

Триангуляция представляет собой группу примыкающих один к другому треугольников, в которых измеряют все три угла; два или более пунктов имеют известные координаты, координаты остальных пунктов подлежат определению. Группа треугольников образует либо сплошную сеть, либо цепочку треугольников.

Координаты пунктов триангуляции как правило вычисляют на ЭВМ по программам, реализующим алгоритмы строгого уравнивания по МНК. На стадии предварительной обработки триангуляции последовательно решают треугольники один за другим. В нашем курсе геодезии мы рассмотрим решение лишь одного треугольника.

В первом треугольнике ABP (рис.2.24) известны координаты двух вершин (A и B) и его решение выполняют в следующем порядке:

Рис.2.24. Единичный треугольник триангуляции

Это уравнение содержит три неизвестных поправки β и решить его можно лишь при наличии двух дополнительных условий.

Эти условия имеют вид:

откуда следует, что

4. Вычисляют исправленные значения углов:

5. Решают обратную задачу между пунктами A и B вычисляют дирекционный угол αAB и длину S3 стороны AB.
6. По теореме синусов находят длины сторон AP и BP:

7. Вычисляют дирекционные углы сторон AP и BP:

8. Решают прямую геодезическую задачу из пункта A на пункт P и для контроля – из пункта B на пункт P; при этом оба решения должны совпасть.

В сплошных сетях триангуляции кроме углов в треугольниках измеряют длины отдельных сторон треугольников и дирекционные углы некоторых направлений; эти измерения выполняются с большей точностью и играют роль дополнительных исходных данных. При уравнивании сплошных сетей триангуляции в них могут возникнуть следующие условия:

Формула для подсчета количества условий в произвольной сети триангуляции имеет вид:

где n – общее количество измеренных углов в треугольниках,
k – число пунктов в сети,
g – количество избыточных исходных данных.

Источник