Три плоских колеса расположены так что попарно
Три плоских колеса расположены так что попарно
Задача 1:
В мешке лежат шарики двух разных цветов: черного и белого. Какое наименьшее число шариков нужно вынуть из мешка вслепую так, чтобы среди них заведомо оказались два шарика одного цвета?
Решение:
Обозначим первое из этих чисел через a. Получим
Задача 2:
В лесу растет миллион елок. Известно, что на каждой из них не более 600000 иголок. Докажите, что в лесу найдутся две елки с одинаковым числом иголок.
Решение:
Перед нами миллион «кроликов»-елок и, увы, всего лишь 600001 клетка с номерами от 0 до 600000. Каждый «кролик»-елка сажается нами в клетку с номером, равным количеству иголок на этой елке. Так как «кроликов» гораздо больше, чем клеток, то в какой-то клетке сидит по крайней мере два «кролика» – если бы в каждой сидело не более одного, то всего «кроликов»-елок было бы не более 600001 штук. Но ведь, если два «кролика»-елки сидят в одной клетке, то количество иголок у них одинаково.
Задача 3:
Дано 12 целых чисел. Докажите, что из них можно выбрать два, разность которых делится на 11.
Решение:
Остатки по модулю 11 – «клетки», числа – «кролики».
Задача 4:
В городе Ленинграде живет более 5 миллионов человек. Докажите, что у каких-то двух из них одинаковое число волос на голове, если известно, что у любого человека на голове менее миллиона волос.
Решение:
Постройте миллион клеток с номерами от 0 до 999999 и рассадите там людей, поместив каждого ленинградца в клетку, номер которой равен количеству волос на его голове.
Задача 5:
В магазин привезли 25 ящиков с тремя разными сортами яблок (в каждом ящике яблоки только одного сорта). Докажите, что среди них есть по крайней мере 9 ящиков с яблоками одного и того же сорта.
Решение:
25 ящиков-«кроликов» рассадим по 3 клеткам-сортам. Так как 25 = 3 8 + 1, то применим «обобщенный принцип Дирихле» для N = 3, k = 8 и получим, что в какой-то клетке-сорте не менее 9 ящиков.
Задача 6:
В стране Курляндии m футбольных команд (по 11 футболистов в каждой). Все футболисты собрались в аэропорту для поездки в другую страну на ответственный матч. Самолет сделал 10 рейсов, перевозя каждый раз по m пассажиров. Еще один футболист прилетел к месту предстоящего матча на вертолете. Докажите, что хотя бы одна команда была целиком доставлена в другую страну.
Решение:
Так как перевезено всего 10m + 1 футболистов, то, рассадив их по клеткам-командам, получаем, что в какой-то клетке сидит 11 футболистов.
Задача 7:
Дано 8 различных натуральных чисел, не больших 15. Докажите, что среди их положительных попарных разностей есть три одинаковых.
Решение:
Различных разностей может быть 14 – от 1 до 14 – это те 14 клеток, в которые мы будем сажать кроликов. Кто же будет нашими кроликами? Ими, конечно, должны быть разности между парами данных нам натуральных чисел. Однако имеется 28 пар и их можно рассадить по 14 клеткам так, что в каждой клетке будет сидеть ровно два «кролика» (и значит, в каждой меньше трех). Здесь надо использовать дополнительное соображение: в клетке с номером 14 может сидеть не более одного кролика, ведь число 14 можно записать как разность двух натуральных чисел, не превосходящих 15, лишь одним способом: 14 = 15 – 1. Значит, в оставшихся 13 клетках сидят не менее 27 кроликов, и применение обобщенного принципа Дирихле дает нам желаемый результат.
Задача 8:
Докажите, что в любой компании из 5 человек есть двое, имеющие одинаковое число знакомых в этой компании.
Решение:
Вариантов числа знакомых всего 5: от 0 до 4. Осталось заметить, что если у кого-то 4 знакомых, то ни у кого не может быть 0 знакомых.
Задача 9:
Несколько футбольных команд проводят турнир в один круг. Докажите, что в любой момент турнира найдутся две команды, сыгравшие к этому моменту одинаковое число матчей.
Решение:
Пусть всего команд n. Тогда вариантов числа команд, с которыми сыграла данная команда n: от 0 до n – 1. Осталось заметить, что если одна команда сыграла со всеми n – 1-й, то никакая другая команда не могла ни с кем не сыграть.
Задача 10:
а) Какое наибольшее число полей на доске 8 × 8 можно закрасить в черный цвет так, чтобы в любом уголке вида из трех полей было по крайней мере одно незакрашенное поле?
б) Какое наименьшее число полей на доске 8 × 8 можно закрасить в черный цвет так, чтобы в каждом уголке вида было по крайней мере одно черное поле?
Решение:
а) Разбейте доску на 16 квадратиков 2 × 2 – это клетки; кроликами, конечно, будут черные поля.
Задача 11:
10 школьников на олимпиаде решили 35 задач, причем известно, что среди них есть школьники, решившие ровно одну задачу, школьники, решившие ровно две задачи и школьники, решившие ровно три задачи. Докажите, что есть школьник, решивший не менее пяти задач.
Решение:
Из условий следует, что найдутся 7 школьников, решивших 35 – 6 = 29 задач. Так как 29 = 4 7 + 1, то найдется школьник, решивший не менее пяти задач.
Задача 12:
Какое наибольшее число королей можно поставить на шахматной доске так, чтобы никакие два из них не били друг друга?
Решение:
Ответ: 16 королей. Разобьём доску на 16 квадратиков, в каждом может быть не более одного короля.
Задача 14:
Докажите, что равносторонний треугольник нельзя покрыть двумя меньшими равносторонними треугольниками.
Решение:
Каждый из меньших треугольников не может накрывать более одной вершины большого треугольника.
Задача 15:
В квадрат со стороной 1 метр бросили 51 точку. Докажите, что какие-то три из них можно накрыть квадратом со стороной 20 см.
Решение:
Разобьем наш квадрат на 25 квадратов со стороной 20 см. По обобщенному принципу Дирихле, в какой-то из них попадет по крайней мере три точки из 51 брошенной.
Задача 16:
Пятеро молодых рабочих получили на всех зарплату – 1500 рублей. Каждый из них хочет купить себе магнитофон ценой 320 рублей. Докажите, что кому-то из них придется подождать с покупкой до следующей зарплаты.
Решение:
Если бы каждый из рабочих мог купить магнитофон, то у них в сумме было бы не менее 5 320 = 1600 рублей.
Задача 17:
В бригаде 7 человек и их суммарный возраст – 332 года. Докажите, что из них можно выбрать трех человек, сумма возрастов которых не меньше 142 лет.
Решение:
Покрасим всю сушу в синий цвет, а все точки, диаметрально противоположные суше – в красный. Тогда обязательно есть точка, которая покрашена в оба цвета. В ней и надо рыть туннель.
Задача 19:
Докажите, что среди степеней двойки есть две, разность которых делится на 1987.
Решение:
Рассмотрите 1988 степеней и их остатки по модулю 1987.
Задача 20:
Докажите, что из 52 целых чисел всегда найдутся два, разность квадратов которых делится на 100.
Решение:
Квадраты при делении на 100 могут давать лишь 51 остаток, так как остатки x и 100 – x при возведении в квадрат дают один и тот же остаток.
Задача 21:
Докажите, что среди чисел, записываемых только единицами, есть число, которое делится на 1987.
Решение:
Рассмотрим 1988 чисел-«кроликов» 1, 11, 111, …, 111 … 11 (1988 единиц) и посадим их в 1987 клеток с номерами 0, 1, 2, …, 1986 – каждое число попадает в клетку с номером, равным остатку от деления этого числа на 1987. Тогда (по принципу Дирихле) найдутся два числа, которые имеют одинаковые остатки при делении на 1987. Пусть это числа 11 … 11 (m единиц) и 11 … 11 (n единиц), причем m > n. Но их разность, которая делится на 1987, равна 11 … 1100 … 00 (m – n единиц и n нулей). Сократим все нули – ведь они не имеют никакого отношения к делимости на 1987 – и получим число из одних единиц, которое делится на 1987.
Задача 22:
Докажите, что существует степень тройки, оканчивающаяся на 001.
Решение:
Если 3 m и 3 n – степени тройки, дающие один и тот же остаток при делении на 1000, то 3 m – 3 n = 3 n (3 m – n – 1) делится на 1000 (мы считаем для определенности, что m > n).
Задача 23:
В клетках таблицы 3 × 3 расставлены числа – 1, 0, 1. Докажите, что какие-то две из 8 сумм по всем строкам, всем столбцам и двум главным диагоналям будут равны.
Решение:
Эти суммы могут принимать лишь 7 разных значений: от – 3 до 3.
Задача 24:
Сто человек сидят за круглым столом, причем более половины из них – мужчины. Докажите, что какие-то два мужчины сидят друг напротив друга.
Решение:
Разобьем всех людей на 50 пар так, что в каждой паре – два человека, сидящих друг напротив друга. Ясно, что в одной из этих пар-«клеток» оба человека – мужчины.
Задача 25:
15 мальчиков собрали 100 орехов. Докажите, что какие-то два из них собрали одинаковое число орехов.
Решение:
Если это не так, то, очевидно, что мальчики собрали не менее, чем 0 + 1 + 2 + … + 14 = 105 орехов – противоречие.
Задача 26:
Цифры 1, 2, …, 9 разбили на три группы. Докажите, что произведение чисел в одной из групп не меньше 72.
Решение:
Произведение чисел во всех группах равно 9! = 362880, а 71³ = 357911.
Задача 27:
В таблице 10 × 10 расставлены целые числа, причем любые два числа в соседних клетках отличаются не более, чем на 5. Докажите, что среди этих чисел есть два равных.
Решение:
Поскольку от любой клетки до любой другой можно добраться, не более 19 раз сдвинувшись в соседнюю клетку, то все числа находятся между числами a и a + 95, где a – минимальное из всех расставленных чисел. Значит, среди этих чисел не более 96 различных.
Задача 28:
Докажите, что среди любых 6 человек есть либо трое попарно знакомых, либо трое попарно незнакомых.
Решение:
У данного человека среди остальных пяти есть либо не менее трех знакомых, либо не менее трех незнакомых ему. Разберем, например, первый случай. Среди этих трех людей есть либо двое знакомых – тогда они вместе с выбранным нами исходно человеком образуют нужную тройку, либо они все трое попарно незнакомы.
Задача 29:
На клетчатой плоскости дано 5 произвольных узлов сетки. Докажите, что середина одного из отрезков, соединяющих какие-то две из этих точек, также является узлом сетки.
Решение:
Рассмотрите координаты этих точек и их остатки при делении на 2.
Задача 30:
На складе имеется по 200 сапог 41, 42 и 43 размеров, причем среди этих 600 сапог 300 левых и 300 правых. Докажите, что из них можно составить не менее 100 годных пар обуви.
Решение:
В каждом размере каких-то сапог меньше: правых или левых. Выпишем эти типы сапог по размерам. Какой-то тип, например, левый, повторится по крайней мере дважды, например, в 41 и 42 размерах. Но так как количество левых сапог в этих размерах суммарно не меньше 100 (почему?), то мы имеем не менее 100 годных пар обуви в этих размерах.
Задача 31:
В алфавите языка племени Ни-Бум-Бум 22 согласных и 11 гласных, причем словом в этом языке называется произвольное буквосочетание, в котором нет двух согласных подряд и ни одна буква не использована дважды. Алфавит разбили на 6 непустых групп. Докажите, что из всех букв одной из групп можно составить слово.
Решение:
Докажите, что в одной из групп разность между числом согласных и числом гласных не больше 1.
Задача 32:
Докажите, что среди любых 10 целых чисел найдется несколько, сумма которых делится на 10.
Решение:
Задача 33:
Дано 11 различных натуральных чисел, не больших 20. Докажите, что из них можно выбрать два числа, одно из которых делится на другое.
Решение:
Разбейте числа от 1 до 20 на 10 наборов, в каждом из которых в любой паре чисел одно делится на другое: 11, 13, 15, 17, 19, 1,2,4,8,16, 3,6,12, 5,10,20, 7,14, 9,18.
Задача 34:
11 пионеров занимаются в пяти кружках дома культуры. Докажите, что найдутся два пионера А и В такие, что все кружки, которые посещает А, посещает и В.
Решение:
Занумеруем кружки числами от 1 до 5 и вместо каждого пионера будем рассматривать тот набор кружков – подмножество множества 1,2,3,4,5 – который состоит из посещаемых им кружков. Осталось разбить 32 подмножества указанного множества на 10 наборов так, чтобы в каждом из наборов из любых двух множеств этого набора одно содержалось в другом. В качестве таких наборов рассмотрим следующие: 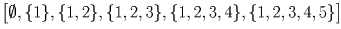
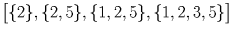
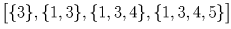
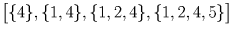
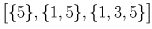
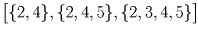
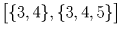
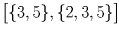
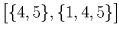
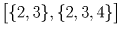
 masterok
masterok
Мастерок.жж.рф
Хочу все знать
Впервые о парадоксе колеса заговорили ещё до Аристотеля, однако он первый вплотную занялся его изучением. Затем над решением этой задачки бился Галилео Галилей. Хотя многим это покажется совершенно очевидным. Но давайте по порядку …
Аристотелево колесо — так называют обыкновенно кажущийся парадокс, представляющийся при движении колеса около оси, когда самое колесо катится на плоскости по прямой линии. Полагают, что Аристотель впервые заметил этот странный парадокс, который по этой причине и удержал наименование «Аристотелева колеса».
Положим, что круг, обращаясь вокруг своего центра, катится в то же время по прямой линии и с совершением полного оборота описывает прямую, коей длина равна окружности круга. Если в этом круге, который назовем главным, вообразим другой, меньший, одноцентренный с первым и движущийся вместе с ним, то по совершении большим кругом полного оборота малый круг опишет прямую линию, равную уже не своей окружности, а окружности главного круга. Пример подобного кажущегося парадокса можно видеть в движении каретного колеса, ступица которого при своем обращении перейдет прямую, большую своей окружности и равную окружности самого колеса. Приведенный пример, как известно, подтверждается ежедневным опытом.
Но тут рождается вопрос, как объяснить, что окружность ступицы описывает прямую, большую этой самой распрямленной окружности?
А если представить, что всё это правда? Тогда технически возможно, что колесо с окружностью в 2,54 сантиметра в состоянии пройти тот же путь за один оборот, что и колесо с окружностью, равной 1,6 километров.
Но такого просто не бывает. Длина окружности с меньшим радиусом не может быть равна длине окружности с большим радиусом. Так в чём же дело?
Решение Аристотелем данного парадокса заключается в ясном и последовательном изложении всех моментов факта, представляющего некоторое затруднение. Галилей, также пытавшийся объяснить приведенный парадокс, вообразил бесчисленное множество бесконечно малых пустот (vuldes infiniment petits), распределенных по двум прямым линиям, описываемым обоими кругами; он утверждал, что малый круг не касается точками своей окружности к пустым пространствам переходимой им прямой линии и, таким образом, описывает только линию, равную длине своей окружности. Нет надобности, кажется, доказывать слишком очевидную неосновательность подобного объяснения. Существуют и другие попытки ученых объяснить явление так называемого Ар. колеса, но все они большею частью неудовлетворительны.
Первое настоящее решение этого парадокса было предложено членом Парижской академии Дорту-де-Мераном (Dortous de Mairan) в 1715 г. Он объяснил кажущееся противоречие приведенного случаяскольжением ступицы колеса по прямой линии, переходимой точками ее окружности.
Можно разрешить затруднение еще и другим образом. Вообразим круг, обращающийся около своего центра в то время, как последний (т. е. центр) движется по прямой линии; очевидно, что прямолинейное движение центра вовсе не зависит от вращательного движения круга, а следовательно, и отношение скоростей, соответствующих обоим движениям, вполне произвольно. Очевидно, что легко уподобить катящееся на плоскости колесо с кругом, обращающимся около своего центра, между тем как этот центр движется параллельно упомянутой плоскости. Следовательно, так же легко вообразить движение колеса, как и движение круга.
Давайте проследим маршрут, который проходит каждая точка окружности от начала красной линии до её конца. Перемещайте свой палец по линии, обозначающей радиус круга, одновременно следя за траекторией, которую проходит малая окружность от начала пути до конца.
Затем проследите траекторию, которую проходит большая окружность от начала пути до конца. Очевидно, что точка на большей окружности проходит бо́льшую траекторию, а, следовательно, больший путь, чтобы добраться до той же точки.
Иначе говоря, можно ехать в Москву из Нижнего Новгорода через Владимир, а можно через Архангельск или Астрахань. Расстояние от Нижнего до Москвы остаётся неизменным, но пути, которые придётся проделать по этим маршрутам, далеко не одинаковы.
Можно это объяснить еще вот так: этот парадокс возник из-за непонимания разницы между словами «путь» и «перемещение». Перемещение будет одинаково в любом случае ( если вы переместите камень на километр при любом радиусе любая его точка переместится на километр) а вот путь они проходят разный, путь это то расстояние которое прошли точки пересечения линии, которая отсекает полный оборот, с окружностями и он разный)
В этом-то и заключается объяснение парадокса, над которым ломали голову самые выдающиеся умы человечества.
Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона. — С.-Пб.: Брокгауз-Ефрон. 1890—1907.
Калейдоскопы
В мае 2020 года ушел из жизни выдающийся математик, профессор Московского государственного университета имени М. В. Ломоносова и Независимого Московского университета Э. Б. Винберг. Эрнест Борисович — автор большого числа книг и учебников для студентов и школьников, многие годы он был главным редактором сборника «Математическое просвещение».
В предисловии к своему замечательному учебнику «Курс алгебры» Э. Б. Винберг пишет: «В соответствии со своим взглядом на математику я стремился заменить выкладки и сложные рассуждения идеями. Кому-то это может показаться трудным, но усилия, потраченные на освоение идей, окупятся возможностью самостоятельно решать задачи, не рассматриваемые в учебнике». Эрнест Борисович придерживался этого принципа на протяжении всех лет занятий математикой и преподавания. Это одна из причин, по которой работы Винберга написаны столь ясно, а лекции и выступления на семинарах так хорошо структурированы и увлекательны.
Предлагаем вашему вниманию статью Э. Б. Винберга, опубликованную в «Соросовском образовательном журнале» (1997, №2)
Калейдоскоп (что в переводе с греческого означает ‘смотрю красивый вид’) — это детская игрушка, в которой разноцветные кусочки стекла, многократно отражаясь в трех зеркалах, создают красивый узор. Зеркала эти расположены как боковые грани правильной треугольной призмы, образуя между собой углы, равные π/3. Если бы эти углы были другими, то отражения накладывались бы друг на друга и не создавали симметричного узора. Однако имеются исключительные случаи, когда этого не происходит. Все они могут быть легко найдены, что и будет сделано в разделе 2.
Описанный выше обычный калейдоскоп по существу двумерен, так как мы видим в нем плоский узор. Можно представить себе трехмерный калейдоскоп как многогранную камеру с зеркальными стенками. Наблюдатель, помещенный в нее, увидит многократные отражения всех находящихся в ней предметов. Как правило, эти отражения будут перекрываться, но есть несколько случаев (мы их опишем в разделе 4), когда отражения не перекрываются и создают симметричный трехмерный узор.
Если отбросить в сторону возможность практической реализации, то можно говорить и о многомерных калейдоскопах, а также о неевклидовых калейдоскопах, а именно о калейдоскопах на сфере и в пространстве Лобачевского. Калейдоскопы в евклидовом пространстве и на сфере любой размерности были исчерпывающим образом описаны английским математиком Г. С. М. Кокстером в 1934 году. На обложке его переведенной на русский язык популярной книги [1] изображен один из калейдоскопов на обычной (двумерной) сфере (см. рис. 4). Сферические калейдоскопы тесно связаны с правильными многогранниками (см. раздел 3).
Калейдоскопы на плоскости Лобачевского использовались еще в конце прошлого века А. Пуанкаре и Ф. Клейном в их исследованиях по теории автоморфных функций комплексного переменного. В 1958–1960 годах голландский художник М. К. Эшер создал несколько оригинальных картин-узоров на базе этих калейдоскопов (таких, как на рисунке 5).
Калейдоскопы в пространстве Лобачевского стали объектом интенсивных исследований начиная с 1965 года в связи с некоторыми проблемами теории групп. Их полное описание в любой размерности еще далеко от завершения. Имеется удивительный результат (принадлежащий автору статьи) о том, что при n ≥ 30 в n-мерном пространстве Лобачевского вообще не существует калейдоскопов. Примеры таких калейдоскопов известны лишь при n ≤ 8.
Помимо уже упоминавшихся приложений калейдоскопов в геометрии (правильные многогранники), теории функций комплексного переменного и теории групп имеются не менее важные их приложения в теории чисел, теории алгебр Ли, алгебраической геометрии и других разделах математики. Следует, впрочем, сказать, что в серьезной математической литературе термин «калейдоскоп» не употребляется. Вместо этого говорят «дискретная группа, порожденная отражениями».
В статье мы не имеем возможности говорить о приложениях калейдоскопов (за исключением связи сферических калейдоскопов с правильными многогранниками). Однако изучение калейдоскопов самих по себе составляет яркую страницу геометрии. Более полные сведения о калейдоскопах можно найти в обзорной статье [2].
1. Основное свойство калейдоскопов
Рассмотрим простейшую ситуацию — два зеркала, расположенные под некоторым углом α одно к другому. Если угол α не является целой частью π, то, как показано на рисунке 1, а, изображения предмета, помещенного между зеркалами, будут перекрываться, так что в одной точке мы будем видеть изображения двух разных точек. (На самом деле мы сможем увидеть в одной точке изображения двух разных точек не одновременно, а только перемещая точку зрения, но это не имеет отношения к нашему теоретическому обсуждению.) Если же угол α является целой частью π, как, например, на рисунке 1, б, то этого не происходит.
Рис. 1. Система из двух зеркал
Так как изображения каждой точки не выходят за пределы плоскости, перпендикулярной общей оси наших зеркал (именно такая плоскость и изображена на рисунке 1), то обнаруженное нами явление по существу двумерно. Можно говорить о зеркальном отражении плоских фигур относительно прямых, и рисунок 1 демонстрирует, что изображения, полученные многократными отражениями относительно сторон угла, не перекрываются тогда и только тогда, когда величина α этого угла является целой частью π. Более точно, если α = π/k, где k ≥ 2 — натуральное число, то вся плоскость оказывается разбитой на 2k равных углов с общей вершиной, в каждом из которых получается одно изображение внутренности исходного угла. В половине из этих углов изображения являются зеркально обращенными, в другой половине, включающей сам исходный угол, — необращенными.
Представим себе теперь выпуклый многоугольник, образованный зеркалами. В каком случае изображения, получаемые многократными отражениями внутренности многоугольника относительно его сторон, не будут перекрываться? Из предыдущего следует, что для этого необходимо, чтобы все углы многоугольника были целыми частями π. Можно показать, что это условие является и достаточным. Если оно выполнено, то вся плоскость оказывается разбитой на многоугольники, равные исходному, таким образом, что любые два многоугольника, имеющие общую сторону, симметричны относительно этой стороны. В каждом из многоугольников этого разбиения получается одно изображение внутренности исходного многоугольника. На рисунке 2 показано разбиение плоскости, получаемое из равностороннего треугольника. Именно это разбиение мы видим, глядя в обычный калейдоскоп.
Рис. 2. Обычный калейдоскоп
Точно так же изображения, получаемые многократными отражениями внутренности выпуклого многогранника относительно его граней, не перекрываются тогда и только тогда, когда все двугранные углы многогранника являются целыми частями π. Эта теорема справедлива и для неевклидовых многоугольников и многогранников.
Многоугольник (многогранник), все (двугранные) углы которого являются целыми частями π, называется многоугольником (многогранником) Кокстера. Таким образом, описание теоретически возможных калейдоскопов равносильно описанию многоугольников и многогранников Кокстера.
2. Двумерные калейдоскопы
Нетрудно найти все многоугольники Кокстера на евклидовой плоскости. Как известно, сумма углов евклидова n-угольника равна π(n − 2), так что среднее арифметическое его углов равно π(1 − 2/n), что при n = 4 составляет π/2. Но все углы многоугольника Кокстера, как явствует из определения, не больше π/2. Поэтому единственным четырехугольником Кокстера является прямоугольник, а многоугольников Кокстера с большим числом сторон вообще не существует.
Далее, так как сумма углов треугольника равна π, то для треугольника Кокстера с углами π/k, π/l, π/m мы получаем диофантово уравнение
С точностью до перестановки чисел k, l, m оно имеет три решения:
Таким образом, имеется ровно три треугольника Кокстера: равносторонний, равнобедренный прямоугольный и прямоугольный с острыми углами π/3 и π/6. Соответствующие разбиения плоскости изображены на рисунке 3. Вместе с прямоугольником это дает четыре типа двумерных евклидовых калейдоскопов.
Рис. 3. Двумерные евклидовы калейдоскопы
Аналогичным образом можно найти все двумерные сферические калейдоскопы. Сумма углов сферического n-угольника больше π(n − 2) (простое доказательство этого см., например, в [3]). Поэтому в отношении сферических многоугольников Кокстера наши выводы о числе сторон только усугубляются, а именно, не существует сферических многоугольников Кокстера, отличных от треугольника. Для сферического треугольника Кокстера уравнение (1) заменяется на неравенство
имеющее следующие решения:
(2, 2, m), (2, 3, 3), (2, 3, 4), (2, 3, 5).
Рис. 4. Сферический калейдоскоп
Первому из этих решений отвечает разбиение сферы на 4m «бипрямоугольных» треугольников, осуществляемое экватором и 2m равноотстоящими друг от друга меридианами. Решению (2, 3, 5) отвечает разбиение, изображенное на рисунке 4. В разделе 3 мы еще вернемся к сферическим калейдоскопам в связи с правильными многогранниками.
3. Сферические калейдоскопы и правильные многогранники
Рис. 6. Фундаментальный конус куба
С каждым правильным многогранником можно связать сферический калейдоскоп. Пусть М — правильный многогранник с центром в точке О. Пусть А — центр какой либо его грани, В — середина какой-либо стороны этой грани и С — какая-либо из двух вершин, принадлежащих этой стороне. Трехгранный конус K с вершиной в точке О, ребра которого проходят через точки А, В, С соответственно, назовем фундаментальным конусом многогранника М (на рисунке 6 в качестве М взят куб).
За счет различного выбора грани, ее стороны и вершины, принадлежащей этой стороне, можно построить много разных фундаментальных конусов данного многогранника. Они не перекрываются и в совокупности покрывают все пространство. Их число N может быть подсчитано по любой из следующих формул:
где приняты следующие обозначения: Г — число граней многогранника М, Р — число его ребер, В — число его вершин, р — число сторон (каждой) грани, q — число ребер, выходящих из (каждой) вершины. Так, в случае куба
Г = 6, Р = 12, В = 8, р = 4, q = 3, N = 48.
Плоскость любой грани фундаментального конуса является плоскостью симметрии многогранника М, и любые два фундаментальных конуса, имеющие общую грань, симметричны относительно плоскости этой грани. Например, в случае куба плоскость ОАС есть плоскость симметрии, проходящая через два противоположных ребра; конус K′, симметричный конусу K относительно этой плоскости, есть фундаментальный конус, ребра которого проходят через точки А, С, B′ (см. рис. 6).
Ребро OA конуса K является общим ребром 2р фундаментальных конусов, имеющих при этом ребре один и тот же двугранный угол. Следовательно, двугранный угол конуса K при ребре OA равен π/p. Аналогично устанавливается, что двугранный угол при ребре ОВ равен π/2, а при ребре ОС равен π/q. Отсюда мы заключаем, что пересечение любого фундаментального конуса со сферой, концентрической многограннику М, есть прямоугольный сферический треугольник с острыми углами π/p и π/q. Любые два из этих треугольников, имеющие общую сторону, симметричны относительно нее. Тем самым мы получили сферический калейдоскоп.
При переходе от правильного многогранника к сферическому калейдоскопу теряется информация о том, какое из ребер OA и ОС фундаментального конуса проходило через центр грани, а какое — через вершину многогранника М. Если мы рассмотрим правильный многогранник M′, вершинами которого служат центры граней многогранника М, то ему будет соответствовать тот же сферический калейдоскоп. Такие правильные многогранники М и M′ называют двойственными друг другу. Так, например, куб двойствен октаэдру. Тетраэдр двойствен сам себе (точнее, правильному многограннику, который также является тетраэдром). При переходе от М к M′ числа p и q, а также Г и В меняются ролями.
Каждому из сферических калейдоскопов, определяемых решениями
неравенства (2), отвечает пара двойственных правильных многогранников. Эти пары суть <тетраэдр, тетраэдр>, <куб, октаэдр>, <додекаэдр, икосаэдр>соответственно. Решению (2, 2, m) не отвечает никакой правильный многогранник, так как по смыслу должно быть р, q ≥ 3.
Известно, что площадь сферического треугольника 1 равна его угловому избытку, т.е. сумме его углов минус π. В частности, площадь прямоугольного сферического треугольника с острыми углами π/p и π/q равна (1/p + 1/q − 1/2)π. Так как площадь всей сферы равна 4π, то отсюда получается еще одна формула для числа N (cp. (4)):
Аналогичная связь существует между n-мерными правильными многогранниками и калейдоскопами на (n − 1)-мерной сфере. Интересно, что, в то время как в трехмерном пространстве существует пять правильных многогранников, в четырехмерном пространстве их шесть, а в n-мерном при n > 4 всего три (аналоги тетраэдра, куба и октаэдра).
4. Трехмерные калейдоскопы
Нахождение многогранников Кокстера затрудняется тем, что соотношения между двугранными углами многогранника не столь просты, как соотношение между углами многоугольника. При пересечении выпуклого многогранника М с маленькой сферой с центром в какой-либо его вершине С образуется выпуклый сферический многоугольник, углы которого равны двугранным углам многогранника М при соответствующих ребрах. Поэтому если, скажем, из вершины С выходит q ребер, то сумма двугранных углов при этих ребрах больше π(q − 2). Отсюда следует, что если все двугранные углы многогранника М не превосходят π/2 (например, если он является многогранником Кокстера), то из каждой его вершины выходят только три ребра. Многогранники, обладающие этим последним свойством, называются простыми. Так, тетраэдр и куб являются простыми многогранниками, а октаэдр — нет.
Этими простыми неравенствами, однако, не исчерпываются соотношения между двугранными углами выпуклого многогранника. Рассмотрим простейший случай, когда М — треугольная пирамида. Занумеруем как-либо ее грани и обозначим через αij = αji угол между i-й и j-й гранями. Средствами линейной алгебры легко доказывается, что двугранные углы евклидовой треугольной пирамиды связаны соотношением
Заметим, что точно так же доказывается, что углы α, β, γ евклидова треугольника связаны соотношением
однако это соотношение при условии, что сумма любых двух из углов α, β, γ меньше π, оказывается равносильным тому, что α + β + γ = π. (Попробуйте это доказать!) Что касается соотношения (6), то оно, к сожалению, не приводится к такому простому виду.
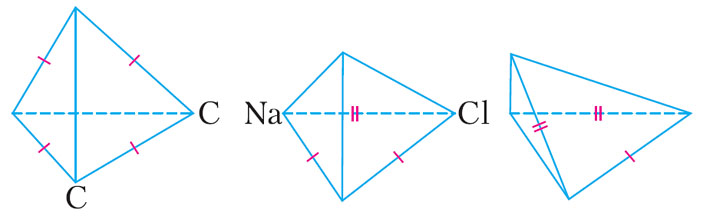
Соотношение (6) вместе с выведенными перед этим неравенствами является необходимым и достаточным условием для того, чтобы в евклидовом пространстве существовала треугольная пирамида с двугранными углами αij. Пользуясь этим, можно найти все евклидовы треугольные пирамиды, двугранные углы которых являются целыми частями π. Их оказывается три. Они изображены на рисунке 7, где принято следующее соглашение: двугранные углы при непомеченных ребрах равны π/2, а при ребрах, перечеркнутых одной или двумя чертами, π/3 или π/4 соответственно. Нетрудно заметить, что первая из пирамид, изображенных на рисунке 7, плоскостью симметрии разрезается на две пирамиды, подобные второй, и так же третья пирамида получается из второй.
Рис. 7. Евклидовы треугольные пирамиды Кокстера
Кроме этих трех калейдоскопов в трехмерном евклидовом пространстве имеется еще только четыре калейдоскопа, которые в определенном смысле сводятся к двумерным. Это прямые призмы, в основании которых лежит двумерный калейдоскоп.
Трехмерные евклидовы калейдоскопы имеют непосредственное отношение к кристаллографии. Некоторые кристаллические решетки могут быть получены, если поместить определенным образом в такой калейдоскоп несколько атомов и рассмотреть все их изображения, получаемые многократными отражениями относительно стенок калейдоскопа. Так, кристаллическая решетка алмаза получается с помощью первого из калейдоскопов, изображенных на рисунке 7, если поместить в двух его вершинах, указанных на рисунке, атомы углерода С, а кристаллическая решетка поваренной соли получается с помощью второго калейдоскопа, если поместить в указанных на рисунке вершинах атомы натрия Na и хлора Cl.
Нетрудно также найти все калейдоскопы на трехмерной сфере. Все они представляют собой (сферические) треугольные пирамиды. Знак равенства в (6) заменяется в этом случае знаком «больше», подобно тому как при переходе от евклидовой плоскости к сфере сумма углов треугольника становится больше π.
5. Теорема Андреева
В пространстве Лобачевского знак равенства в (6) заменяется на знак «меньше». Нетрудно найти все многогранники Кокстера в пространстве Лобачевского, являющиеся треугольными пирамидами. Однако в этом случае они составляют лишь ничтожную часть всех многогранников Кокстера. Подобно тому как на плоскости Лобачевского существуют многоугольники Кокстера со сколь угодно большим (на самом деле любым) числом сторон, в пространстве Лобачевского существуют многогранники Кокстера со сколь угодно большим числом граней. Но в отличие от многоугольников они могут иметь весьма сложное комбинаторное строение. Поэтому получить их полное описание непросто.
В той степени, в какой это вообще представляется возможным, это было сделано Е. М. Андреевым в 1970 году. Он доказал общую теорему, относящуюся не только к многогранникам Кокстера, но и ко всем выпуклым многогранникам, двугранные углы которых не превосходят π/2. Такие многогранники называются остроугольными (хотя они могут иметь и прямые двугранные углы). Как мы доказали в разделе 4 (доказательство не изменяется в случае пространства Лобачевского), всякий остроугольный многогранник является простым.
Теорема Андреева дает необходимые и достаточные условия существования в пространстве Лобачевского остроугольного многогранника заданного комбинаторного строения, отличного от треугольной пирамиды, с заданными двугранными углами. Эти условия суть следующие:
Теорема Андреева в некотором смысле аналогична знаменитой теореме А. Д. Александрова о существовании евклидова многогранника с данной разверткой. Однако ее точного аналога в евклидовой геометрии нет (и не может быть). Это одна из специфических теорем геометрии Лобачевского, подобно признаку равенства треугольников по трем углам.
С помощью теоремы Андреева нетрудно, например, доказать существование в пространстве Лобачевского «прямоугольных» многогранников (т.е. многогранников, все двугранные углы которых прямые) со сколь угодно большим числом граней. (Читатель вполне может сделать это самостоятельно.) Тем самым получим много разнообразных прямоугольных калейдоскопов в пространстве Лобачевского. Не имея возможности обсуждать это подробнее, заметим только, что начиная с конца прошлого века калейдоскопы в пространстве Лобачевского применялись к арифметике квадратичных форм, а в последние 15 лет они получили применение в трехмерной топологии.
Литература
1. Г. С. М. Кокстер. Введение в геометрию. М.: Наука, 1966.
2. Э. Б. Винберг, О. В. Шварцман. Дискретные группы движений пространств постоянной кривизны // Итоги науки и техники. Современные проблемы математики. Фундаментальные направления. М.: ВИНИТИ, 1988, т. 29.
3. Э. Б. Винберг. О неевклидовой геометрии // Соросовский образовательный журнал, 1996, № 3.
1 На сфере единичного радиуса. (Прим. ред.)
2 Матрица Грама семейства векторов образована их попарными скалярными произведениями. Если векторы линейно зависимы, то определитель матрицы Грама равен нулю. Подробнее о матрицах и определителях см., например, в учебнике Э. Б. Винберга «Курс алгебры» (М.: Факториал Пресс, 2001). (Прим. ред.)
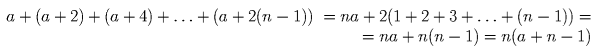
 masterok
masterok