восстановление билинейной формы по квадратичной

Восстановление билинейной формы по квадратичной

Индивидуальные онлайн уроки: Отправьте запрос сейчас: ut2018@protonmail.com
Математика (ЕГЭ, ОГЭ), Английский язык (разговорный, грамматика, TOEFL)
Решение задач: по математике, IT, экономике, психологии Билинейные формы Учебные дисциплины на сайте Bodrenko.org
Портабельные Windows-приложения на сайте Bodrenko.com

Глава 7
БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ

В этой главе изучаются билинейные формы, определенные в вещественном линейном пространстве, т. е. числовые функции двух векторных аргументов, линейные по каждому из этих аргументов. Подробно исследуются так называемые квадратичные формы, представляющие собой билинейные формы, определенные для совпадающих значений их аргументов. Рассматриваются также некоторые приложения теории билинейных и квадратичных форм.

§ 1. Билинейные формы

1. Понятие билинейной формы. Понятие билинейной формы в произвольном линейном пространстве было введено нами ранее в гл.5. Однако для удобства изложения в этом пункте мы напомним некоторые определения и простейшие утверждения.

Определение 1. Числовая функция А(х, у), аргументами которой являются всевозможные векторы х и у вещественного линейного пространства L, называется билинейной формой, если для любых векторов х, у и z из L и любого вещественного числа λ выполняются следующие соотношения:

Иными словами, билинейная форма представляет собой числовую функцию А(х, у) двух векторных аргументов х и у, определенную на всевозможных векторах х и у вещественного линейного пространства L и линейную по каждому из этих аргументов (при этом часто говорят, что билинейная форма А(х, у) задана на линейном пространстве L).
Простейшим примером билинейной формы может служить произведение двух линейных форм f (х) и g(y), определенных на векторах х и у линейного пространства L.
Определение 2. Билинейная форма А(х, у) называется симметричной (кососимметричной), если для любых векторов х и у линейного пространства L выполняются соотношения:

a ξ _i и η _i — координаты в базисе е векторов х и у соответственно.
Доказательство. Пусть — разложение векторов х и у по базису е. Так как форма В(х, у) линейна по каждому из аргументов х и у (см. 7.1)), то

Таким образом, для формы В(х, у) справедливо представление G.3) с выражениями G.4) для коэффициентов b_ij .
Чтобы доказать однозначность этого представления, предположим, что для В(х, у) справедливо представление (7.3) с некоторыми коэффициентами b_ij . Беря в (7.3) х = е_i, у = е_j, мы сразу же получим выражения (7.4) для коэффициентов b_ij. Теорема доказана.
Определение. Матрица

элементы b_ij которой определены с помощью соотношений (7.4), называется матрицей билинейной формы В(х, у) в данном базисе е.
Замечание 1. Обратимся к вопросу о построении всех билинейных форм в данном конечномерном вещественном пространстве L. Ответ на этот вопрос следующий: любая квадратная матрица (b_ij) является в данном базисе е = (е₁, е₂. е _n ) матрицей некоторой билинейной формы.
Убедимся в справедливости этого утверждения.
Определим в линейном пространстве L с данным базисом е = (е₁, е₂. е _n ) с помощью матрицы (b_ij) числовую функцию В(х, у) двух векторных аргументов вида

где С = (c_pq) — матрица перехода от базиса е к базису f, а С ‘ — транспонированная матрица С.
Доказательство. Элементы f_q нового базиса f выражаются через элементы е_р старого базиса е с помощью матрицы С = (c_pq) по формулам

Сумма (по определению произведения матриц) представляет собой элемент матрицы А(е) С. Отсюда следует, что выражение в правой части (7.10) является элементом матрицы С’ А(е) С. Но в левой части (7.10) стоит элемент матрицы A(f). Поэтому A(f) = С ‘ А(е) С. Теорема доказана.
Следствие. Ранг матрицы A(f) равен рангу матрицы А(е).
Это сразу вытекает из соотношения (7.7), из того, что матрица С и, стало быть, матрица С ‘ являются невырожденными, и из теоремы о том, что ранг матрицы не изменяется при умножении ее на невырожденную матрицу.
Это следствие позволяет ввести важный числовой инвариант билинейной формы — так называемый ранг билинейной формы.
Определение 1. Рангом билинейной формы, заданной в конечномерном линейном пространстве L, называется ранг матрицы этой формы в произвольном базисе пространства L.
Определение 2. Билинейная форма А(х, у), заданная в конечномерном линейном пространстве L, называется невырожденной (вырожденной), если ее ранг равен (меньше) размерности пространства L.

Источник

11. Билинейные и квадратичные формы

11.1. Билинейные формы

Определение 11.1. Билинейной формой называется функция (отображение) f: V  V  R (или C), где V – произвольное векторное пространство, и для любых векторов x, y  V и любого числа λ  R (или C) выполняются соотношения

Определение 11.2. Билинейная форма A(x, y) называется симметрической, если для любых x, y  V выполняется: A(x, y) = A(y, x).

Определение 11.3. Билинейная форма A(x, y) называется кососимметрической, если для любых x, y  V выполняется: A(x, y) = –A(y, x).

Свойства билинейных форм

Любую билинейную форму можно представить в виде суммы симметричной кососимметричной форм.

При выбранном базисе e₁, e₂, …, e_n в векторном пространстве V любая билинейная форма A однозначно определяется матрицей

A(е) = ,

A(x, y) = (x₁ x₂ … x_n), то есть

A(x, y) = ,где А_ij = A(e_i, e_j). (1)

Вид (1) назовем общим видом билинейной формы в n-мерном векторном пространстве.

Замечание. Если билинейная форма A(x, y) симметрическая, то и матрица (A_ij) будет симметрической, то есть A_ij = A_ji для i, j = 1, 2, …, n. Если билинейная форма A(x, y) кососимметрическая, то и матрица (A_ij) будет кососимметрической, то есть A_ij = –A_ji для i, j = 1, 2, …, n.

Преобразование матрицы билинейной формы при переходе к новому базису. Ранг билинейной формы

Теорема 11.1. Матрицы A(e) и A(f) билинейной формы A(x, y) в базисах <e> и <f> связаны соотношением

где C – матрица перехода от базиса <e> к базису <f>, а C t –транспонированная матрица C.

Следствие. Ранг матрицы A(f) равен рангу матрицы A(e).

Это утверждение следует из равенства (): так как С – матрица перехода от одного базиса к другому, то матрица С и матрица C t – невырожденные, поэтому умножение на них матрицы A(e) не меняет ее ранга.

Определение 11.5. Билинейная форма называется невырожденной, если ее ранг равен размерности пространства V и вырожденной, если ее ранг меньше размерности пространства V.

11.2. Квадратичные формы

Пусть A(x, y) – симметрическая билинейная форма, заданная на векторном пространстве V.

Определение 11.6. Квадратичной формой называется числовая функция одного векторного аргумента x, которая получается из билинейной формы A(x, y) при x = y.

Определение 11.7. Симметрическая билинейная форма A(x, y) называется полярной квадратичной форме A(x, x).

Пусть дана билинейная форма A(x, y) = , положим в ней x_i = y_j, тогда мы получим представление квадратичной формы A(x, x) в конечномерном векторном пространстве V с заданным базисом <e>:

A(x, x) = . (2)

Определение 11.8. Матрица (a_ij) называется матрицей квадратичной формы A(x, x) в заданном базисе <e>.

При переходе к новому базису матрица квадратичной формы преобразуется по формуле A(f) = C t A(e)C и ранг этой матрицы не меняется при переходе к новому базису.

Определение 11.9. Ранг матрицы квадратичной формы A(x, x) называется рангом квадратичной формы.

Определение 11.10. Квадратичная форма называется невырожденной, если ее ранг равен размерности пространства V и вырожденной, если ее ранг меньше размерности пространства V.

Определение 11.11. Квадратичная форма A(x, x) называется

Положительно определенной, если для любого ненулевого вектора x выполняется неравенство A(x, x) > 0.

Отрицательно определенной, если для любого ненулевого вектора x выполняется неравенство A(x, x) 0 и A(y, y) 0 при х ≠ 0, т. к. A(x, x) положительно определена.

Вывод. Скалярное произведение в векторных пространствах может быть задано с помощью билинейной формы:

(x, y) = = A(x, y).

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник

IX. БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ

Линейные формы

Пусть L_n – n-мерное линейное пространство над полем Р и f –линейное отображение пространства L_nв поле Р (f : L_n® Р).

Легко показать, что множество всех линейных форм f : L_n ® Р является линейным пространством над полем Р.

Билинейные формы

f (а + в, с) = f (а, с) + f (в, с) ; f (а, в + с ) = f (а, в) + f (а, с); f (a×а) = a×f(а).

(Иными словами, билинейная форма линейна по обоим переменным.)

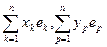
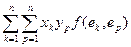
f (а, в) = f ( ) = = , где a_кр – элементы поля Р.

Итак, f (а, в) = (55) – запись билинейной формы в координатах.

Матрица А =

называется матрицей данной билинейной формы. Если х и у – столбцы координат векторов а и в, то билинейную форму можно записать в матричном виде: f (а, в) = х Т × А × у (56)

Определение 60. Билинейная форма называется симметрической, если

f (а, в) = f ( в, а) для любых векторов а и в. (57)

Очевидно, верно следующее утверждение:

Теорема 62. Билинейная форма является симметрической тогда и только тогда, когда она в любом базисе имеет симметрическую матрицу.

Теорема 63. В любом базисе евклидова пространства Е_n скалярное произведение векторов задаётся симметрической билинейной формой.

Доказательство. По формуле (42) скалярное произведение векторов а и в равно

(а, в)= х Т ×Г×у. Матрица Г – симметрическая, поэтому, согласно формуле (56), скалярное произведение задано симметрической билинейной формой.

Квадратичные формы

Пусть L_n – n-мерное линейное пространство над полем Р и пусть на нём задана симметрическая билинейная форма f (а, в).

Определение 61. Симметрическая билинейная форма f (а, в) при условии а = в называется квадратичной формой, заданной на L_n (j(а) = f(а, в) ). При этом f(а, в) и j(а) называются соответствующими друг другу.

j(а) = (59)

Матрица квадратичной формы совпадает с матрицей соответствующей симметрической билинейной формы. Квадратичная форма в матричном виде запишется

j(а) = х Т × А ×х (60)

Если поле Р есть поле рациональных или действительных чисел и

Теорема 64. Всякая квадратичная форма с помощью линейного невырожденного преобразования (преобразования координат) может быть приведена к каноническому виду.

Замечание. Приведение симметрической матрицы к диагональному виду описано в примере пункта 8.3.

Теорема 65.Всякую квадратичную форму линейным невырожденным преобразованием можно привести к нормальному виду.

Доказательство. В теореме 64 доказано, что квадратичную форму можно привести к каноническому виду. Перенумеровав, если нужно переменные, будем считать, что первые r коэффициентов в каноническом виде отличны от нуля, а остальные (n – r) равны нулю.

1) В случае, когда Р = С сделаем преобразование координат по формулам (*).

Пример. Привести к каноническому виду квадратичную форму

Решение. Матрица данной квадратичной формы

Источник

24. Билинейные и квадратичные формы

24.1. Определение билинейной функции. Общие свойства.

Определение. Билинейной функцией f на линейном пространстве L над полем P называется функция от двух векторных аргументов f: L L  P, (x, y)  f(x, y)  P, удовлетворяющая условию линейности по каждому аргументу:

Следствия. Для билинейной функции f выполняются свойства

2.  m, n  N,

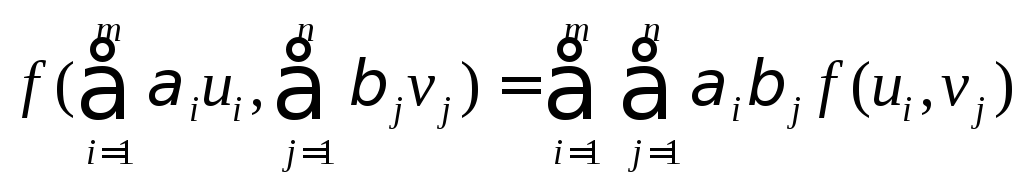
Упражнение. Доказать следствия.

1. Скалярное произведение (x,y) на евклидовом пространстве является билинейной функцей.

Матрица билинейной формы.

любых x, y L имеем где все x_i ,y_j P.

f(x, y) = f . (24.1)

Формула (24.1) показывает, что функция f(x, y) является многочленом от координат х, у, все одночлены которого – первой степени по х и первой степени по у. Такой многочлен называется формой первой степени (то есть линейной) по х, и первой степени (то есть линейной) по у, то есть билинейной формой. Такие билинейные формы мы и будем изучать.

Определим квадратную матрицу = (f_ij ) порядка n, где f_ij = f(e_i, e_j ), i,j = 1,…,n. Матрица называется матрицей билинейной формы f в базисе e.

Из формулы (24.1) f(x, y)== = = = .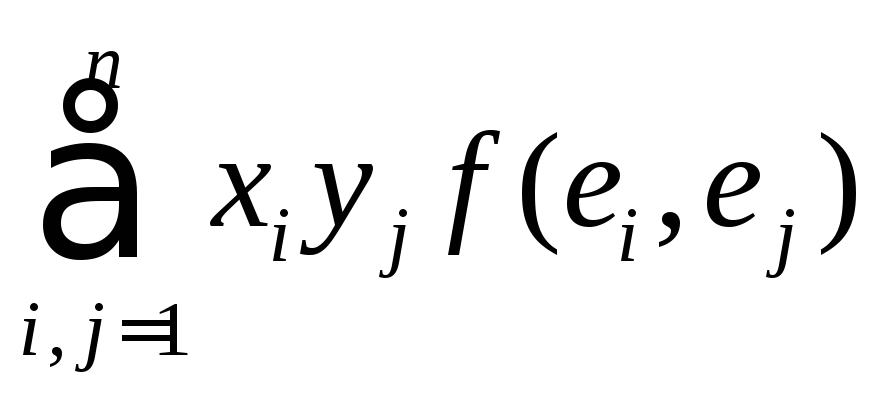

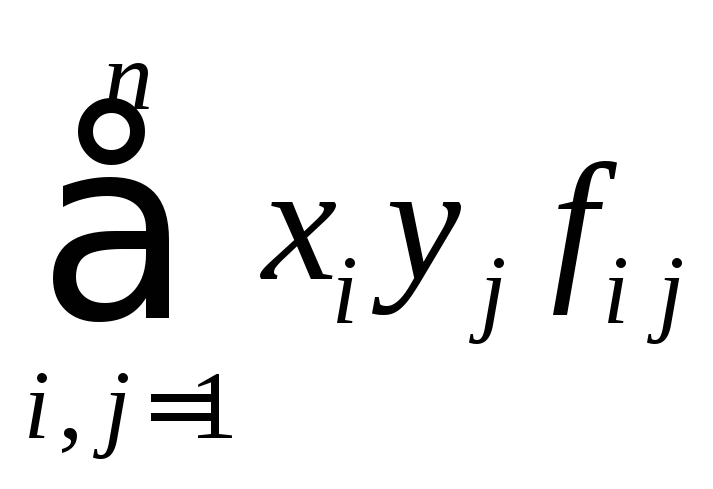
Упражнение. Доказать обратное утверждение: если функция f задается формулой f(x, y)= , то f – билинейная функция, и матрица = (f_ij ).

24.3. Изменение матрицы билинейной формы при изменении базисов. Ранг билинейной формы.

Пусть e = <e₁,…,e_n> – ещё один базис в L, и = T =

. Тогда  x, y L имеем , и

f(x ,y) = ==

= . Следовательно, из единственности матрицы билинейной формы,=.

Следствие. det = det (det T) 2 .

Корректность определения следует из того, что ранг матрицы билинейной формы не зависит от выбора базиса: rg= rg для любых базисов e и e, так как умножение матрицы на невырожденные матрицыT t и T слева и справа соответственно не меняет ранга матрицы билинейной формы.

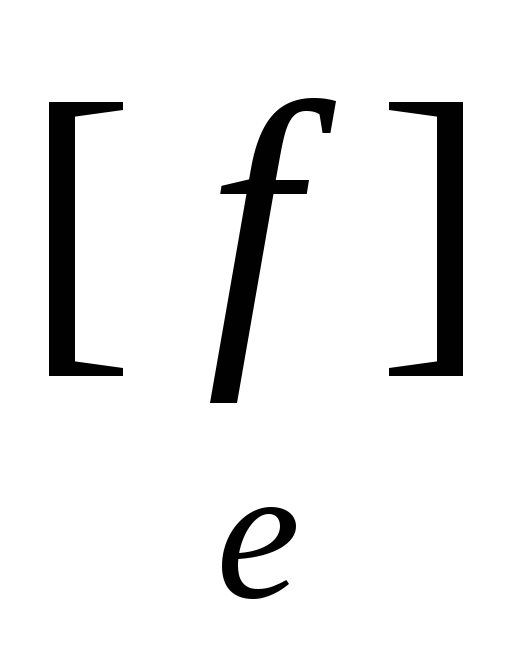
24.4. Определение квадратичной формы. Связь билинейных и квадратичных форм. Матрица и ранг квадратичной формы.

Упражнение. Доказать, что соответствие f  F не инъ-

Утверждение. Если charP  2, то соответствие f  F между симметричными билинейными и квадратичными формами является биекцией.

Следовательно, билинейная форма f однозначно восстанавливается по определенной ею квадратичной форме F, и значит, соответствие f  F является инъекцией.

ная из F по формуле (24.2) будет билинейной.

2. Проверить, что эта форма f будет симметричной, и что

Из упражнений следует, что соответствие f  F является сюръекцией и, следовательно, биекцией.

Определение. Матрицей квадратичной формы F в базисе е называется матрица соответствующей симметричной билинейной формы f : =.

= t . Кроме того, F(x) = ,и по определению rg F = rg f.

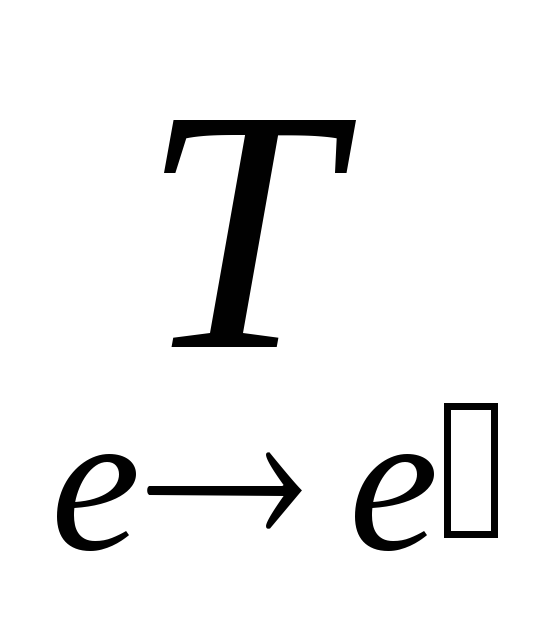
Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник