возникновение счета и чисел
Счет у первобытных людей
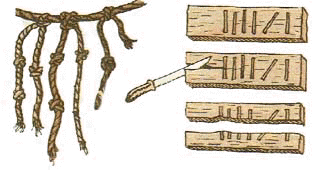
Запоминать большие числа было трудно, и поэтому кроме пальцев рук и ног «задействовались» другие «приспособления». Например, перуанцы использовали для этого разноцветные шнурки с завязанными на них узлами. Веревочные счеты с узелками были в ходу в России, а также во многих странах Европы. До сих пор иногда завязывают узелки на носовых платках на память.
На более высокой стадии развития люди при счете стали применять разные предметы: использовали камешки, зерна, веревку с бирками. Это были первые счетные приборы, которые, в конце концов, привели к образованию разных систем счисления и к созданию современных быстродействующих электронных вычислительных машин.
3. Цифры у разных народов
Мысль выражать все числа знаками
настолько проста, что именно из-за
этой простоты сложно осознать,
сколь она удивительна.
Пьер Симон Лаплас (1749-1827), франц. астроном, математик, физик.
3.1. Появление цифр
Сначала считали на пальцах. Когда пальцы на одной руке кончались, переходили на другую, а если на двух руках не хватало, переходили на ноги. Поэтому, если в те времена кто-то хвалился, что у него «две руки и одна нога кур», это означало, что у него пятнадцать кур, а если это называлось «весь человек», то есть две руки и две ноги.
Перуанские инки вели счет животных и урожая, завязывая узелки на ремешках или шнурках разной длины и цвета. Эти узелки назывались кипу. У некоторых богатеев скапливалось по несколько метров этой веревочной «счетной книги», попробуй, вспомни через год, что означают 4 узелочка на шнурочке! Поэтому того, кто завязывал узелки, называли вспоминателем.
Первыми придумали запись чисел древние шумеры. Они пользовались всего двумя цифрами. Вертикальная чёрточка обозначала одну единицу, а угол из двух лежачих чёрточек – десять. Эти чёрточки у них получались в виде клиньев, потому что они писали острой палочкой на сырых глиняных дощечках, которые потом сушили и обжигали. Вот так выглядели эти дощечки.
Так, например, в древней египетской нумерации, зародившейся более 5000 лет назад, существовали особые знаки (иероглифы) для записи чисел 1, 10, 100, 1000, …
Для того чтобы изобразить, например, целое число 23145, достаточно записать в ряд два иероглифа, изображающие десять тысяч, затем три иероглифа для тысячи, один – для ста, четыре – для десяти и пять иероглифов для единицы
Этого одного примера достаточно, чтобы научиться записывать числа так, как их изображали древние египтяне. Это система очень проста и примитивна.
В начале нашей эры индейцы племени майя, которые жили на полуострове Юкатан в Центральной Америке, пользовались другой системой счисления – двадцатеричной. Они обозначали 1 точкой, а 5 – горизонтальной чертой, например, запись ‗‗‗‗‗‗ означала 14. системе счисления майя был и знак для нуля. По своей форме он напоминал полузакрытый глаз.
В Древней Греции сначала числа 5, 10, 100, 1000, 10000 обозначали буквами Г, Н, Х, М, а число 1 – черточкой /. Из этих знаков составляли обозначения Г (35) и т.д. Позднее числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 200, 300, 400, 500, 600, 700, 800, 900, 1000, 2000, 3000, 4000, 5000, 6000, 7000, 8000, 9000, 10000, 20000 стали обозначать буквами греческого алфавита, к которому пришлось добавить еще три устаревшие буквы. Чтобы отличить цифры от букв, над буквами ставили черточку.
Древние индийцы изобрели для каждой цифры свой знак. Вот как они выглядели.
Они похожи на многие наши цифры. Слово «цифра» тоже досталось нам от арабов по наследству. Арабы нуль, или «пусто», называли «сифра». С тех пор и появилось слово «цифра». Правда, сейчас цифрами называются все десять значков для записи чисел, которыми мы пользуемся: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Постепенное превращение первоначальных цифр в наши современные цифры.
3.2. Римская нумерация
3.3. Цифры русского народа
Арабские числа в России стали применять, в основном, с XVIII века. До того наши предки использовали славянскую нумерацию. Над буквами ставились титлы (черточки), и тогда буквы обозначали числа.
Первые девять чисел записывались так:
Сотни миллионов назывались «колодами».
«
Числа от 11 до 19 обозначались так:
Остальные числа записывались буквами слева направо, например, числа 5044 или 1135 имели соответственно обозначение
При записи чисел больших, чем тысячи, в практической деятельности (счете, торговле и т.д.) часто вместо кружков ставили знаки «; Л» перед буквами, обозначавшими десятки и сотни тысяч, например, запись
означает соответственно 500044 и 540004.
Сколько километров проходит человек за свою жизнь, сколько товаров производится и приходит в негодность ежечасно в пределах города, страны? Сколько времени заняло бы выполнение самым быстрым расчетчиком миллиона вычислительных операций, которые современная вычислительная машина выполняет за. секунду? Во сколько раз скорость пассажирского реактивного самолета превосходит скорость тренированного спортсмена-пешехода? Ответы на эти и тысячи подобных вопросов выражаются числами, занимающими зачастую по числу своих десятичных разрядов целую строку и даже больше.
Для сокращения записи больших чисел давно используется система величин, в которой каждая из последующих в тысячу раз больше предыдущей:
1000 секстиллионов- 1 септиллион
1000 нониллионов- 1 дециллион
Таким образом, 1 дециллион запишется в десятичной системе единицей с 3 х 11=33 нулями:
1 000 000 000 000 000 000 000 000 000 000 000.
Как писал Самуил Яковлевич Маршак: «Напрасно думают, что ноль играет маленькую роль».
При записи больших чисел часто используют степень числа 10.
Заметьте, что число нулей степени 10 всегда равно ее показателю:
10 1 = 10, 10 2 = 100, 10 3 = 1000 и т.д.
И еще одно: математики во всем мире давно приняли, что любое число в нулевой степени равно единице (а 0 = 1).
Числа-символы
0 – абсолют, 1 – его проявление. Все это заключено в Солнце.
2 – двойственность и эмоциональность с ней связанная – свойства Луны.
3 – прошлое, настоящее и будущее время – Сатурн.
4 – четыре стороны света, пространство – Юпитер.
5 – любовь и человек – Венера.
6 – соединение двух треугольников – корень активности, отношений, а также преданность – свойства Марса.
7 – полнота знаний, деталей, особенностей, подвижность – это качества Меркурия.
8 – бесконечность, лунные узлы как точки затмений, во время которых временное соотносится с Вечным.
Возникновение счета и чисел
Введение
На уроке математики мы проходили тему «Натуральные числа», и мне стало интересно:
Как люди научились считать?
Как выглядели первые цифры?
Что знают ученики моего класса о возникновении чисел?
На эти вопросы я попытаюсь ответить в своей работе.
Актуальность темы моего исследования состоит в том, что числа очень важны в нашем мире. Числа сопровождают нашу жизнь повсюду, а задумывались ли мы, что пытаясь подсчитать количество яблок в килограмме, сколько остановок нам ехать до дома, или сколько ступенек до нашего этажа, используем как раз натуральные числа.История возникновения натуральных чисел берет свое начало еще с первобытного общества. Тогда, конечно, оно возникло в самом простейшем виде, но вместе с человечеством развивались и числа. Изначально они использовались только для того, чтобы что-то подсчитать, измерить, т.е. помогали именно в том, что было нужно в практической деятельности людей. Потом число становится частью математики, и история возникновения и развития натуральных чисел обуславливается уже наукой. В самые древние времена люди считали на пальцах, то есть понятия число, в котором мы привыкли его понимать, у них не было. С развитием письменности, развивалось и расширялось понятие числа. Сначала это были черточки, затем были введены другие обозначения, для обозначения больших чисел. До нас дошли вавилонские клинописные таблички с первыми обозначениями натуральных чисел. Сохранившиеся до наших дней «римские цифры» тоже берут свое начало в древности. Огромным прорывом стала индийская позиционная система исчисления, которая позволила записывать числа, используя десять знаков цифр. Греческие философы Пифагор и Архимед тоже внесли свой вклад в историю возникновения чисел. Впервые, в 3 веке до нашей эры, они обосновали понятие бесконечности натурального числа.
Интересно, что ноль появился в системах исчисления гораздо позже, изначально самым маленьким натуральным числом был 1.
Я решил узнать, а что ребята в классе знают о возникновении чисел. Для этого, с разрешения учителя математики, я провёл небольшое анкетирование, которое показало, что 80% одноклассников ничего не знают об истории возникновения натуральных чисел. Я решил сам изучить этот вопрос и с разрешения учителя математики донести изученный материал до одноклассников.
Цель моего исследования – изучение происхождения натуральных чисел и написания цифр.
Задача – узнать историю происхождения натуральных чисел и донести данный материал до одноклассников.
Методы исследования:
Использование информации из Интернет-ресурсов.
Обобщение найденного материала.
Практическая значимость: данный материал можно использовать на уроках математики, как дополнительный материал и во внеклассной работе по предмету.
Интересный факт
Австралийские аборигены племени гумулгал, образ жизни которых примерно такой же, как в неолите, пользовались двоичной системой счисления, то есть у них было всего два слова для чисел: урапон — один, и укасар — два. Все прочие числа образуются из этих двух: урапон- укасар — 3, укасар-укасар — 4, укасар-укасар- урапон — 5 и т. д. Нетрудно заметить, что эта система не очень удобна для обращения с большими числами.
Происхождение чисел
Ученые считают, что история возникновения чисел зародилась еще в доисторические времена, когда человек научился считать предметы. Но знаки для обозначения чисел появились значительно позже: их изобрели шумеры — народ, живший в 3000—2000 гг. до н. з. в Месопотамии (ныне в Ираке). История гласит, что на табличках из глины они выдавливали клинообразные черточки, а потом изобрели знаки. Некоторые клинописные знаки обозначали числа 1, 10, 100, то есть были цифрами, остальные числа записывались посредством соединения этих знаков. Пользование цифрами облегчало счет: считали дни недели, головы скота, размеры земельных участков, объемы урожая.
История цифр началась 5 тысячелетий назад в Египте и Месопотамии. И хотя эти два культурных пласта мало пересекались друг с другом, их системы исчисления очень похожи. Первоначально для записей использовали камень или выполняли засечки на дереве. Впоследствии в Месопотамии стали пользоваться глиняными табличками, а в Египте писали на папирусе. Внешний вид цифр в этих культурах отличается, однако одно можно сказать точно: найденные археологами артефакты подтверждают, что это были не просто записи чисел, а именно математические действия.
Искусство счета развивалось с развитием человечества. В те времена, когда человек лишь собирал в лесу плоды и охотился, ему для счета хватало четырех слов: один, два, три и много. Именно так считают сейчас некоторые племена, живущие в джунглях Южной Америки.
Однако, когда люди начали заниматься животноводством и земледелием, то им уже стало необходимо пересчитывать коз в стаде или количество корзин с выращенными плодами (которых было больше трех), заготовленными на зиму.
Итак, появились числа 1, 2, 3…, которыми можно выразить количество коров в стаде, деревья в саду, волос на голове. Эти числа впоследствии получили название натуральных. Гораздо позднее появился ноль, которым обозначали отсутствие рассматриваемых предметов.
Вавилон нумерация
Знакомясь с числами, мы не можем не заняться знаками, с помощью которых числа обозначаются на бумаге. Знаки эти мы называем цифрами.
Самыми древними цифровыми знаками являются вавилонские знаки. Если мы взглянем на карту, то увидим на ней реки Тигр и Ефрат.
Древние греки назвали эту страну Месопотамией, что по-русски обозначает междуречье, так как расположена она была в долине между двумя реками-близнецами. Часть Месопотамии занимало могучее государство, столицей которого был город Вавилон. Уже четыре тысячелетия назад в Вавилоне расцветала наука и существовали библиотеки. Правда, в те времена еще не было печатных книг, но зато существовали глиняные таблички, на которых вавилонские мудрецы писали свои труды. Современные ученые нашли 44 таблички, на которых записана вся математическая наука, известная вавилонцам. Ученые Вавилона пользовались, так называемой, клинописью. Вавилонские числа являются, собственно говоря, комбинации трех клинописных знаков: единица, десятка и сотни.
С помощью этих знаков можно было написать число тысяча, а также любое другое число, при этом использовались, как принцип сложения, так и умножение, а более крупные числа всегда предшествовали меньшим.
Египетская нумерация
Почти столь же древними являются египетские цифры. Для выражения своих мыслей и слов на бумаге египтяне использовали знаки, которые мы в настоящее время называем иероглифами.
Затем иероглифное письмо было заменено более простым и иератическим письмом. В обоих видах письма египтяне имели специальные знаки для цифр. Египтяне вначале писали числа высшего порядка, а затем низшего. При этом использовался принцип сложения или умножения. Египтяне также умели пользоваться дробями. Все египетские дроби имели в числителе единицу, других дробей они не умели даже выговорить (исключение составляло 2/3). Дроби писали так же, как и натуральные числа, только над ними ставилась точка, причем для 1/2 и для 2/3 имели специальные знаки.
Греческая и римская нумерации
Римляне пользовались дробями со знаменателями 60 (вавилонские) и со знаменателями 12, 24, 48:
1/24 – это половина, а 1/48 – это одна четвертая 1/12.
Римские ученые осваивали дроби в связи со счетом денег и использованием мер и весов. Римская монета Aс, чеканенная первоначально из меди, весила 1 фунт и делилась на 12 унций. Существовало даже специальное название “deunx” для выражения 11/12 (deunx= de uncia), т.е. Ас без одной унции.
Индийская нумерация
Цифры, которыми мы пользуемся в настоящее время, пришли к нам из Индии.
Цифры русского народа
Наши предки пользовались алфавитной нумерацией, то есть числа изображались буквами, над которыми ставится значок – называемый «титло». Чтобы отделить такие буквы – числа от текста, спереди и сзади ставились точки.
Этот способ обозначения цифр называется цифирью. Он был заимствован славянами от средневековых греков – византийцев. Поэтому цифры обозначались только теми буквами, для которых есть соответствия в греческом алфавите.
Для обозначения больших чисел славяне придумали свой оригинальный способ:
десять тысяч – тьма,
десять тем – легион,
десять легионов – леорд,
десять леордов – ворон,
десять воронов – колода.
Такой способ обозначения чисел по сравнению с принятой в Европе десятичной системой был очень неудобен. Поэтому Петр 1 ввел в России привычные для нас десять цифр, отметив буквенную цифирь.
1. Владимир Лёвшин “Магистр рассеянных наук”. Издательский Дом Мещерякова, Москва 2007.
2. Льюис Кэррол “История с узелками”. Издательство “Мир”, Москва 1973.
3. Станислав Коваль “От развлечения к знаниям. Математическая смесь”. WYDAWNICTWA. NAUKOWO-TECHNICZNE WARSZAWA 1972.
4. А.П. Савин, В. В. Станцо, А. Ю. Котова “Я познаю мир. Математика”. “Издательство АСТ-ЛТД”, Москва 1997.
Возникновение счета и чисел
История счётных устройств насчитывает много веков.
Древнейшим счетным инструментом, который сама природа предоставила в распоряжение человека, была его собственная рука. Для облегчения счета люди стали использовать пальцы сначала одной руки, затем обеих, а в некоторых племенах и пальцы ног.
В XVI веке приемы счета на пальцах описывались в учебниках.
Позднее,Около 500 г. н.э., абак был усовершенствован и на свет появились счёты— устройства, состоящего из набора костяшек, нанизанных на стержни.
У японцев это же устройство для счета носило название серобян.
На Руси долгое время считали по косточкам, раскладываемым в кучки. Примерно с XV века получил распространение«дощаный счет», завезенный, видимо, западными купцами вместе с ворванью и текстилем. «Дощаный счет» почти не отличался от обычных счетов и представлял собой рамку с укрепленными горизонтальными веревочками, на которые были нанизаны просверленные сливовые или вишневые косточки.
Приблизительно в 850 году н.э. арабский ученый математик Мухаммед бен Муса ал-Хорезм (из города Хорезма на реке Аму-Дарья) написал книгу об общих правилах решения арифметических задач при помощи уравнений. Она называлась «Китаб ал-Джебр». Эта книга дала имя науке алгебре. Очень большую роль сыграла еще одна книга ал-Хорезми, в которой он подробно описал индийскую арифметику. Триста лет спустя (в 1120 году) эту книгу перевели на латинский язык, и она стала первым учебником «индийской» (то есть нашей современной) арифметики для всех европейских городов.
Мухаммеду бен Муса ал-Хорезму мы обязаны появлению термина «алгоритм«.

В конце XV века Леонардо да Винчи(1452-1519) создал эскиз 13-разрядного суммирующего устройства с десятизубными кольцами. Но рукописи да Винчи обнаружили лишь в 1967г., поэтому биография механических устройств ведется от суммирующей машины Паскаля.По его чертежам в наши дни американская фирма по производству компьютеров в целях рекламы построила работоспособную машину.
История появления чисел
По мнению ученых числа появились еще тогда, когда человеку удалось научиться считать окружающие предметы. Это произошло очень и очень давно. Но знаки, обозначающие числа, появились по меркам истории относительно недавно.
Наука считает, что это произошло в 3000-2000 гг. до н. э. Их изобретение приписывают шумерам – народу, проживавшему на территории Месопотамии (в нынешнее время Ирак).
Историки полагают, что глиняные таблички, на которых они выдавливали определенные черточки, привели к изобретению клинописи. Ею обозначали своеобразные разрядные числа: единицы, десятки, сотни, и также они являлись обозначением цифр. Все остальные записи делались при помощи объединения данных знаков.
Использование цифр существенно упрощало подсчеты: вели счет дням недели, количеству голов скота, объемам урожая, считали размеры участков земли. После шумеров в Месопотамии появились вавилоняне. Они получили систему чисел в наследство от шумеров. До наших дней сохранились таблички-клинопись, на которых изображены превращения шумерских единиц для измерений в вавилонские.
Древние египтяне также использовали цифры. Свидетельством тому является находка Ринда – папирус с математическим трактатом, носящим имя изучавшего Египет англичанина и купившего его в 1858 году в стране пирамид. Такой случай представился в Луксоре. Документ содержит записи 84 математических заданий. Все они с решениями. Глядя на папирус, видно использование в Египте такого порядка цифр, где числовое обозначение – это сумма цифровых значений. При обозначении разрядных чисел, кратных десяти: 1, 10, 100, и т.д., египтяне придумали специальный иероглиф. Записывая разные числа, этот символ использовали такое количество раз, сколько в числе единиц данного разряда.
Похожая система счета существовала у римлян. Ей повезло больше других: она оказалась долгожителем среди древних систем счисления. Иногда ее используют и наши современники.
Такие народы, как финикийцы или древние греки, использовали в качестве цифр буквы.
Историки считают, что появление в Индии первых начертаний знакомых нам цифр произошло в 5 веке. Но индийские обозначения чисел появились в Европе лишь в 10-13 веке. Это сделали путешественники с Ближнего Востока. Поэтому их называют «арабские».
Распространение индийских числовых обозначений в арабских странах приписывают работам двух математиков. Это Хорезми, живший ок. 780-ок. 850 гг. в Средней Азии и арабский ученый Кинди (ок.800-ок. 870). Первый, в Багдаде написал трактат о цифрах из Индии. Европейскую известность труд получил после перевода математика из Италии Леонардо Пизанского (Фибоначчи). Эта работа привела к закреплению арабо-индийской числовой системы в Европе.
Такой подход к написанию чисел предполагает зависимость цифрового значения от местоположения при записи. Например, в числе 151 первая единица – это 100, а последняя – один. По-арабски «ноль» – это сифр, что и преобразовалось в «цифру». Арабское обозначение чисел вошло в обиход в Западной Европе в 15 веке.
Арифметика каменного века
Обучаться счету наши предки стали на заре своего развития. Учила их этому окружающая жизнь. Охота была главным способом добычи еды. Чтобы не упустить жертву, ее окружали с разных сторон. Пять человек с одной стороны, четыре с другой. Здесь счет выходил на первое место. Люди, даже не имея понятий о цифрах, обходились показом на пальцах. До сих пор существуют племена, пользующиеся таким видом счета.
Они используют слово «рука» при счете «пять», 10 – это «две руки». Числительное 20 – это «весь человек», при подсчетах учитываются и пальцы ног.
Число 5 – рука, шестерка – это один палец на второй руке. Десятку составляют две руки или полчеловека. Пятнадцать – плюс пальцы одной ноги, двадцать –полностью человек. А вот 23 – это уже плюс 3 пальца на руке соплеменника. Пересчитывая стадо, состоящее из 128 голов, нужно было 7 человек. Вот так счет начинался с того, чем люди обладали с рождения. Может быть, выражение «Знаю, как свои пять пальцев» означало умение считать вообще, знание того, что на одной руке у человека именно пять пальцев.
Археологи, нашедшие поселение древних людей, обнаружили среди волчьих останков кость, с нанесенными отметинами. 55 нанесенных зазубрин указывают на то, что древний охотник вел расчеты при помощи пальцев. Из рисунка на кости можно узнать, что количество зарубок составляет 11 групп по 5 отметин. Начальные 5 групп отделены от других удлиненной отметиной.
Человечество далеко продвинулось вперед с той поры. Но и поныне швейцарские фермеры, отвозя молоко для обработки, зарубками отмечают количество отправляемых емкостей.
Математика, как наука, начиналась с понятий «меньше», «больше», «столько же». Когда племена производили обмен товарами, можно было обойтись без счета. Просто, рядом с товаром, произведенным одним племенем, раскладывали свой собственный. Этого было достаточно, чтобы произвести обмен между людьми.
Для успешного занятия сельским хозяйством, необходимы были знания арифметики. Не рассчитав количество дней, определить время посева, начало полива составляло определенные трудности. Нужно было определять сроки появления приплода у животных, численность скота в загоне, какое количество урожая помещено в амбары.
Примерно за 6 тыс. лет до н. э. скотоводы того времени начали лепить из глины различные предметы для подсчета животных в стаде. Чтобы узнать, все ли стадо вернулось домой, пастух откладывал в сторону один глиняный кружочек за каждую возвратившуюся овцу. Когда число кружочков и количество животных совпадало, считавший шел отдыхать. Его стадо состояло не только из овец. На пастбища выгоняли коров, коз и других животных. Поэтому возникала потребность в изготовлении и других глиняных фигурок. Люди, обрабатывавшие землю, при помощи таких изделий подсчитывали размеры полученного урожая. Число мешков в амбаре, количество выжатого масла в кувшинах. Сколько у него имеется кусков полотна. Все это требовало подсчета. Когда в стаде случался приплод, хозяин добавлял новые кружочки. При забое скота некоторые фигурки приходилось убирать в сторону.
Так, не зная счета, древние совершали арифметические действия.
Получение названий числами
Постоянное перекладывание фигурок из глины – не самое приятное занятие. Также при больших обменах приходилось вначале пересчитать товары, а затем начинался сам процесс сделки. Но до умения пересчитывать предметы, пролетело немало времени. При этом нужно было найти имена для обозначения количества. «Без названия нет знания» – гласит народная мудрость.
Когда именно числа начали называть определенными именами, историки обнаружили, обратившись к языкам этнических групп и народностей. У нивхов, поселившихся на территории Сахалина и Приамурья, обозначение числительных зависит от вещей, которые пересчитывают. Главную роль при подобных подсчетах играет вид предмета. В языке нивхов при подсчетах «двух яиц», «двух камней», «двух глаз»-числа имеют различные названия. На слово «два» у народности приходятся многие десятки слов. Большое количество несхожих наименований одного и того же числа используют и различные африканские народности, и представители народов, живущих в тихоокеанском регионе.
Прошло немало столетий, или даже тысячелетий, чтобы одинаковые числа стали относиться к различным предметам. В это время и возникли универсальные числовые названия.
Историки думают, что первые названия получили числительные 1 и 2. В радиоэфире и телепрограммах нередко употребляются слова «соло», «солист». Так говорят об одном певце или музыканте. Слово пришло из латинского языка. «Солюс» – один. «Солнце» также походит на «солист». Здесь совсем несложная разгадка. Когда римляне искали название единице, то опирались на свои наблюдения, что Солнце в небе постоянно в одиночестве.
Наименование двойки связывают в различных языковых группах с парными объектами. Это глаза, уши, крылья… Но иногда происходило получение числами 1 и 2 других названий. В этих случаях имена чисел привязывали к местоимениям «я» и «ты». В некоторых языках «один» созвучен «мужчине», «два» повторяет слово «женщина». Числа, после двойки, назывались «много». Позже понадобились и наименования другим числам. Ведь собаки, овцы, стрелы у пастуха или охотника чаще всего были в количестве, большем, чем 2. У небольших народностей не так давно совсем отсутствовали числительных, обозначающих количество предметов, больше двух. И здесь нашелся хороший метод для обозначения чисел. Это повторение названий единиц и двоек.
Позже у некоторых народностей появилось имя у числительного, знакомого нам, как число «три». Это слово применялось для употребления вместо «много», следовавшим за первыми двумя числами.
Сердясь на кого-то, мы произносим: «Я что, три раза должен повторять то же самое!».
В русском фольклоре: «Обещанного три года ждут».
Добры молодцы в сказках ходят за «тридевять земель».
«Четыре» встретить в сказаниях можно не так часто. Но и это числительное имело когда-то свое особое значение. Это видно из правил русского языка. Если вслушаться, то говорится: «одна собака», «две собаки». А начиная с числа 5, говорится: «пять собак», «шесть собак» и так сколько угодно. Хоть миллион, но все равно «собак». Это значит, что во времена наших пращуров, при счете, после числительного «четыре», только начиналось неизведанное. Огромное количество чисел, с таинственным названием «много». И эта область простиралась необозримо далеко.