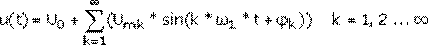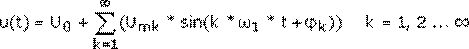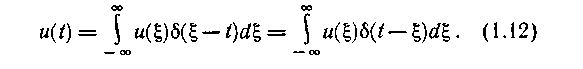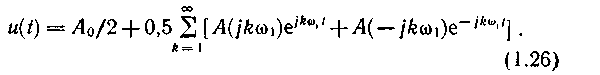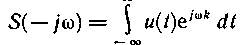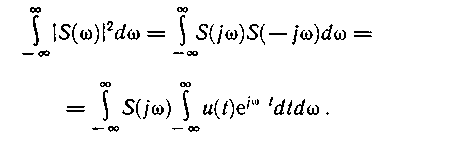временная форма представления сигнала
Временное и спектральное представление сигналов
Страницы работы
Содержание работы
Тема 1.4. Временное и спектральное представление сигналов Раздел I.
Тема 1.4. Временное и спектральное представление сигналов
Формы представления сигналов
Существует две формы представления сигналов:
· временная форма представления сигналов;
· спектральная форма представления сигналов.
Временная форма представления сигнала – это описание изменения его параметров в функции времени. Такая форма описания позволяет определить энергию, мощность и длительность сигнала.
Временная форма может быть представлена:
· математической моделью (аналитической записью);
· временной диаграммой (осциллограммой) сигнала.
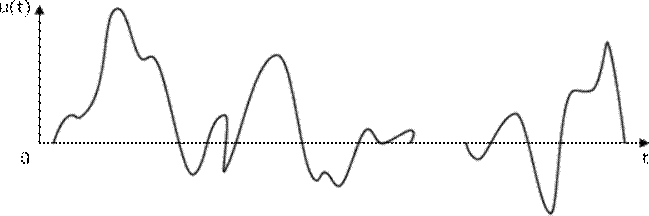
Следует отметить, что выбрать математическую модель для реального электрического сигнала не всегда просто. Для примера рассмотрим телефонный сигнал, реализации различных фрагментов которого приведены на рис. 1.4.1. Даже визуальный анализ этих временных диаграмм приводит к заключению, что совсем непросто подобрать функцию времени, которая точно совпадала бы, например, с временной диаграммой u(t) на всем интервале времени [0,Т]. Если бы такую функцию удалось найти, то, скорее всего, она была бы представлена достаточно сложным выражением. Поэтому можно сказать, что временные диаграммы телефонного сигнала имеют сложную форму.
Практически все электрические сигналы, используемые в электросвязи для представления сообщений, имеют сложную форму. Это утверждение относится, в частности, к сигналам вещания, а также телевизионным, телеграфным сигналам и др.
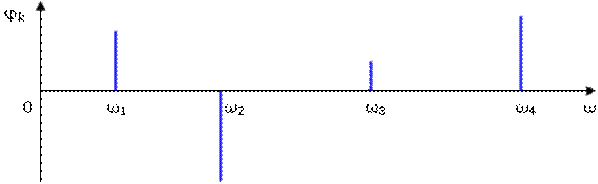
Для исследования частотных свойств сигналов используется спектральное представление функции с помощью преобразования Фурье временной формы, когда в качестве простых функций выбирают гармонические колебания. Сущность этого представления состоит в следующем: любой электрический сигнал u(t) на произвольно заданном интервале времени длительностью Т от t = t0 до t = t0+T можно записать в виде суммы простых гармонических колебаний (ряда Фурье):
U0 – постоянная составляющая, В;
Umk – амплитуды гармоник, В;
ω1 – частота первой гармоники, рад/с;
φк – начальная фаза k-й гармоники.
Спектральная форма представления сигнала – это представление параметров сигнала в виде двух графиков:
· графика спектра амплитуд;
· графика спектра фаз.
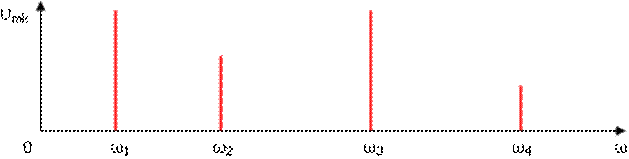
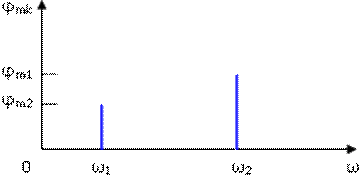
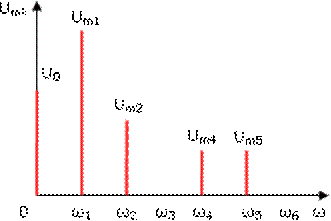
Спектральная диаграмма амплитуд показывает распределение энергии сигнала между составляющими его спектра. Пример такой диаграммы показан на рис. 1.4.2. Структура спектра периодического сигнала полностью определяется значениями амплитуд и фаз гармоник. Высота линий спектра амплитуд пропорциональна амплитуде данной гармоники, поэтому их высоты различны. Основание спектральной линии на оси частот лежит в точке, соответствующей частоте гармоники. Длины линий спектра фаз пропорциональны значению фаз. Основание спектральной линии на оси частот лежит в точке, соответствующей частоте гармоники.
Рисунок 1.4.2. График спектра амплитуд
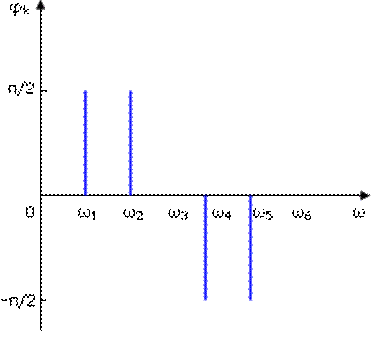
Рисунок 1.4.3. График спектра фаз
Периодические сигналы и их спектры
Математическая модель сигнала:
Параметрами гармонического сигнала являются:
· ω0 – угловая частота, рад/с;
· φ0 – начальная фаза, рад.
При построении графиков спектров более удобно угловую частоту ω0, рад/с перевести в линейную f0, Гц по формуле:
Рисунок 1.4.4. График спектра амплитуд
Рисунок 1.4.5. График спектра фаз
Вывод: гармонический сигнал имеет одну спектральную линию на графике спектра амплитуд и одну спектральную линию на графике спектра фаз.
Сложный периодический сигнал (бигармонический сигнал)
Рисунок 1.4.6. График спектра амплитуд
Рисунок 1.4.7. График спектра фаз
Вывод: сложный периодический сигнал имеет дискретный спектр.
Последовательность прямоугольных импульсов
В связи с тем, что последовательность прямоугольных импульсов является периодическим сигналом, его математическая модель может быть представлена рядом Фурье:
Данный ряд бесконечный, а каналов с бесконечной шириной полосы спектра не существует, поэтому его необходимо ограничить. Энергия гармоник, частоты которых попадают на интервал от 0 до 4*π/t (t – длительность импульса), составляет около 95% энергии этого сигнала на одном периоде. Длина этого периода равна ширине первых двух лепестков, что составляет 2*q гармоник (q = Т/t – скважность).
В качестве примера рассмотрим последовательность прямоугольных импульсов со скважностью q = 3 и построим спектр первых двух лепестков:
Рисунок 1.4.8. График спектра амплитуд
Рисунок 1.4.9. График спектра фаз
· последовательность прямоугольных импульсов имеет дискретный и бесконечный спектр;
· гармоники, частоты которых кратны скважности, обращаются в ноль;
· расстояние между линиями спектра равно частоте первой гармоники;
· гармоники, входящие в состав нечетных лепестков, имеют фазу (+π/2), а гармоники, входящие в состав четных лепестков, имеют фазу (-π/2).
Примечание: формулы для расчета параметров спектра будут даны в практической работе.
Непериодические сигналы и их спектры
Сигналы, не являющиеся периодическими, называются непериодическими. К ним относятся многие реальные сигналы электросвязи. Гармонический анализ периодических сигналов можно распространить на непериодические сигналы, если представить непериодический сигнал как периодический, но с периодом, стремящимся к бесконечности (Т→∞).
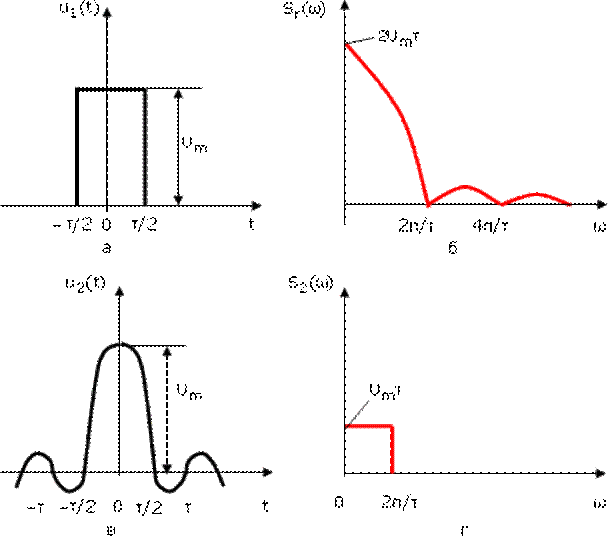
Рисунок 1.4.10. а, б – прямоугольный импульс и его спектральная плотность; в, г – затухающий импульс и его спектральная плотность
В этом случае частота первой гармоники стремится к нулю (f1 = 1/T = 1/∞→0), расстояния между линиями стремятся к нулю и спектр становится сплошным. Ниже приведены некоторые непериодические сигналы. Для непериодических сигналов рассматривается не спектр, а его производная по частоте, носящая название спектральной плотности.
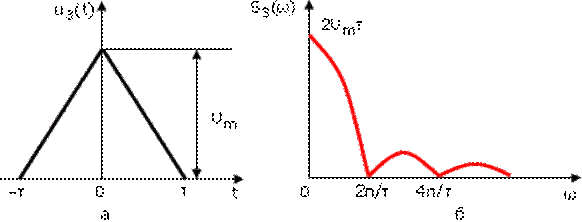
Рисунок 1.4.11. Треугольный импульс и его спектральная плотность а, б
Вывод: Периодические сигналы имеют сплошной спектр.
Тема 1.3. Классификация и основные характеристики сигналов электросвязи
Временная форма представления сигнала
Для более общего случая, когда дельта-функция отличается от нуля в момент времени t= 
(рис.1.3), имеем
Такая математическая модель соответствует абстрактному импульсу бесконечно малой длительности и безграничной величины. Единственным параметром, правильно отражающим реальный сигнал, является время его действия. Однако, учитывая (1.10), с помощью дельта-функции можно выразить значение реального сигнала u(t ) в конкретный момент времени ой:
Равенство (1.11) справедливо для любого текущего момента времени t. Заменив ой на t и приняв в качестве переменной интегрирования о, получим
Таким образом, функция u(t) выражена в виде совокупности примыкающих друг к другу импульсов бесконечно малой длительности. Ортогональность совокупности таких импульсов очевидна, так как они не перекрываются во времени.
Разложение (1.12) имеет большое значение в теории линейных систем, поскольку, установив реакцию системы на элементарный входной сигнал в виде дельта-функции (импульсную переходную функцию), можно легко определить реакцию системы на произвольный входной сигнал как суперпозицию реакций на бесконечную последовательность смещенных дельта-импульсов с «площадями», равными соответствующим значениям входного сигнала.
С помощью дельта-функций можно также представить периодическую последовательность идеализированных импульсов с постоянными или меняющимися уровнями. Обозначив через u
(t) функцию, равную u(k
t) в точках t = kt и нулю в остальных точках, запишем:
Релятивисты и позитивисты утверждают, что «мысленный эксперимент» весьма полезный интрумент для проверки теорий (также возникающих в нашем уме) на непротиворечивость. В этом они обманывают людей, так как любая проверка может осуществляться только независимым от объекта проверки источником. Сам заявитель гипотезы не может быть проверкой своего же заявления, так как причина самого этого заявления есть отсутствие видимых для заявителя противоречий в заявлении.
Эксперимент на то и эксперимент, что он есть не изощрение мысли, а проверка мысли. Непротиворечивая внутри себя мысль не может сама себя проверить. Это доказано Куртом Гёделем.
§ 1.3 Временная форма представления сигнала
Для более общего случая, когда дельта-функция отличается от нуля в момент времени t=
(рис.1.3), имеем
Такая математическая модель соответствует абстрактному импульсу бесконечно малой длительности и безграничной величины. Единственным параметром, правильно отражающим реальный сигнал, является время его действия. Однако, учитывая (1.10), с помощью дельта-функции можно выразить значение реального сигнала u(t) в конкретный момент времени ξι:
Равенство (1.11) справедливо для любого текущего момента времени t. Заменив ξι на t и приняв в качестве переменной интегрирования ξ, получим
Таким образом, функция u(t) выражена в виде совокупности примыкающих друг к другу импульсов бесконечно малой длительности. Ортогональность совокупности таких импульсов очевидна, так как они не перекрываются во времени.
Разложение (1.12) имеет большое значение в теории линейных систем, поскольку, установив реакцию системы на элементарный входной сигнал в виде дельта-функции (импульсную переходную функцию), можно легко определить реакцию системы на произвольный входной сигнал как суперпозицию реакций на бесконечную последовательность смещенных дельта-импульсов с «площадями», равными соответствующим значениям входного сигнала.
С помощью дельта-функций можно также представить периодическую последовательность идеализированных импульсов с постоянными или меняющимися уровнями. Обозначив через u
(t)функцию, равную u(k
t)в точках t = k
tи нулю в остальных точках, запишем:
§ 1.4 Частотная форма представления сигнала
Рассмотрим, какие функции целесообразно выбирать в качестве базисных при анализе инвариантных во времени линейных систем. При исследовании таких систем решения всегда содержат комплексные экспоненциальные функции времени. Детерминированные сигналы, описываемые экспоненциальными функциями времени, при прохождении через инвариантные во времени линейные системы не изменяются по своему характеру, что является следствием инвариантности класса экспоненциальных функций относительно операций дифференцирования и интегрирования.
Широко используются представления детерминированных сигналов с применением базисных функций еpt как при ρ = 
(преобразование Фурье), так и приp = s+j (обобщенное преобразование Фурье, известное как преобразование Лапласа).
До сих пор мы не касались физической интерпретации базисных функций. Для чисто математических преобразований она не обязательна. Однако такая интерпретация имеет безусловные преимущества, так как позволяет глубже вникнуть в физический смысл явлений, протекающих в системах при прохождении сигналов.
Использование экспоненциальных базисных функций в преобразовании Фурье комплексно-сопряженными парами (с положительным и отрицательным параметром ω) позволяет в соответствии с формулой Эйлера:
представить сложный детерминированный сигнал в виде суммы гармонических составляющих. Поскольку параметр ω в этом случае имеет смысл круговой частоты, результат такого преобразования называют частотной формой представления сигнала.
В силу указанных преимуществ разложение сигналов по системе гармонических базисных функций подверглось всестороннему исследованию, на основе которого была создана широко известная классическая спектральная теория сигналов.
В дальнейшем, если это не оговорено специально, спектральное представление сигналов рассматривается в рамках классической теории.
Спектры периодических сигналов. Периодических сигналов, естественно, не существует, так как любой реальный сигнал имеет начало и конец. Однако при анализе сигналов в установившемся режиме можно исходить из предположения, что они существуют бесконечно долго и принять в качестве математической модели таких сигналов периодическую функцию времени. Далее рассматривается представление таких функций, как в виде суммы экспоненциальных составляющих, так и с преобразованием их в гармонические.
Условия Дирихле: на любом конечном интервале функция должна быть непрерывной или иметь конечное число точек разрыва первого рода, а также конечное число экстремальных точек. В точках разрыва функцию u(t) следует считать равной.
Если в качестве базисных выбраны экспоненциальные функции, то выражение (1.5) запишем в виде
Соотношение (1.15) представляет собой ряд Фурье в комплексной форме, содержащий экспоненциальные функции как с положительным, так и с отрицательным параметром ω (двустороннее частотное представление). Составляющие с отрицательными частотами являются следствием комплексной формы записи вещественной функции.
Функцию A(jk1) принято называть комплексным спектром периодического сигнала u(t). Этот спектр дискретный, так как функция A(jk1) определена на числовой оси только для целых значений k. Значение функции A(jk1) при конкретном k называют комплексной амплитудой.
Огибающая комплексного спектра A(j) имеет вид
Запишем комплексный спектр в форме
Если известны спектр амплитуд и спектр фаз сигнала, то в соответствии с (1.15) он восстанавливается однозначно. В практических приложениях более значимым является спектр амплитуд, а информация о фазах составляющих часто несущественна.
Поскольку A(k1) и φ(k1) отличны от нуля только при целых k, спектры амплитуд и фаз периодического сигнала являются дискретными.
является четной функцией k, т.е.
Поскольку четность Ak и Вk, противоположна, спектр фаз
функция нечетная, т.е.
При k = 0 получаем постоянную составляющую
Учитывая соотношения (1.15) и (1.16), запишем
Воспользовавшись формулой Эйлера (1.14) и обозначив φ(k1) через φk, окончательно получим
Распространена и другая тригонометрическая форма ряда Фурье, имеющая вид
Однако она менее удобна для практического применения. Отдельные составляющие в представлениях (1.23) и (1.24) называют гармониками. Как спектр амплитуд, так и спектр фаз периодического сигнала удобно представлять наглядно спектральными диаграммами. На диаграмме спектра амплитуд каждой гармонике ставится в соответствие вертикальный отрезок, длина которого пропорциональна амплитуде, а расположение на оси абсцисс отвечает частоте этой составляющей. Аналогично на диаграмме спектра фаз обозначают значения фаз гармоник. Поскольку в результате спектры отображаются совокупностями линий, их часто называют линейчатыми.
Отметим, что дискретный (линейчатый) спектр не обязательно должен принадлежать периодическому сигналу. Спектр периодического сигнала характеризует совокупность гармоник, кратных основной частоте ωι. Линейчатые спектры, включающие гармоники некратных частот, принадлежат так называемым почти периодическим сигналам. Диаграмма спектра амплитуд периодического сигнала показана на рис.1.4 Огибающую A(t) этого спектра амплитуд можно получить, заменив k1 в A(k1) на ω, где ω = kω1 для k-й гармоники.
Пример 1.1 Определить спектры амплитуд и фаз периодической последовательности прямоугольных импульсов длительностью τ и амплитудой u0, следующих с частотой ω1 = 2π / Τ (рис.1.5).
Функция u(t), описывающая такую последовательность импульсов на периоде, может быть задана в виде:
В соответствии с (1.16) имеем
Амплитуды гармоник, включая постоянную составляющую, равную А0/2, определим из выражения
Выбор начала отсчета времени на их величину не влияет. Огибающая спектра амплитуд определяется видом функции
Характер изменения амплитуд диктуется функцией sin х / х и не зависит от частоты следования импульсов. На частотах, кратных 2π / τ, огибающая спектра равна нулю.
На рис.1.6 приведена диаграмма спектра амплитуд для случая
Τ / τ = 3 [ω1 = 2π / (3τ)]. Число составляющих в спектре бесконечно велико. Крутизна фронтов импульсов обусловлена наличием в спектре составляющих с частотами, существенно превышающими основную частоту ω1.
Опираясь на формулу (1.29) и принимая во внимание, что знаки функции sin(k1
/ 2) на последовательности интервалов частотΔω = 2π / τ чередуются, выражение для спектра фаз запишем следующим образом:
Спектр фаз зависит от выбора начала отсчета. Если передний фронт прямоугольного импульса последовательности приходится на начало отсчета времени, то на каждом интервале Δω = 2π / τ фазы составляющих возрастают линейно. Диаграмма спектра фаз последовательности прямоугольных импульсов для этого случая (Τ / τ = 3, t1 = 0) показана на рис.1.7
Пример 1.2 Вычислить несколько первых членов ряда Фурье для периодической последовательности прямоугольных импульсов и проследить, как их гумма сходится к указанному сигналу.
Воспользуемся результатами предыдущего примера для случая широко используемой на практике периодической последовательности импульсов, у которых длительность τ равна половине периода Т. Примем также t1 = 0.
Суммируя указанные составляющие, получим последовательность импульсов (рис.1.8), отличающихся от прямоугольных в основном недостаточно высокой крутизной фронтов.
Отметим, что крутизна фронтов импульсов обусловлена наличием в их спектре составляющих с частотами, многократно превышающими основную частоту.
Распределение энергии в спектре. Рассмотрим, как распределяется энергия сложного периодического сигнала u(t) по его спектральным составляющим. Под временной функцией u(t) будем подразумевать электрическое напряжение на резисторе в 1 Ом. Энергия WT, выделяемая на этом резисторе за время, равное периоду колебаний Т,
Используя спектральное представление u(t) в виде ряда Фурье (1.15), получим
Определим значения интегралов в выражении (1.35):
Так как A(jk1) и А(-jk1) комплексно сопряжены, то
С учетом (1.28) и (1.29) выражение для WT существенно упрощается:
Из (1.38) следует, что средняя за период энергия сложного периодического сигнала равна сумме средних энергий, выделяемых на резисторе в 1 Ом каждой его гармоникой в отдельности (включая постоянную составляющую).
С течением времени выделяемая энергия безгранично растет, при этом средняя мощность остается постоянной:
Важно отметить, что она не зависит от фаз отдельных гармоник и, следовательно, будет сохранять свое значение при изменениях формы сигнала, обусловленных нарушениями фазовых соотношений гармоник спектра.
Пример 1.3 Определим, какая часть средней мощности, выделяемой на резисторе с сопротивлением в 1 Ом, периодической последовательностью прямоугольных импульсов с параметрами из примера 1.2 приходится на пять первых гармоник и постоянную составляющую.
Значения амплитуд составляющих определены ранее (см. табл.11). Подставляя их в (1.39), для средней мощности Р5 сигнала, включающего указанные составляющие, получим
Так как средняя мощность последовательности прямоугольных импульсов при τ= Т / 2 равна 0,5 
, то искомая часть составляет 96% от этой мощности.
Область частот, в которой сосредоточена подавляющая часть мощности периодического сигнала, называют практической шириной его спектра. Если не предъявляется жестких требований относительно крутизны фронтов импульсов (см. пример 1 2), расширение этой области нецелесообразно.
Спектры непериодических сигналов. Любой физически реализуемый сигнал ограничен во времени и обладает конечной энергией. Функции, отображающие реальные сигналы, удовлетворяют условиям Дирихле и абсолютно интегрируемы, т.е.
Модели таких сигналов также могут быть представлены совокупностью гармонических составляющих в соответствии с выражением (1.2). Конкретный вид спектрального преобразования для непериодического сигнала получим, проследив изменения, происходящие в спектре периодической последовательности импульсов u1(t) при увеличении периода их повторения.
В соответствии с формулой (1.30), которая справедлива для любого значения периода Т, абсолютные значения амплитуд спектральных составляющих в (1.27) при увеличении периода уменьшаются. Так как частоты составляющих спектра кратны основной частоте, то при ее уменьшении линии на спектральной диаграмме сближаются.
Спектральное представление для одиночного импульса u(t) получим как следствие увеличения периода сигнала u1(t) до бесконечности.
Пару преобразований Фурье для периодической функции u1(t) запишем в форме (1.15) и (1.16):
При T 
u1(t) переходит в u(t), частота ω1 уменьшается до d, а k1 превращается в текущую частоту ω. Заменяя суммирование интегрированием, находим
Обозначив интеграл в квадратных скобках S(jω), получим формулы для прямого и обратного интегрального преобразования Фурье:
Величину S(jω) называют комплексной спектральной плотностью или спектральной характеристикой. Она имеет размерность [амплитуда / частота]. На каждой конкретной частоте амплитуда соответствующей составляющей равна нулю. Сравнивая (1.15) и (1.42), находим, что бесконечно малому интервалу частоты dω соответствует составляющая с бесконечно малой комплексной амплитудой dA(j):
Сравнение выражения (1.41) для спектральной характеристики функции u(t), заданной на интервале времени 
, с формулой (1.17) для огибающей комплексного спектра такой же функции, периодически продолжающейся во времени, показывает, что они различаются только множителем:
Как комплексная величина спектральная характеристика может быть записана в виде
где S(ω) = |S(jω) | называется спектральной плотностью амплитуд или спектром непериодического сигнала.
Так как составляющие расположены на всех частотах, то спектр непериодического сигнала является непрерывным или сплошным. Представим спектральную характеристику состоящей из действительной и мнимой частей:
Модуль спектральной характеристики S(ω) определяется выражением
и представляет собой четную функцию частоты.
Для фазы спектральной характеристики S(jω) соответственно получаем
Комплексная форма интегрального преобразования Фурье легко приводится к тригонометрической:
Второй член в связи с нечетностью подынтегрального выражения равен нулю. Окончательно имеем
Преимущество тригонометрической формы записи Фурье-преобразования заключается в возможности некоторого физического толкования с использованием идеализации, не очень далеких от реальности.
Пример 1.4 Найти спектр одиночного прямоугольного импульса, описываемого функцией времени (рис.1.9):
Выражение для спектральной характеристики амплитуд находим в соответствии с (1.41)
Искомый спектр представляет собой модуль этого выражения:
Спектр одиночного прямоугольного импульса (рис.1.10), естественно [см. (1.44)], имеет ту же форму, что и огибающая периодической последовательности таких импульсов (см. рис.1.6).
Пример 1.5 Определить спектр дельта-функции [см. соотношения (1.10) и рис.1.3].
Запишем выражение для спектральной характеристики S(j) дельта-функции, сосредоточенной в точке 
:
В соответствии с (1.11) имеем
откуда модуль спектральной характеристики
Следовательно, дельта-функции соответствует сплошной равномерный спектр, включающий в себя составляющие бесконечно больших частот (рис.1.11). При ξι = 0 начальные фазы всех составляющих равны нулю.
Распределение энергии в спектре. Рассмотрим непериодический сигнал u(t), физическим представлением которого будем считать электрическое напряжение на резисторе с сопротивлением в 1 Ом.
Тогда энергия, выделяемая на этом резисторе
В предположении, что интеграл (1.54) сходится, выразим энергию через модуль спектральной характеристики S(ω) сигнала u(t). Квадрат этого модуля запишем в виде
функция, комплексно-сопряженная спектральной характеристике S(jω) сигнала u(t). Тогда
После изменения последовательности интегрирования и использования обратного преобразования Фурье (1.42) получим
Соотношение (1.56) известно как равенство Парсеваля. Оказывается, что энергию, выделяемую непериодическим сигналом за время его существования, можно определить, интегрируя квадрат модуля его спектральной характеристики в интервале частот.
Каждое из бесконечно малых слагаемых (1/π) |S(ω) |2dω, соответствующих бесконечно малым участкам спектра, характеризует энергию, приходящуюся на спектральные составляющие сигнала, сосредоточенные в полосе частот от ω до ω + dω.
Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.