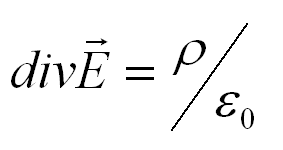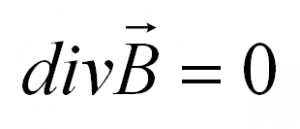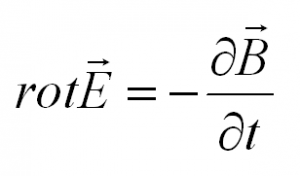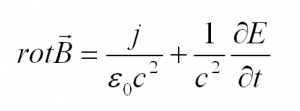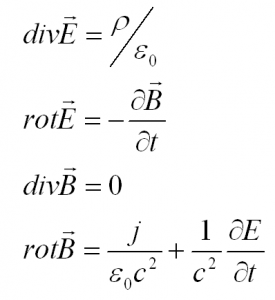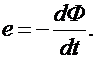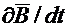второе уравнение максвелла в дифференциальной форме

Система уравнений Максвелла для электромагнитного поля: смысл, способы решения

Уравнения Максвелла в электродинамике – это как законы Ньютона в классической механике или как постулаты Эйнштейна в теории относительности. Фундаментальные уравнения, в сущности которых мы сегодня будем разбираться, чтобы не впадать в ступор от одного их упоминания.

Полезная и интересная информация по другим темам – у нас в телеграм.

Уравнения Максвелла – это система уравнений в дифференциальной или интегральной форме, описывающая любые электромагнитные поля, связь между токами и электрическими зарядами в любых средах.

Уравнения Максвелла неохотно принимались и критически воспринимались учеными-современниками Максвелла. Все потому, что эти уравнения не были похожи ни на что из известного людям ранее.

Тем не менее, и по сей день нет никаких сомнений в правильности уравнений Максвелла, они «работают» не только в привычном нам макромире, но и в области квантовой механики.

Уравнения Максвелла совершили настоящий переворот в восприятии людьми научной картины мира. Так, они предвосхитили открытие радиоволн и показали, что свет имеет электромагнитную природу.

Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.

По порядку запишем и поясним все 4 уравнения. Сразу уточним, что записывать их будем в системе СИ.

Первое уравнение Максвелла

Современный вид первого уравнения Максвелла таков:

Тут нужно пояснить, что такое дивергенция. Дивергенция – это дифференциальный оператор, определяющий поток какого-то поля через определенную поверхность. Уместным будет сравнение с краном или с трубой. Например, чем больше диаметр носика крана и напор в трубе, тем большим будет поток воды через поверхность, которую представляет собой носик.

В первом уравнении Максвелла E – это векторное электрическое поле, а греческая буква «ро» – суммарный заряд, заключенный внутри замкнутой поверхности.

Так вот, поток электрического поля E через любую замкнутую поверхность зависит от суммарного заряда внутри этой поверхности. Данное уравнение представляет собой закон (теорему) Гаусса.

Третье уравнение Максвелла

Сейчас мы пропустим второе уравнение, так как третье уравнение Максвелла – это тоже закон Гаусса, только уже не для электрического поля, но для магнитного.

Что это значит? Поток магнитного поля через замкнутую поверхность равен нулю. Если электрические заряды (положительные и отрицательные) вполне могут существовать по отдельности, порождая вокруг себя электрическое поле, то магнитных зарядов в природе просто не существует.

Второе уравнение Максвелла

Второе уравнение Максвелла представляет собой ни что иное, как закон Фарадея. Его вид:

Ротор электрического поля (интеграл через замкнутую поверхность) равен скорости изменения магнитного потока, пронизывающего эту поверхность. Чтобы лучше понять, возьмем воду в ванной, которая сливается через отверстие. Вокруг отверстия образуется воронка. Ротор – это сумма (интеграл) векторов скоростей частиц воды, которые вращаются вокруг отверстия.

Как Вы помните, на основе закона Фарадея работают электродвигатели: вращающийся магнит порождает ток в катушке.

Четвертое уравнение Максвелла

Это уравнение еще называется теоремой о циркуляции вектора магнитной индукции. Оно говорит нам о том, что электрический ток и изменение электрического поля порождают вихревое магнитное поле.

Приведем теперь всю систему уравнений и кратко обозначим суть каждого из них:

Первое уравнение: электрический заряд порождает электрическое поле

Второе уравнение: изменяющееся магнитное поле порождает вихревое электрическое поле

Третье уравнение: магнитных зарядов не существует

Четвертое уравнение: электрический ток и изменение электрической индукции порождают вихревое магнитное поле

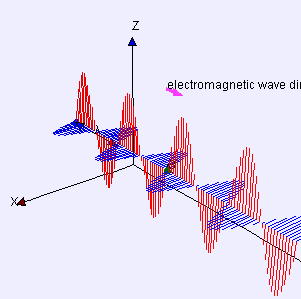
Решая уравнения Максвелла для свободной электромагнитной волны, мы получим следующую картину ее распространения в пространстве:

Надеемся, эта статья поможет систематизировать знания об уравнениях Максвелла. А если понадобиться решить задачу по электродинамике с применением этих уравнений, можете смело обратиться за помощью в студенческий сервис. Подробное объяснение любого задания и отличная оценка гарантированы.

Источник

Уравнения Максвелла

Уравнения Максвелла — это 4 уравнения, которые описывают, как электрические и магнитные поля распространяются и взаимодействуют; т.е. эти уравнения (правила или даже законы) описывают процессы/взаимодействия электромагнетизма.

Эти правила описывают, как проходит управление поведением электрических и магнитных полей. Уравнения Максвелла показывают, что электрический заряд (положительный и отрицательный):

Уравнения Максвелла в дифференциальной форме

Уравнение 1: Закон Гаусса или Теорема Гаусса

Дивергенция электрического поля равняется плотности заряда. Существует вязь между электрическим полем и электрическим зарядом.

Дивергенция в физике показывает, насколько данная точка пространства является источником или потребителем потока поля.

Очень кратко: Электрические поля расходятся от электрических зарядов: электрический заряд создаёт поле вокруг себя и, таким образом, действует как источник электрических полей. Это можно сравнить с краном, который является источником воды.

Ещё закон Гаусса говорит о том, что отрицательные заряды действуют как сток для электрических полей (способ, как вода стекает через отверстие стока). Это означает, что линии электрического поля имеют начало и поглощаются при электрическом заряде.

Заряды с одинаковым знаком отталкиваются друг от друга, а противоположные заряды притягиваются друг к другу (если есть два положительных заряда, они будут отталкиваться; а если есть один отрицательный и один положительный, они будут притягиваться друг к другу).

Уравнение 2: Закон электромагнитной индукции (Закон Фарадея)

Можно создать электрическое поле, изменив магнитное поле.

Очень кратко: Закон Фарадея гласит, что изменяющееся магнитное поле внутри контура вызывает индуцированный ток, который возникает из-за силы или напряжения внутри контура. Это значит:

Уравнение 3: Закон Гаусса для магнетизма

Дивергенция магнитного потока любой замкнутой поверхности равна нулю. Магнитного монополя не существует.

Закон Гаусса для магнетизма утверждает (очень кратко):

Уравнение 4: Закон Ампера

Магнитное поле создаётся с помощью тока или изменяющегося электрического поля.

Очень кратко: Электрический ток порождает магнитное поле вокруг тока. Изменяющийся во времени электрический поток порождает магнитное поле.

Уравнения Максвелла в интегральной и дифференциальной форме

Вспомним сначала в дифференциальной форме и следом будет в интегральной форме.

Уравнение 1: Закон Гаусса (Теорема Гаусса)

Это же уравнение в интегральной форме:

Поток вектора электрической индукции D через любую замкнутую поверхность равняется сумме свободных зарядов, охваченных этой поверхностью. Электрическое поле создаётся нескомпенсированными электрическими зарядами (это те, что создают вокруг себя своё собственное электрическое поле).

Уравнение 2: Закон электромагнитной индукции (Закон Фарадея)

И это же уравнение в интегральной форме:

Циркуляция вектора напряжённости Е вихревого электрического поля (по любому замкнутому контуру) равняется скорости изменения магнитного потока через площадь контура (S) с противоположным знаком.

Уравнение 3: Закон Гаусса для магнетизма

И это же уравнение в интегральной форме:

Силовые линии магнитного поля замкнуты, т.к. поток вектора индукции В магнитного поля через любую замкнутую поверхность равняется нулю.

Уравнение 4: Закон Ампера

И это же уравнение в интегральной форме:

Циркуляция вектора напряжённости Н магнитного поля по замкнутому контуру равняется алгебраической сумме токов, которые пронизывают этот контур. Магнитное поле создаётся не только током проводимости, но и переменным электрическим полем.

Источник

Второе уравнение Максвелла

Определение переменного электромагнитного поля

Под переменным электромагнитным полем понимают совокупность изменяющихся во времени и взаимно связанных и обуславливающих друг друга электрического и магнитного полей. Оно определяется двумя векторными величинами – напряженностью электрического поля и напряженностью магнитного поля .

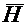
Переменное электромагнитное поле является одним из видов материи. Оно обладает энергией, массой, количеством движения, может превращаться в другие виды материи и самостоятельно существовать в виде электромагнитных волн. Любые возмущения поля в диэлектрике с огромной скоростью, для вакуума равной примерно 3·10 8 м/с, передаются на большие расстояния.

При исследовании процессов в переменном электромагнитном поле пользуются уравнениями Максвелла.

Первое уравнение Максвелла

Первое уравнение Максвелла представляет собой закон полного тока в дифференциальной форме

(44.1)

Так как плотность полного тока определяется суммой плотности тока проводимости и плотности тока смещения , то первое уравнение Максвелла в общем случае имеет вид:

(44.2)

Для сред с постоянной диэлектрической проницаемостью

(44.3)

Физический смысл этого уравнения заключается в том, что вихревое магнитное поле возбуждается как токами проводимости, так и изменяющимся во времени электрическим полем.

Для идеальных диэлектриков с проводимостью имеем:

(44.4)

Первое уравнение Максвелла устанавливает зависимость между изменением во времени напряженности электрического поля и изменением в пространстве напряженности магнитного поля и указывает на то, что электромагнитное поле всегда находится в движении.

Второе уравнение Максвелла

Второе уравнение Максвелла представляет собой дифференциальную форму закона электромагнитной индукции, согласно которому в витке при изменении сцепленного с ним магнитного потока наводится ЭДС, равная

Максвелл обобщил этот закон, указав, что изменяющийся во времени магнитный поток возбуждает электрическое поле и при отсутствии витка.

В поле с индукцией магнитный поток сквозь произвольную поверхность S, ограниченную контуром L, равен:

Если напряженность индуцированного электрического поля обозначить Е, то наведенная в контуре ЭДС .

Будем считать, что контур L и поверхность S неподвижны и не деформируются, тогда

Положительные направления обхода контура L и положительное направление нормали к поверхности S выбираются так, чтобы они образовали правовинтовую систему.

Частные производные введены потому, что ЭДС может индуцироваться не только за счет изменения магнитного потока во времени, но и за счет движения или деформации контура.

На основании теоремы Стокса можно преобразовать циркуляцию

Равенство интегралов справедливо для любой поверхности S, поэтому подынтегральные функции равны и

(44.5)

Полученное выражение называют вторым уравнением Максвелла.

Физический смысл его заключается в утверждении, что изменяющееся во времени магнитное поле возбуждает вихревое электрическое поле.

Так как 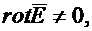то линии вектора могут быть замкнутыми, причем они должны охватывать линии вектора . Направление линий векторов и показаны на рисунке 44.1 для случая, когда

Источник

Второе уравнение максвелла в дифференциальной форме

Теория Д.К. Максвелла лежит в основе объяснения существования и свойств любых электромагнитных волн, таких, как световые волны, радиоволны, инфракрасное и ультрафиолетовое излучения. Эта теория является феноменологической, т.е. в ней не рассматриваются молекулярное строение среды и внутренний механизм процессов, происходящих в среде под действием электрического и магнитного полей. Электрические и магнитные свойства среды характеризуются относительной диэлектрической проницаемостью ε, относительной магнитной проницаемостью m и удельной электрической проводимостью σ. Предполагается, что эти параметры среды определяются из эксперимента.

Дифференциальные уравнения Максвелла получаются из интегральных с помощью двух теорем векторного анализа: теоремы Остроградского-Гаусса и теоремы Стокса.

Операция дивергенции над произвольным вектором сводится к пространственной производной вида:

(4.1.2)

Векторная операция rot в декартовых координатах выражается так:

(4.1.4)

Первое уравнение Максвелла

Это уравнение представляет собой обобщение закона электромагнитной индукции Фарадея:

(4.1.5)

Однако для произвольного контура выполняется взаимосвязь:

(4.1.6)

Сравнивая (4.1.5) и (4.1.7) с учетом (4.1.6), для произвольного контура L, мысленно проведенного в переменном магнитном поле, можно записать:

(4.1.8)

Используя теорему Стокса, преобразуем (4.1.5):

(4.1.9)

Сравнивая подинтегральные выражения в (4.1.7) и в правой части (4.1.9), получим окончательно первое уравнение Максвелла в дифференциальной форме:

(4.1.10)

Физический смысл этого уравнения: переменное магнитное поле индуцирует вихревое электрическое поле.

Второе уравнение Максвелла

Используем теорему Гаусса для диэлектриков:

(4.1.11)

Продифференцируем (4.1.11) по времени:

(4.1.12)

Правая часть этой формулы имеет размерность тока, следовательно, величина имеет размерность плотности тока. Максвелл предложил назвать эту величину плотностью тока смещения :

(4.1.14)

Введя представление о токе смещения, Максвелл по-новому подошел к рассмотрению условия замкнутости цепей электрического тока. Как известно, цепи постоянного тока должны быть замкнутыми. Однако для цепей переменного тока это условие уже не является обязательным. Например, при зарядке и разрядке конденсатора постоянный электрический ток протекает по проводнику, соединяющему обкладки, но не проходит через диэлектрик, находящийся между обкладками. Следовательно, цепь не замкнута. Однако, с точки зрения Максвелла, для переменного тока такая цепь замыкается благодаря току смещения, который протекает через такой участок, где нет проводника, т.е. через диэлектрик. На таком участке благодаря наличию переменного тока смещения обязательно возникает переменное магнитное поле. Однако действие тока смещения, приводящее к возникновению магнитного поля, нельзя отделить от действия обычного тока проводимости. Например, для прямолинейного тока проводимости можно записать:

(4.1.15)

Линии магнитного поля направлены по касательным к концентрическим окружностям, окружающим проводник с током. Найдем циркуляцию магнитного поля по замкнутому контуру в виде окружности радиуса r:

(4.1.16)

Максвелл предположил, что в правой части соотношения (4.1.16) следует добавить ток смещения:

(4.1.17)

где ток смещения легко вычислить, используя (4.1.14):

(4.1.18)

Силу тока проводимости можно также представить в виде:

(4.1.19)

Согласно теореме Стокса для магнитного поля, имеем:

(4.1.20)

Подставляя (4.1.18) и (4.1.19) в (4.1.17) и сравнивая подинтегральные выражения в правой и левой частях, получаем второе уравнение Максвелла:

(4.1.21)

При отсутствии тока проводимости, тем не менее, может существовать переменное магнитное поле, обусловленное только током смещения:

(4.1.22)

Третье уравнение Максвелла

Максвелл обобщил теорему Гаусса для диэлектриков (4.1.11), предположив, что она справедлива для любого электрического поля, как стационарного, так и переменного. Запишем уравнение (4.1.11) в виде:

(4.1.23)

Тогда, используя теорему Остроградского-Гаусса для вектора электрической индукции, получим:

(4.1.24)

Сравнивая подинтегральные выражения в (4.1.23) и (4.1.24), получим третье уравнение Максвелла:

(4.1.25)

Четвертое уравнение Максвелла

Поскольку поток вектора магнитной индукции равен нулю:

(4.1.26)

то, используя теорему Остроградского-Гаусса для вектора магнитной индукции, легко получить четвертое уравнение Максвелла:

(4.1.27)

Такое равенство определяется отсутствием магнитных зарядов.

Итак, полная система уравнений Максвелла в дифференциальной форме включает в себя четыре дифференциальных уравнения:

(4.1.28)

В случае изотропных несегнетоэлектрических и неферромагнитных сред и макроскопических токов, подчиняющихся закону Ома, эти уравнения в системе СИ имеют вид:

(4.1.29)

4.1.2. Свойства электромагнитных волн

Существование электромагнитных волн непосредственно следует их уравнений Максвелла. Для области пространства, не содержащей свободных электрических зарядов и макроскопических токов, эти уравнения приобретают вид:

(4.1.30)

Используя материальные уравнения (4.1.29), эти уравнения можно представить в виде:

(4.1.31)

Если записать эти уравнения в проекциях на оси декартовой системы координат, то получим:

Используя первое из уравнений (4.1.33), можно получить:

(4.1.35)

Следовательно, компонента Е_х удовлетворяет волновому уравнению:

(4.1.36)

Если ввести обозначение для дифференциальной операции:

(4.1.37)

то волновое уравнение (4.1.37) можно представить в компактном виде:

(4.1.38)

Аналогичные уравнения могут быть получены и для всех других компонент электрического и магнитного полей. Суммируя результаты, окончательно можно представить волновые уравнения для электрического и магнитного полей в векторном виде:

(4.1.39)

Таким образом, переменное электромагнитное поле распространяется в среде в виде волн, фазовая скорость которых равна:

(4.1.40)

есть скорость электромагнитной волны в вакууме.

Прямой проверкой можно показать, что решениями уравнений (4.1.39) служат плоские синусоидальные волны, которые удобно представить в форме Эйлера:

(4.1.42)

Операция ротора может быть сведена к векторному произведению, например:

(4.1.43)

Тогда, используя решения (4.1.42), с помощью (4.1.43) имеем:

(4.1.44)

следовательно, применение этой операции сводится к векторному произведению.

Рассмотрим сейчас операцию:

(4.1.45)

Наконец, операцию дивергенции можно представить так:

(4.1.46)

Применяя результаты (4.1.44), (4.1.45) и (4.1.46) к уравнениям Максвелла (4.1.31), имеем:

или, окончательно:

(4.1.47)

4.1.3. Шкала электромагнитных волн

Оптическим излучением или светом называются электромагнитные волны, у которых длина волны в вакууме лежит в диапазоне 10 нм >λ₀ > 1 мм (границы условны). К оптическому излучению относят инфракрасное, видимое и ультрафиолетовое излучения.

Инфракрасным (ИК) называются электромагнитные волны, испускаемые нагретыми телами, у которых длина волны в вакууме лежит в диапазоне 1 мм > λ₀ > 770 нм.

Видимым излучением (светом) называются электромагнитные волны, у которых длины волны в вакууме лежат в диапазоне 770 нм > λ₀ > 380 нм. Свет способен вызывать зрительные ощущения в человеческом глазе.

Ультрафиолетовым излучением (УФ) называются электромагнитные волны, у которых длины волны в вакууме лежат в диапазоне 380 нм > λ₀ > 10 нм.

Рентгеновским излучением (рентгеновскими лучами) называются электромагнитные волны, которые возникают при взаимодействии заряженных частиц и фотонов с атомами вещества. Оно характеризуется длинами волны в вакууме в диапазоне с условными границами (10-100 нм) > λ₀ > (0,01-1 пм).

Гамма-излучением (γ-лучами) называются электромагнитные волны с длинами волны в вакууме 0,1 нм > λ₀. Это излучение испускается возбужденными атомными ядрами при радиоактивных превращениях и ядерных реакциях, а также возникает при распаде частиц, аннигиляции пар «частица-античастица» и других процессах.

4.1.4. Световая волна

Отношение скорости световой волны в вакууме с к ее фазовой скорости v в некоторой прозрачной среде называется абсолютным показателем преломления этой среды:

(4.1.49)

Показатель преломления связан с относительными диэлектрической и магнитной проницаемостями соотношением:

(4.1.50)

Для подавляющего большинства прозрачных веществ величина μ &#8776 1. Поэтому можно считать, что выполняется:

(4.1.51)

Значения показателя преломления характеризуют оптическую плотность среды. Среда с большим n будет более оптически плотной.

Длины волн видимого света в вакууме заключены в пределах:

(4.1.52)

В веществе длины волн будут другими. В случае колебаний с частотой ν длина волны света в вакууме равна:

(4.1.53)

Используя соотношение (4.1.49), имеем для длины света в веществе формулу:

(4.1.54)

Частоты видимого света лежат в пределах:

(4.1.55)

Модуль среднего по времени потока энергии, переносимого волной, называется интенсивностью света I в данной точке пространства. Интенсивность пропорциональна квадрату амплитуды волны:

I ∼ A 2

(4.1.56)

4.1.5. Геометрическая оптика

Следовательно, время τ, необходимое для прохождения пути от точки 1 до точки 2 (Рис. 4.1.2), равно:

(4.1.58)

Рис. 4.1.2. К принципу Ферма

Имеющая размерность длины величина

(4.1.59)

Следовательно,

(4.1.61)

Пропорциональность времени прохождения оптической длине пути дает возможность сформулировать принцип Ферма так: свет распространяется по такому пути, оптическая длина которого минимальна.

Из принципа Ферма вытекает обратимость световых лучей. Действительно, оптический путь, который минимален при движении света из точки 1 в точку 2, окажется минимальным и в случае распространения света в обратном направлении.

Получим с помощью принципа Ферма законы отражения и преломления света. Пусть свет попадает из точки А в точку В, отразившись от поверхности MN (Рис. 4.1.3).

Рис. 4.1.3. Закон отражения света как следствие принципа Ферма

Прямой путь из А в В прегражден экраном Э. Среда, в которой распространяется луч, однородна, поэтому минимальность оптической длины пути сводится к минимальности геометрической длины пути. Геометрическая длина произвольно взятого пути равна АО’B = A’O’B, поскольку вспомогательная точка A’ является зеркальным отражением точки А, и АО’ = A’O’. Из Рис. 4.1.3 видно, что наименьшей длиной обладает путь луча, отразившегося в точке О, для которой угол отражения равен углу падения. При удалении точки O’ от точки О геометрическая длина пути неограниченно возрастает, что противоречит принципу Ферма. Этот результат можно записать так:

(4.1.62)

Соотношение (4.1.62) выражает закон отражения света : отраженный луч лежит в одной плоскости с падающим лучом и нормалью, восстановленной в точке падения; угол отражения равен углу падения.

Найдем точку, в которой должен преломиться луч, распространяясь от А к В, чтобы оптическая длина пути была минимальной (Рис. 4.1.4).

Рис. 4.1.4. К расчету закона преломления света из принципа Ферма

Для произвольного луча оптическая длина пути равна:

(4.1.63)

Чтобы найти минимальное значение оптической длины пути, продифференцируем L по х и приравняем производную к нулю:

(4.1.64)

Множители при n₁ и n₂ равны, соответственно, sinθ и sinθ». Поэтому получаем соотношение:

(4.1.65)

которое выражает закон преломления света. Используя взаимосвязь показателей преломления с фазовыми скоростями распространения света в средах, можно записать соотношение (4.1.65) в виде:

(4.1.66)

Следовательно, закон преломления света гласит: преломленный луч лежит в одной плоскости с падающим лучом и нормалью; отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных веществ.

При углах падения, лежащих в пределах от θ_пред пред до 90°, преломленной волны не существует, вся энергия падающей волны переходит в энергию отраженной волны. Это явление называется полным внутренним отражением.

Показатели преломления некоторых веществ при λ=0,589 мкм

Вещество	Показатель преломления	Вещество	Показатель преломления
Воздух	1,0003	Стекло (крон)	1,515
Вода	1,333	Стекло (флинт)	1,752
Спирт (этиловый)	1,362	Алмаз	2,420

Во многих оптических приборах для преломления света используются стеклянные призмы. На Рис. 4.1.5 показан ход луча монохроматического света в призме.

Рис. 4.1.5. Ход лучей в призме

При малых углах α и θ углы α₁, γ и γ₁ также малы. Поэтому вместо (4.1.69) можно приближенно записать:

(4.1.70)

Угол δ из треугольника BED равен:

(4.1.73)

Подставляя в (4.1.72) результаты (4.1.73) и (4.1.70), получим окончательно:

(4.1.74)

4.1.6. Преломление в линзе

Рассмотрим линзу, ограниченную двумя сферическими преломляющими поверхностями PO₁Q и PO₂Q (Рис. 4.1.6).

Рис. 4.1.6. Тонкая линза

Покажем, что лучи, исходящие под небольшими углами α из некоторой точки А, лежащей на главной оптической оси, собираются линзой в одну точку А₁, расположенную также на этой оптической оси и называемую изображением точки А (Рис. 4.1.7).

Рис. 4.1.7. Преломление в тонкой линзе

Построим плоскости, касательные к поверхностям линзы в точках М и N (в местах падения луча на линзу и его выхода из линзы), и проведем в эти точки радиусы R₁ и R₂ кривизны поверхностей линзы. Тогда луч AMNA₁ можно рассматривать как луч, преломленный в тонкой призме с преломляющим углом θ. Учитывая малость углов α, β, α₁, β₁ и толщины линзы, можно записать:

(4.1.75)

Из треугольников АНА₁ и ВЕВ₁ следует, что:

(4.1.76)

Принимая во внимание формулы (4.1.75), получим:

(4.1.77)

Учтено, что для тонкой линзы h₁ ≈ h₂ ≈ h. Поскольку, согласно формуле (4.1.74) для тонкой призмы выполняется: θ = (n-1)δ, то, с помощью (4.1.77) имеем формулу линзы :

(4.1.78)

Если точка А находится бесконечно далеко от линзы (а = ∞), т.е. если лучи падают на линзу параллельно главной оптической оси, то, согласно формуле (4.1.78), имеем:

(4.1.79)

Величина b = f называется фокусным расстоянием линзы :

(4.1.80)

Фокусом линзы называется точка, в которой после преломления собираются все лучи, падающие на линзу параллельно главной оптической оси.

Принимая во внимание (4.1.80), формулу линзы (4.1.78) можно сейчас переписать так:

(4.1.81)

Величина, обратная фокусному расстоянию, называется оптической силой линзы :

(4.1.82)

4.1.7. Принцип Гюйгенса

В приближении геометрической оптики свет за преградой не должен проникать в область геометрической тени. В действительности световая волна распространяется во всем пространстве за преградой, проникая проникать в область геометрической тени, причем это проникновение будет тем более существенным, чем меньше размеры отверстия. При диаметре отверстия или ширине щели, сравнимых с длиной волны, приближение геометрической оптики становится совершенно неприменимым.

Рис. 4.1.8. К принципу Гюйгенса

Согласно Гюйгенсу, каждая точка выделяемого отверстием участка волнового фронта служит центром вторичных волн, которые в однородной и изотропной среде будут сферическими. Построив огибающую вторичных волн, можно убедиться в том, что за отверстием волна проникает в область геометрической тени, огибая края преграды.

4.1.8. Интерференция световых волн

Если в среде распространяются одновременно несколько электромагнитных волн, то волны просто накладываются друг на друга, не возмущая одна другую. Это утверждение, подкрепленное опытом, называется принципом суперпозиции.

Пусть две волны одинаковой частоты, распространяющиеся в одном направлении, возбуждают в некоторой точке пространства колебания:

(4.1.83)

Эти векторы можно представить как вращающиеся с частотой ω вокруг общего начала коор-динат. Поскольку сдвиг фаз различен, в какой-либо момент времени эти вектора займут различные положения (Рис. 4.1.9).

Рис. 4.1.9. К расчету интерференции волн

Используя теорему косинусов, получим амплитуду результирующего колебания:

(4.1.84)

Когерентные световые волны можно получить, разделив, например, с помощью зеркал волну, излучаемую одним источником, на две. Если заставить эти волны пройти разные пути, а затем наложить их друг на друга, будет наблюдаться интерференция. Пусть такое разделение происходит в точке О (Рис. 4.1.10).

Рис. 4.1.10. Образование когерентных волн

До точки Р первая волна пройдет в среде с показателем преломления n₁ путь S₁, вторая волна пройдет в среде с показателем преломления n₂ путь S₂. Если в точке О фаза колебания была равна ωt, то первая волна возбудит в точке Р колебание

(4.1.87)

Поскольку выполняется:

(4.1.90)

то, подставляя (4.1.90) в (4.1.8), для сдвига фаз имеем выражение:

(4.1.91)

есть величина, называемая оптической разностью хода и равная разности оптических длин проходимых волнами путей в средах с различными показателями преломления.

Из (4.1.91) следует, что если оптическая разность хода равна целому числу длин волн в вакууме:

(4.1.93)

то разность фаз оказывается кратной 2π, и колебания, возбуждаемые в точке Р обеими волнами, будут происходить в фазе. Следовательно, (4.1.93) является условием интерференционного максимума.

Если Δ равна полуцелому числу длин волн в вакууме:

(4.1.94)

то разность фаз оказывается равной δ = ±(2m + 1)π, и колебания, возбуждаемые в точке Р обеими волнами, будут происходить в противофазе. Следовательно, (4.1.94) является условием интерференционного минимума.

4.1.9. Дифракция световых волн

Дифракцией называется совокупность явлений, связанных с отклонениями от законов геометрической оптики. В частности, вследствие дифракции происходит огибание световыми волнами препятствий и проникновение света в область геометрической тени.

Между интерференцией и дифракцией нет существенного физического различия.

Свет, идущий от небольшого яркого источника через круглое отверстие (Рис. 4.1.11) должен по правилам геометрической оптики дать на экране резко ограниченный светлый кружок на темном фоне.

Рис. 4.1.11. Дифракция от круглого отверстия

Такая картина наблюдается при обычных условиях опыта. Но если расстояние от отверстия до экрана в несколько тысяч раз превосходит размеры отверстия, то образуется более сложная картина, которая состоит из совокупности светлых и темных концентрических колец.

Интересный случай дифракции осуществляется с помощью дифракционной решетки, которая представляет собой пластинку, на поверхности которой чередуются узкие параллельные прозрачные и непрозрачные полоски. Сумму ширины прозрачной и непрозрачной полосок называют периодом решетки. Пусть на решетку падает монохроматический свет с длиной волны λ (Рис. 4.1.12). Фронт волны параллелен плоскости решетки.

Рис. 4.1.12. Дифракционная решетка

Для того, чтобы все пучки усиливали друг друга, необходимо, чтобы разность хода равнялась целому числу длин волн:

(4.1.95)

Это условие позволяет определить те значения углов φ и соответствующие направления, в которых будут наблюдаться максимумы света длины волны λ.

Если на решетку падает белый свет, то в плоскости экрана получается ряд цветных изображений щели. На месте нулевого максимума будет изображение щели в белом свете, а по обе стороны от него развернутся цветные полосы от фиолетового к красному концу.

Чем больше общий размер решетки, т.е. чем больше полосок она содержит, тем выше ее качество: увеличение числа полосок увеличивает количество пропускаемого решеткой света (максимумы становятся ярче), и улучшает разрешение близких волн (максимумы становятся резче).

Зная период дифракционной решетки, ее можно использовать для определения длины световой волны, измерив величину угла φ, определяющего положение максимума данного порядка. В этом случае имеем:

(4.1.96)

Измерение длины световой волны с помощью дифракционной решетки принадлежит к числу наиболее точных методов.

4.1.10. Поляризация световых волн

Поляризованным называется свет, в котором направления колебаний электрического и магнитного векторов упорядочены каким-либо образом. В естественном свете колебания происходят в различных направлениях, быстро и беспорядочно сменяя друг друга.

Рис. 4.1.13. Структура плоскополяризованной световой волны

Рис. 4.1.14. Прохождение плоскополяризованного света через поляризатор

Следовательно, интенсивность прошедшего света определяется выражением:

(4.1.97)

Это соотношение носит название закона Малюса.

Пусть на пути естественного луча стоят два поляризатора, плоскости пропускания которых составляют угол φ. Из первого поляризатора выйдет плоскополяризованный свет, интенсивность которого I0 составит половину интенсивности естественного неполяризованного света I_ест. Используя закон Малюса, получаем:

(4.1.98)

4.1.11. Вращение плоскости
поляризации световых волн

Некоторые вещества, называемые оптически активными, обладают способностью вызывать вращение плоскости поляризации проходящего через них плоскополяризованного света. К числу таких веществ относятся кристаллы кварц, киноварь и др, некоторые жидкости (скипидар, никотин), растворы оптически активных веществ в оптически неактивных растворителях (водные растворы сахара, винной кислоты и др.)

Угол поворота плоскости поляризации в твердых веществах пропорционален пути l, пройденному лучом в кристалле:

(4.1.99)

В растворах угол поворота плоскости поляризации пропорционален пути l, пройденному светом в растворе и концентрации с активного вещества:

(4.1.100)

В зависимости от направления вращения вещества подразделяются на право- и левовращающие. Существуют правый и левый кварц, правый и левый сахар и т.д. Молекулы или кристаллы одной модификации являются зеркальным отражением молекул или кристаллов другой модификации.

Если между двумя скрещенными поляризаторами поместить оптически активное вещество, то поле зрения просветляется. Чтобы снова затемнить его, надо повернуть один из поляризаторов на угол, определяемый соотношениями (4.1.99) или (4.11.100). Таким методом можно измерить концентрацию активного вещества в растворе, в частности, концентрацию сахара.

© ФГОУ ВПО Красноярский государственный аграрный университет, 2015

Источник