второй закон термодинамики в дифференциальной форме

Второй закон термодинамики

Второй закон термодинамики. Энтропия. Вычисление изменения энтропии для различных процессов. Постулат Планка. Энергия Гиббса и энергия Гельмгольца. Уравнение Гиббса-Гельмгольца. Самопроизвольное протекание химических реакций. Расчет изменения энергии Гиббса в химических реакциях. Химический потенциал. Активность и летучесть.

Первый закон термодинамики не дает критериев направления самопроизвольных и несамопроизвольных процессов и условий, при которых наступает состояние равновесия. Лишь с появлением в термодинамике понятия энтропия появляется строгий критерий направления самопроизвольных процессов. Термин энтропия, как и второй закон термодинамики, были введены Клаузиусом в середине ХIХ века. Карно показал, что в тепловых машинахтеплота, полученная от источника тепла, не может быть полностью переведена в механическую работу, а часть ее должна быть передана третьему телу – холодильнику. Это обобщение по существу выражает второй закон термодинамики и может рассматриваться как одна из формулировок второго закона термодинамики. Рассмотрим также некоторые другие формулировки второго закона:

Формулировка Клаузиуса (1850 г.). Не возможен самопроизвольный процесс передачи теплоты от холодного тела к горячему.

Формулировка Кельвина (Томсона) (1851 г.). Не возможно превратить теплоту какого-либо тела в работу, не производя никакого другого действия, кроме охлаждения этого тела;

Формулировка по Оствальду. Вечный двигатель второго рода невозможен (т.е. не существует машины, которая бы полностью превращала теплоту в работу).

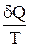
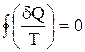
Клаузиус, рассматривая обратимый циклический процесс, состоящий из двух изотерм и двух адиабат (см. учебники), разбил его на бесконечно малые участки, просуммировал (учитывая знаки dQ) все величины (элементарная приведенная теплота), и показал, что для обратимого процесса

.

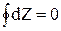
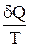
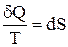
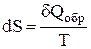
Если вспомнить свойства функции состояния, то для какой-то функции состояния Z интеграл , поэтому величина связана с какой-то функцией состояния. Эту функцию состояния назвали энтропией (S).

или , (1)

Выражение 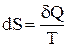(равенство Клаузиуса) – это дифференциальная форма записи второго закона термодинамики для обратимых процессов. Для необратимых процессов, как показал Клаузиус, справедливо неравенство

dS >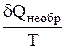, (2)

это дифференциальная форма записи второго закона термодинамики для необратимых процессов. В общем виде дифференциальная форма записи второго закона термодинамики для обратимых и необратимых процессов может быть представлена в виде:

dS 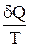, (3)

Энтропия – экстенсивная величина, т.е. пропорциональна массе системы.

Из дифференциальной формы записи второго закона термодинамики легко можно получить интегральную форму записи этого закона:

; (4)

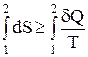
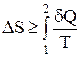
Первый и второй законы термодинамики можно объединить в так называемый объединенный первый и второй закон термодинамики, который для обратимых процессов можно записать следующим образом:

ТdS = dU + dA¢ + pdV. (5)

Если работа производится системой только против внешнего давления, то dA¢ = 0 и получаем:

Отсюда вытекает, что:

, (7)

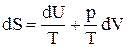
т.е. энтропия S является функцией внутренней энергии U и объема V: S = f(U,V).

В общем виде объединенный первый и второй закон термодинамики можно записать следующим образом:

ТdS 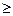dU + dA¢ + pdV (8)

Если рассматривать только объемную работу, то получим:

TdS 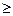dU + pdV (9)

Второй закон термодинамики для изолированных систем.

Для изолированной системы dQ = 0, m = const, U = const, V = const. Для необратимых процессов, протекающих в такой системе, можно записать, что

Выражения dS > 0 и DS > 0 можно рассматривать как математическую запись второго закона термодинамики, который для изолированной системы формулируется следующим образом:

в изолированной системе любой самопроизвольный процесс протекает только с увеличением энтропии, причем процесс закончится тогда, когда энтропия S достигнет своего максимального значения (когда наступит состояние равновесия).

При равновесии S₂ = S_max = const и DS = 0. Схематически все сказанное можно изобразить на графике зависимости S от пути процесса:

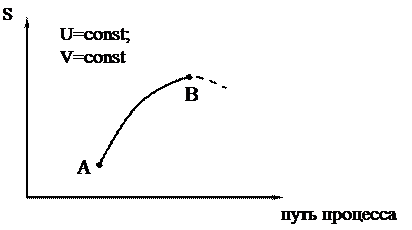Путь процесса – это какая-либо величина, которая меняется при протекании процесса и поддается опытному определению.

Участок АВ – необратимый самопроизвольный процесс (DS > 0), энтропия возрастает; участок ВA – необратимый нeсамопроизвольный процесс (DS

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Второй закон термодинамики. Необратимые процессы.

Необратимый процесс.

Необратимым называется физический процесс, который может самопроизвольно протекать только в одном определенном направлении.

В обратном направлении такие процессы могут протекать только как одно из звеньев более сложного процесса.

Необратимыми являются практически все процессы, происходящие в природе. Это связано с тем, что в любом реальном процессе часть энергии рассеивается за счет излучения, трения и т. д. Например, тепло, как известно, всегда переходит от более горячего тела к более холодному — это наиболее типичный пример необратимого процесса (хотя обратный переход не противоречит закону сохранения энергии).

Также висящий на легкой нити шарик (маятник) никогда самопроизвольно не увеличит ам­плитуду своих колебаний, наоборот, приведенный однажды в движение посторонней силой, он обязательно, в конце концов, остановится в результате сопротивления воздуха и трения нити о подвес. Таким образом, сообщенная маятнику механическая энергия переходит во внутреннюю энергию хаотического движения молекул (воздуха, материала подвеса).

Математически необратимость механических процессов выражается в том, что уравнение движения макроскопических тел изменяется с изменением знака времени: они не инвариантны при замене t на —t. При этом ускорение и силы, зависящие от расстояний, не изменяют свои знаки. Знак при замене t на —t меняется у скорости . Соответственно знак меняет сила, зависящая от скорости, — сила трения. Именно поэтому при совершении работы силами трения кинетическая энергия тела необратимо переходит во внутреннюю.

Направленность процессов в природе указывает второй закон термодинамики.

Второй закон термодинамики.

Второй закон термодинамики — один из основных законов термодинамики, устанавливающий необратимость реальных термодинамических процессов.

Второй закон термодинамики был сформулирован как закон природы Н. Л. С. Карно в 1824 г., затем У. Томсоном (Кельвином) в 1841 г. и Р. Клаузиусом в 1850 г. Формулировки закона различны, но эквивалентны.

Немецкий ученый Р. Клаузиус формулировал закон так: невозможно перевести теплоту от более холодной системы к более горячей при отсутствии других одновременных изменений в обеих системах или окружающих телах. Это означает, что теплота не может самопроизвольно пере­ходить от более холодного тела к более горячему (принцип Клаузиуса).

Согласно формулировке Томсона процесс, при котором работа переходит в тепло без каких-либо иных изменений состояния системы, необратим, т. е. невозможно преобразовать в работу все тепло, взятое от тела, не производя никаких других изменений состояния системы (принцип Томсона).

Источник

Физическая химия: конспект лекций.

5. Процессы. Второй закон термодинамики.

Второй закон термодинамики, в отличие от первого закона термодинамики, изучает все процессы, которые протекают в природе, и эти процессы можно классифицировать следующим образом.

Процессы бывают самопроизвольные, несамопроизвольные, равновесные, неравновесные.

Самопроизвольные процессы делятся на обратимые и необратимые. Второй закон термодинамики называют законом направленности процесса в изолированной системе (закон роста S). Слово «энтропия» создано в 1865 г. Р. Ю. Э. Клаузиусом – «тропе» с греческого означает превращение. В 1909 г. профессор П. Ауербах назвал царицей всех функций внутреннюю энергию, а S – тенью этой царицы. Энтропия – мера неупорядоченности системы.

Обратимые и необратимые процессы.

Необратимые процессы идут без затраты работы, протекают самопроизвольно лишь в одном направлении, это такие изменения состояния в изолированной системе, когда при обращении процессов свойства всей системы меняются. К ним относятся:

1) теплопроводность при конечной разности температур;

2) расширение газа при конечной разности давлений;

3) диффузия при конечной разности концентраций.

Обратимыми процессами в изолированной системе называются такие процессы, которые можно обратить без каких-либо изменений в свойствах этой системы.

Обратимые: механические процессы в системе, где отсутствует трение (идеальная жидкость, ее движение, незатухающие колебания маятника в вакууме, незатухающие электромагнитные колебания и распространение электромагнитных волн там, где нет поглощения), которые могут возвратиться в начальное состояние.

Самопроизвольные – процессы, которые идут сами собой, на них не затрачивается работа, они сами могут производить ее (движение камней в горах, Nа с большой скоростью движется по поверхности, так как идет выделение водорода проверить.).

Несамопроизвольные – процессы, которые не могут идти сами собой, на них затрачивается работа.

Равновесие делится на устойчивое, неустойчивое и безразличное.

Постулаты второго закона термодинамики.

1. Постулат Клаузиуса – не может быть перехода тепла от менее нагретого к более нагретому телу.

2. Постулат Томсона – теплота наиболее холодного тела не может служить источником работы.

Теорема Карно – Клаузиуса: все обратимые машины, совершающие цикл Карно с участием одного и того же нагревателя и одного и того же холодильника, имеют одинаковый коэффициент полезного действия, независимо от рода рабочего тела.

Аналитические выражения второго закона термодинамики.

1. Классическое уравнение второго закона термодинамики.

Q₂ / Т₂ – приведенное тепло холодильника;

Q₁ /Т₁= Q₂ /Т₂ – равенство приведенных теплот нагревателя и холодильника. Это второе уравнение термодинамики.

Если делим адиабатами на множество циклов Карно, то получим.

Это третье уравнение второго закона термодинамики для бесконечно малого цикла Карно.

Если процесс является конечным, то.

Это четвертое уравнение второго закона термодинамики Если процесс является замкнутым, то.

Это пятое уравнение второго закона термодинамики для обратимого процесса.

Интеграл по замкнутому контуру – интеграл Клаузиуса.

При необратимом процессе:

Это шестое уравнение второго закона термодинамики, или уравнение Клаузиуса, для обратимого процесса равно нулю, для необратимого процесса оно меньше 0, но иногда может быть больше 0.

Это седьмое уравнение второго закона термодинамики. Второй закон термодинамики – закон роста S.

Действие, обратное логарифму – потенцирование:

Первый закон термодинамики определяется постоянством функции U в изолированной системе. Найдем функцию, выражающую содержание второго закона, а именно, одностороннюю направленность протекающих в изолированной системе процессов. Изменение искомой функции должно иметь для всех реальных, т. е. необратимых процессов, протекающих в изолированных системах, один и тот же знак. Второй закон термодинамики в приложении к некруговым необратимым процессам должен выражатся неравенством. Вспомним Цикл Карно. Так как любой цикл можно заменить бесконечно большим числом бесконечно малых циклов Карно, то выражение:

Справедливо для любого обратимого цикла. Считая на каждом элементарном участке теплообмена Т = соnst, найдем, что:

Энергия Гельмгольца Изохорно-изотермический потенциал.

Величина (V – ТS) является свойством системы; она называется энергией Гельмгольца. Была введена Гельмгольцем в 1882 г.

F – полный дифференциал.

Увеличение объема приводит к тому, что изохорно-изотермический потенциал уменьшается (тот «минус», который стоит перед Р ). Повышение температуры приводит к тому, что F уменьшается.

Физический смысл изохорно-изотермического потенциала.

Убыль изохорно-изотермического потенциала равна максимальной работе, производимой системой в этом процессе; F – критерий направленности самопроизвольного процесса в изолированной системе. Для самопроизвольного процесса: АF_{Т г} 0. Для равновесного процесса: ΔF_Т,V = 0.

Изохорно-изотермический потенциал в самопроизвольных процессах уменьшается и, когда он достигает своего минимального значения, то наступает состояние равновесия (рис. 4).

Где 1 – самопроизвольный процесс;

2 – несамопроизвольный процесс;

3 – равновесный процесс.

Изобарно-изотермический потенциал.

1) G (Р, Т= соnst), энергия Гиббса.

G = U – ТS + РV = Н – ТS = F + РV,

Работа изобарно-изотермического процесса равна убыли изобарно-изотермического потенциала – физический смысл этой функции;

2) функция – полный дифференциал, однозначна, конечна, непрерывна.

dG = dU – ТdS – SdТ + рdv + vdр,

dG = ТdS – рdV – ТdS – SdТ + рdv + vdр,

Повышение температуры приводит к тому, что изобарно-изотермический потенциал уменьшается, так как перед S стоит знак «минус». Повышение давления приводит к тому, что изобарно-изотермический потенциал увеличивается, так как перед V стоит знак «плюс»;

3) G как критерий направленности процесса в изолированной системе.

Для самопроизвольного процесса: (ΔG)_Р,Т 0. Для равновесного процесса: (ΔG)_Р,Т = 0.

Изобарно-изотермический потенциал в самопроизвольных процессах уменьшается, и, когда он достигает своего минимума, то наступает состояние равновесия.

Где 1 – самопроизвольный процесс;

2 – равновесный процесс;

3 – несамопроизвольный процесс.

Совершается работа за счет ΔU и ΔН.

Противодействующие факторы. Энтальпийный фактор характеризует силу притяжения молекул. Энтропийный фактор характеризует стремление к разъединению молекул.

Энтальпия – Н Внутренняя энергия – U.

dU = ТdS – SdТ + рdV + Vdр,

dН = –рdV + рdV + Vdр; U = ТdS + VdР.

Где 1 – самопроизвольный процесс,

2 – несамопроизвольный процесс,

3 – равновесный процесс,

Уравнения Гиббса – Гельмгольца – уравнения максимальной работы.

Они позволяют установить связь между максимальной работой равновесного процесса и теплотой неравновесного процесса.

Уравнение Гельмгольца (уравнение связывающее функции F и G с их температурными производными).

Уравнение Гиббса (уравнение связывающее функции F и G с их температурными производными).

Уравнения эти дают возможность рассчитать работу через температурный коэффициент функции Гельмгольца или через температурный коэффициент функции Гиббса.

Уравнение Клаузиуса-Клапейрона.

Оно позволяет применить второй закон термодинамики к фазовым переходам. Если рассчитать процессы, в которых совершается только работа расширения, то тогда изменение внутренней энергии.

Предположим, что 1 моль вещества переходит из первой фазы во вторую.

Нет условного равновесия,

Где dР/dТ – температурный коэффициент давления,

Где λ_фп – теплота фазового перехода.

Уравнение Клаузиуса-Клапейрона, дифференциальная форма уравнения.

Уравнение устанавливает взаимосвязь между теплотой фазового перехода, давлением, температурой и изменением молярного объема.

Эмпирическая форма уравнения Клаузиуса-Клапейрона.

Уравнение Клаузиуса-Клапейрона изучает фазовые переходы. Фазовые переходы могут быть I рода и II рода.

I рода – характеризуются равенством изобарных потенциалов и скачкообразными изменениями S и V.

II рода – характеризуются равенством изобарных потенциалов, равенством энтропий и равенством молярных объемов.

Алгебраическая сумма приведенных теплот для любого обратимого кругового процесса равна нулю.

Эта подынтегральная величина – дифференциал однозначной функции состояния. Эта новая функция была введена Клаузиусом в 1865 г. и названа энтропией – S (от греч. «превращение»).

Любая система в различном состоянии имеет вполне определенное и единственное значение энтропии, точно так же, как определенное и единственное значение Р, V, Ти других свойств.

Итак, энтропия выражается уравнением:

Где S – это функция состояний, изменение которой dSв обратимом изотермическом процессе перехода теплоты в количество Q равно приведенной теплоте процесса.

При независимых переменных U (внутренняя энергия) может обозначаться U_ВН и V (объем), или Р (давление) и Н(энтальпия). Энтропия является характеристической функцией. Характеристические функции – функции состояния системы, каждая из которых при использовании ее производных дает возможность выразить в явной форме другие термодинамические свойства системы. Напомним, в химической термодинамике их пять:

1) изобарно-изотермический потенциал (энергия Гиббса) при независимых переменных Т, Р и числе молей каждого из компонентов и.;

2) изохорно-изотермический потенциал (энергия Гельмгольца) при независимых переменных Т, V, n_i;

3) внутренняя энергия при независимых переменных: S, V, n_i;

4) энтальпия при независимых переменных: S, Р, п_i;

5) энтропия при независимых переменных Н, Р, n_i..

В изолированных системах (U и V= соnst) при необратимых процессах энтропия системы возрастает, dS > 0; при обратимых – не изменяется, dS = 0.

Связь энтропии с другими термодинамическими параметрами.

Для того, чтобы решить конкретную задачу, связанную с применением энтропии, надо установить зависимость между ней и другими термодинамическими параметрами. Уравнение dS = δQ/Т в сочетании с δQ = dU + РdV и δQ = dН – VdР дает уравнения:

Применительно к функциональной зависимости φ(Т, V, S) = 0, получим.

Теперь найдем зависимость энтропии от температуры из уравнений:

Вот эти зависимости:

Эти два уравнения являются практически наиболее важными частными случаями общего соотношения:

Пользуясь разными зависимостями, можно вывести другие уравнения, связывающие термодинамические параметры.

Самопроизвольные – процессы, которые идут сами собой, на них не затрачивается работа, они сами могут производить ее (движение камней в горах, натрий с большой скоростью движется по поверхности, так как идет выделение водорода), а калий буквально «прыгает» по воде.

Несамопроизвольные – процессы, которые не могут идти сами собой, на них затрачивается работа.

Равновесие делится на устойчивое, неустойчивое и безразличное.

Постулаты второго закона термодинамики.

1. Постулат Клаузиуса – «Не может быть перехода тепла от менее нагретого к более нагретому телу».

2. Постулат Томсона – «Теплота наиболее холодного тела не может служить источником работы».

Теорема Карно-Клаузиуса: «Все обратимые машины, совершающие цикл Карно с участием одного и того же нагревателя и одного и того же холодильника, имеют одинаковый коэффициент полезного действия, независимо от рода рабочего тела».

Аналитические выражения второго закона термодинамики.

1. Классическое уравнение второго закона термодинамики.

Где Q /Т – приведенное тепло;

Q₂ / Т₂ – приведенное тепло холодильника;

Q₁ /Т₁= Q₂ / Т₂ – равенство приведенных теплот нагревателя и холодильника. Это второе уравнение термодинамики.

Если делим адиабатами на множество циклов Карно, то получим.

Это третье уравнение второго закона термодинамики для бесконечно малого цикла Карно.

Если процесс является конечным, то.

Это четвертое уравнение второго закона термодинамики.

Если процесс является замкнутым, то.

Это пятое уравнение второго закона термодинамики для обратимого процесса.

Интеграл по замкнутому контуру – интеграл Клаузиуса.

При необратимом процессе:

Шестое уравнение второго закона термодинамики, или уравнение Клаузиуса, для обратимого процесса равно нулю, для необратимого процесса оно меньше 0, но иногда может быть больше 0.

Это седьмое уравнение второго закона термодинамики. Второй закон термодинамики – закон роста S.

Термодинамическая вероятность.

Это формула Больцмана,

Где S – энтропия – степень разупорядоченности системы;

к– постоянная Больцмана;

W – термодинамическая вероятность системы макросостояний.

Термодинамическая вероятность – число микросостояний данной системы, с помощью которых можно реализовать данное макросостояние системы (Р, Т, V).

Если W = 1, то S = 0, при температуре абсолютного нуля –273°С все виды движений прекращаются.

Термодинамическая вероятность – это число способов, которыми атомы и молекулы можно распределить в объеме.

Источник