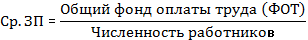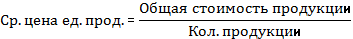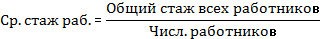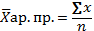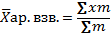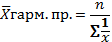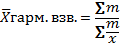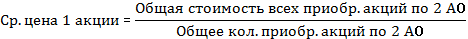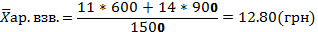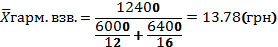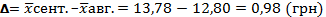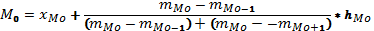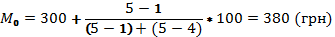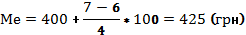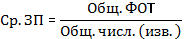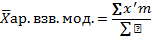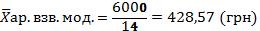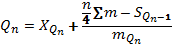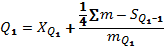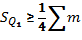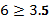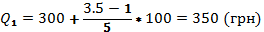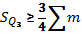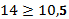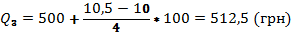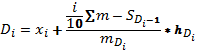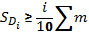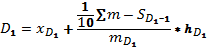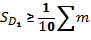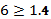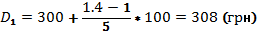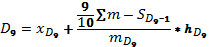выбор формы средней величины в статистике
8.3. Средние величины в статистике
Наиболее распространенной формой статистических показателей, используемой в экономических исследованиях, являются средние показатели (средняя величина).
Средняя величина – представляет обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени.
Показатель в форме средней величины выражает типичные черты и дает обобщающую характеристику однотипных явлений по одному из варьирующих признаков. Он отражает уровень этого признака, отнесенный к единице совокупности.
Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности.
Значения признака отдельных единиц совокупности колеблются в ту или иную сторону под влиянием множества факторов, среди которых могут быть как основные, так и случайные.
Сущность средней заключается, в том, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием факторов основных. Это позволяет средней отражать типичный уровень признака и абстрагироваться от индивидуальных особенностей, присущих отдельным единицам.
ВИДЫ СРЕДНИХ ВЕЛИЧИН наиболее часто применяемых на практике:
Выбор средней величины зависит от содержания осредняемого признака и конкретных данных, по которым ее приходится вычислять.
ФОРМУЛЫ СРЕДНИХ ВЕЛИЧИН
Таблица 8.2 – Результаты опроса работников офиса
Средние величины и показатели вариации
Понятие и виды средних величин
Существует 2 класса средних величин: степенные и структурные.
К структурным средним относятся мода и медиана, но наиболее часто применяются степенные средние различных видов.
Степенные средние величины
Степенные средние могут быть простыми и взвешенными.
Простая средняя величина рассчитывается при наличии двух и более несгруппированных статистических величин, расположенных в произвольном порядке по следующей общей формуле:
Взвешенная средняя величина рассчитывается по сгруппированным статистическим величинам с использованием следующей общей формулы:
Используя общие формулы простой и взвешенной средних при разных показателях степени m, получаем частные формулы каждого вида, которые будут далее подробно рассмотрены.
Средняя арифметическая
Например, студент сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5. Рассчитаем средний балл по формуле средней арифметической простой: (3+4+4+5)/4 = 16/4 = 4.
Средняя арифметическая взвешенная имеет следующий вид:
Например, студент сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5. Рассчитаем средний балл по формуле средней арифметической взвешенной: (3*1 + 4*2 + 5*1)/4 = 16/4 = 4.
Если значения X заданы в виде интервалов, то для расчетов используют середины интервалов X, которые определяются как полусумма верхней и нижней границ интервала. А если у интервала X отсутствует нижняя или верхняя граница (открытый интервал), то для ее нахождения применяют размах (разность между верхней и нижней границей) соседнего интервала X.
Средняя арифметическая применяется чаще всего, но бывают случаи, когда необходимо применение других видов средних величин. Рассмотрим такие случаи далее.
Средняя гармоническая
Средняя гармоническая применяется, когда исходные данные не содержат частот f по отдельным значениям X, а представлены как их произведение Xf. Обозначив Xf=w, выразим f=w/X, и, подставив эти обозначения в формулу средней арифметической взвешенной, получим формулу средней гармонической взвешенной:
Таким образом, средняя гармоническая взвешенная применяется тогда, когда неизвестны частоты f, а известно w=Xf. В тех случаях, когда все w=1, то есть индивидуальные значения X встречаются по 1 разу, применяется формула средней гармонической простой:
Средняя геометрическая
Средняя геометрическая применяется при определении средних относительных изменений, о чем сказано в теме Ряды динамики. Геометрическая средняя величина дает наиболее точный результат осреднения, если задача стоит в нахождении такого значения X, который был бы равноудален как от максимального, так и от минимального значения X.
Средняя квадратическая
Средняя квадратическая применяется в тех случая, когда исходные значения X могут быть как положительными, так и отрицательными, например при расчете средних отклонений.
Главной сферой применения квадратической средней является измерение вариации значений X, о чем пойдет речь позднее в этой лекции.
Средняя кубическая
Средняя кубическая применяется крайне редко, например, при расчете индексов нищеты населения для развивающихся стран (ИНН-1) и для развитых (ИНН-2), предложенных и рассчитываемых ООН.
Структурные средние величины
К наиболее часто используемым структурным средним относятся статистическая мода и статистическая медиана.
Статистическая мода
Если X задан дискретно, то мода определяется без вычисления как значение признака с наибольшей частотой. В статистической совокупности бывает 2 и более моды, тогда она считается бимодальной (если моды две) или мультимодальной (если мод более двух), и это свидетельствует о неоднородности совокупности.
Если X задан равными интервалами, то сначала определяется модальный интервал как интервал с наибольшей частотой f. Внутри этого интервала находят условное значение моды по формуле:
где Мо – мода;
ХНМо – нижняя граница модального интервала;
hМо – размах модального интервала (разность между его верхней и нижней границей);
fМо – частота модального интервала;
fМо-1 – частота интервала, предшествующего модальному;
fМо+1 – частота интервала, следующего за модальным.
Если размах интервалов h разный, то вместо частот f необходимо использовать плотности интервалов, рассчитываемые путем деления частот f на размах интервала h.
Статистическая медиана
Если X задан дискретно, то для определения медианы все значения нумеруются от 0 до N в порядке возрастания, тогда медиана при четном числе N будет лежать посередине между X c номерами 0,5N и (0,5N+1), а при нечетном числе N будет соответствовать значению X с номером 0,5(N+1).
Если X задан в виде равных интервалов, то сначала определяется медианный интервал (интервал, в котором заканчивается одна половина частот f и начинается другая половина), в котором находят условное значение медианы по формуле:
где Ме – медиана;
ХНМе – нижняя граница медианного интервала;
hМе – размах медианного интервала (разность между его верхней и нижней границей);
fМе – частота медианного интервала; 
Также как и в случае с модой, при определении медианы если размах интервалов h разный, то вместо частот f необходимо использовать плотности интервалов, рассчитываемые путем деления частот f на размах интервала h.
Показатели вариации
Размах вариации
Размах вариации – это разность между максимальным и минимальным значениями X из имеющихся в изучаемой статистической совокупности:
Недостатком показателя H является то, что он показывает только максимальное различие значений X и не может измерять силу вариации во всей совокупности.
Cреднее линейное отклонение
Например, студент сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5. Ранее уже была рассчитана средняя арифметическая = 4. Рассчитаем среднее линейное отклонение простое: Л = (|3-4|+|4-4|+|4-4|+|5-4|)/4 = 0,5.
Вернемся к примеру про студента, который сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5. Ранее уже была рассчитана средняя арифметическая = 4 и среднее линейное отклонение простое = 0,5. Рассчитаем среднее линейное отклонение взвешенное: Л = (|3-4|*1+|4-4|*2+|5-4|*1)/4 = 0,5.
Линейный коэффициент вариации
С помощью линейного коэффициента вариации можно сравнивать вариацию разных совокупностей, потому что в отличие от среднего линейного отклонения его значение не зависит от единиц измерения X.
В рассматриваемом примере про студента, который сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5, линейный коэффициент вариации составит 0,5/4 = 0,125 или 12,5%.
Дисперсия
В уже знакомом нам примере про студента, который сдал 4 экзамена и получил оценки: 3, 4, 4 и 5, ранее уже была рассчитана средняя арифметическая = 4. Тогда дисперсия простая Д = ((3-4) 2 +(4-4) 2 +(4-4) 2 +(5-4) 2 )/4 = 0,5.
В рассматриваемом примере про студента, который сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5, рассчитаем дисперсию взвешенную: Д = ((3-4) 2 *1+(4-4) 2 *2+(5-4) 2 *1)/4 = 0,5.
Если преобразовать формулу дисперсии (раскрыть скобки в числителе, почленно разделить на знаменатель и привести подобные), то можно получить еще одну формулу для ее расчета как разность средней квадратов и квадрата средней:
В уже знакомом нам примере про студента, который сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5, рассчитаем дисперсию методом разности средней квадратов и квадрата средней:
Д = (3 2 *1+4 2 *2+5 2 *1)/4-4 2 = 16,5-16 = 0,5.

Cреднее квадратическое отклонение
Выше уже было рассказано о формуле средней квадратической, которая применяется для оценки вариации путем расчета среднего квадратического отклонения, обозначаемое малой греческой буквой сигма:
Еще проще можно найти среднее квадратическое отклонение, если предварительно рассчитана дисперсия, как корень квадратный из нее:
В примере про студента, в котором выше рассчитали дисперсию, найдем среднее квадратическое отклонение как корень квадратный из нее:
.
Квадратический коэффициент вариации
В примере про студента, в котором выше рассчитали среднее квадратическое отклонение, найдем квадратический коэффициент вариации V = 0,707/4 = 0,177, что меньше критериального значения 0,333, значит вариация слабая и равна 17,7%.
Структурные средние



Понятие средней величины (СВ). Способы расчета средней.
Показатели вариации.
Структурные средние.
Понятие средней величины (СВ). Способы расчета средней.
Каждая однородная статистическая совокупность состоит из массы отдельных единиц, кот. обладают индивидуальными особенностями и поэтому отличаются друг от друга по размеру кол-ного признака.
Для получения обобщающей хар-ки большого кол-тва индивид. значений варьирующего признака рассчитываются средние величины.
Следует отметить, что к средней величине обращаются не только тогда, когда речь идёт о вариации признака, но и когда необходимо дать обобщающую инф-цию по всей совокупности.
Под средней величиной понимают обобщающий показатель, хар-щий типичный уровень или размер варьирующего признака в расчете на единицу однородной совокупности в конкретных условиях места и времени.
Таким образом средняя величина – это величина, кот. одним значением хар-ет нечто общее для совокупности в целом.
Средняя величина в статистике:
1) хар-ет типичный уровень варьирующего признака;
2) отражает то общее, что хар-но для всех единиц совокупности;
3) взаимопогашает различия, кот. наблюдаются у отдельных единиц совокупности.
Средние величины могут быть исчислены по непосредственному перечню значений варьирующего признака у каждой единицы совокупности.
Т.е. средняя величина может быть рассчитана по первичным несгруппированным данным и по сгруппированным данным. Такие средние назыв. простыми и взвешенными.
Если средние вычисляются по варьирующему ряду сгруппированной инф-ции с учетом статистического веса каждого варианта, то их назыв. взвешенными средними.
Способы расчета средней зависят:
1) от того какой инф-цией мы обладаем для расчета средней;
2) от хар-ра осреднённой величины.
Исходной базой расчета и критерием правильности выбора формы средней величины явл. исходное соотношение средней или смысловая формула.
Смысловая формула – это словесное описание методологии расчета средней величины.
Общий вид смысловой формулы:
Для каждого среднего показателя используемого в соц.-экон. анализе можно составить только одну смысловую формулу для расчета среднего показателя.
Составим смысловую формулу для расчета средней ЗП.
Средняя цена ед. продукции:
Средний стаж 1-го работника:
Средний процент выполнения плана по выпуску про-ции:
Выбор формы и вида средней величины происходит след. образом:
1) если известен знаменатель смысловой формулы и неизвестен числитель, то используют среднюю арифметическую;
2) если известен числитель смысловой формулы и неизвестен знаменатель, то выбираем форму средней гармонической;
3) если исходная инф-ция несгруппирована, то используют простую среднюю;
4) если исходная инф-ция сгруппирована, то используют среднюю взвешенную.
В статистике применяются 2 наиболее распространённых вида средней величины: средняя арифметическая и средняя гармоническая. При этом каждый из этих видом может иметь 2 формы: простую или взвешенную.
Средняя арифметическая простая – это отношение суммы значений признака в отдельных единицах совокупности к числу единиц совокупности.
x – значение признака в каждой единицы совокупности
n – кол-тво единиц совокупности.
Средняя арифметическая взвешенная – это отношение общего размера значений признака во всех единицах сгруппированной совокупности к численности единиц во всех группах.
m – веса, т.е. число ед. совокупности в каждой отдельной группе или может быть удельный вес каждой отдельной группы.
Средняя гармоническая простая – это обратное значение средней из обратных значений варьирующего признака, т.е. вариантов.
Средняя гармоническая взвешенная – это обратное значение средней из обратных значений варьирующего признака во всех единицах сгруппированной совокупности.
Для наглядности нарисуем схему форм и видов средних величин:
По пр-ю, занимающемуся торговлей ценных бумаг, имеются данные о приобретении акций в 2-х акционерных обществах.
| АО | Август | Сентябрь | |
| Кол-тво приобр. акций, шт (m) | Цена 1 акции, грн (x) | Стоим-ть приобр. акций, грн (m) | Цена 1 акции, грн (x) |
| №1 | |||
| №2 | |||
| Итого | х | х |
Опр-ть среднюю цену одной приобретённой акции по 2-м акционерным обществам в августе и сентябре.
Как изменилась средняя цена акции в абсолютном и относительном выражении.
Т.к. инф-ция сгруппирована и в смысловой формуле известен знаменатель и неизвестен числитель будем использовать среднюю арифметическую взвешенную.
В августе по 2-м акционерным обществам акции скупали в среднем по цене 12,80 (грн) за единицу.
Т.к. в сентябре месяце в смысловой формуле известен числитель и неизвестен знаменатель, инф-ция сгруппирована, веса неравны, то будем использовать среднюю гармоническую взвешенную.
В сентябре по 2-м АО в среднем скупали по 13,78 грн за единицу.
Абсолютное значение изменения ед. акции:
Относительное значения изменения ед. акции:
В сентябре месяце по сравнению с августом средняя цена одной акции выросла на 0,98 грн или в 1,077 раза, т.е. на 7,7%
Модой в статистике назыв. наиболее часто встречающиеся значения признака либо варианта совокупности. В дискретном вариационном ряду мода – это вариант, обладающий наибольшей частотой.
Для опр-ния моды в интервальном вариационном ряду сначала отыскивается модальный интервал (т.е. интервал, обладающий наибольшей частотой), а в рядах с неравными интервалами – по наибольшей плотности распределения.
Формула моды для интервальных вариационных рядов с равными интервалами:
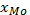
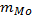

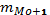
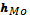
Медиана – это значение признака у той единицы совокупности, кот. делит упорядоченный, ранжированный вариационный ряд пополам, т.е. половина совокупности имеет значение меньше медианы, а другое – больше.
В дискретном вариационном ряду медиана – это интервал, кот. находится в центре ранжированного ряда.
Нахождение медианы в интервальном вариационном ряду требует предварительного нахождения медианного интервала.
Таким интервалом будет тот, накопленная (коммулитативная) частота кот. равна или превышает полу сумму частот ряда распределения.
После опр-ния медианного интервала, медиана вычисляется путём линейной интерпретации, т.е. по формуле:
– это нижняя граница;
– частота медианного интервала;

– ширина медианного интервала.
Имеются след. данные о распределении работников пр-я по уровню ЗП
| ЗП, грн | Числ. раб., чел. | S, чел | х’, грн (середина интервала) | x’m, грн. |
| 200-300 | ||||
| 300-400 | ||||
| (Ме) 400-500 | (mме) 4 | (Sме) 10 | ||
| 500-600 | ||||
| Итого | х | х |
Опр-ть моду и медиану.
На данном пр-и чаще всего встречаются работники с ЗП 380 грн.
Половина работников данного пр-я получают ЗП менее 425 грн, другая половина – больше.
Расчет средней величины в интервальном вариационном ряду распределения несколько отличается от расчета в дискретном вариационном ряду.
Для опр-ния средней величины в интервальном вариационном ряду распределения необходимо сначала найти середину ряда, таким образом перейдя от интервального вариационного ряда распределения к дискретному, потом расчет средней происходит обычным способом.
Обоснование формы и вида ср. величины.
Т.к. в смысловой формуле известен знаменатель, инф-ция сгруппирована, веса неравны, и мы осуществили переход от интервального вариационного ряда к дискретному, то будем использовать среднюю арифметическую взвешенную модифицированную.
Работники данного пр-я в среднем получают 428,57 грн.
Наряду с медианной для более полной хар-ки стр-ры изучаемой совокупности применяют и др. значения вариантов, занимающих в ранжированном ряду опр-ное положение. К ним относятся квартили и децили.
Квартили делят ряд по сумме частот на 4 равные части, а децили – на 10 частей.
Расчет этих показателей в вариационном ряду аналогичен расчету медианы и начинается с нахождения порядкового номера соотв. варианта и опр-ния по накопленной частоте того интервала, в кот. этот вариант находится. Затем с помощью линейной интерпретации, т.е. по формуле.
Квартиль находится по формуле:
Формула для децилей в интервальном вариационном ряду имеет след. вид:























 .
.