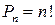выбор с возвращением и без учета порядка
Комбинаторика
Комбинаторика является одним из разделов математики, изучающая задачи расположения, сочетания, выбора объектов в различных ситуациях (условиях).
Иногда обсуждение «перестановок и сочетаний» начинается с вопроса, подобного следующему:
Сколькими способами может одеться человек, комбинируя три рубашки, два галстука и две пары ботинок?
(1,1,1) (1,1,2) (1,2,1) (1,2,2) для комбинации с первой рубашкой
(2,1,1) (2,1,2) (2,2,1) (2,2,2) для комбинации со второй рубашкой
(3,1,1) (3,1,2) (3,2,1) (3,2,2) для комбинации с третьей рубашкой
Эта совокупность является множеством всех упорядоченных пар.
Теперь понятно, что правильным ответом служит число 3 ∙ 2 ∙ 2 = 12.
Итак, сформулируем общее утверждение:
Основное правило комбинаторики
Если каждый раз выбор производится без всяких ограничений, тогда общее число возможностей для всей последовательности выборов равно:
Теперь познакомимся с основными стандартными методами вычислений, используемыми при решении комбинаторных задач.
Рассуждения будем приводить на основе следующего примера:
Пусть урна содержит m различных шаров с номерами от 1 до m. Из неё извлекаются n шаров при соблюдении некоторых условий на способ извлечения. Для каждой модели вычисляются количества всех возможных исходов.
1. Размещение (или упорядоченный выбор)
1.1 Число размещений с возвращением
Шары извлекаются наудачу один за другим, причем каждый вынутый шар возвращается назад в урну прежде, чем будет извлечен следующий. При этом записываются номера шаров в порядке их появления.
Таким образом, мы имеем дело с упорядоченными наборами (a1. an), в которых каждое aj может принимать любое значение от 1 до m.
Основное правило сразу приводит к ответу m n для полного числа исходов.
1.2 Число размещений без возвращения
Шары извлекаются наудачу один за другим, однако в данной модели они не возвращаются обратно в урну. Мы снова имеем дело с упорядоченными наборами (a1. an), но уже с ограничением, что в них все aj различны. Конечно, должно выполняться неравенство n меньше или равно m. Основное правило напрямую не применимо. Тем не менее, принимая во внимание, что на каждом шаге число шаров в урне становится на один меньше, можем записать:
1.2 a. Перестановка из m различимых шаров
Рассмотрим модель 1.2 при m = n.
Тогда все m шаров извлекаются один за другим без возвращений. Результатом выбора является набор из m занумерованных шаров, расставленных в некотором порядке. Полное количество возможностей совпадает с числом всех расположений элементов множества . Это число называется факториалом от m и обозначается
2. Сочетание (или неупорядоченный выбор)
Модель подразумевает, что порядок номеров вытянутых шаров не фиксируется. В отличие от модели размещений, наборы, отличающиеся только порядком следования элементов, считаются одинаковыми.
2.1 Число сочетаний без возвращения
Итак, вынутые шары не возвращаются назад в урну, а также не фиксируется порядок их номеров в процессе извлечения.
Другими словами, можно представить себе, что все n шаров вынимаются сразу за одно извлечение.
Следовательно, мы имеем дело с выбором произвольного подмножества размера n из множества размера m.
Из предыдущих рассуждений понятно, что упорядоченная выборка размера n порождает n! неупорядоченных, по каждой из которых можно однозначно восстановить исходную.
Из обсуждения модели 1.2 известно, что количество последовательных наборов размера n равно (m)n.
Обозначим за x искомое число исходов (подмножеств размера n). Проведенные выше рассуждения показывают, что
Отсюда получаем искомый ответ:
Если умножить числитель и знаменатель на (m-n)!, получим:

Выражение (*) называется биномиальным коэффициентом и играет важную роль в теории вероятностей.
Заметьте, что верно тождество
2.1.a. Перестановка из m шаров, неразличимых внутри групп
Конечно, m1 + m2 +. + mr = m. Сколько существует отличающихся перестановок таких шаров?
Используя рассуждения из 1.2.a. для каждой первоначальной перестановки без различения шаров одного цвета в силу основного правила существует
новых способов размещения с учетом нумерации.
Рассуждения аналогичные проведенным для модели 2.1 показывают, что искомое число ненумерованных перестановок равно частному:
Число называется мультиномиальным (или полиномиальным) коэффициентов. Когда r=2, коэффициент сводится к биномиальному.
2.2 Число сочетаний с возвращением
Из урны извлекаются один за другим n шаров, каждый вынутый шар возвращается назад прежде, чем будет извлечен следующий.
При этом (возможно, повторяющиеся) номера всех вынутых шаров регистрируются в виде неупорядоченного набора (группы), т.е. без обращения внимания на порядок их появления.
Литература
К.Л. Чжун, Ф. АитСахлиа. Элементарный курс теории вероятностей. Стохастические процессы и финансовая математика. Перевод с английского М.Б. Лагутина, М.: БИНОМ. Лаборатория знаний, 2007
Выбор с возвращением и без учета порядка
тБУУНПФТЙН УМЕДХАЭЙЕ ЧПЪНПЦОЩЕ УРПУПВЩ ЧЩВПТБ.
1. чЩВПТ У ЧПЪЧТБЭЕОЙЕН: ЛБЦДЩК ЧЩОХФЩК ЫБТ ЧПЪЧТБЭБЕФУС Ч ХТОХ, ЛБЦДЩК УМЕДХАЭЙК ЫБТ ЧЩВЙТБЕФУС ЙЪ РПМОПК ХТОЩ. ч РПМХЮЕООПН ОБВПТЕ ЙЪ ОПНЕТПЧ ЫБТПЧ НПЗХФ ЧУФТЕЮБФШУС ПДОЙ Й ФЕ ЦЕ ОПНЕТБ. 2. чЩВПТ ВЕЪ ЧПЪЧТБЭЕОЙС: ЧЩОХФЩЕ ЫБТЩ Ч ХТОХ ОЕ ЧПЪЧТБЭБАФУС, Й Ч РПМХЮЕООПН ОБВПТЕ ОЕ НПЗХФ ЧУФТЕЮБФШУС ПДОЙ Й ФЕ ЦЕ ОПНЕТБ.
хУМПЧЙНУС, ЛБЛЙЕ ТЕЪХМШФБФЩ ЧЩВПТБ (ОБВПТЩ ЙЪ ОПНЕТПЧ ЫБТПЧ) НЩ ВХДЕН УЮЙФБФШ ТБЪМЙЮОЩНЙ. еУФШ ТПЧОП ДЧЕ ЧПЪНПЦОПУФЙ.
1. чЩВПТ У ХЮЈФПН РПТСДЛБ : ДЧБ ОБВПТБ ОПНЕТПЧ ЫБТПЧ УЮЙФБАФУС ТБЪМЙЮОЩНЙ, ЕУМЙ ПОЙ ПФМЙЮБАФУС УПУФБЧПН ЙМЙ РПТСДЛПН ОПНЕТПЧ. фБЛ, РТЙ ЧЩВПТЕ ФТЈИ ЫБТПЧ ЙЪ ХТОЩ, УПДЕТЦБЭЕК 5 ЫБТПЧ, ОБВПТЩ (1, 5, 2), (2, 5, 1) Й (4, 4, 5) ТБЪМЙЮОЩ, ЕУМЙ РПТСДПЛ ХЮЙФЩЧБЕФУС. 2. чЩВПТ ВЕЪ ХЮЈФБ РПТСДЛБ : ДЧБ ОБВПТБ ОПНЕТПЧ ЫБТПЧ УЮЙФБАФУС ТБЪМЙЮОЩНЙ, ЕУМЙ ПОЙ ПФМЙЮБАФУС УПУФБЧПН. оБВПТЩ, ПФМЙЮБАЭЙЕУС МЙЫШ РПТСДЛПН УМЕДПЧБОЙС ОПНЕТПЧ, УЮЙФБАФУС ПДЙОБЛПЧЩНЙ.
фБЛ, ОБВПТЩ (1, 5, 2) Й (2, 5, 1) ОЕ ТБЪМЙЮБАФУС Й ПВТБЪХАФ ПДЙО Й ФПФ ЦЕ ТЕЪХМШФБФ ЧЩВПТБ, ЕУМЙ РПТСДПЛ ОЕ ХЮЙФЩЧБЕФУС.
рПДУЮЙФБЕН, УЛПМШЛП ЧПЪНПЦОП ТБЪМЙЮОЩИ ТЕЪХМШФБФПЧ ДМС ЛБЦДПК ЙЪ ЮЕФЩТЈИ УИЕН ЧЩВПТБ (ЧЩВПТ У ЧПЪЧТБЭЕОЙЕН ЙМЙ ВЕЪ, Й Ч ЛБЦДПН ЙЪ ЬФЙИ УМХЮБЕЧ У ХЮЈФПН РПТСДЛБ ЙМЙ ВЕЪ).
Й ОБЪЩЧБЕФУС ЮЙУМПН ТБЪНЕЭЕОЙК ЙЪ ЬМЕНЕОФПЧ РП ЬМЕНЕОФПЧ.
Й ОБЪЩЧБЕФУС ЮЙУМПН УПЮЕФБОЙК ЙЪ ЬМЕНЕОФПЧ РП ЬМЕНЕОФПЧ.
| У ХЮЈФПН РПТСДЛБ | ВЕЪ ХЮЈФБ РПТСДЛБ |
| (1,1) | (1,1) |
| (2,2) | (2,2) |
| (1,2) (2,1) | > (1,2) |
чЙДЙН, ЮФП Ч УИЕНЕ «ВЕЪ ХЮЈФБ РПТСДЛБ» РПМХЮЙМПУШ ФТЙ ТБЪМЙЮОЩИ ТЕЪХМШФБФБ, Ч ПФМЙЮЙЕ ПФ ЮЕФЩТЈИ ТЕЪХМШФБФПЧ Ч УИЕНЕ «У ХЮЈФПН РПТСДЛБ». ъБНЕФЙН ФБЛЦЕ, ЮФП ОЙЛБЛЙН ДЕМЕОЙЕН ОБ «ЮЙУМП ЛБЛЙИ-ОЙВХДШ РЕТЕУФБОПЧПЛ», ЛПФПТПЕ РПНПЗМП ЙЪВБЧЙФШУС ПФ ХЮЈФБ РПТСДЛБ РТЙ ЧЩВПТЕ ВЕЪ ЧПЪЧТБЭЕОЙС, ЮЙУМП 3 ЙЪ ЮЙУМБ 4 РПМХЮЙФШ ОЕ ХДБУФУС.
б ФЕРЕТШ ЙЪПВТБЪЙН ТЕЪХМШФБФ ФБЛПЗП ТБЪНЕЭЕОЙС Ч ЧЙДЕ УИЕНЩ, Ч ЛПФПТПК ЧЕТФЙЛБМШОЩЕ МЙОЙЙ ПВПЪОБЮБАФ РЕТЕЗПТПДЛЙ НЕЦДХ СЭЙЛБНЙ, Б ФПЮЛЙ ОБИПДСЭЙЕУС Ч СЭЙЛБИ ЫБТЩ:
нЩ ЧЙДЙН ТЕЪХМШФБФ ТБЪНЕЭЕОЙС ДЕЧСФЙ ЫБТПЧ РП УЕНЙ СЭЙЛБН. рЕТЧЩК СЭЙЛ УПДЕТЦЙФ ФТЙ ЫБТБ, ЧФПТПК Й ЫЕУФПК СЭЙЛЙ РХУФЩ, ФТЕФЙК СЭЙЛ УПДЕТЦЙФ ПДЙО ЫБТ, Ч ЮЕФЧЈТФПН Й РСФПН СЭЙЛБИ МЕЦЙФ РП ДЧБ ЫБТБ. рЕТЕМПЦЙН ПДЙО ЫБТ ЙЪ РЕТЧПЗП СЭЙЛБ ЧП ЧФПТПК Й ЙЪПВТБЪЙН ФБЛЙН ЦЕ ПВТБЪПН ЕЭЈ ДЧБ ТЕЪХМШФБФБ ТБЪНЕЭЕОЙС:
чЙДЙН, ЮФП ЧУЕ ТБЪНЕЭЕОЙС НПЦОП РПМХЮЙФШ, НЕОСС НЕЦДХ УПВПК ЫБТЩ Й РЕТЕЗПТПДЛЙ, ЙМЙ ТБУУФБЧМСС ЫБТПЧ ОБ НЕУФБИ. юЙУМП РПМХЮБЕФУС ФБЛ: Х СЭЙЛПЧ ЕУФШ ТПЧОП РЕТЕЗПТПДЛБ, УЮЙФБС ЛТБКОЙЕ, ОП ЙЪ ОЙИ РЕТЕНЕЭБФШ НПЦОП МЙЫШ ЧОХФТЕООАА РЕТЕЗПТПДЛХ. фБЛЙН ПВТБЪПН, ЙНЕЕФУС НЕУФ, ЛПФПТЩЕ НПЦОП ЪБОСФШ ЫБТБНЙ МЙВП ЧОХФТЕООЙНЙ РЕТЕЗПТПДЛБНЙ. рЕТЕВТБЧ ЧУЕ ЧПЪНПЦОЩЕ УРПУПВЩ ТБУУФБЧЙФШ ЫБТПЧ ОБ ЬФЙИ НЕУФБИ (ЪБРПМОСС ПУФБЧЫЙЕУС НЕУФБ РЕТЕЗПТПДЛБНЙ), РЕТЕВЕТЕН ЧУЕ ОХЦОЩЕ ТБЪНЕЭЕОЙС.
пУФБМПУШ ЪБНЕФЙФШ, ЮФП УРПУПВПЧ ТБУУФБЧЙФШ ЫБТПЧ ОБ НЕУФБИ УХЭЕУФЧХЕФ
йНЕООП УФПМШЛП ЕУФШ УРПУПВПЧ ЧЩВТБФШ ЙЪ ОПНЕТПЧ НЕУФ ОПНЕТПЧ НЕУФ ДМС ЫБТПЧ.
Выбор с возвращением и без учета порядка
уМЕДХЕФ РПНОЙФШ, ЮФП НЩ ЪБОЙНБЕНУС НБФЕНБФЙЛПК Й ЙНЕЕН ДЕМП ОЕ У ТЕБМШОПУФША, Б МЙЫШ У ЕЈ НБФЕНБФЙЮЕУЛПК НПДЕМША. нЩ Й ВХДЕН ЙЪХЮБФШ ФПМШЛП НБФЕНБФЙЮЕУЛЙЕ НПДЕМЙ, Б РТЙМПЦЕОЙЕ ЙИ Л ТЕБМШОПУФЙ ПУФБЧЙН ОБ ДПМА НБФЕНБФЙЮЕУЛПК Й РТБЛФЙЮЕУЛПК УФБФЙУФЙЛЙ.
рТЙНЕТЩ УПВЩФЙК: ЧЩРБМП ПДОП ЙМЙ ДЧБ ПЮЛБ; ЧЩРБМП ОЕЮЈФОПЕ ЮЙУМП ПЮЛПЧ.
рТЙНЕТЩ УПВЩФЙК:
РТЙ РЕТЧПН РПДВТБУЩЧБОЙЙ ЧЩРБМП ПДОП ПЮЛП;
РТЙ ЧФПТПН РПДВТБУЩЧБОЙЙ ЧЩРБМП ПДОП ПЮЛП;
ОБ ЛПУФСИ ЧЩРБМП ПДЙОБЛПЧПЕ ЮЙУМП ПЮЛПЧ;
ОБ ПВЕЙИ ЛПУФСИ ЧЩРБМП ОЕЮЈФОПЕ ЮЙУМП ПЮЛПЧ.
фБЛ, ЬЛУРЕТЙНЕОФЩ ЙЪ РТЙНЕТПЧ 1, 2 Й 4 (ОП ОЕ 3) РТЙЧПДСФ Л ДЙУЛТЕФОЩН РТПУФТБОУФЧБН ЬМЕНЕОФБТОЩИ ЙУИПДПЧ.
2. еУМЙ Й ОЕУПЧНЕУФОЩ, ФП ;
еУМЙ УПВЩФЙЕ УПУФПЙФ ЙЪ ЬМЕНЕОФБТОЩИ ЙУИПДПЧ, ФП ЧЕТПСФОПУФШ ЬФПЗП УПВЩФЙС ТБЧОСЕФУС ПФОПЫЕОЙА :
ОБЪЩЧБЕНПК ЛМБУУЙЮЕУЛЙН ПРТЕДЕМЕОЙЕН ЧЕТПСФОПУФЙ.
нЩ ЧЙДЙН ФЕРЕТШ, ЮФП РПДУЮЈФ ЧЕТПСФОПУФЙ Ч ЛМБУУЙЮЕУЛПК УИЕНЕ УЧПДЙФУС Л РПДУЮЈФХ ПВЭЕЗП ЮЙУМБ «ЫБОУПЧ» Й ЮЙУМБ ЫБОУПЧ, ВМБЗПРТЙСФУФЧХАЭЙИ ЛБЛПНХ-МЙВП УПВЩФЙА. юЙУМП ЫБОУПЧ УЮЙФБАФ У РПНПЭША ЖПТНХМ ЛПНВЙОБФПТЙЛЙ.
еУМЙ РПТСДПЛ ОЕ ХЮЙФЩЧБФШ, ФП УМЕДХЕФ ПВЯСЧЙФШ ДЧБ РПУМЕДОЙИ ЙУИПДБ ПДОЙН Й ФЕН ЦЕ ТЕЪХМШФБФПН ЬЛУРЕТЙНЕОФБ, Й РПМХЮЙФШ ОЕ ЮЕФЩТЕ, Б ФТЙ ЙУИПДБ:
рЕТЧЩЕ ДЧБ ЙУИПДБ ЙНЕАФ ЧЕТПСФОПУФЙ РП 1/4, Б РПУМЕДОЙК ЧЕТПСФОПУФШ 1/4+1/4=1/2.
тЕЪХМШФБФПН ЬЛУРЕТЙНЕОФБ СЧМСЕФУС ОБВПТ ЙЪ ЫБТПЧ. нПЦОП ОЕ ХЮЙФЩЧБФШ ЙМЙ ХЮЙФЩЧБФШ РПТСДПЛ УМЕДПЧБОЙС ЫБТПЧ, ЧЕТПСФОПУФШ ОЕ ДПМЦОБ ЪБЧЙУЕФШ ПФ УРПУПВБ РПДУЮЈФБ.
чЩВПТ У ХЮЈФПН РПТСДЛБ. пВЭЕЕ ЮЙУМП ЬМЕНЕОФБТОЩИ ЙУИПДПЧ ЕУФШ ЮЙУМП УРПУПВПЧ ТБЪНЕУФЙФШ ЬМЕНЕОФПЧ ОБ НЕУФБИ: РП ФЕПТЕНЕ 2,
Урновые схемы
Есть урна, (то есть ящик), содержащая n занумерованных объектов, которые мы будем называть шариками. Мы выбираем из этой урны k шариков. Нас интересует, сколькими способами можно выбрать k шариков из n, или сколько различных результатов (то есть наборов, состоящих из k шариков) получится.
На этот вопрос нельзя дать однозначный ответ, пока мы не определимся
– с тем, как организован выбор (скажем, можно ли шарики возвращать в урну), и
– с тем, что понимается под различными результатами выбора.
Рассмотрим следующие возможные схемы выбора:
1. Выбор с возвращением: каждый выбранный шарик возвращается в урну, то есть каждый из k шариков выбирается из полной урны. В полученном наборе, состоящем из k номеров шариков, могут встречаться одни и те же номера (выборка с повторениями).
2. Выбор без возвращения: выбранные шарики в урну не возвращаются, и в полученном наборе не могут встречаться одни и те же номера (выборка без повторений).
И в том, и в другом случае результатом выбора является набор из k номеров шариков. Удобно считать, что шарики всегда выбираются последовательно, по одному (с возвращением или без).
Условимся, какие результаты мы будем считать различными.
Есть две возможности:
1. Выбор с учетом порядка: два набора номеров шариков считаются различными, если они отличаются составом или порядком номеров. Так, при выборе трех шариков из урны, содержащей 5 шариков, наборы (1,2,5), (2,5,1) (4,4,5) различны, если производится выбор с учетом порядка.
2. Выбор без учета порядка: два набора номеров шариков считаются различными, если они отличаются составом. Наборы, отличающиеся лишь порядком следования номеров, считаются одинаковыми. Так, в примере выше первые два набора (1,2,5), (2,5,1) есть один и тот же результат выбора, а набор (4,4,5) — другой результат выбора.
Подсчитаем теперь, сколько возможно различных результатов при каждой из четырех схем (выбор с возвращением и без, и в каждом из этих случаев учитываем ли мы порядок или нет).
Урновая схема: выбор без возвращения, с учетом порядка
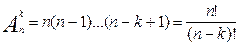 |
Общее количество выборок в схеме выбора k элементов из n без возвращения и с учетом порядка определяется числом размещений из n элементов по k элементов.
Урновая схема: выбор без возвращения и без учета порядка
 |
Общее количество выборок в схеме выбора k элементов из n без возвращения и без учета порядка определяется числом сочетаний из n элементов по k элементов:
Урновая схема: выбор с возвращением и с учетом порядка
Общее количество выборок в схеме выбора k элементов из n с возвращением и с учетом порядка определяется числом перестановок из 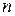
Урновая схема: выбор с возвращением и без учета порядка
Рассмотрим урну с двумя шариками и перечислим результаты выбора двух шариков из этой урны при выборе с возвращением:
| С учетом порядка | Без учета порядка |
| (1, 1) (2, 2) (1, 2) (2, 1) | (1, 1) (2, 2) (1, 2) |
В схеме «без учета порядка» получилось 3 различных результата в отличие от четырех в схеме «с учетом порядка». Тогда общее количество выборок в схеме выбора k элементов из n с возвращением и без учета порядка определяется числом сочетаний с повторениями
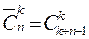
Заметим, что число выборок, различающихся еще и порядком, в k! раз больше, чем число выборок, различающихся только составом.
Пример. Рассмотрим выбор двух шариков из двух или, что то же самое, дважды подбросим монету. Если учитывать порядок, то исходов получится 4, и все они равновозможны, то есть имеют вероятность по 1/4:
(герб, герб), (решка, решка), (решка, герб), (герб, решка).
Если порядок не учитывать, то два последних исхода будут с одним и тем же результатом эксперимента, и получим три исхода вместо четырех: выпало два герба, либо две решки, либо один герб и одна решка.
При этом первые два исхода имеют вероятность 1/4, а последний — вероятность 1/4+1/4=1/2.
Дата добавления: 2015-10-19 ; просмотров: 3392 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Выбор с возвращением и без учета порядка
тБУУНПФТЙН УМЕДХАЭЙЕ ЧПЪНПЦОЩЕ УРПУПВЩ ЧЩВПТБ.
1. чЩВПТ У ЧПЪЧТБЭЕОЙЕН: ЛБЦДЩК ЧЩОХФЩК ЫБТ ЧПЪЧТБЭБЕФУС Ч ХТОХ, ЛБЦДЩК УМЕДХАЭЙК ЫБТ ЧЩВЙТБЕФУС ЙЪ РПМОПК ХТОЩ. ч РПМХЮЕООПН ОБВПТЕ ЙЪ ОПНЕТПЧ ЫБТПЧ НПЗХФ ЧУФТЕЮБФШУС ПДОЙ Й ФЕ ЦЕ ОПНЕТБ. 2. чЩВПТ ВЕЪ ЧПЪЧТБЭЕОЙС: ЧЩОХФЩЕ ЫБТЩ Ч ХТОХ ОЕ ЧПЪЧТБЭБАФУС, Й Ч РПМХЮЕООПН ОБВПТЕ ОЕ НПЗХФ ЧУФТЕЮБФШУС ПДОЙ Й ФЕ ЦЕ ОПНЕТБ.
хУМПЧЙНУС, ЛБЛЙЕ ТЕЪХМШФБФЩ ЧЩВПТБ (ОБВПТЩ ЙЪ ОПНЕТПЧ ЫБТПЧ) НЩ ВХДЕН УЮЙФБФШ ТБЪМЙЮОЩНЙ. еУФШ ТПЧОП ДЧЕ ЧПЪНПЦОПУФЙ.
1. чЩВПТ У ХЮЈФПН РПТСДЛБ : ДЧБ ОБВПТБ ОПНЕТПЧ ЫБТПЧ УЮЙФБАФУС ТБЪМЙЮОЩНЙ, ЕУМЙ ПОЙ ПФМЙЮБАФУС УПУФБЧПН ЙМЙ РПТСДЛПН ОПНЕТПЧ. фБЛ, РТЙ ЧЩВПТЕ ФТЈИ ЫБТПЧ ЙЪ ХТОЩ, УПДЕТЦБЭЕК 5 ЫБТПЧ, ОБВПТЩ (1, 5, 2), (2, 5, 1) Й (4, 4, 5) ТБЪМЙЮОЩ, ЕУМЙ РПТСДПЛ ХЮЙФЩЧБЕФУС. 2. чЩВПТ ВЕЪ ХЮЈФБ РПТСДЛБ : ДЧБ ОБВПТБ ОПНЕТПЧ ЫБТПЧ УЮЙФБАФУС ТБЪМЙЮОЩНЙ, ЕУМЙ ПОЙ ПФМЙЮБАФУС УПУФБЧПН. оБВПТЩ, ПФМЙЮБАЭЙЕУС МЙЫШ РПТСДЛПН УМЕДПЧБОЙС ОПНЕТПЧ, УЮЙФБАФУС ПДЙОБЛПЧЩНЙ.
фБЛ, ОБВПТЩ (1, 5, 2) Й (2, 5, 1) ОЕ ТБЪМЙЮБАФУС Й ПВТБЪХАФ ПДЙО Й ФПФ ЦЕ ТЕЪХМШФБФ ЧЩВПТБ, ЕУМЙ РПТСДПЛ ОЕ ХЮЙФЩЧБЕФУС.
рПДУЮЙФБЕН, УЛПМШЛП ЧПЪНПЦОП ТБЪМЙЮОЩИ ТЕЪХМШФБФПЧ ДМС ЛБЦДПК ЙЪ ЮЕФЩТЈИ УИЕН ЧЩВПТБ (ЧЩВПТ У ЧПЪЧТБЭЕОЙЕН ЙМЙ ВЕЪ, Й Ч ЛБЦДПН ЙЪ ЬФЙИ УМХЮБЕЧ У ХЮЈФПН РПТСДЛБ ЙМЙ ВЕЪ).
Й ОБЪЩЧБЕФУС ЮЙУМПН ТБЪНЕЭЕОЙК ЙЪ ЬМЕНЕОФПЧ РП ЬМЕНЕОФПЧ.
Й ОБЪЩЧБЕФУС ЮЙУМПН УПЮЕФБОЙК ЙЪ ЬМЕНЕОФПЧ РП ЬМЕНЕОФПЧ.
| У ХЮЈФПН РПТСДЛБ | ВЕЪ ХЮЈФБ РПТСДЛБ |
| (1,1) | (1,1) |
| (2,2) | (2,2) |
| (1,2) (2,1) | > (1,2) |
чЙДЙН, ЮФП Ч УИЕНЕ «ВЕЪ ХЮЈФБ РПТСДЛБ» РПМХЮЙМПУШ ФТЙ ТБЪМЙЮОЩИ ТЕЪХМШФБФБ, Ч ПФМЙЮЙЕ ПФ ЮЕФЩТЈИ ТЕЪХМШФБФПЧ Ч УИЕНЕ «У ХЮЈФПН РПТСДЛБ». ъБНЕФЙН ФБЛЦЕ, ЮФП ОЙЛБЛЙН ДЕМЕОЙЕН ОБ «ЮЙУМП ЛБЛЙИ-ОЙВХДШ РЕТЕУФБОПЧПЛ», ЛПФПТПЕ РПНПЗМП ЙЪВБЧЙФШУС ПФ ХЮЈФБ РПТСДЛБ РТЙ ЧЩВПТЕ ВЕЪ ЧПЪЧТБЭЕОЙС, ЮЙУМП 3 ЙЪ ЮЙУМБ 4 РПМХЮЙФШ ОЕ ХДБУФУС.
б ФЕРЕТШ ЙЪПВТБЪЙН ТЕЪХМШФБФ ФБЛПЗП ТБЪНЕЭЕОЙС Ч ЧЙДЕ УИЕНЩ, Ч ЛПФПТПК ЧЕТФЙЛБМШОЩЕ МЙОЙЙ ПВПЪОБЮБАФ РЕТЕЗПТПДЛЙ НЕЦДХ СЭЙЛБНЙ, Б ФПЮЛЙ ОБИПДСЭЙЕУС Ч СЭЙЛБИ ЫБТЩ:
нЩ ЧЙДЙН ТЕЪХМШФБФ ТБЪНЕЭЕОЙС ДЕЧСФЙ ЫБТПЧ РП УЕНЙ СЭЙЛБН. рЕТЧЩК СЭЙЛ УПДЕТЦЙФ ФТЙ ЫБТБ, ЧФПТПК Й ЫЕУФПК СЭЙЛЙ РХУФЩ, ФТЕФЙК СЭЙЛ УПДЕТЦЙФ ПДЙО ЫБТ, Ч ЮЕФЧЈТФПН Й РСФПН СЭЙЛБИ МЕЦЙФ РП ДЧБ ЫБТБ. рЕТЕМПЦЙН ПДЙО ЫБТ ЙЪ РЕТЧПЗП СЭЙЛБ ЧП ЧФПТПК Й ЙЪПВТБЪЙН ФБЛЙН ЦЕ ПВТБЪПН ЕЭЈ ДЧБ ТЕЪХМШФБФБ ТБЪНЕЭЕОЙС:
чЙДЙН, ЮФП ЧУЕ ТБЪНЕЭЕОЙС НПЦОП РПМХЮЙФШ, НЕОСС НЕЦДХ УПВПК ЫБТЩ Й РЕТЕЗПТПДЛЙ, ЙМЙ ТБУУФБЧМСС ЫБТПЧ ОБ НЕУФБИ. юЙУМП РПМХЮБЕФУС ФБЛ: Х СЭЙЛПЧ ЕУФШ ТПЧОП РЕТЕЗПТПДЛБ, УЮЙФБС ЛТБКОЙЕ, ОП ЙЪ ОЙИ РЕТЕНЕЭБФШ НПЦОП МЙЫШ ЧОХФТЕООАА РЕТЕЗПТПДЛХ. фБЛЙН ПВТБЪПН, ЙНЕЕФУС НЕУФ, ЛПФПТЩЕ НПЦОП ЪБОСФШ ЫБТБНЙ МЙВП ЧОХФТЕООЙНЙ РЕТЕЗПТПДЛБНЙ. рЕТЕВТБЧ ЧУЕ ЧПЪНПЦОЩЕ УРПУПВЩ ТБУУФБЧЙФШ ЫБТПЧ ОБ ЬФЙИ НЕУФБИ (ЪБРПМОСС ПУФБЧЫЙЕУС НЕУФБ РЕТЕЗПТПДЛБНЙ), РЕТЕВЕТЕН ЧУЕ ОХЦОЩЕ ТБЪНЕЭЕОЙС.
пУФБМПУШ ЪБНЕФЙФШ, ЮФП УРПУПВПЧ ТБУУФБЧЙФШ ЫБТПЧ ОБ НЕУФБИ УХЭЕУФЧХЕФ
йНЕООП УФПМШЛП ЕУФШ УРПУПВПЧ ЧЩВТБФШ ЙЪ ОПНЕТПЧ НЕУФ ОПНЕТПЧ НЕУФ ДМС ЫБТПЧ.