вычет в устранимой особой точке равен
Вычет в устранимой особой точке равен
> endstream endobj 14 0 obj 884 endobj 12 0 obj >> /Contents 13 0 R /CropBox [0 0 612 792] >> endobj 16 0 obj > stream GauHKbHBVY%,DFJs54t9Kd-2oJ>0jP49B&_]*ko;]-uB-2uW]4&ugYW9Q#_3M](4-;rf)NDm/>f 9re > XK8JK2ThKMOC _fD_J&q.. Uc
> endstream endobj 62 0 obj > stream Gar’$_.pkA%#44r$6@kgEOp54V.5TSgX351E+C7N1pTuK6f*94;Grmt`o@»_s-Cp+q/»\20]*MI V$+JE-T$N[OJ&AbF)h0Zk:sZ]FiVnL_C41l;kgPU5!W,!H)N\K=l=68MbcBc\Vh^&4M]q=dV@[b 0g9:s:/F8_K;2ak]%VD8,@u5a:5r2):Wl>’eT0O+0fYVr72!cG’ih556hR9U(W>a6?>«oj0+`L ^JF/$HS3SfR[E9n?B[`>e,C(:`(]:c#IiZ*ci=%G
> endstream endobj 67 0 obj > stream Gar’$_.pkA%#44r$6@kgEOp54V.5TSgX351E+C7N1pTuK6f*94;Grmt`o@»_s-Cp+q/»\20]*MI V$+JE-T$N[OJ&AbF)h0Zk:sZ]FiVnL_C41l;kgPU5!W,!H)N\K=l=68MbcBc\Vh^&4M]q=dV@[b 0g9:s:/F8_K;2ak]%VD8,@u5a:5r2):Wl>’eT0O+0fYVr72!cG’ih556hR9U(W>a6?>«oj0+`L ^JF/$HS3SfR[E9n?B[`>e,C(:`(]:c#IiZ*ci=%G
> endstream endobj 70 0 obj 273 endobj 2 0 obj > endobj 3 0 obj > endobj xref 0 71 0000000000 65535 f 0000000010 00000 n 0000166967 00000 n 0000167022 00000 n 0000001339 00000 n 0000000210 00000 n 0000001316 00000 n 0000040642 00000 n 0000086675 00000 n 0000002389 00000 n 0000001531 00000 n 0000002366 00000 n 0000003589 00000 n 0000002582 00000 n 0000003566 00000 n 0000005211 00000 n 0000003783 00000 n 0000005187 00000 n 0000012757 00000 n 0000005405 00000 n 0000012733 00000 n 0000015966 00000 n 0000012951 00000 n 0000015942 00000 n 0000018082 00000 n 0000016160 00000 n 0000018058 00000 n 0000021281 00000 n 0000018276 00000 n 0000021257 00000 n 0000022627 00000 n 0000021475 00000 n 0000022603 00000 n 0000024564 00000 n 0000022811 00000 n 0000024540 00000 n 0000027726 00000 n 0000024758 00000 n 0000027702 00000 n 0000031310 00000 n 0000027920 00000 n 0000031286 00000 n 0000034144 00000 n 0000031504 00000 n 0000034120 00000 n 0000037825 00000 n 0000034338 00000 n 0000037801 00000 n 0000040448 00000 n 0000038019 00000 n 0000040424 00000 n 0000040799 00000 n 0000085734 00000 n 0000041951 00000 n 0000042169 00000 n 0000086652 00000 n 0000086832 00000 n 0000140677 00000 n 0000088158 00000 n 0000088376 00000 n 0000141702 00000 n 0000141883 00000 n 0000153949 00000 n 0000142098 00000 n 0000142319 00000 n 0000154323 00000 n 0000154504 00000 n 0000166570 00000 n 0000154719 00000 n 0000154940 00000 n 0000166944 00000 n trailer > startxref 167190 %%EOF
Вычет в устранимой особой точке равен
Обозначается вычет
Вычет функции в конечной изолированной особой точке равен коэффициенту С-1 при первой отрицательной степени в разложении функции в ряд Лорана в окрестности этой точки, т.е. при 1/(z—z0) для z0, принадлежащей области комплексных чисел:
ПРИМЕР 1. Вычисление вычета функции в ее конечных особых точках.
Если конечная особая точка z0 является устранимой особой точкой функции f(z), то
ПРИМЕР 2. Вычисление вычета в устранимой особой точке.
ПРИМЕР 3. Вычисление вычета в полюсе порядка n.
ПРИМЕР 4. Вычисление вычета в простом полюсе.
ПРИМЕР 5. Вычисление вычета в существенной особой точке.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Какие налоговые вычеты можно получить в 2021 году
Кому положены и как подтвердить
С помощью налоговых вычетов можно ощутимо сэкономить и поправить семейный бюджет.
Уже можно подавать декларацию в налоговую инспекцию и возвращать налог, уплаченный за прошлый год. При этом многие люди имеют право сразу на несколько вычетов, но сложно разобраться, какие нужны документы и как все оформить.
В этой статье я сделала подборку основных типов вычетов: кому положены, в какой сумме и как их подтвердить.
О чем расскажу в статье:
Что такое вычеты
Почти все мы платим НДФЛ — с зарплаты и других доходов. Если вы потратились на лечение, учебу, купили квартиру или пополнили индивидуальный инвестиционный счет (ИИС), то имеете право на вычет — возврат части уплаченного НДФЛ. Вычет можно получить двумя способами:
Получить вычет могут только те, у кого есть официальный доход, с которого платится НДФЛ по ставке 13%. Еще нужно быть резидентом РФ — проживать в России не менее 183 дней в календарном году. В 2020 году можно было стать резидентом, если прожить в стране 90 дней. Для этого нужно подать заявление в инспекцию до 30 апреля 2021 года. Нерезиденты воспользоваться вычетом не могут.
Чем раньше подать декларацию по итогам года, тем быстрее вернут деньги из бюджета.
Срок подачи декларации — до 30 апреля следующего года. Это касается только тех, кто обязан задекларировать свои доходы: например, если человек сдавал в аренду имущество или продал квартиру, которая находилась в собственности менее минимального срока владения — трех или пяти лет в зависимости от ситуации.
А те, кто хочет просто воспользоваться налоговым вычетом, например вернуть 13% от сумм за обучение или лечение, могут подать декларацию в течение трех лет с того года, как оплатили расходы. А вычетом на покупку жилья можно воспользоваться и спустя три года, и через десять лет после покупки — ограничений по срокам для этого вычета нет.
Какие бывают типы вычетов
По доходам за 2020 год можно воспользоваться следующими видами вычетов:
По доходам, которые получили с 2021 года, можно будет также воспользоваться новыми видами вычетов. О них мы расскажем в отдельных статьях.
Как победить выгорание
Что изменилось в вычетах в 2021 году
26 января 2021 года первое чтение в Госдуме прошел законопроект, который упростит процедуру получения некоторых вычетов: воспользоваться вычетом можно будет «в один клик». Это новшество коснется, скорее всего, вычетов на лечение и обучение, имущественного вычета при покупке жилья, расходов на уплату процентов по ипотеке, а также инвестиционных вычетов по операциям на ИИС. Но пока этот закон не принят, продолжает действовать старый порядок.
До 2021 года применять вычеты можно было ко всем доходам, которые облагаются по ставке 13%, кроме дивидендов. С 2021 года доходы физлиц разделяются на налоговые базы — неосновную и основную:
К доходам из основной налоговой базы вычеты можно будет применять свободно, из неосновной — только три вычета:
Но эти новшества нужно будет учитывать при заявлении вычетов на расходы, которые были в 2021 году, то есть при подаче декларации в начале 2022 года. Пока же отчитываемся перед налоговой за 2020 год в старом порядке — только по тем доходам, которые облагаются по ставке 13%.
Имущественные налоговые вычеты
Имущественные вычеты может получить человек, который совершал операции с недвижимостью. В частности:
Полный перечень операций, по которым можно получить имущественный вычет, а также порядок их предоставления прописан в статье 220 НК РФ.
Рассмотрю вычеты, которые вызывают больше всего вопросов.
При покупке квартиры в новостройке или на вторичном рынке можно воспользоваться вычетом по расходам на приобретение жилья.
Если квартиру приобретать в ипотеку, то государство вернет еще больше: кроме вычета на жилье можно воспользоваться и вычетом на проценты.
Кому положены. Вычет может получить человек, который приобрел квартиру и заплатил за нее полностью или частично. От расходов будет зависеть сумма вычета. По квартирам, которые получены по наследству или подарены, получить вычет нельзя: за них приобретатель ничего не платил.
Получить вычет можно только после того, как оформлен правоустанавливающий документ на квартиру.
В случае новостройки — когда дом сдан и подписан акт приема-передачи.
На вторичном рынке — свидетельство о праве собственности или выписка из ЕГРН.
Если квартира приобретена в браке, то она считается совместной собственностью. Не важно, на кого оформлена квартира, кто за нее платил, — вычет могут получить оба супруга.
Если квартиру приобрели супруги, то вычеты могут быть распределены между ними по заявлению в любых пропорциях независимо от того, на кого оформлена квартира и кто за нее платил.
Кроме того, распределять вычет нужно, только если второй супруг тоже хочет получить вычет по этой квартире. Если такого желания второй супруг не изъявляет, то вычет получит только один супруг, без заявления о распределении вычета.
Неиспользованный остаток вычета на проценты нельзя переносить на другие объекты. Он дается только на один объект. То есть неиспользованный остаток вычета просто сгорит.
Вычет на проценты также можно распределять между супругами по их заявлению. При этом не важно, на кого оформлен кредитный договор и кто платит банку. В отличие от вычета на покупку квартиры, заявление можно писать каждый год и перераспределять проценты.
Проверьте, сколько вам вернут при покупке квартиры, в нашем калькуляторе:
Документы. Воспользоваться вычетом можно двумя способами:
Если квартира в новостройке, то в инспекцию необходимо представить такие документы:
Если квартира куплена на вторичном рынке, то подтвердить право на вычет можно такими документами:
Для получения вычета на проценты, уплаченные банку, представляются такие документы:
Если вычет заявляется супругами, то необходимо представить заявление о распределении вычета.
Нюансы, о которых мы писали в Т—Ж:
Если квартира находилась в собственности пять лет, а в определенных случаях — три года, при ее продаже не нужно платить налог и подавать декларацию.
Если продать квартиру раньше этого срока, то придется отчитаться перед налоговой инспекцией. Что касается налога, либо его можно уменьшить, либо его совсем может не быть — если воспользоваться имущественным вычетом.
Кому положены. Вычетом могут воспользоваться продавцы квартир. Им также можно воспользоваться при продаже долей, жилых домов, комнат, включая приватизированные жилые помещения, садовых домов или земельных участков или доли в этом имуществе.
При продаже квартиры, которая находится в общей долевой или совместной собственности, вычет в 1 000 000 Р распределяется между совладельцами квартиры пропорционально их доле. Либо это делается по договоренности между совладельцами долей, не выделенных в натуре.
Вычет на продажу квартиры, в отличие от вычета на покупку квартиры, можно применять неограниченное количество раз. То есть его можно использовать хоть каждый год.
Вычет в размере документально подтвержденных расходов на покупку квартиры. Когда все документы на руках, лучше применить этот вычет.
Чтобы посчитать, какой налог нужно заплатить при продаже квартиры, воспользуйтесь нашим калькулятором:
Документы. Для применения вычета 1 000 000 Р нужно подать в инспекцию декларацию и приложить к ней копию договора купли-продажи.
Если доход от продажи квартиры уменьшать на расходы, которые были при покупке этой квартиры, то дополнительно нужно представить копии документов по предыдущей сделке:
Стандартные налоговые вычеты
Кому положены. Стандартные налоговые вычеты делятся на две категории: вычеты на себя и на детей.
Вычеты на себя. Вычет предоставляется определенным категориям физлиц. Например, инвалидам с детства, инвалидам первой и второй групп, «чернобыльцам», родителям и супругам военнослужащих, погибших при исполнении военных обязанностей, и другим. Перечень лиц, которые могут претендовать на стандартный налоговый вычет, есть в законе.
Вычет на ребенка (на детей). Эти вычеты предоставляются обоим родителям. На вычет также могут претендовать усыновители, опекуны, попечители, приемные родители. Важно, чтобы ребенок находился на их обеспечении.
Вычет предоставляется с месяца, в котором родился ребенок, и до конца того года, в котором он достиг 18 или 24 лет, если продолжает учиться очно.
Электронная библиотека
Пусть функция w = f(z) – аналитическая в окрестности точки z0, за исключением самой точки (т.е. z0 – изолированная особая точка функции w = f(z)).
Вычет обозначается: или res f(z0) (происходит от слова resudi – остаток):
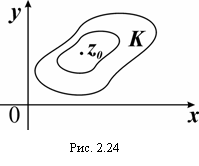
Теорема: Вычет относительно устранимой особой точки равен нулю.
Доказательство: Пусть z0 – устранимая точка, тогда функция
будет аналитическая в окрестности z0 и по теореме Коши что и требовалось доказать.
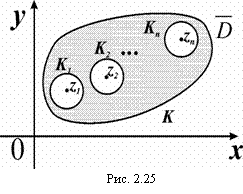
Доказательство: Опишем из каждой особой точки zК (k = 1, 2,…,n) как из центра, окружности Кк настолько малого радиуса, чтобы они целиком лежали в и не содержали других особых точек функции f(z) (рис. 2.25).
В многосвязной области f(z) будет аналитической. По теореме Коши:
Умножим и разделим правую часть последнего равенства на 2p I получим:
Что и требовалось доказать.
Найдем вычет относительно простого полюса. Пусть f(z) имеет в точке простой полюс, тогда
Как отмечено ранее она аналитическая в окрестности z0 и по формуле Коши
Вывод: вычет относительно простого полюса находят по формуле:
Найти вычет функции относительно точки z = 0.
Решение. Для функции точка z = 0 – простой полюс. Поэтому
Формула (2.88) получается сразу:
Решение. Согласно формуле (2.88)
так как z = 0 – простой полюс.
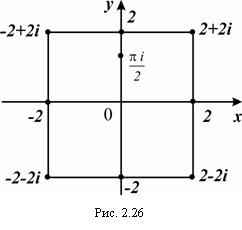
Решение. Функция имеет две особые точки z = 0 и z = 2; обе точки попадают в область, ограниченную окружностью |z| = 3.
Точка z = 0 – устранимая, так как
а вторая – простой полюс (сделайте рисунок).
Вычет относительно устраненной точки равен нулю. Вычет относительно точки z = 2 находим по формуле (2.88):
По основной теореме Коши о вычетах (2.85), получим:
Вывод формулы для нахождения вычета относительно кратного полюса аналогичен рассуждениям, проведенным для случая простого полюса, а именно: если f(z) имеет в точке z0 кратный полюс, то для функции (k – кратность полюса) точка z0 устранимая. Тогда функция
аналитическая в окрестностях z0. Значит,
Но на контуре поэтому
Вывод: получена формула для нахождения вычета функции относительно полюса порядка k:
Задачи для упражнений
Вычислить интегралы, используя основную теорему Коши о вычетах:
Вычеты. Основная теорема о вычетах
Содержание:
По этой ссылке вы найдёте полный курс лекций по математике:
] в лорановском разложении этой функции в точке z0. Отсюда, в частности, вытекает, что вычет в устранимой особой точке равен нулю. Укажем некоторые формулы для вычисления вычета в полюсе функции /(г).
Поэтому по теореме Коши для многосвязной области имеем Из этой формулы, пользуясь определением вычета получаем требуемое равенство (5). 6.1. Вычет функции относительно бесконечно удаленной точки Говорят, чтофункция f(z) является аналитической в бесконечно удаленной точке z = оо, если функция аналитична вточке С =0. Это следует понимать так: функцию g(0= f (f) можно доопределить до аналитической, положив Например, функция аналитична в точке z = оо, поскольку функция аналитична в точке С = 0.
Возможно вам будут полезны данные страницы:
Пусть функция /(г) аналитична в некоторой окрестности бесконечно удаленной точки (кроме самой точки z = оо). Точка z = оо называется изолированной особой точкой функции /(г), если в некоторой окрестности этой точки нет других особых точек функции f(z). Функция имеет в бесконечности неизолированную особенность: полюсы zk = к-к этой функции накапливаются в бесконечности, если к оо. Говорят, что z — оо является устранимой особой тонкой, полюсом или существенно особой точкой функции f(z) в зависимости от того, конечен, бесконечен или вовсе не существует lim f(z).
Критерии типа бесконечно удаленной точки, связанные с разложением Лорана, изменяюгся по сравнению с критериями для конечных особых точек. Теорема 22. Если z — оо является устранимой особой точкой функции /(z), то лоранов-ское разложение f(z) в окрестности этой точки не содержит полож и тельных степеней z;eaiu z — оо — полюс, то это разложение содержит конечное число положительных степеней z, в случае существенной особенности — бесконечное число положительных степеней z.
При этом лорановским разложением функции /(z) в окрестности бесконечно удаленной точки будем называть разложение в ряд Лорана, сходящийся всюду вне круга достаточно большого радиуса R с центром в точке z — 0 (кроме, быть может, самой точки z — оо). Пусть функция f(z) — аналитична в некоторой окрестности точки z = оо (кроме, быть может, самой этой точки). Вычетом функции /(z) в бесконечности называют величину пае 7 — достаточно большая окружность \z\ = р, проходимая по часовой стрелке (так, что окрестность точки z — оо остается слева, как и в случае конечной точки г = го).
И з этого определения следует, что вычет функции в бесконечности равен коэффициенту при z
Известные тейлоровские разложения функций е1, cosz, sinz, chz, shz можно рассматривать также и как лорановские разложения в окрестности точки z — оо.
Так как все эти разложения содержат бесконечное множество положительных степеней z, то перечисленные функции имеюгвточке z = оо существенную особенность. Теорема 23. Если функция f(z) имеет в расширенной комплексной плоскости конечное число особых точек, то сумма всех ее вычетов, включая и вычет в бесконечности, равна нулю. Так что, если — конечные особые точки функции f Вычислить интеграл Полюсами (конечными) подынтегральной функции являются корни zt уравнения гя = —1, которые все лежат внутри окружности В окрестности точки г = оо функция /(z) имеет следующее разложение: ИЗ КОТОРОГО ВИДНО, ЧТО В силу теоремы 6.2. Приложение вычетов к вычислению определенных интегралов. Интегралы от рациональных функций Теорема 24. Пусть f(x) — рациональная функция, т. е. где — многочлены степеней пит соответственно. Пример 6. Вычислить интеграл Применяя подстановку z = е,г. после простых преобразований (см. формулы (II)) получим, что Внутри единичного круга при условии находится только один полюс (второго порядка) Вычет функции Интегралы вида гдеД(х) — правильная рациональная дробь, а > 0 — вещественное число. При вычислении таких интегралов часто бывает полезной следующая лемма. Лемма Жордана. Пусть функция f(z) аналитична в верхней полуплоскости исключением конечного числа изолированных особых точек, и при \ стремится к нулю равномерно относительно arg z. где 7л — верхняя полуокружность Условие равномерного стремления /(г) к нулю означает, что на полуокружности 7R Оценим исследуемый интефал. Замечая, что на 7Л В силу известного неравенства (см. рис. 31) справедливого при (для доказательства достаточно заметить, что и, значит, функция ^ убывает на полуинтервале Сопоставляя формулы (13) и (14), заключаем, что 4 Введем вспомогательную функцию Пример 7. Вычислить интеграл Нетрудно видеть, что если г = х, то Jmh(z) совпадает с подынтегральной функцией. Отсюда откуда Упражнения Найдите действительную и мнимую части функдаи: Найдите образы действительной и мнимой осей при отображении: Докажи те, что функция непрерывна на всей комплексной плоскости: Пользуясь условиями Коши—Римана, выясните, является ли функция аналитической хотя бы в одной точке или нет: Восстановите аналитическую в окрестности точки 20 функцию /(г) по известной действительной части и (или по известной мнимой части v(x, у)) и значению f(z0): Покажите, что следующие функци и являются гармоническими: Может ли данная функция быть действительной или мнимой частью аналитической функции Найдите действительную и мнимую части функции: Найдите модуль и главное значение аргумента функции в указанной точке zq: Найдите логарифмы следующих чисел: Решите уравнение: 38. Вычислите интеграл /— линия, соединяющая точки z\ = 0 отрето к прямой, б) дуга параболы ломаная 39. Вычислите интеграл — полуокружность Вычислите интегралы: 43. Вычислите интеграл / где 7 — верхняя половина окру*« ости |z| = 1 (выбирается Вычеты Основная теорема о вычетах Применение вычетов к вычислению интегралов Вычет функции относительно бесконечно удаленной точки Приложение вычетов к вычислению определенных интегралов Интегралы от рациональных функций Лемма Жордана Вычисление интегралов Френеля ветвь функци и л/z, для которой 44. Вычислите интеграл / ^ dz, где 7 — отрезок прямой, идущий из точки zj = 1 в точку. Вычислите интегралы: Найдите радиус сходимости ряда: Рашожите функцию в ряд Тейлора и найдите радиус сходимости полученного ряда: постепеням z + I. 55. cosz постепеням 56.—-— постепеням z + 2. 57.—^— постепеням z. 58. sh2 z постепеням z. Найдите нули функции и определите их порядки: z Определите область сходимости ряда: Разложите в ряд Лорана в окрестности точки г = 0: Разяожитс в ряд Лорана в уюзан ном кольце: Найдите особые точки и определит е их характер: Присылайте задания в любое время дня и ночи в ➔ Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института. Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.Пример 4:
Пример 5:
Тогда для любого положитыьного а





















