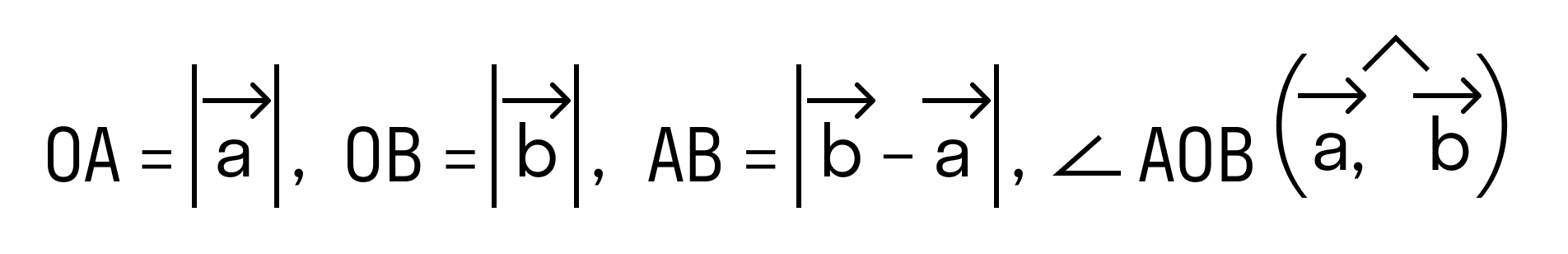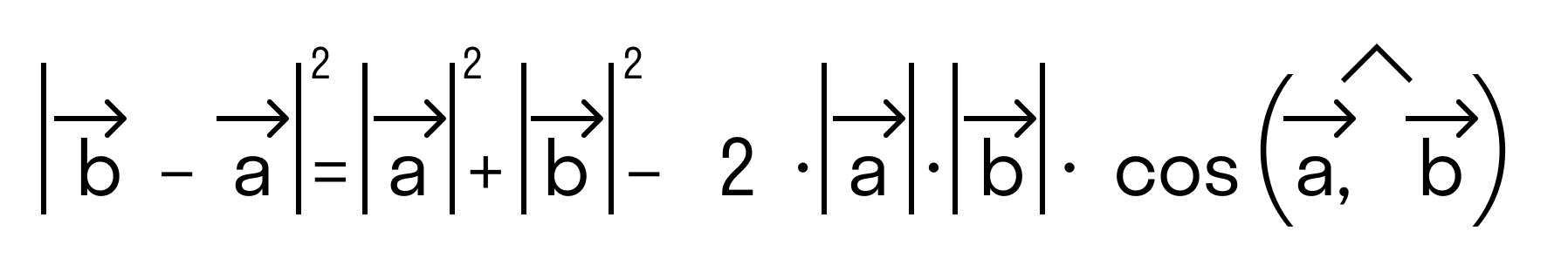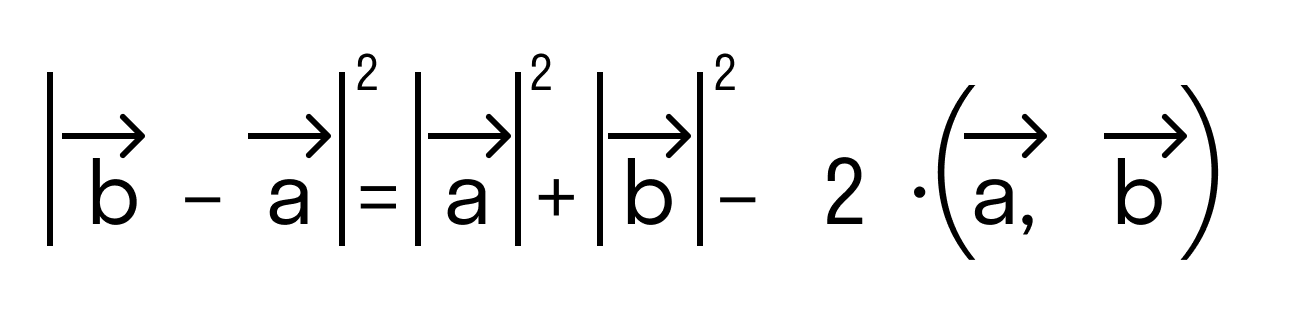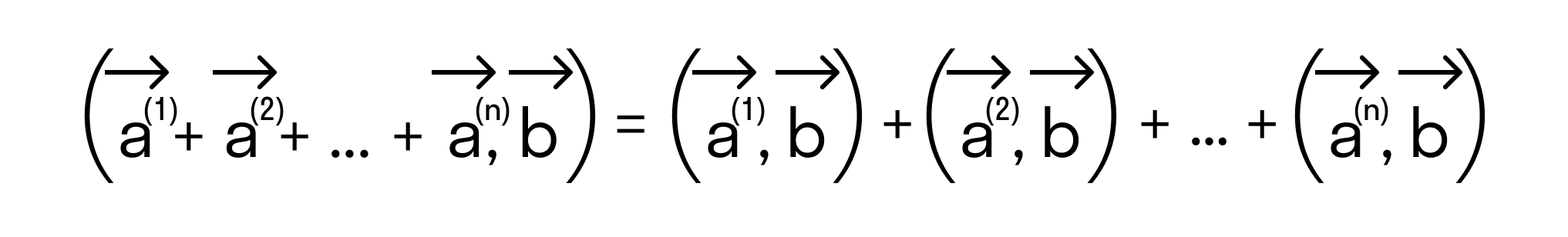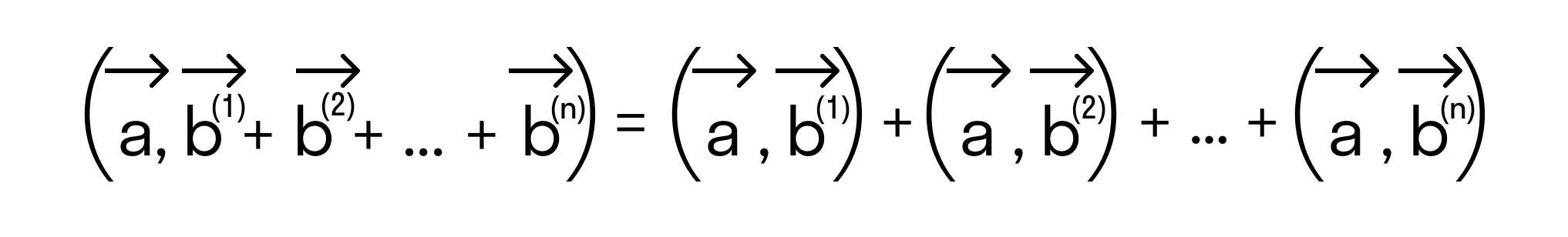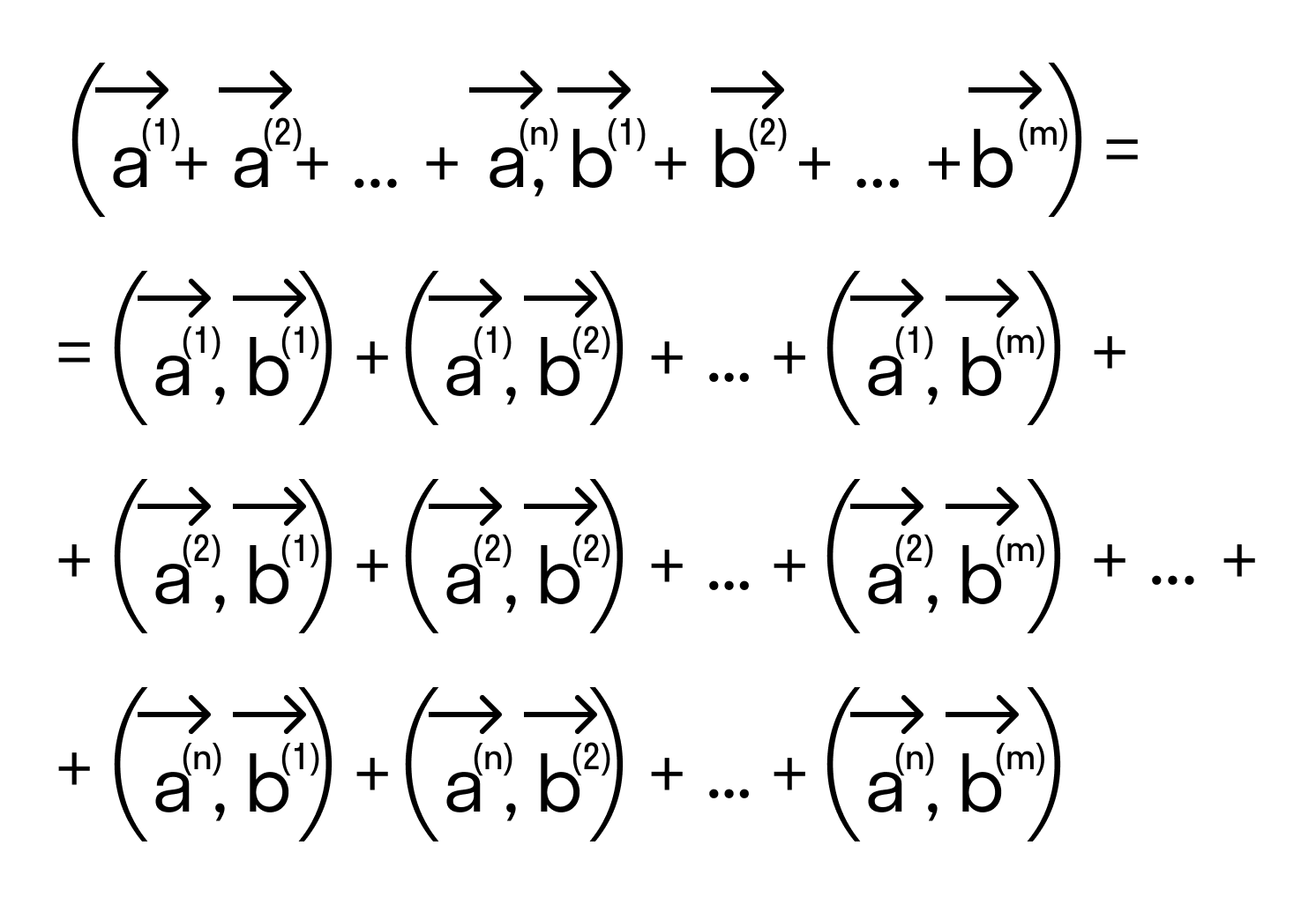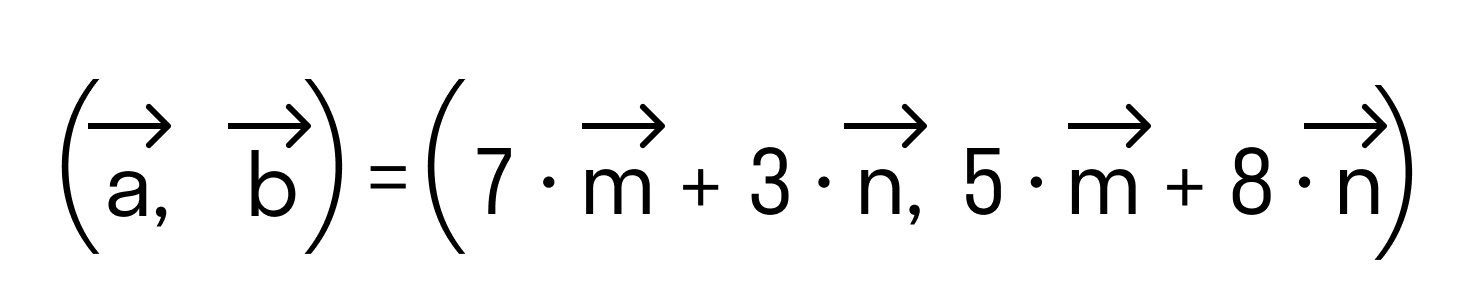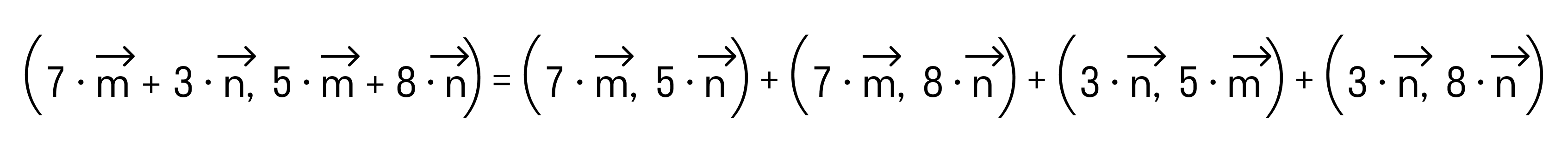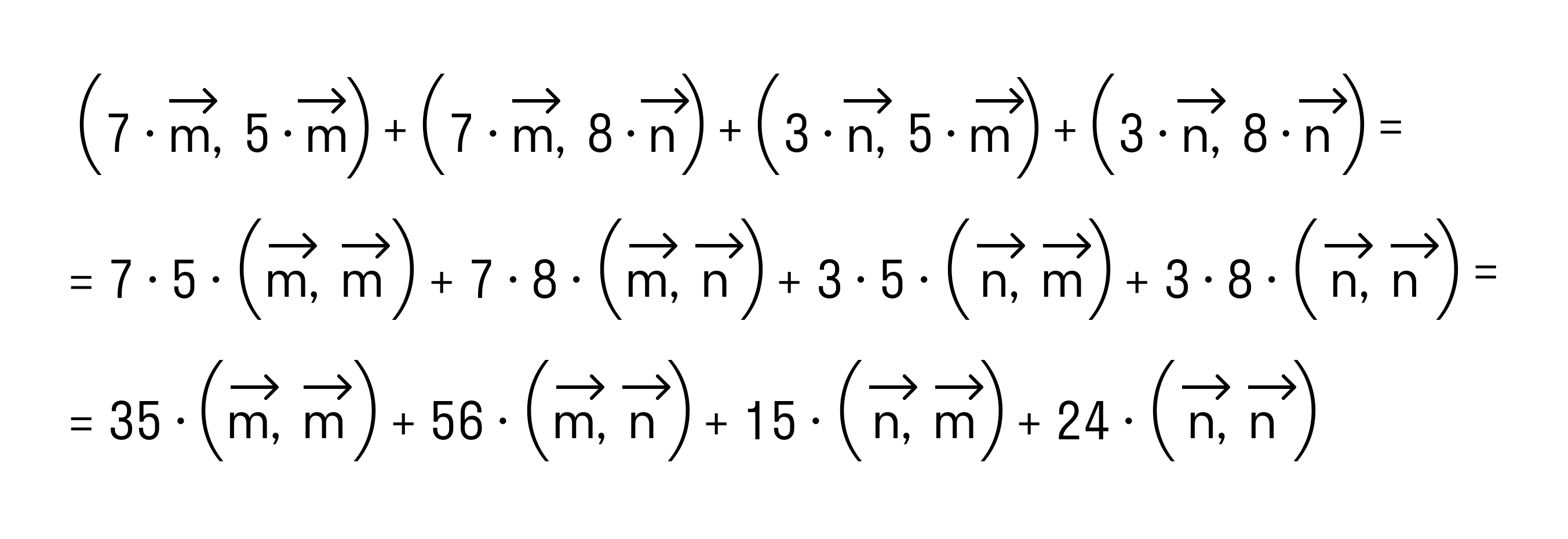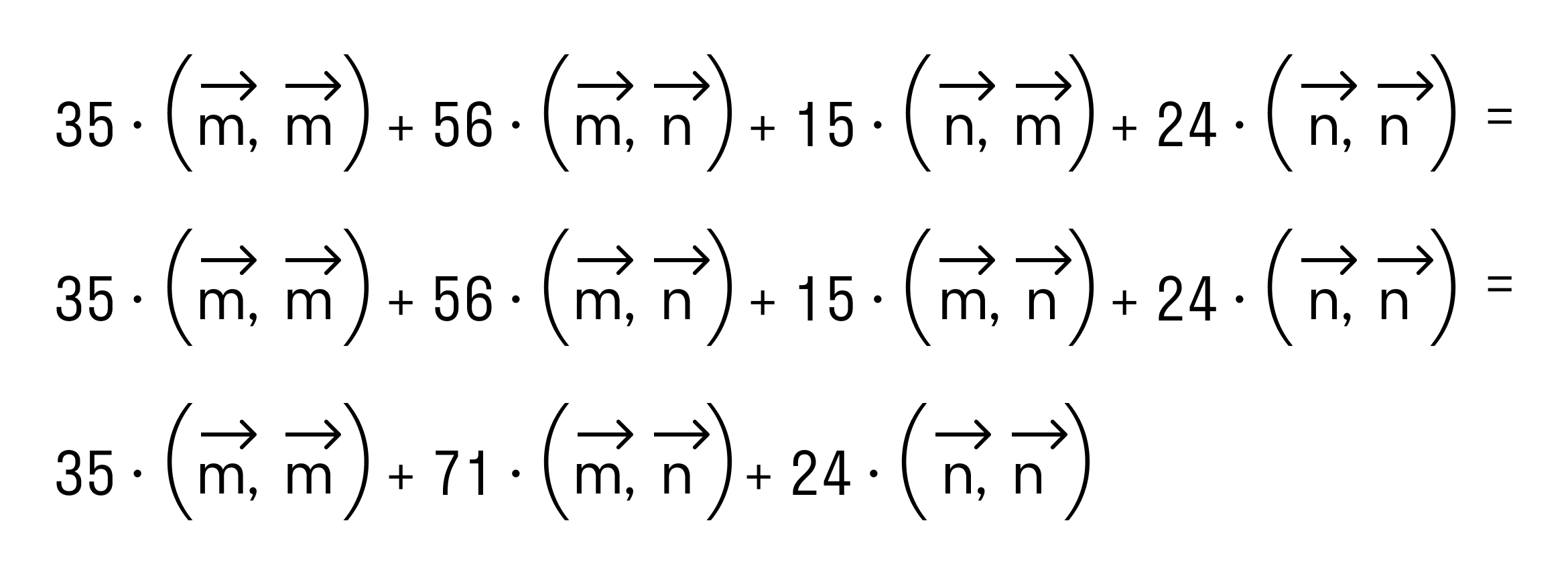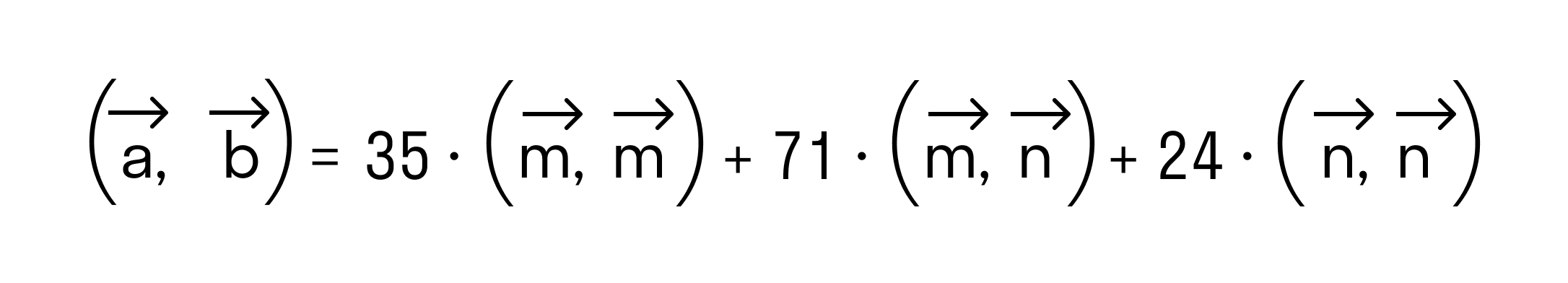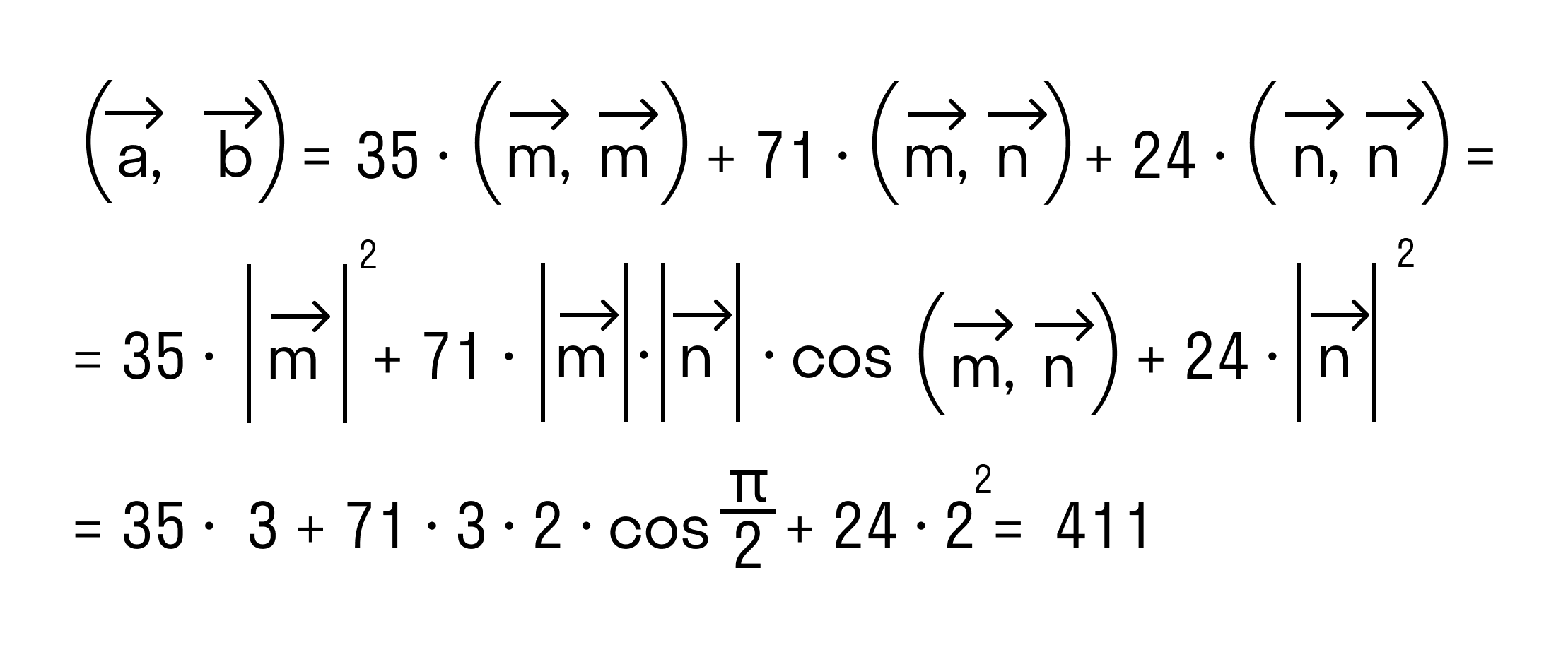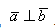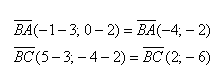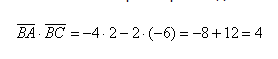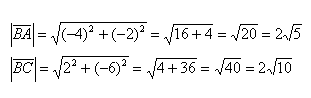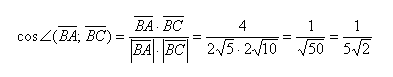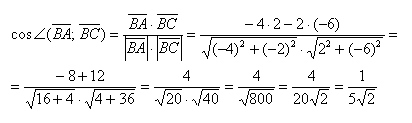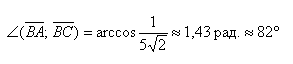вычисление скалярного произведения в координатной форме

08.11.202208.11.2022 admin 0 Comments

Скалярное произведение векторов

Основные определения

Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Как найти координаты точки мы рассказали в этой статье.

Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.

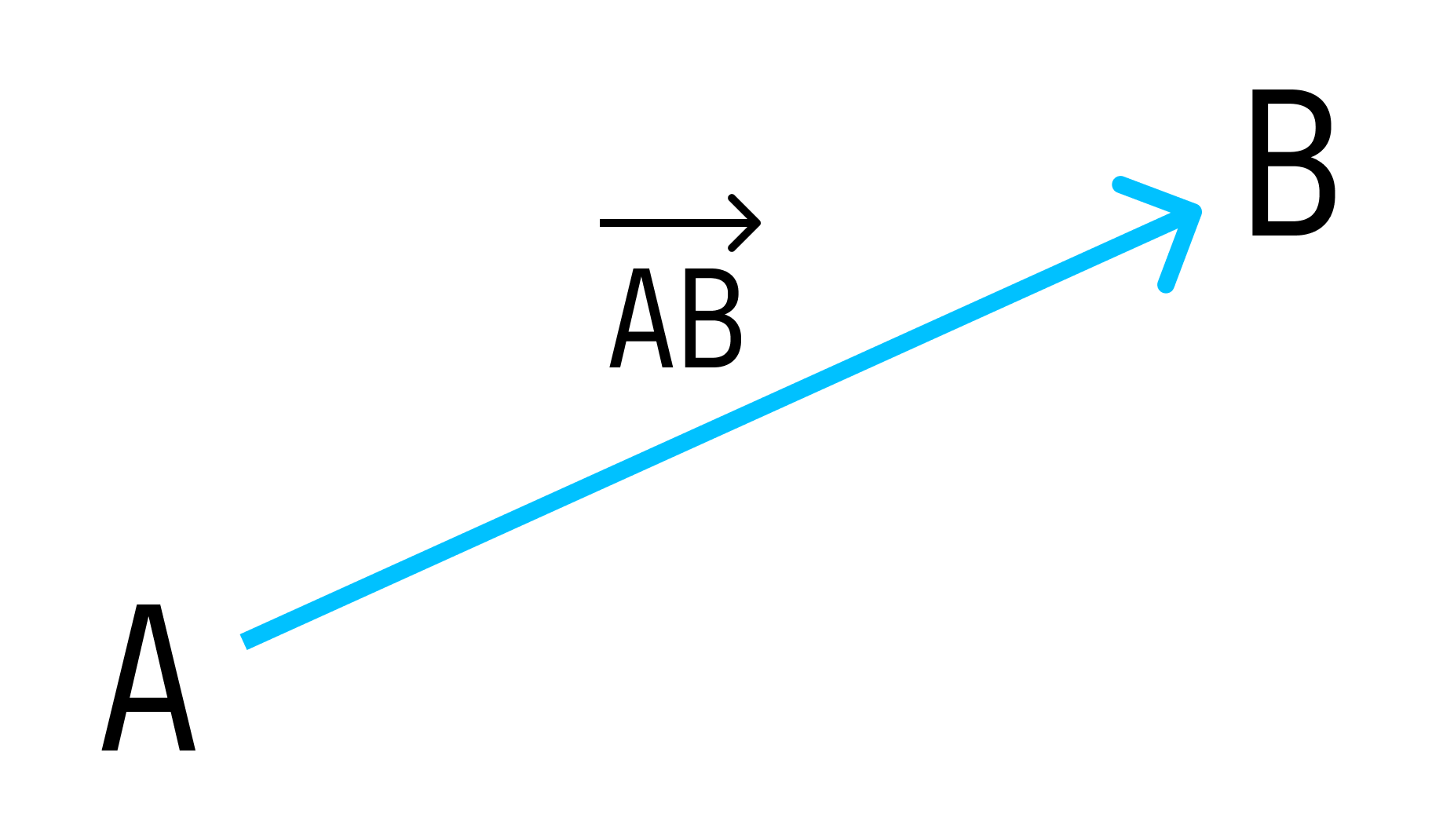
Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.

Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.

Скалярное произведение — это операция над двумя векторами, результатом которой является скаляр, то есть число, которое не зависит от выбора системы координат.

Результат операции является число. То есть при умножении вектор на вектор получается число. Если длины векторов |→a|, |→b| — это числа, косинус угла — число, то их произведение |→a|*|→b|*cos∠(→a, →b) тоже будет числом.

Чтобы разобраться в теме этой статьи, нам еще нужно узнать особенности угла между векторами.

Угол между векторами

Угол между векторами ∠(→a, →b) может принимать значения от 0° до 180° градусов включительно. Аналитически это можно записать в виде двойного неравенства: 0°=

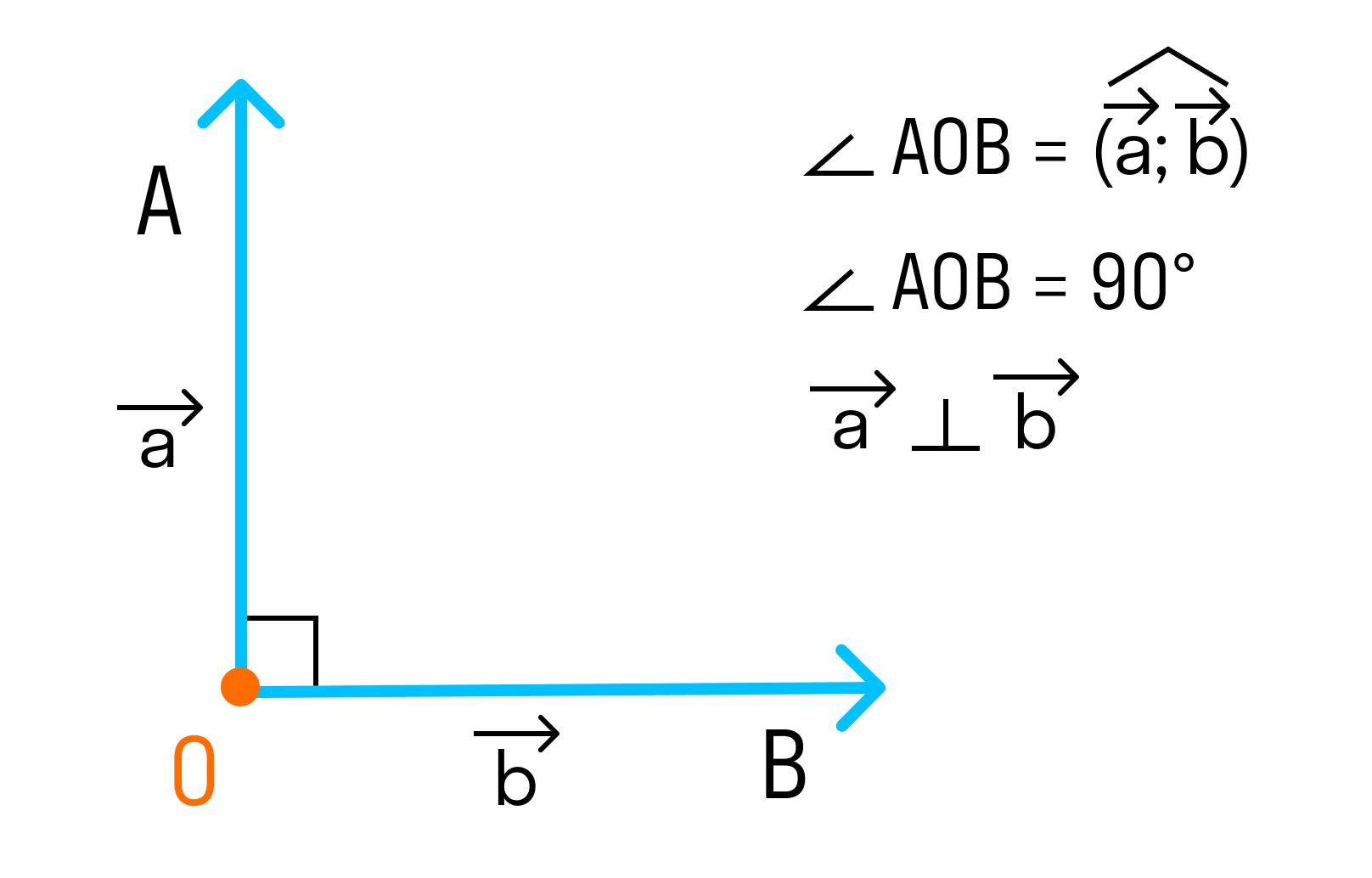
2. Если угол между векторами равен 90°, то такие векторы перпендикулярны друг другу.

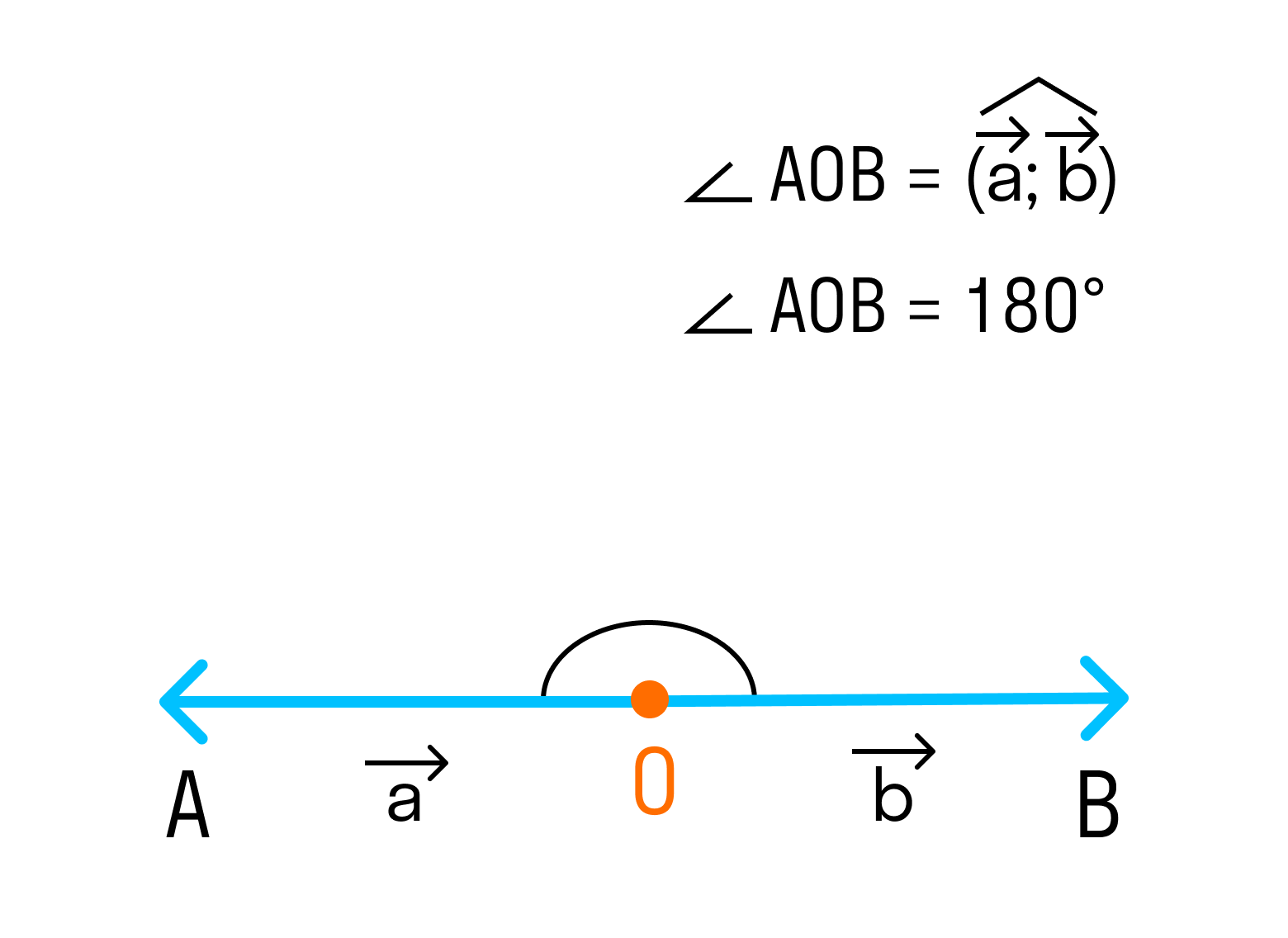
3. Если векторы направлены в разные стороны, тогда угол между ними 180°.

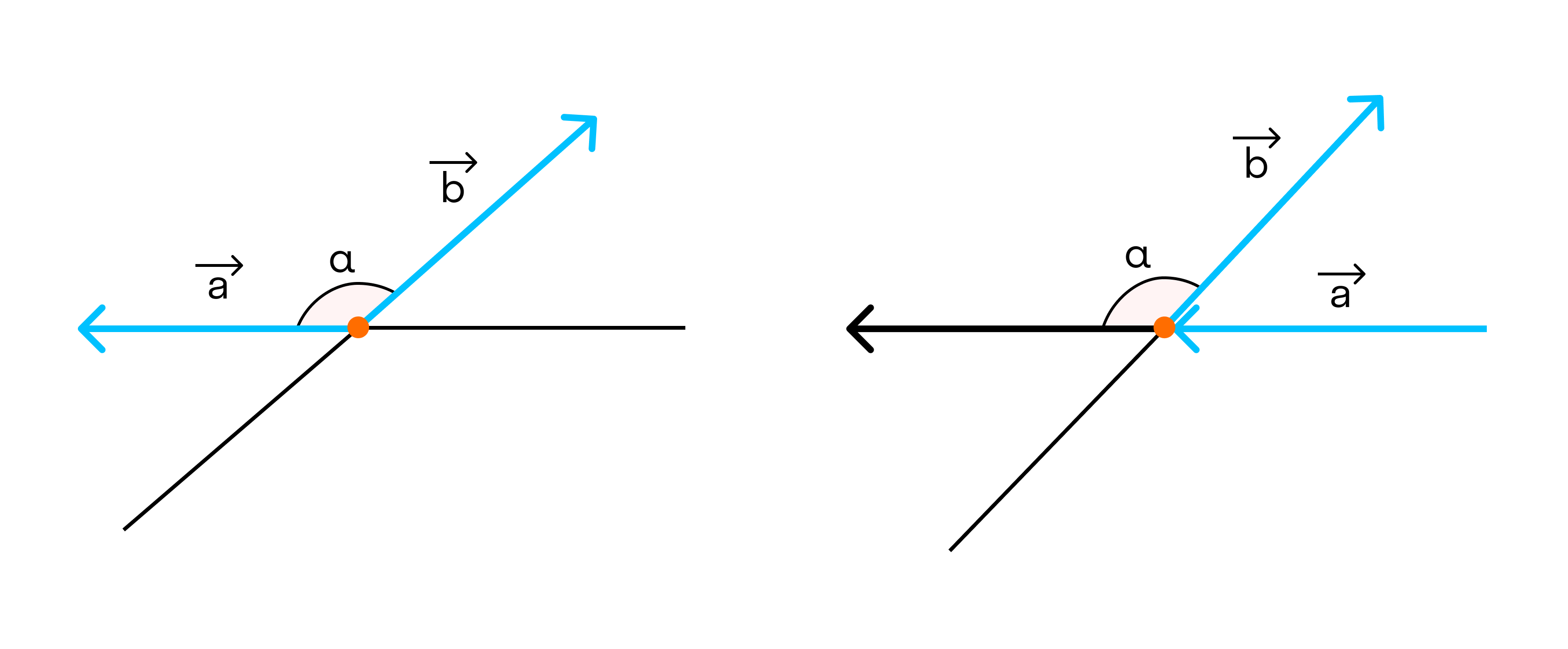
Также векторы могут образовывать тупой угол. Это выглядит так:

Скалярное произведение векторов

Определение скалярного произведения можно сформулировать двумя способами:

Скалярное произведение двух векторов a и b дает в результате скалярную величину, которая равна сумме попарного произведения координат векторов a и b.

Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов, умноженная на косинус угла между ними:

Что важно запомнить про геометрическую интерпретацию скалярного произведения:

Скалярное произведение в координатах

Вычисление скалярного произведения можно произвести через координаты векторов в заданной плоскости или в пространстве.

Скалярным произведением двух векторов на плоскости или в трехмерном пространстве в прямоугольной системе координат называется сумма произведений соответствующих координат векторов →a и →b.

То есть для векторов →a = (ax, ay), →b = (bx, by) на плоскости в прямоугольной декартовой системе координат формула для вычисления скалярного произведения имеет вид: (→a, →b) = ax*bx + ay*by

А для векторов →a = (ax, ay, az), →b = (bx, by, bz) в трехмерном пространстве скалярное произведение в координатах находится так: (→a, →b) = ax*bx + ay*by + az*bz

Докажем это определение:

для векторов →a = (ax, ay), →b = (bx, by) на плоскости, заданных в прямоугольной декартовой системе координат.

Отложим от начала координат (точка О) векторы →OB = →b = (bx, by) и →OA = →a = (ax, ay)

то последнее равенство можно переписать так:

а по первому определению скалярного произведения имеем

Записывайтесь на наши занятия по математике для учеников с 1 по 11 классы! Попробуйте пробный урок!

Формулы скалярного произведения векторов заданных координатами

Формула скалярного произведения векторов для плоских задач

В плоской задаче скалярное произведение векторов a = и b = можно найти по формуле:

a * b = ax * bx + ay * by

Формула скалярного произведения векторов для пространственных задач

В пространственной задаче скалярное произведение векторов a = и b = можно найти по формуле:

a * b = ax * bx + ay * by + az * bz

Формула скалярного произведения n-мерных векторов

Свойства скалярного произведения

Свойства скалярного произведения векторов:

a ≠ 0, b ≠ 0, a * b = 0 a ┴ b

Эти свойства очень легко обосновать, если отталкиваться от определения скалярного произведения в координатной форме и от свойств операций сложения и умножения действительных чисел.

Для примера докажем свойство коммутативности скалярного произведения (→a, →b) = (→b, →a)

По определению (→a, →b) = ax*bx + ay*by и (→b, →a) = bx*ax + by*ay. В силу свойства коммутативности операции умножения действительных чисел, справедливо ax*bx = bx*ax b ay*by = by*ay, тогда ax*bx + ay*by = bx*ax + by*ay.

Следовательно, (→a, →b) = (→b, →a), что и требовалось доказать.

Аналогично доказываются остальные свойства скалярного произведения.

Следует отметить, что свойство дистрибутивности скалярного произведения справедливо для любого числа слагаемых, то есть,

Примеры вычислений скалярного произведения

Пример 1.

Вычислите скалярное произведение двух векторов →a и →b, если их длины равны 3 и 7 единиц соответственно, а угол между ними равен 60 градусам.

У нас есть все данные, чтобы вычислить скалярное произведение по определению:

(→a,→b) = →|a| * →|b| * cos(→a,→b) = 3 * 7 cos60° = 3 * 7 * 1/2 = 21/2 = 10,5.

Ответ: (→a,→b) = 21/2 = 10,5.

Пример 2.

Найти скалярное произведение векторов →a и →b, если →|a| = 2, →|b| = 5, ∠(→a,→b) = π/6.

Используем формулу →a * →b = →|a| * →|b| * cosα.

→a * →b = →|a| * →|b| * cosα = 2 * 5 * cosπ/6 = 10 * √3/2 = 5√3

Пример 3.

Как найти скалярное произведение векторов →a = 7*→m + 3*→n и →b = 5*→m + 8*→n, если векторы →m и →n перпендикулярны и их длины равны 3 и 2 единицы соответственно.

По свойству дистрибутивности скалярного произведения имеем

Сочетательное свойство позволяет нам вынести коэффициенты за знак скалярного произведения:

В силу свойства коммутативности последнее выражение примет вид

Итак, после применения свойств скалярного произведения имеем

Осталось применить формулу для вычисления скалярного произведения через длины векторов и косинус угла между ними:

Пример 4.

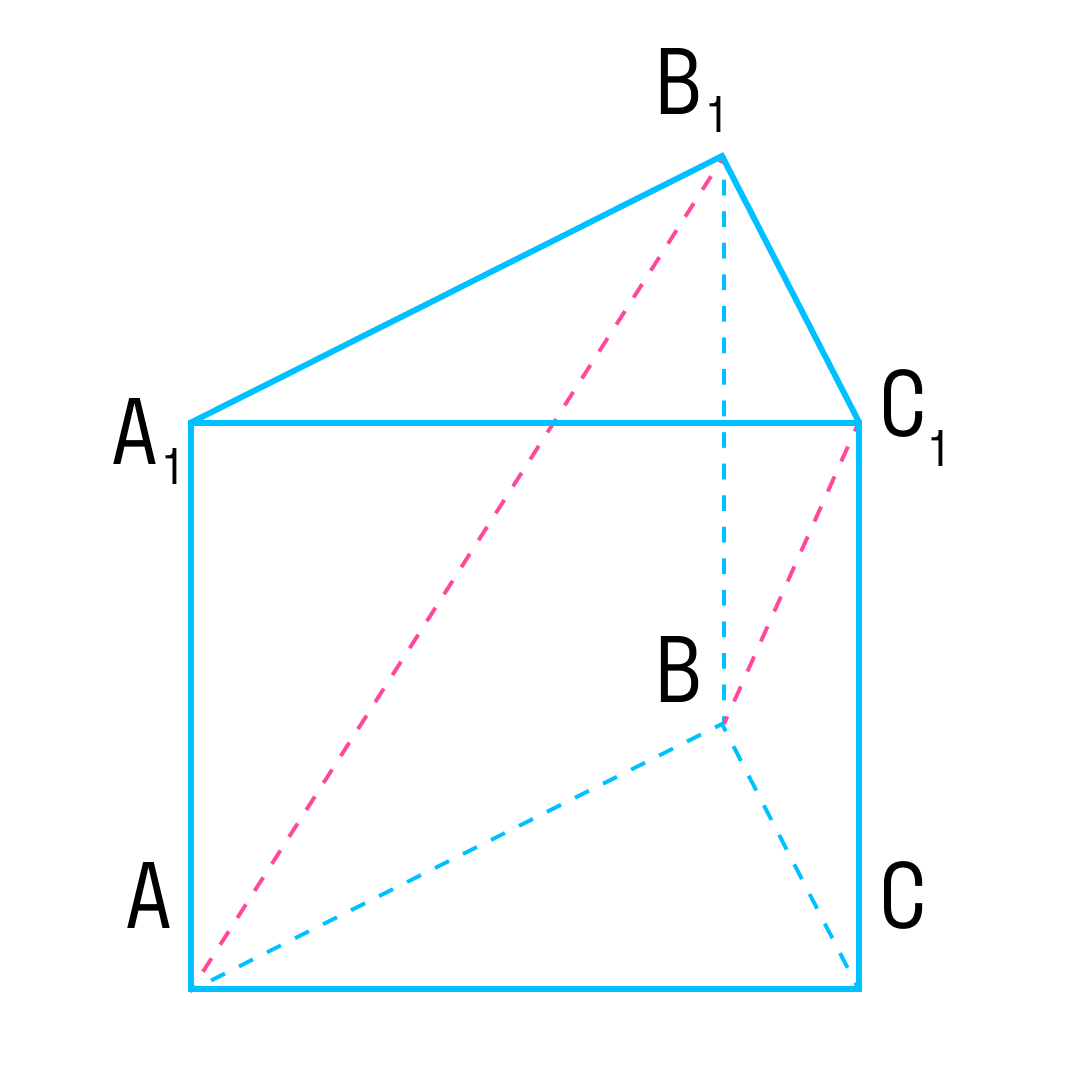
В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найти косинус угла между прямыми AB1 и BC1.

Если сделать выносной рисунок основания призмы, получим понятный плоскостной рисунок с помощью которого можно легко найти координаты всех интересующих точек.

Пример 5.

б) Выяснить, будут ли перпендикулярными отрезки KL и MN, если K(3;5), L(-2;0), M(8;-1), N(1;4).

а) Выясним, будут ли ортогональны пространственные векторы. Вычислим их скалярное произведение: →ab = 1*6 + 2*(-1) + (-4)*1 = 0, следовательно

Обратите внимание на два существенных момента:

Ответ: а) →a перпендикулярно →b, б) отрезки KL, MN не перпендикулярны.

Пример 6.

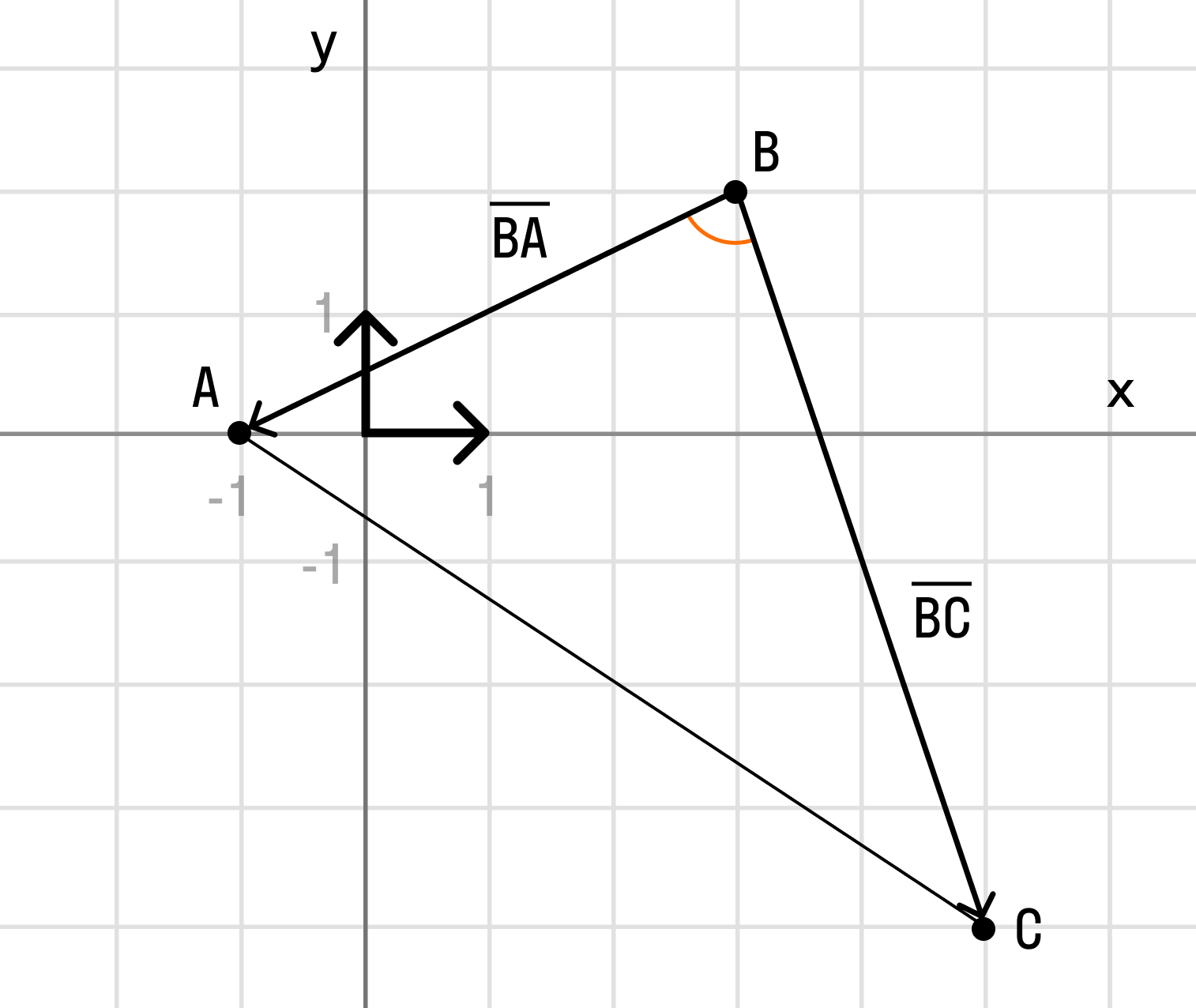
По условию чертеж выполнять не требуется, но для удобства можно сделать:

Требуемый угол ∠ABC помечен зеленой дугой. Сразу вспоминаем школьное обозначение угла: ∠ABC — особое внимание на среднюю букву B — это и есть нужная нам вершина угла. Для краткости можно также записать просто ∠B.

Из чертежа видно, что угол ∠ABC треугольника совпадает с углом между векторами →BA и →BC, иными словами: ∠ABC = ∠(→BA; →BC).

Вычислим скалярное произведение:

Вычислим длины векторов:

Найдем косинус угла:

Когда такие примеры не будут вызывать трудностей, можно начать записывать вычисления в одну строчку:

Полученное значение не является окончательным, поэтому нет особого смысла избавляться от иррациональности в знаменателе.

Если посмотреть на чертеж, то результат действительно похож на правду. Для проверки угол также можно измерить и транспортиром.

Ответ: ∠ABC = arccos(1/5√2) ≈1,43 рад. ≈ 82°

Важно не перепутать, что в задаче спрашивалось про угол треугольника, а не про угол между векторами. Поэтому указываем точный ответ: arccos(1/5√2) и приближенное значение угла: ≈1,43 рад. ≈ 82°, которое легко найти с помощью калькулятора.

А те, кому мало и хочется еще порешать, могут вычислить углы ∠A, ∠C, и убедиться в справедливости канонического равенства ∠A + ∠B + ∠C = 180°.

Источник

Вектор. Скалярное произведение векторов. Угол между векторами.

Скалярным произведением (или внутренним произведением) 2 векторов есть операция с двумя

векторами, итогом чего является число (скаляр), которое не зависит от системы координат и которое

характеризует длины векторов-сомножителей и угол между векторами.

Также скалярным произведением двух векторов называется число, которое

равно произведению модулей 2 векторов на косинус угла между векторами.

Скалярное произведение векторов формула:

Этой операции соответствует умножение длины вектора x на проекцию вектора y на вектор x. Эта

операция зачастую рассматривается как коммутативная и линейная по каждому из сомножителей.

Скалярное произведение векторов ,, обозначается так: (порядок записи сомножителей не имеет

значения, т.е. ).

Еще используются такие обозначения: , , .

В основном имеется ввиду, что скалярное произведение определено положительно, т.е.

при каждом . Если этого не иметь ввиду, то произведение зовется индефинитным

(неопределенным).

Если хотя бы один из 2 векторов или равен нулевому вектору (равен нулю), то .

Свойства скалярного произведения векторов.

1. — симметричность.

2. обозначается и зовется скалярный квадрат.

3. Если , то

4. Если и и и , то . Обратное утверждение тоже соответствует

Если же векторы и заданы своими координатами: , , то: скалярное

произведение векторов, формула:

Формула для определения длины вектора:

Длина (модуль) вектора, с известными координатами, равен квадратному корню из суммы квадратов

Длина вектора , заданного своими координатами, равна:

Как определить угол между 2 векторами:

Как найти угол между двумя векторами , , формула:

Ежели угол меж двумя векторами острый, то их скалярное произведение имеет положительный знак; если

же угол между двумя векторами тупой, то их скалярное произведение имеет отрицательный знак.

Скалярное произведение двух ненулевых векторов равно нулю, тогда и только тогда, когда эти векторы

ортогональны.

Альтернативное определение скалярного произведения векторов (вычисление скалярного

произведения двух векторов, заданных своими координатами).

Вычислить координаты вектора, если заданы координаты его начала и его конца очень просто. Давайте

рассмотрим этот вопрос:

Исходя из этого, координаты вектора АВ:

Точно так же и в двухмерном пространстве – разница в отсутствии третьих координат.

Итак, предположим, даны два вектора, которые заданы набором координат своих точек:

а) В двухмерном пространстве (плоскость):

Значит, скалярное произведение этих векторов вычислим по формуле:

б) В трехмерном пространстве:

Как и в двухмерном случае, скалярное произведение двух векторов вычисляем по формуле:

Источник

Геометрия. 11 класс

Конспект урока

Геометрия, 11 класс

Урок № 2. Скалярное произведение векторов

Перечень вопросов, рассматриваемых в теме:

— ввести понятие угла между векторами и скалярного произведения векторов, рассмотреть формулу скалярного произведения в координатах;

— показать применение скалярного произведения векторов при решение задач.

— рассмотреть основные свойства скалярного произведения;

— сформировать умения вычислять скалярное произведение векторов и находить угол между векторами;

— показать, как используется скалярное произведение векторов при решении задач на вычисление углов между двумя прямыми, а также между прямой и плоскостью.

Два вектора называются перпендикулярными, если угол между ними равен 90°.

Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними.

Формула вычисления скалярного произведения векторов по определению:

Формула вычисления скалярного произведения векторов через координаты:

Открытые электронные ресурсы:

Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/

Теоретический материал для самостоятельного изучения

Работа по теме урока. Объяснение новой темы

Угол между векторами

Если векторы не являются сонаправленными, то лучи ОА и ОB образуют угол АОВ.

Определение: Два вектора называются перпендикулярными, если угол между ними равен 90°.

Скалярное произведение векторов:

Определение: Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними. Запишем формулу:

Утверждение1. Скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.

Утверждение2. Скалярный квадрат вектора равен квадрату его длины.

Формула скалярного произведения двух векторов и

Через их координаты

Скалярное произведение двух векторов равно сумме произведений соответствующих координат этих векторов.

Угол между векторами.

Косинус угла между векторами пространства , заданными в ортонормированном базисе , выражается формулой:

Сформулируем основные свойства скалярного произведения векторов.

Для любых векторов и любого числа k справедливы равенства:

1) причем при

2) (переместительный закон).

3) (распределительный закон).

4) (сочетательный закон).

Вычисление углов между прямыми и плоскостями.

Угол между двумя прямыми (пересекающимися или скрещивающимися), если известны координаты направляющих векторов.

Примеры и разбор решения заданий тренировочного модуля

Дано: прямоугольный параллелепипед, где . Найти и .

Решение: ранее в таких случаях мы пытались по рисунку находить величины углов.

Но теперь мы владеем формулой косинуса угла между прямыми.

Для удобства изобразим прямоугольную систему координат так, чтобы точка B совпадала с точкой начала координат. Взяв длину рёбер AB и BC за единичные отрезки, можно утверждать, что длина отрезка BB равна 2.

Тогда не трудно определить координаты точек B, D, C и D₁.

Теперь не трудно найти координаты векторовBD и CD как разности соответствующих координат конца и начала вектора.

Получаем, что вектор BD <1-0;1-0;0-0>. А вектор

Теперь можем воспользоваться формулой косинуса угла между прямыми. Подставим координаты направляющих векторов.