вычислить интеграл по замкнутому контуру с помощью основной теоремы о вычетах

Электронная библиотека

Определение. Точки комплексной плоскости, в которых однозначная функция f(z) является аналитической, называют правильными точками этой функции, а точки, в которых f(z) не является аналитиче­ской, называют особыми точками (в частности, точки, в которых f(z) не определена).

Определение. Точка z₀ называется нулем (корнем) порядка (кратности) аналитической функции f(z),если:

б) существует, конечен и не равен нулю.

Определение. Пусть f(z) аналитическая функция в окрестности точки z₀, за ис­ключением самой точки z₀. В этом случае точка z₀ называется изолированной особой точкой функции f(z).

Различают изолированные особые точки одно­значной функции трёх типов:

2) полюс k-го порядка – изолированную особую точку z₀, в которой существует конечный предел, не равный нулю:

3) сущест­венно особую точку – изолированную особую точку z₀, которая не является ни уст­ранимой, ни полюсом. То есть не существует, ни конечный, ни бесконечный.

Теорема (о связи между нулем и полюсом). Если точка z₀ – нуль порядка к функции f(z), то для функции 1/f(z) эта точка является полюсом порядка к.

Пусть f(z) – функция, аналитическая в каждой точке об­ласти D, за исключением конечного числа изолированных осо­бых точек, и L — кусочно-гладкий замкнутый контур, целиком лежащий в области D и не проходящий через особые точки функции f(z).

Если в области, ограниченной контуром L, не содержится особых точек функции f(z), то по основной теореме Коши

Если же в области, ограниченной контуром L, имеются особые точки функции f(z), то значение этого интеграла, вообще говоря, отлично от нуля.

Вычет f(z) относительно точки z₀ обозначается симво­лом resf(z₀)(Resf(z₀)) или так, что имеем:

Вычет функции относительно устранимой особой точки равен нулю:

Вычет f(z) относительно простого полюса можно найти по формуле:

Вычет f(z) относительно полюса порядка к находят по формуле:

Эта теорема имеет большое значение для приложений.

Од­но из них – это вычисление некоторых интегралов от функции комплексной переменной.

Замечание. В предыдущих рассуждениях о вычетах неявно предпола­галось, что рассматриваются конечные изолированные особые точки (это ясно из того, что интеграл по замкнутому контуру по умолчанию брался в положительном направлении, т.е. против часовой стрелки, а особая точка при этом попадает внутрь конту­ра только в случае, когда она конечна). В случае же, когда рас­сматривается бесконечно удаленная точка, ситуация несколько иная. Точнее, сформулируем это так.

Определение. Вычетом функции f(z) относительно бесконечно уда­ленной точки называют интеграл:

Найти интеграл от функции комплексного переменного, используя основную теорему Коши о вычетах:

Решение

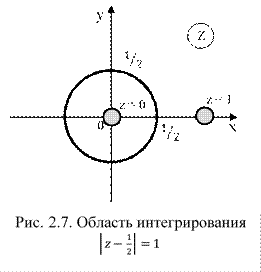
1) Определим изолированные особые точки подинтегральной функции, согласно теореме (2.47):

2) Определим точки, лежащие внутри области интегрирования, изобразим область графически (рис. 2.7).

3) Определим тип рассматриваемой изолированной особой точки z = 0. Найдем предел по формуле (2.41):

Так как предел существует, то z = 0 – полюс первого порядка (простой полюс).

4) Найдем вычет функции относительно простого полюса z = 0, используя формулу (2.44):

5) Определим значение интеграла по основной теореме Коши о вычетах (2.47):

Найти интеграл от функции комплексного переменного, используя основную теорему Коши о вычетах:

Решение

1) Определим изолированные особые точки подинтегральной функции, согласно теореме (2.47):

2) Определим точки, лежащие внутри области интегрирования, изобразим область (рис. 2.8).

Обе особые точки лежат внутри области интегрирования.

4) Найдем вычеты функции относительно простых полюсов и используя формулу (2.44):

5) Определим значение интеграла по основной теореме Коши о вычетах (2.47)

Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00

Источник

Математика Решение типового варианта контрольной работы

Задание 12. Вычислить интегралы, используя теорему Коши о вычетах:

Определим вид особых точек и найдем в них вычеты.

Задание 13. Вычислить интегралы с помощью вычетов.

а) Сформулируем правило, позволяющее вычислять несобственные интегралы от рациональной функции действительного переменного с помощью теории функций комплексного переменного:

где означает сумму вычетов функции по всем полюсам, расположенным в верхней полуплоскости.

б) Сформулируем правило, позволяющее вычислить рассматриваемый несобственный интеграл с помощью теории функций комплексного переменного:

где означает сумму вычетов функции по всем полюсам, расположенным в верхней полуплоскости.

в) Сформулируем правило, позволяющее вычислить определенный интеграл функции, зависящей рационально от тригонометрических функций с помощью теории функций комплексного переменного:

Задание 3. Указать область дифференцируемости функции и вычислить производную. Выделить действительную и мнимую часть полученной производной.

Задание 4. Определить вид кривой

Задание 10. Для функции найти изолированные особые точки, провести их классификацию, вычислить вычеты относительно найденных точек.

Задание 11. Вычислить интеграл от функции комплексного переменного:

Задание 12. Вычислить интегралы, используя теорему Коши о вычетах.

Задание 13. Вычислить интегралы с помощью вычетов.

Источник

Вычеты. Основная теорема о вычетах

Содержание:

По этой ссылке вы найдёте полный курс лекций по математике:

] в лорановском разложении этой функции в точке z0. Отсюда, в частности, вытекает, что вычет в устранимой особой точке равен нулю. Укажем некоторые формулы для вычисления вычета в полюсе функции /(г).

Поэтому по теореме Коши для многосвязной области имеем Из этой формулы, пользуясь определением вычета получаем требуемое равенство (5). 6.1. Вычет функции относительно бесконечно удаленной точки Говорят, чтофункция f(z) является аналитической в бесконечно удаленной точке z = оо, если функция аналитична вточке С =0. Это следует понимать так: функцию g(0= f (f) можно доопределить до аналитической, положив Например, функция аналитична в точке z = оо, поскольку функция аналитична в точке С = 0.

Возможно вам будут полезны данные страницы:

Пусть функция /(г) аналитична в некоторой окрестности бесконечно удаленной точки (кроме самой точки z = оо). Точка z = оо называется изолированной особой точкой функции /(г), если в некоторой окрестности этой точки нет других особых точек функции f(z). Функция имеет в бесконечности неизолированную особенность: полюсы zk = к-к этой функции накапливаются в бесконечности, если к оо. Говорят, что z — оо является устранимой особой тонкой, полюсом или существенно особой точкой функции f(z) в зависимости от того, конечен, бесконечен или вовсе не существует lim f(z).

Критерии типа бесконечно удаленной точки, связанные с разложением Лорана, изменяюгся по сравнению с критериями для конечных особых точек. Теорема 22. Если z — оо является устранимой особой точкой функции /(z), то лоранов-ское разложение f(z) в окрестности этой точки не содержит полож и тельных степеней z;eaiu z — оо — полюс, то это разложение содержит конечное число положительных степеней z, в случае существенной особенности — бесконечное число положительных степеней z.

При этом лорановским разложением функции /(z) в окрестности бесконечно удаленной точки будем называть разложение в ряд Лорана, сходящийся всюду вне круга достаточно большого радиуса R с центром в точке z — 0 (кроме, быть может, самой точки z — оо). Пусть функция f(z) — аналитична в некоторой окрестности точки z = оо (кроме, быть может, самой этой точки). Вычетом функции /(z) в бесконечности называют величину пае 7 — достаточно большая окружность \z\ = р, проходимая по часовой стрелке (так, что окрестность точки z — оо остается слева, как и в случае конечной точки г = го).

И з этого определения следует, что вычет функции в бесконечности равен коэффициенту при z

Известные тейлоровские разложения функций е1, cosz, sinz, chz, shz можно рассматривать также и как лорановские разложения в окрестности точки z — оо.

Так как все эти разложения содержат бесконечное множество положительных степеней z, то перечисленные функции имеюгвточке z = оо существенную особенность. Теорема 23. Если функция f(z) имеет в расширенной комплексной плоскости конечное число особых точек, то сумма всех ее вычетов, включая и вычет в бесконечности, равна нулю. Так что, если — конечные особые точки функции f

Пример 4:

Вычислить интеграл Полюсами (конечными) подынтегральной функции являются корни zt уравнения гя = —1, которые все лежат внутри окружности В окрестности точки г = оо функция /(z) имеет следующее разложение: ИЗ КОТОРОГО ВИДНО, ЧТО В силу теоремы 6.2. Приложение вычетов к вычислению определенных интегралов. Интегралы от рациональных функций Теорема 24. Пусть f(x) — рациональная функция, т. е. где — многочлены степеней пит соответственно.

Пример 5:

Пример 6. Вычислить интеграл Применяя подстановку z = е,г. после простых преобразований (см. формулы (II)) получим, что Внутри единичного круга при условии находится только один полюс (второго порядка) Вычет функции Интегралы вида гдеД(х) — правильная рациональная дробь, а > 0 — вещественное число. При вычислении таких интегралов часто бывает полезной следующая лемма. Лемма Жордана. Пусть функция f(z) аналитична в верхней полуплоскости исключением конечного числа изолированных особых точек, и при \ стремится к нулю равномерно относительно arg z.

где 7л — верхняя полуокружность Условие равномерного стремления /(г) к нулю означает, что на полуокружности 7R Оценим исследуемый интефал. Замечая, что на 7Л В силу известного неравенства (см. рис. 31) справедливого при (для доказательства достаточно заметить, что и, значит, функция ^ убывает на полуинтервале Сопоставляя формулы (13) и (14), заключаем, что 4 Введем вспомогательную функцию Пример 7. Вычислить интеграл Нетрудно видеть, что если г = х, то Jmh(z) совпадает с подынтегральной функцией.

Отсюда откуда Упражнения Найдите действительную и мнимую части функдаи: Найдите образы действительной и мнимой осей при отображении: Докажи те, что функция непрерывна на всей комплексной плоскости: Пользуясь условиями Коши—Римана, выясните, является ли функция аналитической хотя бы в одной точке или нет: Восстановите аналитическую в окрестности точки 20 функцию /(г) по известной действительной части и (или по известной мнимой части v(x, у)) и значению f(z0):

Покажите, что следующие функци и являются гармоническими: Может ли данная функция быть действительной или мнимой частью аналитической функции Найдите действительную и мнимую части функции: Найдите модуль и главное значение аргумента функции в указанной точке zq: Найдите логарифмы следующих чисел: Решите уравнение: 38. Вычислите интеграл /— линия, соединяющая точки z\ = 0 отрето к прямой, б) дуга параболы ломаная 39. Вычислите интеграл — полуокружность Вычислите интегралы: 43.

Вычислите интеграл / где 7 — верхняя половина окру*« ости |z| = 1 (выбирается Вычеты Основная теорема о вычетах Применение вычетов к вычислению интегралов Вычет функции относительно бесконечно удаленной точки Приложение вычетов к вычислению определенных интегралов Интегралы от рациональных функций Лемма Жордана Вычисление интегралов Френеля ветвь функци и л/z, для которой 44. Вычислите интеграл / ^ dz, где 7 — отрезок прямой, идущий из точки zj = 1 в точку.

Вычислите интегралы: Найдите радиус сходимости ряда: Рашожите функцию в ряд Тейлора и найдите радиус сходимости полученного ряда: постепеням z + I. 55. cosz постепеням 56.—-— постепеням z + 2. 57.—^— постепеням z. 58. sh2 z постепеням z. Найдите нули функции и определите их порядки: z Определите область сходимости ряда: Разложите в ряд Лорана в окрестности точки г = 0: Разяожитс в ряд Лорана в уюзан ном кольце: Найдите особые точки и определит е их характер:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник