выполнить действия над комплексными числами в тригонометрической форме

Комплексные числа

Формы

Так сложилось в математике, что у данных чисел несколько форм. Число одно и тоже, но записать его можно по-разному:

Далее с примерами решений вы узнаете как переводить комплексные числа из одной формы в другую путем несложных действий в обе стороны.

Изображение

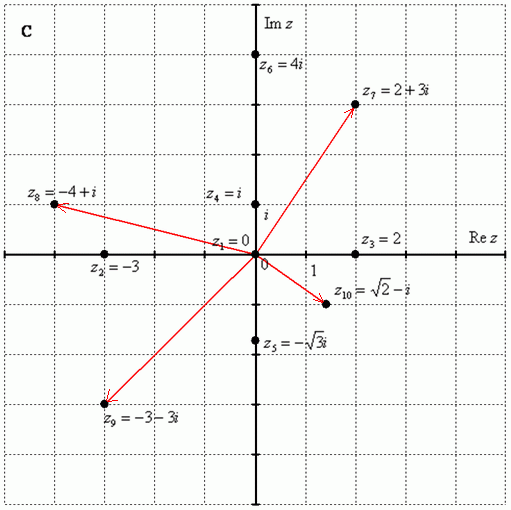
Изучение выше мы начали с алгебраической формы. Так как она является основополагающей. Чтобы было понятно в этой же форме изобразим комплексное число на плоскости:

Вычислить сумму и разность заданных комплексных чисел:

Сначала выполним сложение. Для этого просуммируем соответствующие мнимые и вещественные части комплексных чисел:

Аналогично выполним вычитание чисел:

Выполнить умножение и деление комплексных чисел:

Так, теперь разделим первое число на второе:

Суть деления в том, чтобы избавиться от комплексного числа в знаменателе. Для этого нужно домножить числитель и знаменатель дроби на комплексно-сопряженное число к знаменателю и затем раскрываем все скобки:

Разделим числитель на 29, чтобы записать дробь в виде алгебраической формы:

Для возведения в квадрат достаточно умножить число само на себя:

Пользуемся формулой для умножения, раскрываем скобки и приводим подобные:

В этом случае не всё так просто как в предыдущем случае, когда было возведение в квадрат. Конечно, можно прибегнуть к способу озвученному ранее и умножить число само на себя 7 раз, но это будет очень долгое и длинное решение. Гораздо проще будет воспользоваться формулой Муавра. Но она работает с числами в тригонометрической форме, а число задано в алгебраической. Значит, прежде переведем из одной формы в другую.

Вычисляем значение модуля:

Найдем чем равен аргумент:

$$ \varphi = arctg \frac<3> <3>= arctg(1) = \frac<\pi> <4>$$

Записываем в тригонометрическом виде:

Преобразуем в алгебраическую форму для наглядности:

Представим число в тригонометрической форме. Найдем модуль и аргумент:

Используем знакомую формулу Муавра для вычисления корней любой степени:

Источник

Тригонометрическая форма комплексного числа

Рассмотрим комплексное число, заданной в обычной (алгебраической) форме:

Задача заключается в представлении комплексного числа (1) в тригонометрической форме. Для этого на комплексной плоскости введем полярные координаты. Примем за полюс начало координат, а за полярную ось вещественную ось R.

Как известно, полярными координатами точки z являются длина r ее радиус-вектора, равной расстоянию от точки z до полюса, и величина ее полярного угла, т.е. угла, образованного между полярной осью и вектором-радиусом точки z. Отметим, что направление отсчета угла берется от полярной оси до вектора-радиуса против часовой стрелки (Рис.1, Рис.2).

На Рис.3 изображено комплексное число z. Координаты этого числа в декартовой системе координат (a, b). Из определения функций sin и cos любого угла, следует:

Подставляя (2) в (1), получим:

Эта форма записи называется тригонометрической формой записи комплексного числа.

Уравнения (2) возведем в квадрат и сложим:

.

r−длина радиус-вектора комплексного числа z называется модулем комплексного числа и обозначается |z|. Очевидно |z|≥0, причем |z|=0 тогда и только тогда, когда z=0.

Величина полярного угла точки, соответвующей комплексному числу z, т.е. угла φ, называется аргументом этого числа и обозначается arg z. Заметим, что arg z имеет смысл лишь при z≠0. Аргумент комплексного числа 0 не имеет смысла.

Аргумент комплексного числа определен неоднозначно. Если φ аргумент комплексного числа, то φ+2πk, k=0,1. также является аргументом комплексного числа, т.к. cos(φ+2πk)=cosφ, sin(φ+2πk)=sinφ.

Приведение комплексного числа из алгебраической формы в тригонометрическую

Пусть комплексное число представлено в алгебраической форме: z=a+bi. Представим это число в тригонометрической форме. Вычисляем модуль комплексного числа: . Вычисляем аргумент φ комплексного числа из выражений или . Полученные значения вставляем в уравнение (3).

Пример 1. Представить комплексное число z=1 в тригонометрической форме.

Решение. Комплексное число z=1 можно представить так: z=1+0i. Вычислим модуль этого числа: . Вычислим аргумент этого числа: cosφ=1/1. Откуда имеем φ=0. Подставляя значения модуля и аргумента в (3), получим: z=1(cos0+isin0).

Пример 2. Представить комплексное число z=i в тригонометрической форме.

Решение. Комплексное число z=i можно представить так: z=0+1i. Вычислим модуль этого числа: . Вычислим аргумент этого числа: cosφ=0/1. Откуда имеем φ=π/2. Подставляя значения модуля и аргумента в (3), получим: .

Ответ. .

Пример 3. Представить комплексное число z=4+3i в тригонометрической форме.

Решение. Вычислим модуль этого числа: . Вычислим аргумент этого числа: cosφ=4/5. Откуда имеем φ=arccos(4/5). Подставляя значения модуля и аргумента в (3), получим: .

Ответ. , где φ=arccos(4/5).

Умножение комплексных чисел в тригонометрической форме записи

В результате умножения комплексных чисел в тригонометрической форме мы получили комплексное число в тригонометрической форме, следовательно |z₁z₂|=r₁r₂, или

Пример 4. Умножить комплексные числа и .

Решение. Воспользуемся формулой (5):

Ответ. .

Деление комплексных чисел в тригонометрической форме записи

Отсюда следует, что или

Далее , или

Пример 5. Делить комплексные числа и .

Решение. Воспользуемся формулой (8):

Ответ. .

Источник

Алгебра и начала математического анализа. 11 класс

Конспект урока

Алгебра и начала математического анализа, 11 класс

Урок №38. Определение комплексного числа. Действия с комплексными числами.

Перечень вопросов, рассматриваемых в теме

1) понятие мнимой единицы;

2) определение комплексного числа;

3) действия с комплексными числами и действия над ними.

Запись комплексного числа в виде a + bi называют алгебраической формой комплексного числа, где а – действительная часть, bi – мнимая часть, причем b – действительное число.

Два комплексных числа z = a + bi и = a – bi, отличающиеся лишь знаком мнимой части, называются сопряженными.

Определение. Вычесть из комплексного числа z₁ комплексное число z₂, значит найти такое комплексное число z,

Теорема. Разность комплексных чисел существует и притом единственная.

Определение. Произведением комплексных чисел z₁=a₁+ b₁ i и z₂=a₂+b₂ i называется комплексное число z, определяемое равенством:

Определение. Разделить комплексное число z₁ на комплексное число z₂, значит найти такое комплексное число z, что z · z₂ = z₁.

Теорема. Частное комплексных чисел существует и единственно, если z₂ ≠ 0 + 0i.

Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.

Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2017.

Теоретический материал для самостоятельного изучения

Исходя из этого, получим следующее определение комплексного числа.

б) Сложение комплексных чисел определяется правилом:

в) Умножение комплексных чисел определяется правилом:

Запись комплексного числа в виде a + bi называют алгебраической формой комплексного числа, где а – действительная часть, bi – мнимая часть, причем b – действительное число.

Комплексное число a + bi считается равным нулю, если его действительная и мнимая части равны нулю: a = b = 0

Комплексное число a + bi при b = 0 считается совпадающим с действительным числом a: a + 0i = a.

Комплексное число a + bi при a = 0 называется чисто мнимым и обозначается bi: 0 + bi = bi.

Два комплексных числа z = a + bi и = a – bi, отличающиеся лишь знаком мнимой части, называются сопряженными.

Над комплексными числами в алгебраической форме можно выполнять следующие действия.

Сложение комплексных чисел обладает следующими свойствами:

3º. Комплексное число – a – bi называется противоположным комплексному числу z = a + bi. Комплексное число, противоположное комплексному числу z, обозначается -z. Сумма комплексных чисел z и -z равна нулю: z + (-z) = 0

Пример 1. Выполните сложение (3 – i) + (-1 + 2i).

(3 – i) + (-1 + 2i) = (3 + (-1)) + (-1 + 2) i = 2 + 1i.

Определение. Вычесть из комплексного числа z₁ комплексное число z₂, значит найти такое комплексное число z, что z + z₂ =z₁.

Теорема. Разность комплексных чисел существует и притом единственная.

Определение. Произведением комплексных чисел z₁=a₁+ b₁ i и z₂=a₂+b₂i называется комплексное число z, определяемое равенством:

Умножение комплексных чисел обладает следующими свойствами:

3º. Дистрибутивность умножения относительно сложения:

На практике умножение комплексных чисел производят по правилу умножения суммы на сумму и выделения действительной и мнимой части.

В следующем примере рассмотрим умножение комплексных чисел двумя способами: по правилу и умножением суммы на сумму.

Пример 3. Выполните умножение (2 + 3i) (5 – 7i).

1 способ. (2 + 3i) (5 – 7i) = (2⋅ 5 – 3⋅ (- 7)) + (2⋅ (- 7) + 3⋅ 5)i =

= (10 + 21) + (- 14 + 15)i = 31 + i.

2 способ. (2 + 3i) (5 – 7i) = 2⋅ 5 + 2⋅ (- 7i) + 3i⋅ 5 + 3i⋅ (- 7i) =

= 10 – 14i + 15i + 21 = 31 + i.

Определение. Разделить комплексное число z₁ на комплексное число z₂, значит найти такое комплексное число z, что z · z₂ = z₁.

Теорема. Частное комплексных чисел существует и единственно, если z₂ ≠ 0 + 0i.

На практике частное комплексных чисел находят путем умножения числителя и знаменателя на число, сопряженное знаменателю.

Пусть z₁ = a₁ + b₁i, z₂ = a₂ + b₂i, тогда

В следующем примере выполним деление по формуле и правилу умножения на число, сопряженное знаменателю.

Пример 4. Найти частное

5) Возведение в целую положительную степень.

а) Степени мнимой единицы.

i 8 = i 6 i 2 = 1 и т. д.

Поэтому, чтобы возвести число i в целую положительную степень, надо показатель степени разделить на 4 и возвести i в степень, показатель которой равен остатку от деления.

i 36 = (i 4 ) 9 = 1 9 = 1,

i 17 = i 4⋅ 4+1 = (i 4 ) 4 ⋅ i = 1 · i = i.

б) Возведение комплексного числа в целую положительную степень производится по правилу возведения двучлена в соответствующую степень, так как оно представляет собой частный случай умножения одинаковых комплексных сомножителей.

Пример 6. Вычислите: (4 + 2i) 3

(4 + 2i) 3 = 4 3 + 3⋅ 4 2 ⋅ 2i + 3⋅ 4⋅ (2i) 2 + (2i) 3 = 64 + 96i – 48 – 8i = 16 + 88i.

Стоит отметить. что с помощью комплексных чисел можно решать квадратные уравнения, у которых отрицательный дискриминант.

Рассмотрим решение квадратных уравнений, дискриминант которых отрицателен.

Пример 7. Решите уравнения:

а) x 2 – 6x + 13 = 0; б) 9x 2 + 12x + 29 = 0.

Решение. а) Найдем дискриминант по формуле
D = b 2 – 4ac.

Так как a = 1, b = – 6, c = 13, то
D = (– 6) 2 – 4×1×13 = 36 – 52 = – 16;

Корни уравнения находим по формулам

б) Здесь a = 9, b = 12, c = 29. Следовательно,
D = b 2 – 4ac =122 – 4×9×29 = 144 – 1044 = – 900,

Находим корни уравнения:

Мы видим, что если дискриминант квадратного уравнения отрицателен, то квадратное уравнение имеет два сопряженных комплексных корня.

Разбор решения заданий тренировочного модуля

№1. Тип задания: единичный выбор

Вычислите сумму (2 + 3i)+ (5 – 7i).

Можем сделать вывод, что верный ответ

№2. Тип задания: ввод с клавиатуры пропущенных элементов в тексте.

Источник

Выполнить действия над комплексными числами в тригонометрической форме

где x и y – действительные числа, а i так называемая мнимая единица. Соотношение для мнимой единицы

Понятия «больше» и «меньше» для комплексных чисел не вводятся.

Числа z = x + iy и называются комплексно сопряженными.

Алгебраической формой комплексного числа называется з апись числа z в виде z = x + iy.

Модуль r и аргумент φ можно рассматривать как полярные координаты вектора , изображающего комплексное число z = x + iy (см. рис. 7.1). Тогда из соотно­шений сторон в прямоугольном треугольнике получа­ем

Равенство (7.3) есть тригонометрическая форма комплексного числа. Модуль r = |z| однозначно определяется по формуле

Аргумент определяется из формул:

Используя формулу Эйлера

комплексное число можно записать в так назы­ваемой показательной (или экспоненциальной) форме

где r =| z | — модуль комплексного числа, а угол ( k =0;–1;1;–2;2…).

Пример 7.1. Записать комплексные числа в тригонометрической и показательной формах.

На множестве комплексны х чисел определен ряд операций.

Из (7.11) следует важнейшее соотношение i 2 = –1. Действительно,

Видно, что при умножении комплексных чисел в тригонометрической форме их модули перемножаются, а аргументы складываются. Это правило распространяется на любое конечное число множителей. Нетрудно видеть, что если есть n множителей и все они одинаковые, то частным случаем равенства (7.12) является формула возведения комплексного числа в натуральную степень:

(7.13) называется первой формулой Муавра.

Произведение двух комплексных чисел в показательной (экспоненциальной) форме имеет вид:

На практике при нахождении частного двух комплексных чисел удобно умножить числитель и знаменатель дроби на число, сопряженное знаменателю, с дальнейшим применением равенства i 2 = –1 и формулы разности квадратов.

Деление комплексных чисел осуществляется также и в тригонометрической форме, при этом имеет место формула:

Видно, что при делении комплексных чисел их модули делятся, а аргументы вычитаются соответственно.

Частное двух комплексных чисел в показательной (экспоненциальной) форме имеет вид:

Пользуясь формулой (7.11), вычислим их произведение

На основании формулы (7.14) вычислим их частное

Решение. Используя (7.4) и (7.5), получаем:

Аналогично, для z ₂ можно записать:

По формулам (7.12) и (7.16) получим в тригонометрической форме:

Пользуясь формулами (7.14) и (7.17), получим в показательной форме:

в натуральную степень, определенному ранее формулой (7.13).

(7.18) называется второй формулой Муавра.

Пример 7.4. Найти все корни уравнения z 4 +16=0.

Теорема 7.1 (основная теорема алгебры). Для всякого многочлена с комплексными коэффициентами

Приведем еще одну теорему, имеющую место над множеством комплексных чисел.

Таким образом, произведение линейных множителей, соответствующих сопряженным корням, можно заменить квадратным трехчленом с действительными коэффициентами, а соответствующее квадратное уравнение будет иметь отрицательный дискриминант.

Источник

Действия над комплексными числами в тригонометрической форме (для ДО)

Тема: « Действия над комплексными числами в тригонометрической форме»

1. Актуализация ранее полученных знаний и умений.

Сначала повторим то, что уже было изучено ранее, вспомним ещё раз как геометрически изображаются комплексные числа (далее буду писать к.ч.), как выполняются операции над к.ч. в алгебраической форме (см. предыдущий конспект к уроку). Все задания записывайте в рабочую тетрадь!

Задание№2. Выполнить сложение к.ч. ,

Решение: Для того чтобы сложить два комплексных числа нужно сложить их действительные и мнимые части:

Задание №3.Найти разности к.ч. и , если ,

Решение: Действие аналогично сложению, единственная особенность состоит в том, что вычитаемое нужно взять в скобки, а затем – стандартно раскрыть эти скобки со сменой знака:

, т.е. можно записать в виде .

Рассчитаем вторую разность: .

Задание №4. Найти произведение комплексных чисел ,

Решение: Очевидно, что произведение следует записать так: , главное, помнить, что и быть внимательным.

Это и есть ответ.

!Надеюсь, всем было понятно, что

! В учебной литературе и на просторах Сети легко найти специальную формулу для вычисления произведения комплексных чисел. Если хотите, пользуйтесь, но мне кажется, что подход с умножением многочленов универсальнее и понятнее. Формулу приводить не буду, считаю, что в данном случае – это забивание головы опилками.

2. Далее, перейдем к рассмотрению новой темы. На прошлом уроке, мы уже записали тригонометрическую форму к.ч. Рекомендую посмотреть видео-урок (5мин) «Тригонометрическая запись комплексного числа», перейдя по ссылке https://www.youtube.com/watch?v=ORr7P-sNJqc (в тетрадь можно не записывать видео-урок).

3. Сформулируем основные формулы для выполнения действий над к.ч. в тригонометрической форме. Весь ниже изложенный материал запишите в рабочую тетрадь. (это можно сделать в виде памятки)

Памятка№1

Рассмотрим примеры перехода к.ч. изалгебраической в тригонометрическую форму (записать в рабочую тетрадь)

3.1.Представить в тригонометрической форме комплексные числа: , , , .

Решение:

Найдем его модуль и аргумент. . Поскольку (случай 1 (см. видео-урок)), то . Таким образом: – число в тригонометрической форме.

2. Представим в тригонометрической форме число .

Найдем его модуль и аргумент Поскольку (случай 2), то – вот здесь нечетностью арктангенса воспользоваться нужно. К сожалению, в таблице отсутствует значение , поэтому в подобных случаях аргумент приходится оставлять в громоздком виде: – число в тригонометрической форме.

3. Представим в тригонометрической форме число .

Найдем его модуль и аргумент. . Поскольку (случай 3), то .

Таким образом: – число в тригонометрической форме.

4. Представим в тригонометрической форме число .

Найдем его модуль и аргумент.

Поскольку (случай 1), то (минус 60 градусов).

Таким образом: – число в тригонометрической форме.

!А вот здесь, минусы не трогаем.

Любое комплексное число (кроме нуля) можно записать в показательной форме: , где – это модуль комплексного числа, а – аргумент комплексного числа.

Что нужно сделать, чтобы представить комплексное число в показательной форме? Почти то же самое: найти модуль и аргумент. И записать число в виде .

Памятка№2 (как представить к.ч. в показательной форме)

Рассмотрим пример записи к.ч. в показательной форме.

Например, для числа предыдущего примера у нас найден модуль и аргумент: , . Тогда данное число в показательной форме запишется следующим образом: z_{2 =}2√5×e i (П- arctg 2) .

Например, число в показательной форме будет выглядеть так: z₄=2×e i (-П/3)

Например, число в показательной форме будет записываться так: z₁=2√3×e i П/6

Сделаем вывод, что комплексное число в показательной форме записывается строго по форме .

Памятка№3 (как возвести к.ч. в степень)

Рассмотри примеры возведения комплексных чисел в степень

а) возвести в степень комплексные числа , ,

Решение: Здесь тоже всё просто, главное, помнить знаменитое равенство:

Если же, мнимая единица возводится в нечетную степень, то «отщипываем» одно «и», получая четную степень: i 33 = i×i 32 = i×(i 2 ) 16 = i×(-1) 16 = i×1 = i

Источник