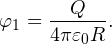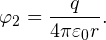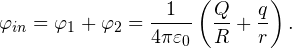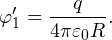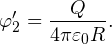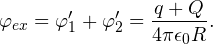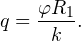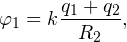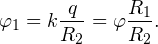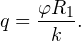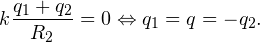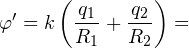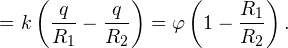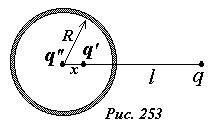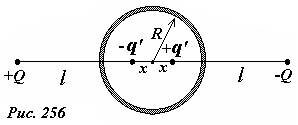заземленная сфера что значит
Заземление проводников
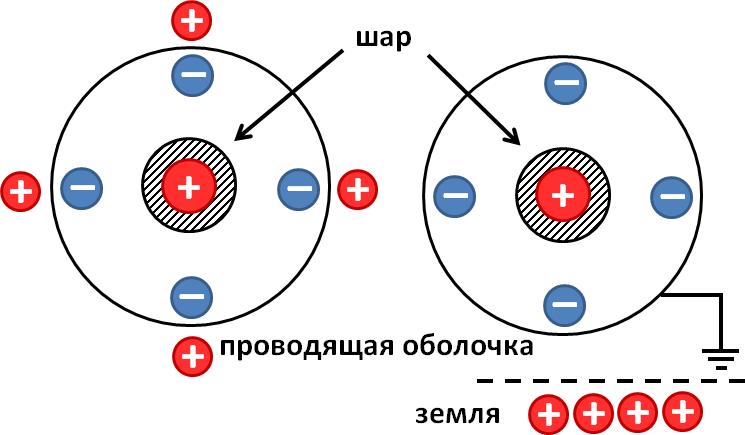
Читатель: Что произойдет, если шар радиуса r, заряженный зарядом q, заземлить, т.е. соединить с поверхностью Земли? Например, соединив шар с трубой парового отопления.
Автор: Все будет происходить так, как если бы мы соединили наш проводник с огромным незаряженным шаром радиуса R >> r. После заземления потенциалы нашего шарика и огромного шара сравняются:
j = 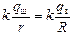
где qш – заряд шарика, а qз – заряд Земли после заземления. Отсюда
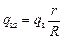
если R ® ¥, а qз + qш = q, то очевидно, что qш ® 0. То есть весь заряд стечет на Землю.
СТОП! Решите самостоятельно: А1, А2.
Читатель: Как с помощью положительно заряженного тела зарядить незаряженный проводник отрицательно, не изменив заряда первого тела?
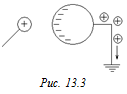
СТОП! Решите самостоятельно: А3, В1, В2, В6.
СТОП! Решите самостоятельно: В4, С10, С11.
Рассмотрим поток вектора 
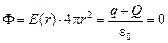
где Q – искомый заряд сферы. Отсюда Q = –q.
Теперь возьмем поток через сферу S2 радиуса r0 0 находится незаряженный проводящий шарик радиуса r0. Шарик заземляют проводом, проходящим через небольшое отверстие в сфере (рис. 13.10). Найти заряд q, который будет на шаре после заземления. Построить график Е(r), нарисовать картину силовых линий и определить потенциал сферы после заземления.
двух незаряженных проводников между ними должно произойти какое-либо перераспределение заряда?
Автор: Потенциал поверхности незаряженного шара в начальный момент равен потенциалу поля, созданного зарядом сферы:
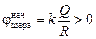
Потенциал же Земли 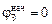
Читатель: А как же найти этот заряд?
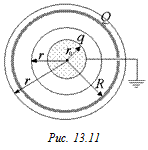
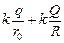
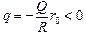
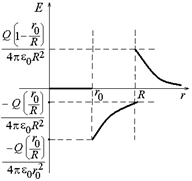
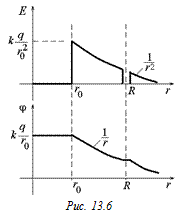
Построим график Е(r). Для этого вычислим поток через сферы радиусом r (рис. 13.11):
1) r0 R, 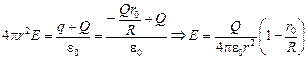
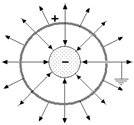
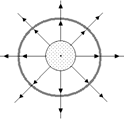
График Е(r) показан на рис. 13.12, а силовые линии – на рис. 13.13.
Потенциал сферы определим как алгебраическую сумму потенциалов полей шара и сферы:
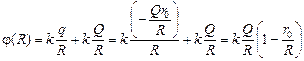
Ответ: 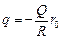
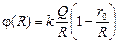
СТОП! Решите самостоятельно: В8, В9, С16, С18.
Примеры решения задач по физике — концентрические проводящие сферы
Среди школьных задач по физике особняком стоят те, которые связаны с концентрическими проводящими сферами. Эти сферы могут быть заряжены, заземлены, могут находиться в поле внешних зарядов и т. д., вариаций много. В школьном курсе физики эти задачи являются одними из самых сложных. Не в последнюю очередь, конечно, непонимание данного материала связано с неспособностью учителей объяснить его грамотно и доступно. Итак, попробуем разобраться, что это за проводящие сферы и с чем их едят.
Тексты заданий я взял из сборника задач по физике для подготовительных отделений вузов.
| Задача 1. Сфера радиуса r, которой сообщен заряд q, окружена концентрической тонкостенной проводящей сферической оболочкой радиуса R, заряд которой равен Q. Определите потенциалы сфер φin (внутренней) и φex (внешней). |
Решение. Потенциал на поверхности внутренней сферы φex складывается из двух потенциалов: внешней сферы φ1 и собственно внутренней сферы φ2.
Потенциал внешней сферы φ1 в каждой точке ее внутреннего объема одинаков и равен потенциалу на ее поверхности (подробнее о решении задач на тему «Потенциал» читайте в этой статье):
Потенциал внутренней сферы φ2 определяется известным соотношением:
Тогда общий потенциал φin на поверхности внутренней сферы равен:
Потенциал на поверхности внешней сферы также складывается из двух потенциалов: внутренней сферы φ’1 и собственно внешней сферы φ’2.
Потенциал внутренней сферы φ’1 на расстоянии R от ее центра определяется известным соотношением:
Формула, определяющая потенциал внешней сферы φ’2 на ее поверхности, также хорошо известна:
Тогда общий потенциал на поверхности внешней сферы равен:
| Задача 2. Металлический шар радиуса R1, заряженный до потенциала φ, окружают тонкой сферической проводящей оболочкой радиуса R2. Определите потенциал шара φ1 после того, как он будет соединен проводником с оболочкой. Первоначальный заряд оболочки равен нулю, центры оболочки и шара совпадают. |
Решение. До соединения сфер проводником заряд первой был равен:
После соединения часть заряда с внутренней сферы перетекло на внешнюю. Ток прекратился в тот момент, когда потенциал шара стал равен потенциалу внешней оболочки. Удобнее поэтому искать не потенциал шара, а равный ему потенциал внешней оболочки. В соответствии с результатами, полученными в предыдущей задаче, этот потенциал определяется выражением:
где q1 и q2 — заряды шара и внешней оболочки после соединения их проводником соответственно. По закону сохранения заряда q = q1 + q2. После несложных преобразований получаем:
| Задача 3. Металлический шар радиуса R1, заряженный до потенциала φ, окружают концентрической сферической проводящей оболочкой радиуса R2. Чему станет равен потенциал шара φ‘, если заземлить оболочку? |
Начнем с рисунка к решению задачи:
После заземления проводящей оболочки весь положительный заряд, образовавшийся на ней вследствие явления электростатической индукции, стекает на землю. На ней остается только отрицательный заряд, поскольку он притягивается к положительному заряду внутренней сферы
Решение. Зная потенциал шара в начальный момент времени и его радиус, можно найти заряд на нем:
Вследствие явления электростатической индукции на внешней оболочке должно произойти разделение заряда. Отрицательный заряд перетечет на внутреннюю поверхность оболочки, положительный — на внешнюю (см. рисунок). Это же явление возникало и в предыдущих задачах, но мы не принимали его во внимание. Почему? В условии задач было указано, что оболочка тонкая, и такое «разбегание» зарядов не приводило к сколько-нибудь существенному изменению конфигурации электростатического поля.
В этой задаче учет данного явления важен, поскольку оболочку заземляют. После заземления положительный заряд с оболочки стечет на землю, останется лишь отрицательный q2, поскольку он притягивается к положительному заряду q1 внутренней сферы. Потенциал заземленной оболочки станет равен потенциалу земли, то есть нулю. В этой связи и в соответствии с результатом, полученным при решении первой задачи, получаем равенство:
Используя выражение для расчета потенциала внутренней сферы подобной системы, полученное в первой задаче, находим окончательно требуемый потенциал шара:
Опыт показывает, что редко кто понимает решение этих задач во всех деталях с первого раза. Обычно приходится долго и настойчиво разъяснять ученикам все те мелочи, без осознания которых решение сводится к пустым преобразованиям буквенных выражений с целью получения приведенного в конце учебника ответа. Понять физическую сущность этих задач и научиться применять полученные знания в будущем не просто. Однако в этом и состоит основная методическая ценность данной темы в школьном курсе физики. Лучшим помощником в ее изучении непременно станет профессиональный репетитор, грамотный наставник, который сможет придумать понятное именно вам объяснение и ответит на все возникшие вопросы. Кстати, если таковые имеются, вы можете задать их ниже в комментариях.
Учебники
Журнал «Квант»
Общие
§10. Проводники и диэлектрики в электростатическом поле
10.4 Расчет поля в присутствии проводников. Метод изображений.
Мы уже подчеркивали, что основная проблема расчета полей в присутствии проводников заключается в появлении индуцированных зарядов, распределение которых заранее не известно. В связи с этим рассмотренные ранее методы, основанные на законе Кулона и принципе суперпозиции, в данном случае оказываются непригодными. Принципиально иной подход к решению данной задачи заключается в расчете распределения потенциала электростатического поля. Действительно, на поверхности проводника распределение заряда не известно, но ведь потенциал проводника постоянен!
Сам метод основан на решении уравнений [1] для потенциала поля. Сами эти уравнения довольно сложны и рассматриваются в курсе физики высшей школы, однако, их физический смысл основывается на законе Кулона и связи потенциала с напряженностью поля.
Однако в некоторых случаях можно рассчитать электрическое поле и распределение индуцированных на поверхности проводника зарядов, используя искусственный прием, который называется метод изображений.
Изложим кратко суть и дадим обоснование этого метода.
Пусть в некоторой области пространства V, ограниченной поверхностью S (в частном случае граница области может простираться до бесконечности), задано распределение зарядов qi (рис. 242).
Электрическое поле в выделенной области определяется однозначно, если
Заметим, что на границе области могут существовать заряды, однако даже при неизвестном их распределении, задание потенциала на границе однозначно определяет поле внутри области. Поэтому две различные задачи, но с одинаковыми распределениями зарядов внутри области и одинаковыми потенциалами на границе имеют внутри области одинаковые решения. Иногда при неизвестном распределении индуцированных зарядов на границе удается подобрать такое распределение зарядов вне рассматриваемой области, что для нового распределения выполненяются граничные условия исходной задачи. В этом случае дополнительные заряды называются зарядами-изображениями. Поиск изображений имеет смысл вести тогда, когда новая задача оказывается проще исходной и имеет простое решение.
Помимо задания распределения потенциала, в качестве граничных условий могут использоваться и некоторые другие, например, значение напряженности поля. Формулировке граничных условий, по этой причине уделяется серьезное внимание в курсе электродинамики.
Точечный заряд над плоской проводящей поверхностью.
Рассмотрим простейшую задачу, допускающую решение с помощью метода изображений.
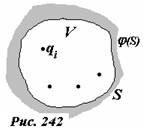
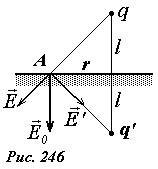
Пусть точечный заряд +q0 находится на расстоянии l от бесконечной металлической пластины (рис. 243).
Очередной раз мы пользуемся моделями – в данном случае под бесконечной, понимается пластина, размеры которой значительно больше расстояния до заряда. Кроме того, можно считать, что пластина заземлена, так как она «касается бесконечности».
Под действием электрического поля заряда +q0 электроны пластины придут в движения и начнут скапливаться под точечным зарядом, создавая отрицательный индуцированный заряд.
Если пластина реально заземлена, то эти заряды натекут из заземления. На большой незаземленной пластине возникнут положительные заряды на краях пластины, но так как эти края находятся далеко, то их полем в рассматриваемой области можно пренебречь.
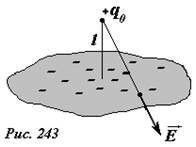
Распределение поверхностной плотности индуцированных зарядов на пластине σ не известно, но известно, что ее потенциал постоянен и равен нулю.
Сравним данную простую задачу (два точечных заряда) с исходной (точечный заряд и индуцированные им заряды σ на проводящей пластине): в полупространстве над пластиной распределения зарядов одинаковы (в обоих случаях – один точечный заряд), на граничной плоскости потенциалы равны; следовательно, в этом полупространстве электрические поля также одинаковы.
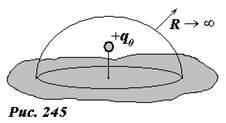
Строго говоря, мы должны рассматривать замкнутую область пространства, поэтому мысленно накроем заряд +q0 полусферой, опирающейся на плоскость, положим ее потенциал равным нулю и устремим ее радиус к бесконечности, и таким образом придем к рассматриваемому полупространству (рис. 245).
Напряженность суммарного поля у границы \(
\vec E_0\) можно рассчитать по принципу суперпозиции как сумму полей, создаваемых исходным зарядом \(
\vec E\)и его изображением \(
Суммарный вектор направлен перпендикулярно границе и равен
Сила притяжения заряда к пластине определяется полем, создаваемым индуцированными зарядами, которое в свою очередь эквивалентно полю заряда изображения, поэтому равно силе взаимодействия двух точечных зарядов q и q’
Этот вывод можно пояснить следующим образом: при двух реальных точечных зарядах при перемещении одного из них второй остается неподвижным. Если же уносить заряд от проводящей границы, то его изображение также удаляется, поэтому совершаемая работа будет меньше.
Картина силовых линий также может быть рассчитана, как поле двух точечных зарядов (рис. 247). Обратите внимание, что во всех точках плоскости силовые линии перпендикулярны поверхности.
Продолжим развитие идей построения зарядов-изображений.
Совершенно аналогично можно построить поле заряда, помещенного на биссектрису двугранного угла, величина которого целое число раз укладывается в полном угле, например, в угле 60°. Шесть зарядов, знаки которых чередуются, расположенных в вершинах правильного шестиугольника, обеспечивают равенство нулю потенциала на гранях угла.
Изображение заряда в сфере.
Прежде, чем приступить к рассмотрению следующей группы задач, связанных с описанием взаимодействия точечного заряда и проводящей сферы, решим одну вспомогательную задачу.
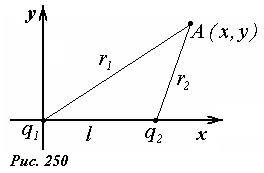
Пусть электростатическое поле создается двумя точечными зарядами, находящимися на расстоянии l друг от друга. Величины и знаки зарядов различны и равны q1 и q2. Покажем, что поверхность нулевого потенциала этого поля представляет собой сферу.
Выберем систему координат, так чтобы заряд q1 находился в начале координат, а заряд q2 на оси Ox (рис. 250). Так задача обладает осевой симметрией, то достаточно показать, что в плоскости xOy линия нулевого потенциала является окружностью. Запишем выражение для потенциала электростатического поля в произвольной точке A с координатами (x,y)
Полагая φ = 0, получим уравнение, определяющее линию нулевого потенциала. Обозначим \(
А это есть уравнение окружности радиуса \(
Итак, запомним – в поле создаваемом двумя точечными зарядами разными по знаку и величине, поверхность нулевого потенциала представляет собой сферу.
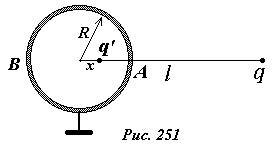
Рассмотрим теперь такую систему: точечный заряд q расположен на расстоянии l от центра металлической заземленной сферы радиуса R. Исследуем электрическое поле в этом случае.
На поверхности металлической заземленной сферы возникнут индуцированные заряды, распределение которых заранее не известно, однако потенциал сферы равен нулю. Мы показали, что поле двух точечных зарядов имеет в качестве поверхности нулевого потенциала сферу. Теперь мы можем использовать этот результат.
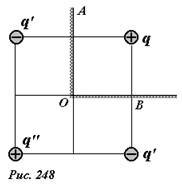
Для определения величины заряда-изображения q’ и его положения можно потребовать выполнения условия φ = 0 в двух точках сферы, например, A и B (рис. 251):
Решив эту систему относительно неизвестных q’ и x, получим
Для определения суммарного индуцированного заряда воспользуемся теоремой Гаусса. Окружим сферу замкнутой поверхностью. По теореме Гаусса, поток вектора напряженности электрического поля через эту поверхность равен суммарному заряду внутри поверхности, деленному на ε0. Так поле индуцированных зарядов эквивалентно полю заряда изображения, то и суммарный индуцированный заряд равен величине заряда-изображения \(
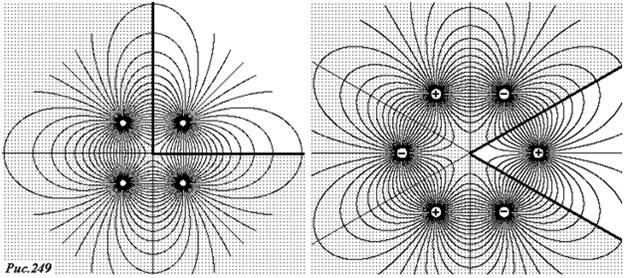
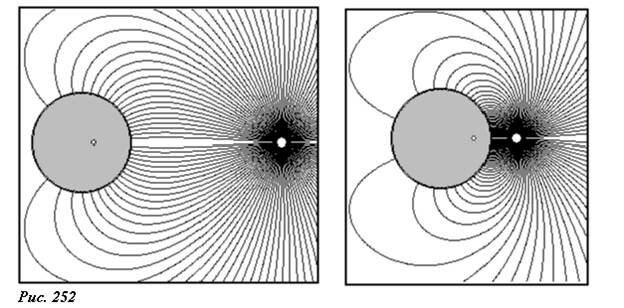
На рисунке 252 показаны силовые линии поля, при двух различных значениях расстояниях до точечного заряда. Обратите внимание, что при увеличении расстояния между зарядом и сферой искажения поля точечного заряда уменьшаются. Как всегда, у поверхности проводника силовые линии перпендикулярны границе, что соответствует условию равновесия индуцированных зарядов на поверхности проводника.
Силу взаимодействия между сферой и точечным зарядом можно найти как силу взаимодействия между двумя точечными зарядами q, q’ :
Заметим, что при l >> R сила взаимодействия становится равной
Итак, вне сферы поле, создаваемое точечным зарядом q и индуцированными зарядами на поверхности, эквивалентно полю трех точечных зарядов q, q’, q’’.
Обратите внимание, число зарядов изображений определяется только необходимостью выполнения граничных условий.
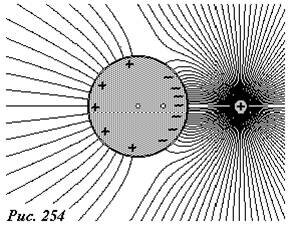
На рисунке 254 показана картина силовых линий электрического поля рассматриваемой системы зарядов. Обратите внимание, что имеются силовые линии, начинающиеся на положительных зарядах сферы. Незаземленная сфера гораздо меньше возмущает поле точечного заряда, чем заземленная. Действительно, на ней происходит только перераспределение зарядов.
Сила, действующая на заряд q, вычисляется как сумма сил, действующих со стороны двух изображений
При l >> R сила взаимодействия
убывает обратно пропорционально пятой степени расстояния, что также легко объяснимо: величина индуцированного дипольного момента пропорциональна величине внешнего поля (которое убывает обратно пропорционально квадрату расстояния), а величина поля диполя убывает обратно пропорционально кубу расстояния.
Заметим, что в данном случае можно вычислить потенциал сферы, не рассчитывая распределения зарядов на поверхности. По принципу суперпозиции, потенциал центра сферы равен сумме потенциалов заряда q и индуцированных зарядов на поверхности сферы. Все индуцированные заряды находятся на одном и том же расстоянии от центра и их сумма равна нулю, следовательно, равен нулю и потенциал, создаваемый ими в центре сферы. Поэтому потенциал в центре сферы, следовательно, и в любой ее точке, равен потенциалу поля точечного заряда \(
Суммарный заряд сферы остается равным нулю, но сфера приобретает индуцированный дипольный момент, который равен дипольному моменту двух зарядов-изображений
Перепишем эту формулу в виде
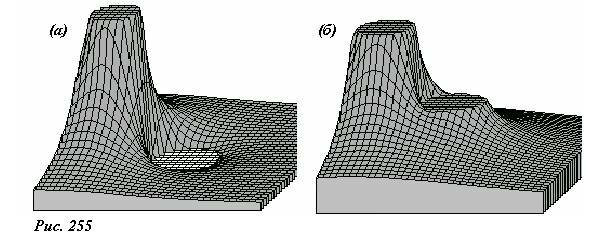
Достаточно интересно рассмотреть распределение потенциала в плоскости, проходящей через точечный заряд и центр сферы. Эти потенциальные функции для заземленной (а) и незаземленной (б) сфер изображены на рисунке 255. Функция, описывающая потенциал поля, вне сферы совпадает с потенциалом поля точечных зарядов (исходного и изображений), а внутри сферы равна нулю в случае (а) и постоянна в случае (б) – круглые горизонтальные площадки совпадает с сечением сферы. Резкое «возвышение» есть потенциал поля точечного заряда, который стремится к бесконечности, здесь, как и на других рисунках, он «обрезан».
Проводящий шар в однородном поле.
x = \frac
При увеличении расстояния между зарядами поле в области шара становится практически однородным с напряженностью
Выразим индуцированный дипольный момент шара через напряженность поля
как видите, этот дипольный момент не зависит от «придуманных» зарядов Q и расстояния l, поэтому и в однородном поле шар будет иметь такой же дипольный момент. Обратите внимание, что и в данном случае поляризуемость шара равна его утроенному объему.
Таким образом, поле индуцированных на поверхности шара зарядов эквивалентно полю точечного диполя, находящегося в центре шара. Картину силовых линий такого поля мы уже использовали ранее.
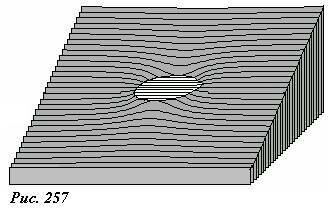
Неплохо также смотрится и распределение потенциала (рис. 257).
Заметим, что потенциал однородного поля изменяется по линейному закону, поэтому распределение потенциала в таком поле изображается наклонной плоскостью. При помещении в это поле проводящего шара на наклонной плоскости появляется горизонтальная площадка, постоянного потенциала на проводнике.
Задание для самостоятельной работы.