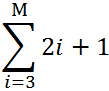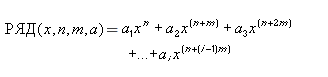знак суммы что означает

Что такое сумма в математике 1 класс?

Математика (1 класс)/Прибавление чисел

Слагаемые — это два числа, которые прибавляются друг к другу. В результате чего получается их сумма. … Здесь, например число 2 — первое слагаемое (или «левое» слагаемое), а число 1 — второе (или «правое» слагаемое). Число три — их сумма.

Что в математике означает греческая буква сигма?

Обозначения Прописная буква Σ обозначает: в математике — сумму; F-сигма-множество

Как набрать знак суммы на клавиатуре?

Как обозначить сумму?

Сумму математически обозначают заглавной греческой буквой Σ (сигма). где: i — индекс суммирования; ai — переменная, обозначающая каждый член в серии; m — нижняя граница суммирования, n — верхняя граница суммирования.

Что такое сумма чисел 2 класс?

Сложение – это объединение объектов в одно целое. Результатом сложения чисел является число, называемое суммой чисел (слагаемых). Вычитание – это такое действие, в котором отнимают меньшее число от большего. Большее число называется уменьшаемым, меньшее – вычитаемым, результат вычитания – разностью.

Как в ворде поставить знак суммы?

Использование кода для быстрой вставки знака суммы

Что значит слово сумма?

1) Число, получаемое в результате сложения двух или нескольких величин. 2) а) Общее количество чего-л.

Как выглядит Сигма?

СИГМА — (sigma) Буква греческого алфавита; заглавная изображается как Σ, строчная – как σ.

Источник

Что означает знак суммы в формуле

В математике для записи сумм, содержащих много слагаемых, или в случае, когда число слагаемых обозначено буквой, применяется следующая запись:

которая расшифровывается так

(14.1)

где — функция целочисленного аргумента. Здесь символ (большая греческая буква «сигма») означает суммирование. Запись внизу символа суммирования показывает, что переменная, которая меняет свои значения от слагаемого к слагаемому, обозначена буквой и что начальное значение этой переменной равно . Запись вверху обозначает последнее значение, которое принимает переменная .

Пример 14.2 Вычислим несколько сумм:

1) .

2) . Так как в правой части стоит сумма геометрической прогрессии с первым членом равным и знаменателем прогрессии равным , то эту сумму легко найти

3) .

4) .

5) .

В курсе линейной алгебры чаще всего будут встречаться суммы вида . Здесь переменная с индексом рассматривается как функция от своего индекса. Поэтому

С помощью знака суммы формулу (10.1) скалярного произведения векторов можно записать так:

(14.2)

где для трехмерного пространства , для плоскости .

Для единообразия будем считать, что

и говорить, что это сумма, содержащая одно слагаемое.

Замечание 14.1 Буква, стоящая внизу под знаком суммы (индекс суммирования), не влияет на результат суммирования. Важно лишь, как от этого индекса зависит суммируемая величина. Например,

в правой части никакой буквы нет, значит, и результат от не зависит.

Предложение 14.1 Множитель, не зависящий от индекса суммирования, может быть вынесен за знак суммы:

Доказательство этого предложения предоставляется читателю.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: При сдаче лабораторной работы, студент делает вид, что все знает; преподаватель делает вид, что верит ему. 9315 — | 7289 — или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Числовой ряд является некой последовательностью, которая рассматривается совместно с другой последовательностью (ее еще называют последовательностью частичных сумм). Подобные понятия применяются в математическом и комплексном анализе.

Сумму числового ряда можно легко вычислить в Excel с помощью функции РЯД.СУММ. Рассмотрим на примере, как работает данная функция, а после построим график функций. Научимся применять числовой ряд на практике при подсчете роста капитала. Но для начала немного теории.

Сумма числового ряда

Числовой ряд можно рассматривать как систему приближений к числам. Для его обозначения применяют формулу:

Здесь показана начальная последовательность чисел ряда и правило суммирования:

Запись 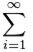обозначает: суммируются натуральные числа от 1 до «плюс бесконечности». Так как _i = 1, то подсчет суммы начинается с единицы. Если бы здесь стояло другое число (например, 2, 3), то суммировать мы начинали бы с него (с 2, 3).

В соответствии с переменной _i ряд можно записать развернуто:

= а₁ + а₂ + а₃ + а₄ + а₅ + … (до «плюс бесконечности).

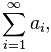
Определение суммы числового ряда дается через «частичные суммы». В математике они обозначаются Sn. Распишем наш числовой ряд в виде частичных сумм:

Сумма числового ряда – это предел частичных сумм S_n. Если предел конечен, говорят о «сходящемся» ряде. Бесконечен – о «расходящемся».

Сначала найдем сумму числового ряда:

Теперь построим в Excel таблицу значений членов ряда:

Общий первый аргумент берем из формулы: i=3.

Все следующие значения _i находим по формуле: =B4+$B$1. Ставим курсор в нижний правый угол ячейки В5 и размножаем формулу.

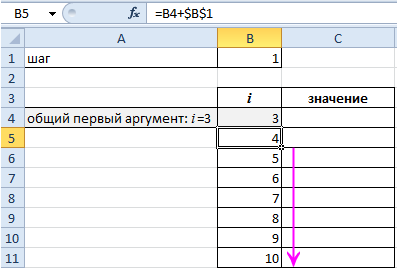
Найдем значения. Делаем активной ячейку С4 и вводим формулу: =СУММ(2*B4+1). Копируем ячейку С4 на заданный диапазон.

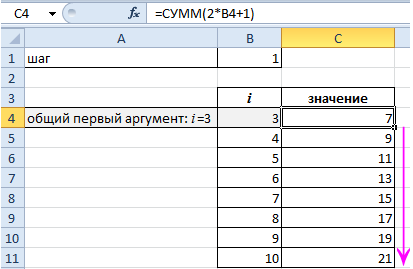
Значение суммы аргументов получаем с помощью функции: =СУММ(C4:C11). Комбинация горячих клавиш ALT+«+» (плюс на клавиатуре).

Функция РЯД.СУММ в Excel

Для нахождения суммы числового ряда в Excel применяется математическая функция РЯД.СУММ. Программой используется следующая формула:

Важные условия для работоспособности функции:

Вычисление суммы ряда в Excel

Та же функция РЯД.СУММ работает со степенными рядами (одним из вариантов функциональных рядов). В отличие от числовых, их аргументы являются функциями.

Функциональные ряды часто используются в финансово-экономической сфере. Можно сказать, это их прикладная область.

Например, положили в банк определенную сумму денег (а) на определенный период (n). Имеем ежегодную выплату х процентов. Для расчета наращенной суммы на конец первого периода используется формула:

На конец второго и последующих периодов – вид выражений следующий:

S₂ = a (1 + x) 2 ; S₃ = a (1 + x) 2 и т.д.

Чтобы найти общую сумму:

S_n = a (1 + x) + a (1 + x) 2 + a (1 + x) 3 + … + a (1 + x) n

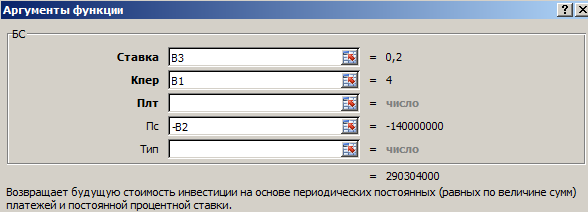
Частичные суммы в Excel можно найти с помощью функции БС().

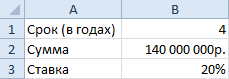
Исходные параметры для учебной задачи:

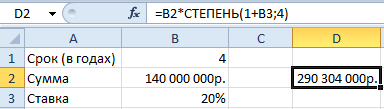
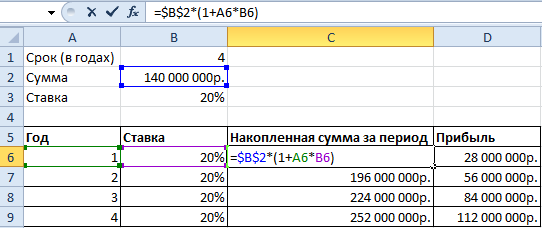
Используя стандартную математическую функцию, найдем накопленную сумму в конце срока сумму. Для этого в ячейке D2 используем формулу: =B2*СТЕПЕНЬ(1+B3;4)

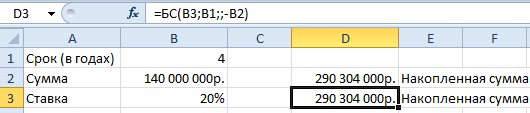
Теперь в ячейке D3 решим эту же задачу с помощью встроенной функции Excel: =БС(B3;B1;;-B2)

Результаты одинаковые, как и должно быть.

Как заполнить аргументы функции БС():

Таким образом, функция БС помогла найти нам сумму функционального ряда.

В Excel есть и другие встроенные функции для нахождения разных параметров. Обычно это функции для работы с инвестиционными проектами, ценными бумагами и амортизационными платежами.

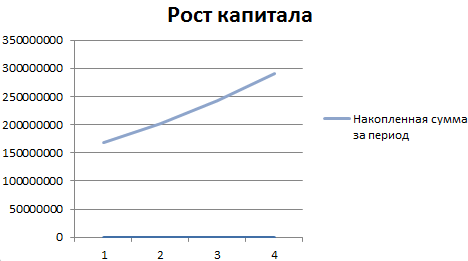
Построение графика функций суммы числового ряда

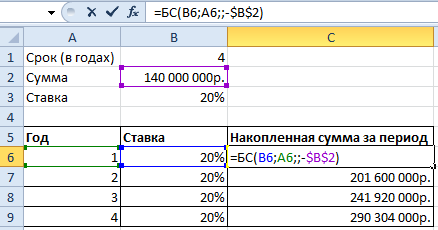
Построим график функций, отражающий рост капитала. Для этого нам нужно построить график функции являющейся суммой построенного ряда. За пример, возьмем те же данные по вкладу:

Дальше нам нужна функция для начисления сложных процентов — БС(). Мы узнаем будущею стоимость инвестиций при условии равных платежей и постоянной процентной ставке. Используя функцию БС(), заполним таблицу:

В первой строке показана накопленная сумма через год. Во второй – через два. И так далее.

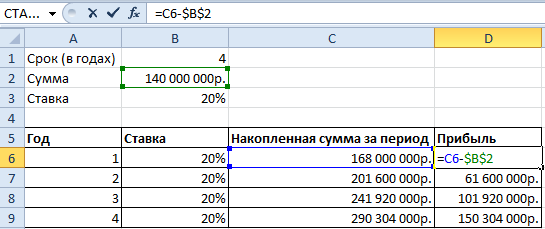
Сделаем еще один столбец, в котором отразим прибыль:

Как мы считали – в строке формул.

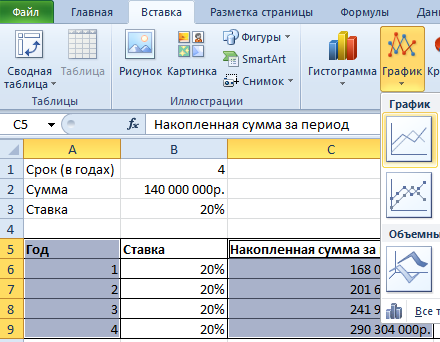
На основании полученных данных построим график функций.

Выделим 2 диапазона: A5:A9 и C5:C9. Переходим на вкладку «Вставка» — инструмент «Диаграммы». Выбираем первый график:

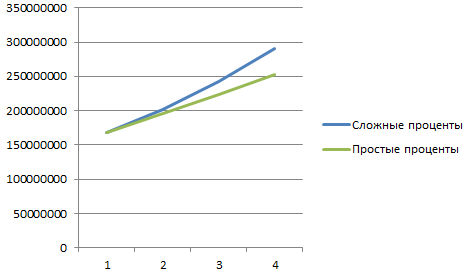
Сделаем задачу еще более «прикладной». В примере мы использовали сложные проценты. Они начисляются на наращенную в предыдущем периоде сумму.

Возьмем для сравнения простые проценты. Формула простых процентов в Excel: =$B$2*(1+A6*B6)

Добавим полученные значения в график «Рост капитала».

Какие именно выводы сделает инвестор – очевидно.

Математическая формула частичной суммы функционального ряда (с простыми процентами): S_n = a (1 + x*n), где а – первоначальная сумма вклада, х – проценты, n – период.

Математика для школьников и студентов, обучение и образование

3. Суммирование

Определение. Пусть дана последовательность чисел и натуральные числа и , причем .

(сумма по от до ) — сумма всех членов последовательности, номера которых не меньше и не больше .

Замечание. Сумма, состоящая из одного слагаемого, считается равной этому слагаемому.

Пример. .

Пример.

Свойства знака

1. .

2. .

3. .

4. .

Пример. Вычислим .

Просуммируем левую и правую части по от до

Слева получаем

Имеем

Задачи.

1. Найти

2.

3.

4.

5.

6. Найти сумму первых членов последовательности, если ее -ый член

7. Найти (пятерок — ).

8. .

Комментариев: 28

1 Vasja_Vasja:

3/2 + 8/3 + 15/4 + 24/5 = (90 + 160 + 225 + 288)/60 = 763/60
Наверное у вас просто опечатка

2 Елизавета Александровна Калинина:

3 Вася Пупкин:

Куб суммы: . Можете просто скобки раскрыть

4 Вася Пупкин:

Это как раз таки понятно, я имел ввиду другое. Не понятно, почему Вы взяли именно куб суммы и как это связано с суммой k^2.

5 Елизавета Александровна Калинина:

Поняла. Это догадка. Логически не объяснить… Искусственный прием. Кто-то, даже не знаю кто, придумал.

6 Вася Пупкин:

Т.е. примеры из данной главы тоже решать основываясь на догадках и интуиции? Меня немного смутил способ, которым я решил первую задачу.

Перебирая всевозможные варианты, я заметил, что сумма последовательности k^3 равна сумме последовательности k, возведенной во вторую степень, т.е. (k(k+1)/2)^2 и доказал это методом мат. индукции.

7 Елизавета Александровна Калинина:

Основываться на догадках и интуиции Вы всегда имеете полное право. В том случае, если Вашу догадку Вы потом строго докажете. То, что Вы написали, является решением. А еще можно было бы рассмотреть

8 Вася Пупкин:

9 Александр:

второй вроде решается с помощью формулы для суммы членов геометрической прогрессии или есть другой способ?

Да, верно. Хорошо бы с выводом формулы

10 Геннадий:

Добрый день!
Все-таки меня учили классически, и ноль для меня всегда целое число, а не натуральное.
Что касается суммы бесконечного числа нулей. Если это сумма вида , т.е. сумма счетного числа нулей, то она равна нулю. Если же мы рассматриваем неопределенность вида , то здесь могут быть разные варианты.

Геннадий Reply:
Май 31st, 2014 at 18:21

Да, советские математики, а затем и российские не считают ноль натуральным числом. Для зарубежных – это не так. Например, французы Бурбаки определяют натуральные числа как мощности конечных множеств. Поэтому у них ноль (мощность пустого множества) тоже натуральное число.
Что касается суммы нулей, мне тоже хочется, чтобы сумма счетного числа нулей была равна нулю. Но посмотрите на эти преобразования:

Получаем неопределенность. И что с этим делать, понятия не имею.

Геннадий Reply:
Май 31st, 2014 at 18:27

Извините, в формуле между 1 и 0 не пропечатался знак умножения, а также многоточие. Может, такой знак сойдет за умножение: .
В пояснениях к набору формул в LaTex не нашел ни знака умножения, ни многоточия.

Ничего страшного. Спасибо, исправила.

Дело в том, что неопределенности можно раскрывать. И в Вашем примере она раскрывается как нуль, поскольку бесконечность – сумма счетного числа единиц.

Геннадий Reply:
Июнь 1st, 2014 at 10:22

Здравствуйте! Спасибо за корректировку моих текстов. Жаль, нет возможности это сделать самому, поскольку в громоздких формулах ошибки практически неизбежны. И не всегда администратор может их исправить, да и незачем нагружать его этим.
Относительно рассматриваемой суммы, конечно, бесконечность бесконечности рознь, и некоторые неопределенности можно раскрывать. Но ноль, все-таки, «он и в Африке ноль». И в данном случае меня «гложет сомнение». Смотрите, что получается:

В итоге мы раскрыли неразрешимую неопределенность. Где-то ошибка, или здесь первое равенство недопустимо, или сумма счетного числа нулей не равна нулю.

Если будет ошибка, пишите, я исправлю.
По поводу неопределенности. Она может быть раскрыта, если известно, какая неопределенность. У Вас с первым равенством все в порядке, второе равенство не всегда является равенством, только для рассматриваемого случая это так.

Геннадий Reply:
Июнь 2nd, 2014 at 0:16

Извините, но Вы меня совсем запутали. Разве равенство 0/0 = 0 может быть верно для какого-то особого случая? На мой взгляд, такое равенство либо всегда верно, либо всегда ложно. И справедливо, конечно, последнее.

Смотрите, — неопределенность. Я имею в виду, скажем, такие соотношения: , , . Все это неопределенности вида . Однако в первом случае предел равен , во втором — , а в третьем — .

11 Геннадий:

Здравствуйте, Елизавета Александровна! Конечно, 0/0 – это неопределенность, и Ваши примеры с пределами доходчиво иллюстрируют роль бесконечно малых различных порядков. Мне хотелось проанализировать неопределенность 0/0 с помощью бесконечно малых и бесконечно больших констант, и здесь помогла статья на Вашем сайте http://hijos.ru/diskussionnyj-klub/analiz-myortv-da-zdravstvuet-analiz/.
Неопределенность 0/0 как деление двух бесконечно малых констант можно свести к сумме счетного числа нулей лишь в том случае, когда в числителе бесконечно малая такого же или большего порядка, чем в знаменателе. Если числитель и знаменатель – бесконечно малые первого порядка, то после преобразования

, заменив далее бесконечность на сумму счетного числа конечных величин и раскрыв скобки, мы в итоге получим бесконечную сумму нулей, а точнее счетное число бесконечно малых первого порядка. Такая сумма равна не нулю, а произвольному конечному числу. Это как разбить конечный отрезок любой длины на бесконечно большое число бесконечно малых частей, т.е. частей нулевой длины, а затем эти части (нули) обратно сложить.
Сумма счетного числа нулей равна нулю, если среди слагаемых нет счетного числа бесконечно малых первого порядка. К такой сумме можно преобразовать неопределенность 0/0, если числитель – бесконечно малая второго и большего порядка, а знаменатель – бесконечно малая первого порядка.
PS. Похоже (или я не прав?), в любой сумме слагаемых может быть конечное число или счетное, но никак не континуум. Знак “+” сам по себе играет роль разделителя суммируемых и, следовательно, подсчитываемых величин, число которых поэтому не более, чем счетно.

Добрый вечер! Если мы разобьем отрезок на части нулевой длины, то таких частей будет не счетное число. Вот тут, например, доказано, что множество вещественных чисел несчетно (теорема 2):http://sernam.ru/lect_math2.php? >

Геннадий Reply:
Июнь 6th, 2014 at 9:52

Здравствуйте, Елизавета Александровна! В прошлом моем комментарии ссылка с ошибкой, повторились кавычки. Если можно, уберите лишнюю кавычку в тексте атрибута href.
Конечно, множество вещественных чисел несчетно, а множество рациональных чисел счетно, но мы не об этом. Если разбивается конечный отрезок вещественной оси на бесконечно большое число бесконечно малых частей, это не значит, что отрезок расщепляется на отдельные точки (наверное, это и невозможно в силу непрерывности).
Процитирую отрывок из того же автора: «бесконечно малая никак и ничем по размеру не отличима от нуля, её размер никак не ощутим и не наблюдаем. Поэтому она точно равна нулю в смысле обычного равенства чисел. Но, тем не менее, бесконечно малая не совпадает с нулём тождественно и в этом смысле равна нулю лишь приближённо».
Мы работаем с бесконечной малой окрестностью конечного числа, в каждой такой окрестности число точек несчетно, но количество самих окрестностей уже счетно. Выделяя окрестности, мы уходим от непрерывности вещественных чисел, уходим от континуума.

12 Меня терзают смутные сомнения:

Нельзя-ли здесь воспользоваться функциональными уравнениями вида

выражению под знаком суммирования?
Рассмотрим приведенный выше пример

Соответствующее функциональное уравнение

Предположим, что решением будет полином 3-й степени.

P.S Проба пера в LaTeX

Проба получилась хорошо
Мне вот только не очень понятно, из чего следует, что нужно так, а не как-нибудь иначе?

Меня терзают смутные сомнения Reply:
Апрель 23rd, 2015 at 5:55

Елизавета Александровна, позвольте сформулировать вопрос по-другому:
Не существует-ли какого-либо стандартного подхода, приема, может-быть трюка, позволяющего решать функциональные уравнения именно этого вида

для большинства ?
Это значительно упростило-бы решение задач на суммирование последовательностей, включая приведенные на этой странице.

Источник