дарси томпсон о росте и форме
СОДЕРЖАНИЕ
Обзор
Книга носит скорее описательный, чем экспериментальный характер: Томпсон не сформулировал свои идеи в форме гипотез, которые можно было бы проверить. Он знал об этом, говоря, что «Эта моя книга не нуждается в предисловии, потому что на самом деле это« все предисловие »от начала до конца».
Редакции
Первое издание вышло в 1917 году в виде единого тома на 793 страницах, опубликованного издательством Cambridge University Press. Второе издание, увеличенное до 1116 страниц, было опубликовано в двух томах в 1942 году. Томпсон написал в предисловии к изданию 1942 года, что он написал «эту книгу в военное время, и ее редакция использовала меня во время другой войны. Это дало мне утешение. и род занятий, когда годы мне запретили служить. Немногое осталось от друзей, которые помогли мне написать это ». Несокращенное издание больше не печатается на английском языке, но издание на 346 страниц было сокращено Джоном Тайлером Боннером и широко публикуется под тем же названием. Книга, часто в сокращенном издании, переиздавалась более 40 раз и была переведена на китайский, французский, немецкий, греческий, итальянский и испанский языки.
СОДЕРЖАНИЕ
Содержание глав первого издания кратко излагается ниже. Все, кроме главы 11, имеют одинаковые названия во втором издании, но многие из них длиннее, о чем свидетельствует нумерация страниц в начале каждой главы. В сокращении Боннера все главы были сокращены, а некоторые полностью удалены, опять же, как указано в начале записи каждой главы ниже.
1. Вступительный
2. О величине
3. Скорость роста
4. О внутренней форме и строении клетки.
5. Формы клеток.
6. Примечание об адсорбции.
Томпсон отмечает, что поверхностное натяжение в живых клетках снижается веществами, напоминающими масла и мыло; там, где их концентрации изменяются локально, это влияет на форму клеток. У зеленой водоросли Pleurocarpus ( Zygnematales ) калий концентрируется вблизи точек роста в клетке.
7. Формы тканей или клеточных агрегатов.
8. То же (продолжение)
9. О конкрементах, спикулах и остистых скелетах.
10. Замечание в скобках по геодезии.
Томпсон применяет использование геодезической линии, «кратчайшего расстояния между двумя точками на поверхности тела вращения», к спиральному утолщению стенок растительных клеток и другим случаям.
11. Логарифмическая спираль [«Равноугольная спираль» во 2-м изд.]
12. Спиральные раковины фораминифер.
13. Формы рогов, зубов или клыков: с примечанием о скручивании.
14. О расположении листьев или филлотаксисе.
Когда каменщик строит заводскую трубу, он кладет свои кирпичи определенным устойчивым, упорядоченным образом, не задумываясь о спиральных узорах, к которым эта упорядоченная последовательность неизбежно ведет, и какие спиральные узоры ни в коем случае не являются «субъективными».
15. О формах яиц и некоторых других полых конструкциях.
16. О форме и механической эффективности
17. О теории преобразований или сравнении родственных форм.
Эпилог
Прием
Современный
«JP McM [urrich]», рецензируя книгу в Science в 1917 году, писал, что «книга является одним из самых убедительных документов в поддержку механистического взгляда на жизнь, который когда-либо был выдвинут», противопоставляя это «витализму». Рецензента интересовало «обсуждение физических факторов, определяющих размер организмов, особенно интересным было рассмотрение условий, которые могут определять минимальный размер».
Эдмунд Майер, рецензируя второе издание The Anatomical Record в 1943 году, отмечал, что «объем книги и общий подход к рассматриваемым проблемам остались неизменными, но были внесены значительные дополнения и переработаны большие части». На него произвело впечатление то, насколько Томпсон следил за развитием многих наук, хотя он считал упоминания о квантовой теории и неопределенности Гейзенберга неразумными.
Это была убедительная демонстрация того, насколько легко можно использовать физические и геометрические принципы, пытаясь понять биологию. Это был большой вклад в 1917 г., когда видные биологи еще защищали витализм. Битва была выиграна настолько, насколько это вообще возможно к моменту издания 1942 года. Книга была несовершенной из-за непонимания Томпсоном эволюции и антипатии к любым концепциям исторической причинности ».
Современный
законы, управляющие размерами организмов и их ростом, статикой и динамикой, действующими в клетках и тканях, включая явления геометрической упаковки, мембран под напряжением, симметрии и деления клеток; а также инженерия и геодезия скелетов простых организмов.
гениальный, чрезвычайно элегантный, очень убедительный и, что немаловажно, нацелен на очень большие особенности организма: архитектуру скелета, изгиб рогов или раковин, очертания организма в целом.
Шализи отмечает простоту Томпсона, объясняя процессы жизни, «используя то немногое, что не знал бы студент-физик-второкурсник (антиредукционистские поклонники Томпсона редко так говорят)». Он отмечает, что Томпсон сознательно избегал ссылки на естественный отбор в качестве объяснения и исключил из своего описания историю, будь то виды или жизнь человека. Он цитирует слова Томпсона «Снежный кристалл сегодня такой же, как когда выпал первый снег»: добавляя «тоже основные силы, действующие на организмы», и комментирует, что мы забыли других ученых начала двадцатого века, которые презирали эволюцию. Напротив, утверждает он,
Томпсон обязан своим постоянным влиянием тому факту, что его альтернатива не вызывает вопросов на каждом шагу. (К тому же, конечно, он писал красиво, лучше поэтов своего времени.)
Это тур де силы, сочетающий классические подходы естественной философии и геометрии с современной биологией и математикой, чтобы понять рост, форму и эволюцию растений и животных.
Богин отмечает, что Томпсон положил начало использованию трансформационных сеток для измерения роста в двух измерениях, но без современных компьютеров этот метод было утомительно применять и нечасто применяли. Тем не менее, книга стимулировала и придавала интеллектуальную ценность новой области исследований роста и развития.
Питер Коутс вспоминает, что
Питер Медавар, как известно, назвал « О росте и форме » «вне всякого сравнения лучшим литературным произведением во всех анналах науки, которое было записано на английском языке».
Коутс, однако, утверждает, что книга выходит далеко за рамки элегантного и влиятельного выражения знаний в форме, «которую могут читать для удовольствия ученые и не ученые»; это по его мнению
Научный писатель Филип Болл отмечает, что
адаптивная сложность, которую мы видим в живом мире, просто не может быть объяснена физикой и химией. Если Д’Арси Томпсон думал иначе, то это могло быть только потому, что он каким-то образом придавал особое значение своим физическим моделям. Возможно, он не был явным виталистом, но определенно чувствуется запах духовных сил в том, что он утверждает.
Влияние
В ознаменование столетия книги « О росте и форме» по всему миру проводится множество мероприятий, включая Нью-Йорк, Амстердам, Сингапур, Лондон, Эдинбург, Сент-Эндрюс и в Данди, где была написана книга. Веб-сайт On Growth and Form 100 был создан в конце 2016 года для отображения всей этой деятельности.
 nature_wonder
nature_wonder
Life Science links
Морфология из математики и физики
[Неоставляемые] попытки объяснить биологические формы с помощью простых правил и законов.
Прошлый век. Д’Арси Томпсон, «О росте и форме».
Любое сколь угодно простое природное явление в реальности состоит из многих компонент, а любое видимое действие и эффект являются результатом бесчисленных соподчиненных действий. Здесь математика являет свою истинную мощь комбинаций и обобщений; к примеру, описание пены или клеточной ткани проводятся с применением математического аппарата именно потому, что эти явления являются суммой более элементарных явлений. Рост и форма всецело обладают комплексной природой, поэтому математические правила необходимы для их описания и интерпретации.
По тем или иным причинам множество живых форм невозможно описать более или менее определенно в математических терминах, потому что существуют затруднения в физике для математиков современности, к примеру, мы никогда не сможем вывести формулу для описания рыбы или черепа. Но мы уже можем использовать математический язык для описания хотя бы в общих чертах формы раковины улитки, завитка рога, контура листа, текстуры ткани, структуры скелета, волшебного кружева крыла насекомого. Даже для этого мы должны научиться у математиков упрощению и обобщению, способности держать в голове типовой случай и забывать про отклонения.
Преобразования одного круга (или сферы) в два круга (или сферы) с точки зрения математики является чрезвычайно сложной трансформацией, а с точки зрения физики это может быть сделано очень просто. Маленькая круглая тыква вырастает в большую округлую или овальную тыкву. Если перетянуть плод посередине, то те же самые силы роста преобразуют круглую структуру в две сообщающиеся сферы. Варьируя положение перетяжки или добавляя новые, можно получить большое разнообразие форм. Ясно, что мы можем объяснять многие обычные биологические процессы развития или изменения формы существованием линий, сдерживающих или определяющих действие сил роста, которые в противном случае были бы однородными и симметричными.
Это очень похоже на действия стеклодува. Стеклодув начинает с трубочки, которую он замыкает с одной стороны, чтобы получить полый пузырек, внутри которого вдуваемый воздух создает равномерное давление на все стенки. Получившаяся сфера, которая создается однородной расширяющей силой, модифицируется в любую другую форму при помощи разделителей, позволяющих стеклодуву неравномерно нагревать или охлаждать разные части пузырька.
Оливер Вендел первым отметил эту любопытную аналогию между действиями стеклодува и природы, которая тоже обычно начинает с полой трубочки. Пищеварительная система, кровеносная система (включая сердце), центральная нервная система позвоночных (включая мозг) закладываются как простые полые структуры, с которыми природа поступает, как стеклодув. Природа может расширить трубочку здесь и сузить ее там, утолщить ее стенки или сделать их тоньше, выдуть боковое ответвление или слепой отросток, согнуть или скрутить трубочку или сделать ее стенки складчатыми – на этом природа удовлетворяется. Форма человеческого желудка может быть легко объяснена с этих позиций – это просто плохо выдутый пузырь; пузырь, рост одной из сторон которого, был замедлен, чтобы не допустить симметричного увеличения в размерах.
V. Fleury, Eur. Phys. J. Appl. Phys. 45, 30101 (2009)
Clarifying tetrapod embryogenesis, a physicist’s point of view [ PDF ]
Several lines of work reviewed here show that the topology of the tetrapods may be directly related to the structure of the earliest movements in embryos. The bio-mechanical approach leads to important consequences for the constraints on evolution of the craniates. Such consequences have received a controversial welcome in the last decade, although they may encapsulate the true origin of craniates, esp. simians, and eventually homo.
Математика в природе: самые красивые закономерности в окружающем мире
От радуг, речных изгибов и теней до паутины, сот и отметин на шкурах животных — видимый мир полон закономерностей, которые можно описать математически. Рассказываем о самых интересных из них.
Читайте «Хайтек» в
Математика в природе
Тюринг, Плато, Геккель, Цейзинг — знаменитые деятели искусства и науки — искали строгие законы математики и находили ее в красоте природы.
Спираль Фибоначчи — геометрическая прогрессия красоты
Спирали распространены среди растений и некоторых животных, особенно среди моллюсков. Например, у моллюсков-наутилид каждая ячейка их раковины — примерная копия следующей, масштабированная константой и выложенная в логарифмическую спираль.
Чаще всего в природе встречается последовательность Фибоначчи. Она начинается с чисел 1 и 1, а затем каждое последующее число получается путем сложения двух предыдущих чисел. Следовательно, после 1 и 1 следующее число — 2 (1 + 1). Следующее число — 3 (1 + 2), затем 5 (2 + 3) и так далее.
С точки зрения физики, спирали — конфигураций низких энергий, которые возникают спонтанно путем самоорганизации процессов в динамических системах. С точки зрения химии, спираль может быть образована реакционно-диффузионным процессом с привлечением как активации, так и ингибирования. Филлотаксис контролируется протеинами, которые управляют концентрацией растительного гормона ауксина, который активирует рост среднего стебля наряду с другими механизмами контроля относительного угла расположения бутона к стеблю. С точки зрения биологии листья расположены настолько далеко друг от друга, насколько позволяет естественный отбор, так как он максимизирует доступ к ресурсам, особенно к солнечному свету, для фотосинтеза.
Фракталы — бесконечное (почти) повторение
Фракталы — еще одна интересная математическая форма, которую каждый видели в природе. Сам Фрактал — это самоподобная повторяющаяся форма, что означает, что одна и та же основная форма появляется снова и снова. Другими словами, если вы увеличите или уменьшите масштаб, везде будет видна одна и та же.
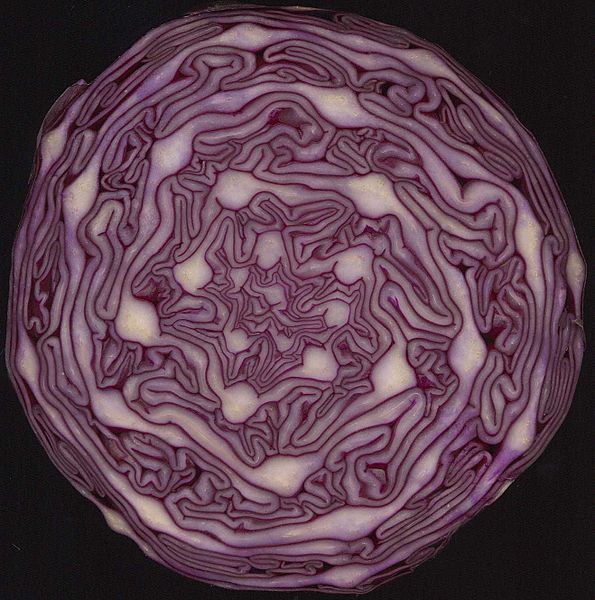
Эти самоподобные циклические математические конструкции, обладающие фрактальной размерностью, встречаются довольно часто, особенно среди растений. Самый известный пример — папоротник.
Кстати, бесконечная повторяемость невозможна в природе, поэтому все фрактальные закономерности — это только аппроксимации (приближения). Например, листья папоротников и некоторых зонтичных растений (например, тмин) являются самоподобными до второго, третьего или четвертого уровня.
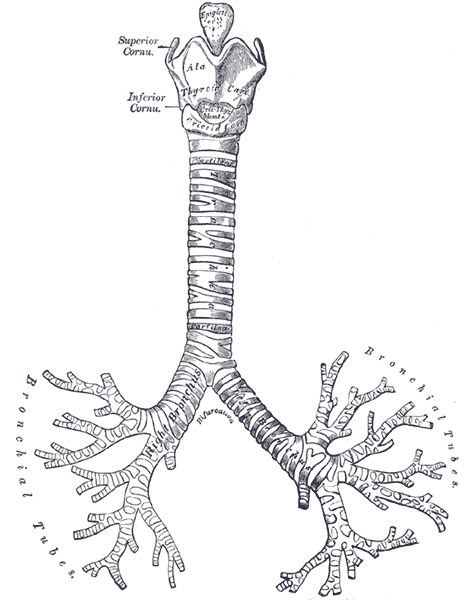
Схожие с папоротником паттерны встречаются также у многих растений (брокколи, капуста сорта Романеско, кроны деревьев и листья растений, плод ананаса), животных (мшанки, кораллы, гидроидные, морские звезды, морские ежи). Также фрактальные паттерны имеют место в структуре разветвления кровеносных сосудов и бронхов животных и человека.
Первые примеры самоподобных множеств с необычными свойствами появились в XIX веке в результате изучения непрерывных недифференцируемых функций (например, функция Больцано, функция Вейерштрасса, множество Кантора). Термин «фрактал» введен Бенуа Мандельбротом в 1975 году и получил широкую известность с выходом в 1977 году его книги «Фрактальная геометрия природы».
Особую популярность фракталы обрели с развитием компьютерных технологий, позволивших эффектно визуализировать эти структуры.
Многоугольники — инженерный гений
При достаточной наблюдательности в живой природе легко обнаружить строгую геометрию. В особом почете оказываются гексагоны — правильные шестиугольники.
Например, соты, в которых пчелы хранят золотистый нектар, — это чудеса инженерного искусства, набор ячеек в форме призмы с правильным шестиугольником в основании. Толщина восковых стенок строго определена, ячейки немного отклоняются от горизонтали, чтобы вязкий мед не вытекал, и соты находятся в равновесии с учетом влияния магнитного поля Земли. А ведь эту конструкцию без чертежей и прогнозов строят множество пчел, которые одновременно работают и как-то координируют свои попытки сделать соты одинаковыми.
Если вы подуете на пузырьки на поверхности воды, чтобы согнать их вместе, то они приобретут форму шестиугольников — или, по крайней мере, приблизятся к ней. Вы никогда не увидите скопище квадратных пузырей: если даже четыре стенки соприкоснутся, они немедленно перестроятся в конструкцию с тремя сторонами, между которыми будут примерно равные углы в 120 градусов. Почему так происходит?
Природа озабочена экономией. Пузыри и мыльная пленка состоят из воды (и слоя мыльных молекул), и поверхностное натяжение сжимает поверхность жидкости таким образом, чтобы она занимала наименьшую площадь. Поэтому капли дождя при падении принимают форму, близкую к сферической: у сферы наименьшая площадь поверхности по сравнению с другими фигурами того же объема. На восковом листке капли воды сжимаются в маленькие бусинки по той же причине.
Поверхностное натяжение объясняет и тот узор, который образуют пузыри или пена. Пена стремится к такой конструкции, при которой общее поверхностное натяжение будет минимальным, а значит, минимальной должна быть и площадь мыльной мембраны. Но конфигурация стенок пузырей должна быть прочной и с точки зрения механики: натяжение в разных направлениях на «перекрестке» должно быть идеально сбалансировано (по тому же принципу нужен баланс при строительстве стен собора). Трехстороннее соединение в пленке из пузырьков и четырехстороннее — в пене — комбинации, которые достигают этого баланса.
Дарси томпсон о росте и форме
Опубликованная в 1859 году книга Чарльза Дарвина «Происхождение видов путем естественного отбора» потрясла западное общество. Однако Дарвин едва ли мог вообразить, что поднятая им буря не уляжется даже через полтора столетия. Хотя серьезные ученые и многие теологи сейчас признают правоту эволюционизма, миллионы людей продолжают его отвергать. Ричард Докинз — всемирно известный биолог, популяризатор науки, атеист, рационалист, «ротвейлер Дарвина» — берется убедить любого непредвзятого читателя в том, что эволюция — это не «просто теория», а всесторонне подкрепленный доказательствами факт.
Художественное оформление и макет Андрея Бондаренко.
Издание осуществлено при поддержке Фонда некоммерческих программ Дмитрия Зимина «ДИНАСТИЯ»
Книга: Самое грандиозное шоу на Земле
Что сделал бы Дарси Томпсон, будь у него компьютер
Что сделал бы Дарси Томпсон, будь у него компьютер
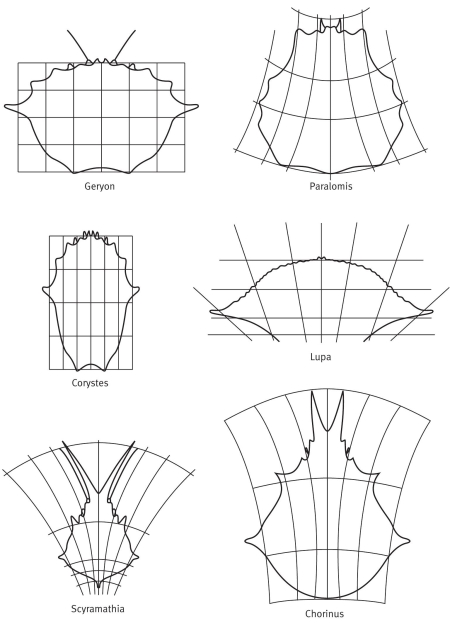
В 1917 году великий шотландский зоолог Дарси Томпсон (D’Arcy Thompson) опубликовал книгу «О росте и форме», в последней главе которой представил миру свой ставший знаменитым метод трансформаций[149]. Суть метода проста: он рисовал животное на миллиметровке, а затем, изменяя масштаб согласно некоторым математическим формулам, демонстрировал превращение животного в родственное этому последнему. Миллиметровку с переменным масштабом можно представить себе листом резины. Нарисуем на ней животное, а потом растянем (или сожмем) ее. Томпсон, например, взял шесть видов крабов и нарисовал на миллиметровке один из них, Geryon. Затем «растянул» миллиметровку пятью способами и получил другие пять видов. Математические подробности нас сейчас не занимают, хотя они очень увлекательны. Но следует понять, что не так-то трудно сделать из одного краба другого. Сам Томпсон не слишком интересовался эволюцией, но нам-то легко представить, как должны были действовать генетические мутации, чтобы добиться таких результатов. Конечно, мы не будем считать Geryon или какой-то из пяти других видов предком остальных. Никто из них не был таковым, и дело не в этом. Суть достижения Томпсона — в демонстрации того, что как бы ни выглядел общий предок этих крабов, трансформация такого рода может превратить любого из них (как и общего предка) в любой другой.
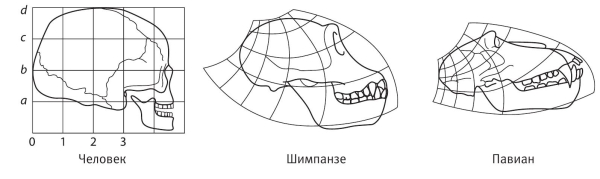
Эволюция никогда не происходила посредством превращения одной взрослой особи в другую. Вспомним, что любая взрослая особь начинает существование с эмбриона. Мутация проявляется в развитии эмбриона — как изменение скорости роста частей относительно друг друга. В главе 7 мы именно так интерпретировали эволюцию черепа человека. Следовательно, если мы нарисуем человеческий череп на «резиновой миллиметровке», то преобразованиями а-ля Томпсон сможем превратить его в череп близкого родственника, например шимпанзе, или (с большими искажениями) в череп павиана. Именно это продемонстрировал Томпсон. Заметьте, что начинать с человеческого черепа необязательно: он мог взять череп шимпанзе и получить череп человека. А еще лучше для книги по эволюции (каковой книга Томпсона не являлась) расположить на «резиновой миллиметровке» череп австралопитека и растянуть ее до черепа современного человека. Получилось бы ничуть не хуже, чем на приведенных рисунках, а с эволюционной точки зрения было бы куда осмысленней.
Зоологи знали о гомологии еще до Дарвина и говорили, что, например, крыло мыши гомологично руке человека. Знай они математику лучше, они бы говорили: «гомеоморфно». После Дарвина, когда наличие у летучей мыши и человека общего предка перестало подвергаться сомнению, зоологи стали определять гомологичность в эволюционных терминах, считая гомологичными органы, унаследованные от общего предка. Термин «аналогичный» стали применять в отношении органов со сходными функциями, но без общего происхождения. Например, крыло мыши аналогично крылу насекомого и гомологично человеческой руке. Итак, если мы хотим применять гомологии как аргумент в пользу эволюционной теории, мы должны отказаться от эволюционного определения гомологии, чтобы не угодить в замкнутый круг. Поэтому нам будет пока удобнее пользоваться доэволюционным определением. Крыло мыши и рука человека гомеоморфны, поскольку одно можно получить из другого преобразованием Томпсона. Превратить таким способом крыло мыши в крыло насекомого не получится из-за отсутствия в последнем соответствующих деталей. Широко распространенные гомеоморфизмы, которые определены без помощи эволюции, пригодны для доказательства эволюции. Нетрудно показать, как эволюция могла превратить руку одного позвоночного в руку любого другого, изменяя скорость роста частей руки у эмбриона.
С того момента, когда в 1960-х, будучи студентом-старшекурсником, я познакомился с компьютерами, я задавался вопросом, что сделал бы Томпсон, если бы у него был компьютер. Вопрос стал актуален в 1980-х, с появлением доступных компьютеров с графическим дисплеем. Рисование на растяжимой подложке просто просилось на экран компьютера. Я предложил Оксфордскому университету подать заявку на грант, чтобы нанять программиста для реализации алгоритма Томпсона с удобным общедоступным интерфейсом. Мы получили деньги, и я нанял Уилла Аткинса, первоклассного программиста и биолога, который стал моим другом и советчиком. Когда он справился с широким репертуаром дисторсий Томпсона, ему уже не составляло труда научить этому программу искусственного отбора биоморфов, о которой я рассказывал в главе 2. «Игроку» предлагаются организмы, из которых он может выбрать один для «разведения». Как и прежде, процессом управляют гены, переходящие из поколения в поколение, однако теперь они управляют формой организма (растягивая или сжимая «резиновую миллиметровку», на которой он нарисован). Теоретически можно, начав с черепа австралопитека, добиться постепенного увеличения лобных долей и уменьшения длины морды по мере приближения к современному человеку. На деле же это оказалось довольно трудной задачей.
Одна из причин, на мой взгляд, по-прежнему заключается в том, что преобразование Томпсона преображает одну взрослую форму в другую. В главе 8 я упоминал, что генетически обусловленная эволюция работает иначе. У каждого животного есть история развития. Путь от эмбриона до взрослого организма лежит через непропорциональную скорость роста отдельных частей тела. Эволюция — это не управляемое генами преобразование одного взрослого организма в другой, а управляемое генами изменение программы развития. Сэр Джулиан Хаксли (правнук Томаса и брат Олдоса[151]) осознал это, когда, вскоре после выхода первого издания книги Томпсона, попытался приспособить его метод для изучения превращения эмбриона на разных стадиях развития. Здесь мы на время, до последней главы книги, оставим метод Томпсона.
Сравнительная анатомия, как я отмечал, свидетельствует в пользу эволюционной теории даже убедительнее ископаемых остатков. Этой точки зрения придерживался и Дарвин, высказавший ее в конце главы «Взаимное родство организмов» «Происхождения видов»:
Наконец, различные группы фактов, рассмотренные в этой главе, по-моему, столь ясно указывают, что бесчисленные виды, роды и семейства, населяющие земной шар, произошли каждый в пределах своего класса или группы от общих предков и затем модифицированы в процессе наследования, что я без колебаний принял бы этот взгляд, если бы даже он не был подкреплен другими фактами или аргументами[152].











 nature_wonder
nature_wonder