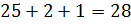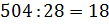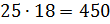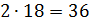деление числа в данном отношении правило

Деление числа в данном отношении + задачи с решением

В шестом классе изучается тема деления чисел в данном отношении. Тема для учеников не всегда понятна с первого объяснения учителя, поэтому разберем ее подробнее на страницах сайта 7 гуру. Напишем понятия и правила, разберем примеры решения задач на деление в данном отношении.

Понятие отношения

Частное двух не равных нулю чисел a и b называется отношением чисел a и b. Числа a и b называются членами отношения.

Скорость – это отношение пройденного пути ко времени, за которое этот путь пройден.
Скорость сближения – это расстояние, на которое сближаются объекты за единицу времени.
Цена товара – это отношение стоимости товара к его массе или количеству единиц товара.

Правило деления числа в данном отношении.

Чтобы разделить число c в отношении a к b, можно разделить число c на сумму членов отношения a + b и результат умножить на каждый член отношения, числа a, b и c не равны нулю.

Задача 1. Разделите между двумя друзьями 80 конфет в отношении 1:4.

1 способ:
Таким способом мы решали подобные задачи в начальной школе. Сначала узнаем, сколько всего частей в целом. Узнаем количество предметов в одной части. Умножаем на нужные количества частей, чтобы ответить на вопрос.

2 способ:
Решаем по правилу деления числа на части. Этим способом предпочтительнее пользоваться при решении подобных задач.

Ответ: конфеты между друзьями надо разделить так: первому – 16 конфет, а второму – 64 конфеты.

Задача 2. Сестра и брат сложили свои деньги для покупки лотерейного билета. У сестры было 50 рублей, а у брата 30 рублей. Билет выиграл 4000 рублей. Как они должны разделить эти деньги между собой?

Ответ: 2500 рублей, 1500 рублей.

Задача 3. Трое хотят купить фирму по продаже мороженого. Первый желает иметь 6 частей акций, второй – 4 части акций, третий – 2 части. Всего нужно заплатить 960 000 рублей. Сколько денег должен внести каждый из них.

Ответ: 480 000 рублей, 320 000 рублей, 160 000 рублей.

Задача 4. Первая машинистка печатает 180 страниц за 20 часов, а вторая – за 30 часов. Как распределить между ними 180 страниц, чтобы они напечатали их в кратчайший срок?

Ответ: первой машинистке – 108 страниц, второй – 72 страницы.

Задача 5. Мотоциклист может проехать расстояние между пунктами за 4 часа, а велосипедист – за 12 часов. Однажды они одновременно отправились навстречу друг другу из этих пунктов. Сколько километров проедет каждый до встречи, если расстояние между пунктами 120 километров?

Так как время преодоления расстояния мотоциклистом и велосипедистом равно 12:4, значит, скорость мотоциклиста будет в 3 раза больше, чем велосипедиста. Следовательно, за одно и то же время мотоциклист проедет в 3 раза большее расстояние. Это значит, что весь путь делится между ними в отношении 1:3.

Задача 6. Сортировка элементов по категориям. Поставьте в соответствующие столбцы (1:4; 2:5) числа, которые можно разделить нацело в заданных отношениях. Варианты ответов: 25, 13, 14, 45, 28, 6.

Для решения нужно сначала посчитать сумму частей первого столбца:
1 + 4 = 5
Затем проверить, какие из чисел кратны 5. Это 25 и 45.
Аналогично для второго столбца.
2 + 5 = 7
Числа, кратные 7: 14 и 28.

Источник

Математика. 6 класс

Конспект урока

Деление числа в данном отношении

Перечень вопросов, рассматриваемых в теме:

Частное двух не равных нулю чисел a и b называется отношением чисел a и b.

Числа a и b называются членами отношения.

Скорость – это отношение пройденного пути ко времени, за которое этот путь пройден.

Скорость сближения – это расстояние, на которое сближаются объекты за единицу времени.

Цена товара – это отношение стоимости товара к его массе или количеству единиц товара.

Теоретический материал для самостоятельного изучения

Сегодня мы с вами разберём, что означает деление числа в данном отношении.

Правило деления числа в данном отношении.

Чтобы разделить число c в отношении a к b, можно разделить число c на сумму членов отношения a + b и результат умножить на каждый член отношения, числа a, b и c не равны нулю.

Ответ: конфеты между друзьями надо разделить так: первому – 16 конфет, а второму – 64 конфеты.

Сестра и брат сложили свои деньги для покупки лотерейного билета. У сестры было 50 рублей, а у брата 30 рублей. Билет выиграл 4000 рублей. Как они должны разделить эти деньги между собой?

Ответ: 2500 рублей, 1500 рублей.

Трое хотят купить фирму по продаже мороженого. Первый желает иметь 6 частей акций, второй – 4 части акций, третий – 2 части. Всего нужно заплатить 960 000 рублей. Сколько денег должен внести каждый из них.

Ответ: 480 000 рублей, 320 000 рублей, 160 000 рублей.

Первая машинистка печатает 180 страниц за 20 часов, а вторая – за 30 часов. Как распределить между ними 180 страниц, чтобы они напечатали их в кратчайший срок?

Ответ: первой машинистке – 108 страниц, второй – 72 страницы.

Мотоциклист может проехать расстояние между пунктами за 4 часа, а велосипедист – за 12 часов. Однажды они одновременно отправились навстречу друг другу из этих пунктов. Сколько километров проедет каждый до встречи, если расстояние между пунктами 120 километров?

Разбор решения заданий тренировочного модуля

№1. Тип задания: сортировка элементов по категориям.

Поставьте в соответствующие столбцы числа, которые можно разделить нацело в заданных отношениях.

№2. Тип задания: подчеркивания.

Нужно подчеркнуть правильный вариант ответа.

Источник

Математика. 6 класс

Конспект урока

Деление числа в данном отношении

Перечень вопросов, рассматриваемых в теме:

Частное двух не равных нулю чисел a и b называется отношением чисел a и b.

Числа a и b называются членами отношения.

Скорость – это отношение пройденного пути ко времени, за которое этот путь пройден.

Скорость сближения – это расстояние, на которое сближаются объекты за единицу времени.

Цена товара – это отношение стоимости товара к его массе или количеству единиц товара.

Теоретический материал для самостоятельного изучения

Сегодня мы с вами разберём, что означает деление числа в данном отношении.

Правило деления числа в данном отношении.

Чтобы разделить число c в отношении a к b, можно разделить число c на сумму членов отношения a + b и результат умножить на каждый член отношения, числа a, b и c не равны нулю.

Ответ: конфеты между друзьями надо разделить так: первому – 16 конфет, а второму – 64 конфеты.

Сестра и брат сложили свои деньги для покупки лотерейного билета. У сестры было 50 рублей, а у брата 30 рублей. Билет выиграл 4000 рублей. Как они должны разделить эти деньги между собой?

Ответ: 2500 рублей, 1500 рублей.

Трое хотят купить фирму по продаже мороженого. Первый желает иметь 6 частей акций, второй – 4 части акций, третий – 2 части. Всего нужно заплатить 960 000 рублей. Сколько денег должен внести каждый из них.

Ответ: 480 000 рублей, 320 000 рублей, 160 000 рублей.

Первая машинистка печатает 180 страниц за 20 часов, а вторая – за 30 часов. Как распределить между ними 180 страниц, чтобы они напечатали их в кратчайший срок?

Ответ: первой машинистке – 108 страниц, второй – 72 страницы.

Мотоциклист может проехать расстояние между пунктами за 4 часа, а велосипедист – за 12 часов. Однажды они одновременно отправились навстречу друг другу из этих пунктов. Сколько километров проедет каждый до встречи, если расстояние между пунктами 120 километров?

Разбор решения заданий тренировочного модуля

№1. Тип задания: сортировка элементов по категориям.

Поставьте в соответствующие столбцы числа, которые можно разделить нацело в заданных отношениях.

№2. Тип задания: подчеркивания.

Нужно подчеркнуть правильный вариант ответа.

Источник

Урок математики на тему «Деление числа в данном отношении»

Ищем педагогов в команду «Инфоурок»

Тема: Деление числа в данном отношении. Тип урока: урок отработки умений и рефлексии

Цель: Развитие навыка самостоятельности в работе, трудолюбия, аккуратности, развитие навыков самоанализа и самоконтроля при оценке результата и процесса своей деятельности; формирование информационной, коммуникативной и учебной компетентности учащихся, умения работать с имеющейся информацией в новой ситуации; повторить правила деления числа в данном отношении. Научиться применять правило при решении заданий.

Коррекционная цель: корректировать устную и письменную математическую речь, умение применять теоретические знания в практике; коррекция и развитие памяти; коррекция и развитие мыслительной деятельности.

1. Предметные: совершенствовать деления числа в данном отношении.

2. Метапредметные: формирование умения самостоятельно формулировать учебную задачу урока, развитие операций мышления (сравнение, сопоставление, выделение лишнего, обобщение, классификация), формирование отдельных составляющих исследовательской деятельности (умения наблюдать, умения делать выводы и умозаключения, умения выдвигать и формулировать гипотезы).

3. Личностные: обеспечить познавательную мотивацию учащихся при изучении новых понятий и определений, провести рефлексию деятельности после проделанной работы.

Ресурсы урока: учебник С.М. Никольского, раздаточный материал (задания на карточках).

Межпредметные связи: математика-русский язык, математика-география, математика-физика, математика-литература.

Приветствие, проверка отсутствующих и готовность учащихся

Приветствие учителя, готовность к уроку

Проверка домашнего задания

Учитель проверяет домашнее задание, выясняет, с какими трудностями столкнулись учащиеся при его выполнении.

Вместе с учителем проверяют правильность выполнения домашнего задания. Задают вопросы.

Актуализация опорных знаний

— Основное свойство отношения.

-Определение деление числа в данном отношении.

1. Разделите число 5 в отношении 2:5.

2. Обьясните как разделить 24 в отношении 1:2:3.

Отвечают на вопросы учителя с комментированием.

(взаимодействуют с учителем во время ответа).

Формулируют тему и цель урока.

— Итак, повторили. Теперь нам с вами необходимо выполнить исследование.

Самостоятельная работа по теме «Деление числа в данном отношении». (20 мин)

1. Разделите число 114 на две части в отношении 7 : 12.

2. Разделите число 525 на три части в отношении 5 : 7 : 9.

3. Сахарный сироп состоит из 11 частей воды и 3 частей сахара. Сколько сахара надо взять, чтобы получить 280 г сиропа?

1. Разделите число 64 на две части в отношении 3 : 5.

2. Разделите число 480 на три части в отношении 3 : 4 : 5.

3. Раствор содержит 5 частей кислоты и 8 частей воды. Сколько кислоты надо, чтобы получить 442 г раствора??

Дополнительное задание №44.

-Самостоятельно выполняют задание, осуществляют взаимопроверку, оценивают.

1. Разделите число 114 на две части в отношении 7 : 12.

1) ;

2) . Ответ: 42; 72.

2. Разделите число 525 на три части в отношении 5 : 7 : 9.

1) ;

2) ;

3) . Ответ: 125; 175; 225.

(г) – сахара надо взять. Ответ: 60 г.

1. Разделите число 64 на две части в отношении 3 : 5.

1) ;

2) . Ответ: 24; 40.

2. Разделите число 480 на три части в отношении 3 : 4 : 5.

1) ;

2) ;

3) . Ответ: 120; 160; 200.

(г) – кислоты надо взять. Ответ: 170 г.

Учитель организует обсуждение того, что было сделано на уроке. Выставление оценок.

1. Оценивают степень достижения цели, определяют круг новых вопросов.

2. Выборочно высказываются, делятся друг с другом мнением.

Предложить учащимся закончить предложения:

сегодня я узнал… было интересно…
было трудно… я выполнял задания…
я понял, что… теперь я могу…
я приобрел… я научился…
у меня получилось …

Источник

Деление числа в данном отношении

Урок 23. Математика 6 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Деление числа в данном отношении»

Представим себе такую историю…

– Саша, чем ты занимаешься? – поинтересовался у друга Паша.

– Хочу приготовить мороженое, – ответил Саша. – Уже и рецепт нашёл, и подготовил все ингредиенты, но вот только разобраться не могу, сколько чего брать.

– А что в рецепте написано? – уточнил Паша.

– В рецепте сказано, что для приготовления мороженого нужно смешать 3 части молока, 2 части сливок и 1 часть сахара, – прочитал Саша. – А как эти части высчитать, если я хочу приготовить, например, 3 килограмма мороженого?

– И вправду, сложная задача у тебя получается, – задумался Паша. – Как эти части считать, не понятно. Но я знаю, кто нам сможет помочь!

– Ребята, прежде чем я отвечу на ваш вопрос, давайте немного разомнёмся и выполним устные задания, – предложил Мудряш.

– Давайте сверимся! – сказал Мудряш. — Посмотрите, что у вас должно было получиться!

– Ну а теперь вернёмся к вашему вопросу, – начал Мудряш. – Чтобы ответить на вопрос «Сколько каких ингредиентов нужно взять для приготовления смеси мороженого?», прежде всего нужно научиться выполнять деление числа в данном отношении. Итак, вы хотите приготовить 3 килограмма мороженого. Для удобства давайте переведём килограммы в граммы, всё же так будет легче и привычнее считать.

– Так как 1 килограмм равен 1000 грамм, – стал размышлять Саша, – значит, я хочу приготовить 3000 грамм мороженого.

– Хорошо! – согласился Мудряш. – По рецепту для приготовления мороженого нужно смешать 3 части молока, 2 части сливок и 1 часть сахара. Будем считать, что смесь мороженого состоит из 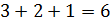частей, имеющих одинаковые массы. Тогда как посчитать, сколько приходится на 1 часть?

– Нужно 3000 разделить на 6, – ответил Паша.

– Правильно! – сказал Мудряш. – Значит, масса одной части смеси равна 500 граммам. По рецепту молоко в смеси составляет 3 части, сливки – 2 части, а сахар – 1 часть. Посчитайте, чему же будут равны эти части.

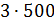
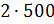
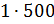
– Тогда масса молока в смеси будет равна и равна 1500 граммам, – принялся считать Саша. – Масса сливок будет равна и равна 1000 грамм, а масса сахара будет равна и равна 500 граммам.

– Получается, что для приготовления 3 килограммов мороженого нужно взять 1500 грамм молока, добавить 1000 грамм сливок, а затем добавить 500 грамм сахара? – решил уточнить Паша.

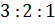
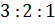
– Всё верно! – согласился Мудряш. – Из решения вашей задачи следует, что число 3000 можно представить в виде суммы трёх слагаемых – 1500, 1000 и 500, отношение которых равно . В таких случаях говорят, что число 3000 разделили в отношении . Также можно сказать, что число 3000 представили в виде суммы трёх слагаемых, пропорциональных числам 3, 2 и 1.

– И совсем несложная задача оказалась, – заметил Саша. – Теперь я без труда могу приготовить мороженое.

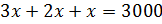
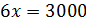
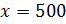
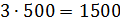
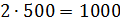
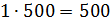
– Эту же задачу можно было решить и другим способом, – продолжил Мудряш. – Пусть масса одной части смеси мороженого составляет х грамм. Тогда массы молока, сливок и сахара составляют соответственно 3х грамм, 2х грамм и х грамм. Поскольку масса всей смеси мороженого равна 3000 грамм, то можем составить уравнение . Решим это уравнение. Получим, что . Отсюда . Тогда массы молока, сливок и сахара равны соответственно грамм, грамм и грамм.

– Сделаем вывод, – сказал Мудряш. – Чтобы разделить число в данном отношении, можно разделить это число на сумму членов отношения, а затем результат умножить на каждый член отношения.

– А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним несколько заданий.

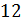
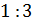
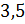
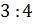
Задание первое: разделите числа в указанных отношениях: а) число в отношении ; б) число в отношении .

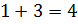
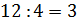
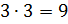
Решение: нужно разделить число 12 в отношении 1 к 3. Будем считать, что всё число состоит из частей. Значит, 1 часть равна . Тогда 3 части будут равны . Следовательно, число двенадцать можно разделить в отношении 1 к 3 так: 3 и 9.

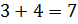
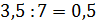
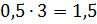
В следующем условии нам нужно разделить число 3,5 в отношении 3 к 4. Будем считать, что всё число состоит из частей. Тогда 1 часть равна . Отсюда 3 части числа равны . Следовательно, число 3,5 можно разделить в отношении 3 к 4 так: 1,5 и 2.

Следующее задание: два числа относятся как 4 к 7. Найдите эти числа, зная, что: их сумма равна 110, их разность равна 12.

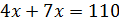
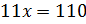
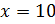
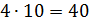
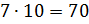
Решение: обозначим за х одну часть. Тогда можем записать, что первое число равно 4х, второе – 7х. В первом условии сказано, что сумма этих чисел равна 110. Составим уравнение . Решим его. Получим . Отсюда . Значит, первое число равно , второе – .

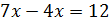
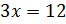
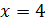
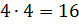
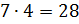
Во втором условии сказано, что разность этих чисел равна 12. Составим уравнение . Решим его. Получим . Отсюда . Значит, первое число равно , второе – .

Решим задачу: стороны прямоугольника 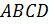относятся как 2 к 3. Найдите площадь этого прямоугольника, если его периметр равен 20 сантиметров.

И решим ещё одну задачу. Для приготовления фарфора смешивают 25 частей белой глины, 2 части песка и 1 часть гипса. Сколько нужно взять каждого материала, чтобы приготовить 504 грамма смеси?

Решение: будем считать, что вся смесь состоит из частей, имеющих одинаковые массы. Тогда 1 часть содержит грамм. Следовательно, чтобы приготовить 504 грамма смеси фарфора, нужно взять: грамм белой глины, грамм песка и грамм гипса.

Источник