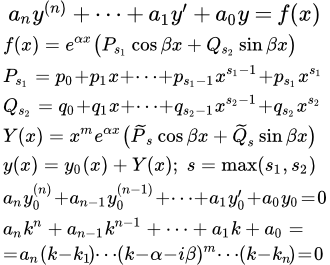диф уравнения со специальной правой частью

Диф уравнения со специальной правой частью

Пусть общее решение однородного дифференциального уравнения второго порядка имеет вид: \[\left( x \right) = \left( x \right) + \left( x \right).\] Вместо постоянных \(\) и \(\) будем рассматривать вспомогательные функции \(\left( x \right)\) и \(\left( x \right).\) Будем искать эти функции такими, чтобы решение \[y = \left( x \right)\left( x \right) + \left( x \right)\left( x \right)\] удовлетворяло неоднородному уравнению с правой частью \(f\left( x \right).\)

Неизвестные функции \(\left( x \right)\) и \(\left( x \right)\) определяются из системы двух уравнений: \[\left\< \begin \left( x \right)\left( x \right) + \left( x \right)\left( x \right) = 0\\ \left( x \right) \left( x \right) + \left( x \right) \left( x \right) = f\left( x \right) \end \right..\]

Подчеркнем, что данный метод работает лишь для ограниченного класса функций в правой части, таких как

\(f\left( x \right) = \left[ <\left( x \right)\cos\left( <\beta x>\right) + \left( x \right)\sin\left( <\beta x>\right)> \right]>,\) где \(<\left( x \right)>\) и \(<\left( x \right)>\) − многочлены степени \(n\) и \(m,\) соответственно.

В обоих случаях выбор частного решения должен соответствовать структуре правой части неоднородного дифференциального уравнения.

В случае \(1,\) если число \(\alpha\) в экспоненциальной функции совпадает с корнем характеристического уравнения, то частное решение будет содержать дополнительный множитель \(,\) где \(s\) − кратность корня \(\alpha\) в характеристическом уравнении.

В случае \(2,\) если число \(\alpha + \beta i\) совпадает с корнем характеристического уравнения, то выражение для частного решения будет содержать дополнительный множитель \(x.\)

Неизвестные коэффициенты можно определить подстановкой найденного выражения для частного решения в исходное неоднородное дифференциальное уравнение.

Если правая часть неоднородного уравнения представляет собой сумму нескольких функций вида \[ <\left( x \right)>\;\;\text<и/или>>\;\; <\left[ <\left( x \right)\cos\left( <\beta x>\right) + \left( x \right)\sin\left( <\beta x>\right)> \right]>,> \] то частное решение дифференциального уравнения также будет являться суммой частных решений, построенных отдельно для каждого слагаемого в правой части.

Источник

Лекция 8. Линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами

Зміст

4.1 Основные определения

Линейное дифференциальное уравнение (ЛДУ) 2-го порядка с постоянными коэффициентами имеет вид

Если f ( x ) =0, уравнение (4.1) называется однородным, в противном случае – неоднородным. Например, уравнения

– линейные однородные дифференциальные уравнения (сокращенно ЛОДУ), т.к. их правые части равны нулю. Уравнения (4.2) и

– ЛНДУ (линейные неоднородные дифференциальные уравнения).

4.2 Решение ЛОДУ второго порядка с постоянными коэффициентами

По определению, ЛОДУ 2-го порядка имеет вид

План нахождения общего решения этого уравнения:

1) Написать характеристическое уравнение для (4.3)

3) В зависимости от значений p ₁ и p ₂ найти общее решение y :

ЛНДУ 2-го порядка с постоянными коэффициентами и правой частью специального вида

5.1 Теорема об общем решении ЛНДУ

По определению линейное неоднородное дифференциальное уравнение (ЛНДУ) 2-го порядка имеет вид

Сопоставим ему однородное уравнение

Теорема. Общее решение уравнения (5.1) есть сумма общего решения уравнения (5.2) и частного решения уравнения (5.1):

где y _O.O. – общее решение соответствующего однородного уравне­ния (5.2), а y _Ч.Н. – частное решение уравнения (5.1).

Здесь о.о. означает «общее однородное», а ч.н. – «частное неоднородное».

Способ нахождения решения y _O.O. указан в п. 4.2. Способ нахождения y _Ч.Н. зависит от правой части f ( x ) уравнения (5.1). Мы рассмотрим три случая:

5.2 Уравнения с правой частью вида f(x) = Ae^γx

В этом случае уравнение (5.1) имеет вид

где A и γ – числа. Тогда его частное решение

5.3 Уравнения с правой частью вида P(x)e^αx

Пример. Решить уравнение y’ ‘ + 3 y’ = 9 x

2) Так как α = 0 совпадает с одним корнем характеристического уравнения, то k = 1.

5.4 Уравнения с правой частью вида (Pcosβx+Qsinβx)e^αx

Рассмотрим решение ЛНДУ с правой частью вида

Общее решение ЛНДУ находят по формуле (5.3). Нахождение ее слагаемого y O.O. рассмотрено в разделе 4.2, а слагаемое y _Ч.Н. для правой части вида (5.7) имеет вид

Правая часть уравнения имеет вид (5.10) с P = 2, Q = 6, α = 0, β = 1.

2) Так как α + i β = i не равно ни одному корню характеристического уравнения, то k = 0.

3) По формуле (5.8) частное решение

4) Найдем числа A и B (неопределенные коэффициенты). Для этого найдем производные y’ _Ч.Н. и y» _Ч.Н. :

и подставим их и y _Ч.Н. в левую часть данного уравнения. Получим

Складывая и вычитая уравнения, находим

5) Подставляем эти значения в формулу п.3):

6) Общее решение данного уравнения по формуле (5.3) есть

Принцип суперпозиции. Решение системы ЛОДУ 2-го порядка с постоянными коэффициентами

6.1 Принцип суперпозиции

Теорема. Общее решение уравнения

6.3 Решение системы ЛОДУ 2-го порядка с постоянными коэффициентами методом исключения неизвестных

Суть этого метода решения системы (6.2) такова: из одного уравнения системы выразить x через y (или y через x ), подставить в другое уравнение и решить полученное ЛОДУ с одним неизвестным. Более подробно план решения таков.

3) Подставить найденные выражения для y и в другое уравнение системы.

4) Решить полученное ЛОДУ (найти x ).

6) Записать общее решение системы.

Источник

Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Данная статья раскрывает вопрос о решении линейных неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами. Будет рассмотрена теория вместе с примерами приведенных задач. Для расшифровки непонятных терминов необходимо обращаться к теме об основных определениях и понятиях теории дифференциальных уравнений.

Перейдем к формулировке теоремы общего решения ЛНДУ.

Теорема общего решения ЛДНУ

, где исходным неоднородным уравнением является y = y 0 + y

Отсюда видно, что решение такого уравнения второго порядка имеет вид y = y 0 + y

. Алгоритм нахождения y 0 рассмотрен в статье о линейных однородных дифференциальных уравнениях второго порядка с постоянными коэффициентами. После чего следует переходить к определению y

является частным решением y

Решение

Общим решением линейного неоднородного уравнения является сумма общего решения, которое соответствует уравнению y 0 или частному решению неоднородного уравнения y

Для начала найдем общее решение для ЛНДУ, а после чего – частное.

Получили, что корни различные и действительные. Поэтому запишем

. Видно, что правая часть заданного уравнения является многочленом второй степени, тогда один из корней равняется нулю. Отсюда получим, что частным решением для y

Найдем их из равенства вида y

Эта запись называется общим решением исходного линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами.

Применив теорему Коши, имеем, что

Коэффициенты, принадлежащие Q n ( x ) находятся по равенству y

Решение

Уравнение общего вида y = y 0 + y

‘ = e x · A x 2 + B x + C ‘ = e x · A x 2 + B x + C + e x · 2 A x + B = = e x · A x 2 + x 2 A + B + B + C y

‘ ‘ = e x · A x 2 + x 2 A + B + B + C ‘ = = e x · A x 2 + x 2 A + B + B + C + e x · 2 A x + 2 A + B = = e x · A x 2 + x 4 A + B + 2 A + 2 B + C

Ответ: видно, что y

Решение

Имеем пару комплексно сопряженных корней. Преобразуем и получим:

y 0 = e 0 · ( C 1 cos ( 2 x ) + C 2 sin ( 2 x ) ) = C 1 cos 2 x + C 2 sin ( 2 x )

будет производиться из y

Необходимо приравнять коэффициенты синусов и косинусов. Получаем систему вида:

Ответ: общим решением исходного ЛНДУ второго порядка с постоянными коэффициентами считается

Решение

По условию видно, что

= e α x · ( L m ( x ) sin ( β x ) + N m ( x ) cos ( β x ) · x γ = = e 3 x · ( ( A x + B ) cos ( 5 x ) + ( C x + D ) sin ( 5 x ) ) · x 0 = = e 3 x · ( ( A x + B ) cos ( 5 x ) + ( C x + D ) sin ( 5 x ) )

Нахождение производной и подобных слагаемых дает

После приравнивания коэффициентов получаем систему вида

Из всего следует, что

= e 3 x · ( ( A x + B ) cos ( 5 x ) + ( C x + D ) sin ( 5 x ) ) = = e 3 x · ( ( x + 1 ) cos ( 5 x ) + ( x + 1 ) sin ( 5 x ) )

Ответ: теперь получено общее решение заданного линейного уравнения:

= = C 1 e x + C 2 e 2 x + e 3 x · ( ( x + 1 ) cos ( 5 x ) + ( x + 1 ) sin ( 5 x ) )

Алгоритм решения ЛДНУ

Любой другой вид функции f ( x ) для решения предусматривает соблюдение алгоритма решения:

Решение

Необходимо произвести решение относительно C 1 ‘ ( x ) и C 2 ‘ ( x ) при помощи любого способа. Тогда запишем:

Отсюда следует, что общее решение будет иметь вид:

Ответ: y = y 0 + y

Источник

Диф уравнения со специальной правой частью

Случай для линейного неоднородного дифференциального уравнения с постоянными коэффициентами и с правой частью имеющей вид полинома от x степени m

Для уравнения с постоянными коэффициентами в случае, когда правая часть имеет специальный вид, удается найти частное решение методом неопределенных коэффициентов (методом подбора частных решений).

Рассмотрим этот метод для уравнения n-го порядка вида

где a₁, …, a_n — действительные числа, α — действительное число, P_m (x) — полином от x степени m, которая может быть равной нулю, так что этот полином может вырождаться в число, отличное от нуля.

Метод неопределенных коэффициентов состоит в том, что задается вид частного решения с неопределенными коэффициентами, которые определяются подстановкой в данное уравнение. Вид частного решения уравнения зависит от того, совпадает ли число α с корнями характеристического уравнения:

где Q_m (x) — полином степени m с коэффициентами, подлежащими определению.

Случай для линейного неоднородного дифференциального уравнения с постоянными коэффициентами и с правой частью имеющей вид:

где α и b — действительные числа, P₁ и P₂ — полиномы от x, старшая степень которых равна m, так что один из них обязательно имеет степень m, а степень другого не превосходит m, и он может быть даже тождественно равен нулю.

Укажем вид частного решения уравнения (14.2) в двух случаях:

где Q₁ и Q₂ — полиномы степени m с неопределенными коэффициентами; причем надо брать оба эти полинома даже в том случае, когда один из полиномов P₁ и P₂ тождественно равен нулю.

f (x) = 8e3x ⇒ α = 3, β = 0, s = 0.
При этом число α ±βi = 3 не является корнем характеристического урав-
нения. Поэтому частное решение y

неоднородного уравнения надо искать
в виде

Источник

Решение линейных дифференциальных уравнений с постоянными коэффициентами со специальной неоднородной частью

Определение общего решения по известному частному решению

Если неоднородная часть может быть представлена в виде суммы функций:
,
то частное решение также может быть представлено в виде суммы частных решений:
,
каждое из которых удовлетворяет уравнению с правой частью в виде одной из функций :
.

Как правило, легче найти частные решения от более простых неоднородных частей, а затем получить частное решение для всего уравнения суммированием полученных частных решений.

Метод решения линейных ДУ с постоянными коэффициентами со специальной неоднородной частью

Это уравнение можно решить общим методом понижения порядка. Однако существует более простой способ, основанный на том, что частное решение такого уравнения имеет определенный вид. Суть этого метода заключается в следующем.

Далее устанавливаем вид частного решения исходного уравнения (2). Оно выражается через многочлены, экспоненту, синусы и косинусы, которые входят в частное решение с неизвестными коэффициентами. Установив вид частного решения, подставляем в уравнение (2). Приравнивая левую и правую части, находим неизвестные коэффициенты.

После этого общее решение исходного уравнения (2) равно сумме общего решения однородного уравнения плюс частное решение неоднородного:
.

Установление вида частного решения

Частные случаи

Неоднородность в виде многочлена

Если характеристическое уравнение (4) имеет нулевой корень кратности p :
,
то частное решение имеет вид:
.

Неоднородность в виде произведения экспоненты и многочлена

Если среди корней характеристического уравнения нет действительного корня со значением α :
,
то частное решение является произведением многочлена степени s и экспоненты:
.

Если характеристическое уравнение (4) имеет действительный корень α кратности p :
,
то частное решение имеет вид:
.

Неоднородность в виде суммы произведений многочленов на косинус и синус

Источник