дифференциальные уравнения второго порядка с правой частью специального вида

Дифференциальные уравнения второго порядка с правой частью специального вида

Пусть общее решение однородного дифференциального уравнения второго порядка имеет вид: \[\left( x \right) = \left( x \right) + \left( x \right).\] Вместо постоянных \(\) и \(\) будем рассматривать вспомогательные функции \(\left( x \right)\) и \(\left( x \right).\) Будем искать эти функции такими, чтобы решение \[y = \left( x \right)\left( x \right) + \left( x \right)\left( x \right)\] удовлетворяло неоднородному уравнению с правой частью \(f\left( x \right).\)

Неизвестные функции \(\left( x \right)\) и \(\left( x \right)\) определяются из системы двух уравнений: \[\left\< \begin \left( x \right)\left( x \right) + \left( x \right)\left( x \right) = 0\\ \left( x \right) \left( x \right) + \left( x \right) \left( x \right) = f\left( x \right) \end \right..\]

Подчеркнем, что данный метод работает лишь для ограниченного класса функций в правой части, таких как

\(f\left( x \right) = \left[ <\left( x \right)\cos\left( <\beta x>\right) + \left( x \right)\sin\left( <\beta x>\right)> \right]>,\) где \(<\left( x \right)>\) и \(<\left( x \right)>\) − многочлены степени \(n\) и \(m,\) соответственно.

В обоих случаях выбор частного решения должен соответствовать структуре правой части неоднородного дифференциального уравнения.

В случае \(1,\) если число \(\alpha\) в экспоненциальной функции совпадает с корнем характеристического уравнения, то частное решение будет содержать дополнительный множитель \(,\) где \(s\) − кратность корня \(\alpha\) в характеристическом уравнении.

В случае \(2,\) если число \(\alpha + \beta i\) совпадает с корнем характеристического уравнения, то выражение для частного решения будет содержать дополнительный множитель \(x.\)

Неизвестные коэффициенты можно определить подстановкой найденного выражения для частного решения в исходное неоднородное дифференциальное уравнение.

Если правая часть неоднородного уравнения представляет собой сумму нескольких функций вида \[ <\left( x \right)>\;\;\text<и/или>>\;\; <\left[ <\left( x \right)\cos\left( <\beta x>\right) + \left( x \right)\sin\left( <\beta x>\right)> \right]>,> \] то частное решение дифференциального уравнения также будет являться суммой частных решений, построенных отдельно для каждого слагаемого в правой части.

Источник

ЛНДУ второго порядка с постоянными коэффициентами, примеры

,

где p и q – являются произвольными действительных чисел, а функция f(x) – непрерывна на интервале интегрирования X.

Выразим теорему, отображающая вид, в котором необходимо находить общее решение линейное неоднородное дифференциальное уравнение.

Общее решение на интервале X линейного неоднородного дифференциального уравнения: с непрерывными на интервале интегрирования X коэффициентами и непрерывной функцией f(x) равно сумме общего решения y₀ соответствующего линейного неоднородного дифференциального уравнения и любого частного решения исходного неоднородного уравнения, т.е., .

Значит, общим решением ЛНДУ 2-го порядка с постоянными коэффициентами оказывается сумма общего решения соответствующего линейного однородного дифференциального уравнения 2-го порядка с постоянными коэффициентами и частного решения исходного линейного неоднородного дифференциального уравнения: .

Вычисление y₀ расписано в статье линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами, сейчас рассмотрим метод нахождения .

Есть некоторые методы определения частного решения линейного неоднородного дифференциального уравнения 2-го порядка с постоянными коэффициентами. Эти методы определяются учитывая вид функции f(x), которая находится в правой части уравнения. Назовем их и в последующих статьях рассмотрим решения каждого ЛНДУ второго порядка с постоянными коэффициентами:

1. Если f(x) оказывается многочленом n-ой степени f(x) = Pn(x), то частное решение линейного неоднородного дифференциального уравнения находится как ,

где Qn(x) – многочлен степени n,

r – число корней характеристического уравнения, которые равны нулю.

Т.к. — является частным решением уравнения , тогда коэффициенты, которые определяют многочлен Qn(x), можно определить способом неопределенных коэффициентов из равенства .

2. Если функция f(x) представляется произведением многочлена степени n и экспоненты , значит, частное решение линейного неоднородного дифференциального уравнения второго порядка находится как ,

где Qn(x) является многочленом n-ой степени,

r – количество корней характеристического уравнения, которые равняются .

Коэффициенты многочлена Qn(x) можно определить из равенства .

3. Если функция f(x) выглядит так: , где А₁ и В₁ оказываются числами, значит, частное решение линейного неопределенного дифференциального уравнения представляют как ,

где А и В являются неопределенными коэффициентами,

4. Если , значит, ,

где r является числом комплексно сопряженных пар корней характеристического уравнения, которые равны ,

Найти коэффициенты многочленов Lm(x) и Nm(x) можно используя равенство .

5. Для всех остальных видов функции f(x) используется такой порядок действий:

,

а функции C₁(x) и C₂(x) определяют при дальнейшем интегрировании.

Источник

Дифференциальные уравнения второго порядка с правой частью специального вида

Если коэффициент P ₀ ( x ) ≠ 1, то на него можно поделить и после соответствующих переобозначений получить:

Примечание. Частным случаем (8.43) является линейное дифференциальное уравнение 2-го порядка с переменными коэффициентами:

Если в уравнении (8.43) f ( x ) ≡ 0, то оно называется однородным, если f ( x ) ≠ 0, то неоднородным.

Однородное дифференциальное уравнение, соответствующее неоднородному уравнению (8.43), имеет вид:

где c_i – константы интегрирования.

– также решение уравнений (8.45) и (8.46).

Рассмотрим одну из функций (8.48) – функцию y = e λx как решение для уравнения (8.46) с постоянными коэффициентами. Продифференцируем ее n раз:

Рассмотрим наиболее распространенный частный случай уравнения (8.46) – его аналог 2-го порядка:

Для данного уравнения характеристическое уравнение (8.50) принимает вид:

Уравнение (8.52) является квадратным относительно λ. В зависимости от дискриминанта D характеристического уравнения рассматривают три случая, приведенных в таблице 8.1.

Пример 8.17. Найти общее решение уравнений:

б) Составляем характеристическое уравнение λ 2 – 16 λ + 64 = 0.

Рассмотрим теперь линейное неоднородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами:

Теорема 8.4. Пусть задано линейное дифференциальное неоднородное уравнение второго порядка с постоянными коэффициентами и п равой частью специального вида

1. Если не является корнем характеристического уравнения соответствующего однородного уравнения, то частное решение уравнения (8.57) имеет вид:

где – многочлены общего вида (с неопределенными коэффициентами).

– многочлены общего вида

Рассмотрим в таблице 8.2 некоторые случаи составления частного решения линейного неоднородного дифференциального уравнения (8.57) по специальному виду его правой части.

является частным решением данного уравнения

Источник

7.1. Уравнения с правой частью специального вида

Рассмотрим неоднородное линейное дифференциальное уравнение с постоянными коэффициентами

, (7.1)

Где , , …, , – вещественные числа.

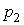
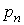
Уравнение (7.1) можно проинтегрировать рассмотренным ранее методом вариации произвольных постоянных, который сводится к составлению и решению системы линейных уравнений относительно функций, а также к интегрированию этих функций. Таких трудоемких операций можно избежать в некоторых случаях благодаря особому виду уравнения (7.1).

Поскольку общее решение соответствующего однородного уравнения (5.1) мы уже умеем находить, то получение общего решения уравнения (7.1) в силу теоремы подраздела 6.2 сводится к нахождению какого-нибудь частного его решения. Оказывается, что эта задача решается весьма просто при некоторых специальных видах функции 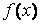в правой части уравнения (7.1). Далее рассматриваются следующие случаи.

1. Уравнения с правой частью в виде полинома.

В этом случае правая часть уравнения (7.1) представима в виде

,

Где – многочлен степени с известными коэффициентами.

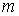
2. Правая часть в виде произведения полинома и экспоненты.

В данном случае правая часть уравнения (7.1) имеет вид

,

Где – многочлен степени с известными коэффициентами, – некоторое число.

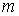
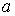
3. Правая часть в виде произведения полинома, экспоненты и гармонической функции.

В этом случае правая часть уравнения (7.1) имеет один из видов:

, ,

,

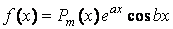
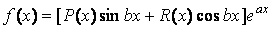
Где – многочлен степени с известными коэффициентами, и – многочлены известных степеней с известными коэффициентами, и – некоторые числа.

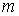
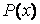
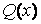
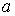
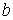
Для всех этих случаев на основании значений корней характеристического многочлена уравнения (7.1) и вида его правой части можно записать частное решение с точностью до коэффициентов входящих в него многочленов. Значения этих коэффициентов находятся путем составления и решения системы линейных алгебраических уравнений. Такой метод нахождения частного решения уравнения (7.1) называется Методом неопределенных коэффициентов.

Источник

Дифференциальные уравнения второго порядка с правой частью специального вида

Случай для линейного неоднородного дифференциального уравнения с постоянными коэффициентами и с правой частью имеющей вид полинома от x степени m

Для уравнения с постоянными коэффициентами в случае, когда правая часть имеет специальный вид, удается найти частное решение методом неопределенных коэффициентов (методом подбора частных решений).

Рассмотрим этот метод для уравнения n-го порядка вида

где a₁, …, a_n — действительные числа, α — действительное число, P_m (x) — полином от x степени m, которая может быть равной нулю, так что этот полином может вырождаться в число, отличное от нуля.

Метод неопределенных коэффициентов состоит в том, что задается вид частного решения с неопределенными коэффициентами, которые определяются подстановкой в данное уравнение. Вид частного решения уравнения зависит от того, совпадает ли число α с корнями характеристического уравнения:

где Q_m (x) — полином степени m с коэффициентами, подлежащими определению.

Случай для линейного неоднородного дифференциального уравнения с постоянными коэффициентами и с правой частью имеющей вид:

где α и b — действительные числа, P₁ и P₂ — полиномы от x, старшая степень которых равна m, так что один из них обязательно имеет степень m, а степень другого не превосходит m, и он может быть даже тождественно равен нулю.

Укажем вид частного решения уравнения (14.2) в двух случаях:

где Q₁ и Q₂ — полиномы степени m с неопределенными коэффициентами; причем надо брать оба эти полинома даже в том случае, когда один из полиномов P₁ и P₂ тождественно равен нулю.

f (x) = 8e3x ⇒ α = 3, β = 0, s = 0.
При этом число α ±βi = 3 не является корнем характеристического урав-
нения. Поэтому частное решение y

неоднородного уравнения надо искать
в виде

Источник