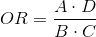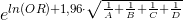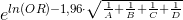доверительный интервал для отношения шансов

Блог странного учёного

Заметки о жизни и об исследованиях

25 жовт. 2009 р.

Расчёт и интерпретация отношения шансов

Отношение шансов (OR, odds ratio) — это широко используемый статистический показатель, позволяющий сравнивать частоту воздействия факторов риска в эпидемиологических исследованиях. Отношение шансов является ретроспективным сравнением влияния данного фактора риска на две группы лиц.

Термин « шанс » пришёл из азартных игр и означает отношение числа выигрышей к числу проигрышей или, другими словами, отношение числа случаев, когда событие наступило, к числу случаев, когда оно не наступило.

Расчёт отношения шансов

Расчёт отношения шансов для набора данных несложен: необходимо построить таблицу сопряжённости так, чтобы в первой строке стояла группа испытуемых, а в первом столбце — фактор риска.

Рассмотрим первый пример

Представьте, что Вы решили провести обследование мутации в гене X, предположительно вызывающего некую болезнь. Вы проанализировали гены однородных групп заболевших и здоровых и нашли, что распределение мутаций выглядит так (табл. 1):

Таблица 1.

Наличие мутации	Отсутствие мутации	Всего
Группа заболевших	A = 332	B = 164	496
Контрольная группа (оставшиеся здоровыми)	C = 230	D = 262	492
Всего	562	426	988

Сначала необходимо вычислить вероятность воздействия факторов риска (в данном случае, наличия мутации) в группе заболевших и в группе оставшихся здоровыми. Шанс того, что фактор риска есть в этих группах, рассчитывается так:

Шанс найти мутацию в группе заболевших = (A x (A + B))/(B x (A + B)) = A/B = 332/164 = 2.0244
Шанс найти мутацию в контрольной группе = (C x (C + D))/(D x (C + D)) = C/D = 230/262 = 0.8779

Затем следует найти OR путём деления шансов найти мутацию в группе заболевших и в контрольной группе:

OR = 2.0244/0.8779 = 2.306

Если свести все эти действия в одну формулу, то получим

OR = (A/B)/(C/D) = (А x D)/(В х С) = (332×262)/(164×230) = 2.306

. и это именно та формула, которая используется для определения OR.

Рассмотрим второй пример

Предположим, что в выборке из 100 мужчин 90 пили вино в предыдущую неделю, а в выборке из 100 женщин только 20 пили вино в тот же период (табл. 2).

Таблица 2.

Пили	Не пили	Всего
Мужчины	A = 90	B = 10	100
Женщины	C = 20	D = 80	100
Всего	110	90	200

Шанс мужчины быть в группе пивших вино 90:10 или 9:1, в то время как шанс женщины быть в группе пивших только 20:80 или 1:4 (0.25:1). Отношение шансов, таким образом, 9/0.25 = 36 показывает, что мужчины склонны гораздо чаще пить вино, чем женщины.

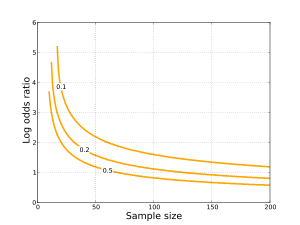
Расчет OR (воздействия фактора риска) является хорошим инструментом, но поскольку он основан на выборке, то он является не более чем оценкой. Точность этой оценки отчасти зависит от размера выборки, и, в целом, чем больше выборка, тем правдоподобнее оценка (хотя следует с большой осторожностью подходить к интерпретации OR в исследованиях с огромными размерами выборки). По этой причине кроме расчёта OR обычно вычисляют и стандартное отклонение (SE) с доверительным интервалом ( p ) 95%.

Есть несколько различных способов расчёта SE при заданном p для отношения шансов. Приведём один из них:

при p = 95% ln(SE) = 1.96(1/A + 1/B + 1/C + 1/D)^0.5

Для первого примера :

при p = 95% ln(SE) = 1.96(1/332 + 1/164 + 1/230 + 1/262)^0.5 = 0.25760567, соответственно

OR ± SE = от e^0.57790875 до e^0.25760567 или от 1.7823073 до 2.9835686

Для второго примера :

при p = 95% ln(SE) = 1.96(1/90 + 1/10 + 1/20 + 1/80)^0.5 = 0.817

В этих примерах доверительный интервал составляет 95%, но если нужно воспользоваться другой шириной доверительного интервала, то следует заменить 1.96 в уравнении соответствующим стандартным для нормального распределения значением.

Интерпретация отношения шансов

Предполагаемый фактор риска является значимым (т. е. с большой вероятностью вызовет наступление события, напр. болезнь), если OR больше единицы.

Следует иметь в виду, что само по себе значение OR нечувствительно к размеру выборки (напр., если во втором примере мы используем вдесятеро меньшие значения, то тоже получим OR = 36), однако от размера выборки зависит размер стандартного отклонения (так, во втором примере при вдесятеро меньших значениях мы вместо 2.26 получим SE = 13, т. е. ошибка измерения составит 37%).

Источник

СОДЕРЖАНИЕ

Определение и основные свойства

Убедительный пример в контексте предположения о редком заболевании

Определение с точки зрения групповых шансов

Определение в терминах совместной и условной вероятностей

Таким образом, отношение шансов

Симметрия

мы получили бы тот же результат

Отношение к статистической независимости

Если X и Y независимы, их совместные вероятности могут быть выражены через их предельные вероятности p _x = P ( X = 1) и p _y = P ( Y = 1) следующим образом

Восстановление вероятностей ячеек из отношения шансов и предельных вероятностей

Пример

Предположим, что в выборке из 100 мужчин 90 пили вино на предыдущей неделе (значит, 10 не пили), в то время как в выборке из 80 женщин только 20 пили вино за тот же период (то есть 60 не пили). Это формирует таблицу непредвиденных обстоятельств:

Отношение шансов (OR) можно напрямую рассчитать из этой таблицы как:

В качестве альтернативы, шансы мужчины, пьющего вино, составляют 90 к 10, или 9: 1, в то время как шансы женщины, пьющей вино, составляют всего 20 к 60, или 1: 3 = 0,33. Соотношение шансов, таким образом, составляет 9 / 0,33, или 27, что показывает, что мужчины гораздо чаще пьют вино, чем женщины. Подробный расчет:

Статистические выводы

Было разработано несколько подходов к статистическому выводу для отношений шансов.

Один из подходов к выводу использует приближения большой выборки к выборочному распределению логарифмического отношения шансов ( натуральный логарифм отношения шансов). Если мы используем обозначение совместной вероятности, определенное выше, логарифмическое отношение шансов популяции будет

то вероятности в совместном распределении можно оценить как

L знак равно бревно ⁡ ( п ^ 11 п ^ 00 п ^ 10 п ^ 01 ) знак равно бревно ⁡ ( п 11 п 00 п 10 п 01 ) <\ displaystyle > _ <11><\ hat

> _ <00>> <<\ hat

> _ <10>) <\ hat

> _ <01>>> \ right) = \ log \ left ( <\ dfrac n_ <00>> n_ <01>>> \ right)> > .

Распределение логарифмического отношения шансов приблизительно нормальное при:

Стандартная ошибка для логарифмического отношения шансов приблизительно

S E знак равно 1 п 11 + 1 п 10 + 1 п 01 + 1 п 00 <\ displaystyle <<\ rm > = <\ sqrt <<\ dfrac <1>>> + <\ dfrac <1>>> + <\ dfrac <1>) >> + <\ dfrac <1>>>>>>> .

Роль в логистической регрессии

Нечувствительность к типу отбора проб

Этот факт используется в двух важных ситуациях:

В обеих этих настройках отношение шансов может быть рассчитано на основе выбранной выборки без смещения результатов по сравнению с тем, что было бы получено для выборки населения.

Использование в количественных исследованиях

Отношение к относительному риску

Если доступен абсолютный риск в неэкспонированной группе, конверсия между ними рассчитывается следующим образом:

Если предположение о редком заболевании неприменимо, отношение шансов может сильно отличаться от относительного риска и вводить в заблуждение.

Рассмотрим уровень смертности пассажиров-мужчин и женщин, когда затонул Титаник. Из 462 женщин 154 умерли и 308 выжили. Из 851 мужчины 709 умерли, 142 выжили. Очевидно, что у мужчины на «Титанике» больше шансов умереть, чем у женщины, но насколько больше? Поскольку более половины пассажиров погибли, предположение о редкой болезни сильно нарушается.

Чтобы вычислить отношение шансов, обратите внимание, что для женщин шансы умереть были 1: 2 (154/308). У мужчин шансы были 5 к 1 (709/142). Отношение шансов составляет 9,99 (4,99 / 0,5). У мужчин в десять раз больше шансов умереть, чем у женщин.

Для женщин вероятность смерти составила 33% (154/462). Для мужчин вероятность составила 83% (709/851). Относительный риск смерти составляет 2,5 (0,83 / 0,33). Вероятность смерти мужчины в 2,5 раза выше, чем у женщины.

Какое число правильно представляет, насколько опаснее было находиться на Титанике? Относительный риск имеет то преимущество, что его легче понять и лучше представить, как думают люди.

Замешательство и преувеличение

В медицинской литературе отношение шансов часто путают с относительным риском. Для нестатистиков понятие отношения шансов является трудным для понимания, и оно дает более впечатляющую цифру для эффекта. Однако большинство авторов считают, что относительный риск легко понять. В одном исследовании члены национального фонда борьбы с болезнями на самом деле были в 3,5 раза чаще, чем не члены, слышали об общем лечении этого заболевания, но отношение шансов составляло 24, и в документе говорилось, что члены были более чем в 20 раз более вероятны. слышать о лечении. Исследование статей, опубликованных в двух журналах, показало, что 26% статей, в которых использовалось отношение шансов, интерпретировали его как отношение рисков.

Это может отражать простой процесс, когда непонимающие авторы выбирают наиболее впечатляющую и пригодную для публикации фигуру. Но в некоторых случаях его использование может быть заведомо вводящим в заблуждение. Было высказано предположение, что отношение шансов следует представлять как меру величины эффекта только в том случае, если отношение рисков невозможно оценить напрямую.

Обратимость и инвариантность

Это снова то, что называется «инвариантностью отношения шансов», и почему RR для выживания не то же самое, что RR для риска, в то время как OR имеет это симметричное свойство при анализе либо выживаемости, либо неблагоприятного риска. Опасность клинической интерпретации OR возникает, когда частота нежелательных явлений не является редкой, что приводит к преувеличению различий, когда предположение OR редкого заболевания не выполняется. С другой стороны, когда заболевание встречается редко, использование RR для выживаемости (например, RR = 0,9796 из приведенного выше примера) может клинически скрыть и скрыть важное удвоение неблагоприятного риска, связанного с лекарством или воздействием.

Оценщики отношения шансов

Отношение шансов выборки

Альтернативные оценщики

Числовые примеры

Следующие четыре таблицы непредвиденных обстоятельств содержат наблюдаемое количество клеток, а также соответствующее отношение шансов выборки ( OR ) и отношение шансов журнала выборки ( LOR ):

Следующие совместные распределения вероятностей содержат вероятности ячеек популяции, а также соответствующее отношение шансов популяции ( OR ) и логарифмическое отношение шансов популяции ( LOR ):

Числовой пример

Связанная статистика

Источник

Основные термины и понятия медицинской статистики

В данной статье мы приведем некоторые ключевые понятия статистики, актуальные при проведении медицинских исследований. Более подробно термины разбираются в соответствующих статьях.

Вариация

Определение. Степень рассеяния данных (значений признака) по области значений

Вероятность

Определение. Вероятность(probability) – степень возможности проявления какого – либо определённого события в тех или иных условиях.

Пример. Поясним определение термина на предложении «Вероятность выздоровления при применении лекарственного препарата Aримидекс равна 70%». Событием является «выздоровление больного», условием «больной принимает Аримидекс», степенью возможности – 70% (грубо говоря, из 100 человек, принимающих Аримидекс, выздоравливают 70).

Кумулятивная вероятность

Определение. Кумулятивная вероятность выживания (Cumulative Probability of surviving) в момент времени t – это то же самое, что доля выживших пациентов к этому моменту времени.

Пример. Если говорится, что кумулятивная вероятность выживания после проведения пятилетнего курса лечения равна 0.7, то это значит, что из рассматриваемой группы пациентов в живых осталось 70% от начального количества, а 30% умерло. Другими словами, из каждой сотни человек 30 умерло в течение первых 5 лет.

Время до события

Определение. Время до события – это время, выраженное в некоторых единицах, прошедшее с некоторого начального момента времени до наступления некоторого события.

Пояснение. В качестве единиц времени в медицинских исследованиях выступают дни, месяцы и годы.

Типичные примеры начальных моментов времени:

начало наблюдения за пациентом

проведение хирургического лечения

Типичные примеры рассматриваемых событий:

Выборка

Определение. Часть популяции, полученная путем отбора.

По результатам анализа выборки делают выводы о всей популяции, что правомерно только в случае, если отбор был случайным. Поскольку случайный отбор из популяции осуществить практически невозможно, следует стремиться к тому, чтобы выборка была по крайней мере репрезентативна по отношению к популяции.

Зависимые и независимые выборки

Определение. Выборки, в которые объекты исследования набирались независимо друг от друга. Альтернатива независимым выборкам – зависимые (связные, парные) выборки.

Гипотеза

Двусторонняя и односторонняя гипотезы

Сначала поясним применение термина гипотеза в статистике.

Для предания строгости исследования, проверяемое утверждение выражают математически. Например, если А – это количество лет, которое проживёт пациент, принимающий Аримидекс, а Т –это количество лет, которое проживёт пациент, принимающий Тамоксифен, то проверяемую гипотезу можно записать как А>Т.

Определение. Гипотеза называется двусторонней (2-sided), если она состоит в равенстве двух величин.

Пример двусторонней гипотезы: A=T.

Определение. Гипотеза называется односторонней (1-sided),если она состоит в неравенстве двух величин.

Примеры односторонних гипотез:

Дихотомические (бинарные) данные

Определение. Данные, выражаемые только двумя допустимыми альтернативными значениями

Доверительный интервал

Обозначение. Очень часто используются сокращение: ДИ 95 % (CI 95%) – это доверительный интервал с уровнем доверия 95%.

Достоверность, статистическая значимость (P – уровень)

Определение. Статистическая значимость результата – это мера уверенности в его «истинности».

Любое исследование проходит на основе лишь части объектов. Исследование эффективности лекарственного препарата проводится на основе не вообще всех больных на планете, а лишь некоторой группы пациентов (провести анализ на основе всех больных просто невозможно).

Предположим, что в результате анализа был сделан некоторый вывод (например, использование в качестве адекватной терапии препарата Аримидекс в 2 раза эффективнее, чем препарата Тамоксифен).

Вопрос, который необходимо при этом задавать: «Насколько можно доверять этому результату?».

Представьте, что мы проводили исследование на основе только двух пациентов. Конечно же, в этом случае к результатам нужно относиться с опасением. Если же были обследовано большое количество больных (численное значение «большого количества» зависит от ситуации), то сделанным выводам уже можно доверять.

Так вот, степень доверия и определяется значением p-уровня (p-value).

Более высокий p- уровень соответствует более низкому уровню доверия к результатам, полученным при анализе выборки. Например, p- уровень, равный 0.05 (5%) показывает, что сделанный при анализе некоторой группы вывод является лишь случайной особенностью этих объектов с вероятностью только 5%.

Другими словами, с очень большой вероятностью (95%) вывод можно распространить на все объекты.

Во многих исследованиях 5% рассматривается как приемлемое значение p-уровня. Это значит, что если, например, p= 0.01, то результатам доверять можно, а если p=0.06, то нельзя.

Исследование

Проспективное исследование – это исследование, в котором выборки выделяются на основе исходного фактора, а в выборках анализируется некоторый результирующий фактор.

Ретроспективное исследование – это исследование, в котором выборки выделяются на основе результирующего фактора, а в выборках анализируется некоторый исходный фактор.

Если мы набираем 2 выборки, в одной – матери моложе 20 лет, в другой – старше, а затем анализируем массу детей в каждой группе, то это проспективное исследование.

Если мы набираем 2 выборки, в одной – матери, родившие детей легче 2,5 кг, в другой – тяжелее, а затем анализируем возраст матерей в каждой группе, то это ретроспективное исследование (естественно, такое исследование можно провести, только когда опыт закончен, т.е. все дети родились).

Исход

Определение. Клинически значимое явление, лабораторный показатель или признак, который служит объектом интереса исследователя. При проведении клинических испытаний исходы служат критериями оценки эффективности лечебного или профилактического воздействия.

Клиническая эпидемиология

Определение. Наука, позволяющая осуществлять прогнозирование того или иного исхода для каждого конкретного больного на основании изучения клинического течения болезни в аналогичных случаях с использованием строгих научных методов изучения больных для обеспечения точности прогнозов.

Когорта

Определение. Группа участников исследования, объединенных каким-либо общим признаком в момент ее формирования и исследуемых на протяжении длительного периода времени.

Контроль

Контроль исторический

Определение. Контрольная группа, сформированная и обследованная в период, предшествующий исследованию.

Контроль параллельный

Определение. Контрольная группа, формируемая одновременно с формированием основной группы.

Корреляция

Определение. Статистическая связь двух признаков (количественных или порядковых), показывающая, что большему значению одного признака в определенной части случаев соответствует большее – в случае положительной (прямой) корреляции – значение другого признака или меньшее значение – в случае отрицательной (обратной) корреляции.

Пример. Между уровнем тромбоцитов и лейкоцитов в крови пациента обнаружена значимая корреляция. Коэффициент корреляции равен 0,76.

Коэффициент риска (КР)

Определение. Коэффициент риска (hazard ratio) – это отношение вероятности наступления некоторого («нехорошего») события для первой группы объектов к вероятности наступления этого же события для второй группы объектов.

Пример. Если вероятность появления рака лёгких у некурящих равна 20%, а у курильщиков – 100%, то КР будет равен одной пятой. В этом примере первой группой объектов являются некурящие люди, второй группой – курящие, а в качестве «нехорошего» события рассматривается возникновение рака лёгких.

Интерпретация значения величины. Очевидно, что:

1) если КР=1, то вероятность наступления события в группах одинаковая

2) если КР>1, то событие чаще происходит с объектами из первой группы, чем из второй

3) если КР 1, то вероятность наступления события больше вероятности того, что событие не произойдёт;

3) если Шанс 1, то шанс для первой группы больше шанса для второй группы

Источник

Библиотека постов MEDSTATISTIC об анализе медицинских данных

Ещё больше полезной информации в нашем блоге в Инстаграм @medstatistic

Критерии и методы

ОТНОШЕНИЕ ШАНСОВ

1. История разработки показателя отношения шансов

2. Для чего используется показатель отношения шансов?

Отношение шансов позволяет оценить связь между определенным исходом и фактором риска.

Отношение шансов позволяет сравнить группы исследуемых по частоте выявления определенного исхода. Важно, что результатом применения отношения шансов является не только определение статистической значимости связи между фактором и исходом, но и ее количественная оценка.

Отношение шансов при сравнении двух групп рассчитывается как частное от деления шансов развития исхода в основной группе к шансам развития исхода в контрольной группе. В свою очередь, шансами называют отношение числа исследуемых с наличием исхода к числу исследуемых с отсутствием исхода. Также для рассчитанного ОШ рассчитывается 95% доверительный интервал (95% ДИ).

3. Условия и ограничения применения отношения шансов

4. Как рассчитать отношение шансов?

Отношение шансов – это значение дроби, в числителе которой, находятся шансы определённого события для первой группы, а в знаменателе шансы того же события для второй группы.

Шансом является отношение числа исследуемых, имеющих определенный признак (исход или фактор), к числу исследуемых, у которых данный признак отсутствует.

Например, была отобрана группа пациентов, прооперированных по поводу панкреонекроза, число которых составило 100 человек. Через 5 лет из их числа в живых осталось 80 человек. Соответственно, шанс выжить составил 80 к 20, или 4.

Удобным способом является расчёт отношения шансов со сведением данных в таблицу 2х2:

Исход есть (1)	Исхода нет (0)	Всего
Фактор риска есть (1)	A	B	A + B
Фактор риска отсутствует (0)	C	D	C + D
Всего	A + C	B + D	A + B + C + D

Для данной таблицы отношение шансов рассчитывается по следующей формуле:

Очень важно оценить статистическую значимость выявленной связи между исходом и фактором риска. Связано это с тем, что даже при невысоких значениях отношения шансов, близких к единице, связь, тем не менее, может оказаться существенной и должна учитываться в статистических выводах. И наоборот, при больших значениях OR, показатель оказывается статистически незначимым, и, следовательно, выявленной связью можно пренебречь.

Для оценки значимости отношения шансов рассчитываются границы 95% доверительного интервала (используется абрревиатура 95% ДИ или 95% CI от англ. «confidence interval»). Формула для нахождения значения верхней границы 95% CI:

Формула для нахождения значения нижней границы 95% CI:

5. Как интерпретировать значение отношения шансов?

Дополнительно в каждом случае обязательно оценивается статистическая значимость отношения шансов исходя из значений 95% доверительного интервала.

6. Пример расчета показателя отношения шансов

1. Составим четырехпольную таблицу сопряженности:

ВПР плода диагностирован	ВПР плода отсутствует	Всего
Курящие	50 (А)	10 (В)	60
Некурящие	150 (С)	90 (D)	240
Всего	200	100	300

2. Рассчитаем значение отношения шансов:

OR = (A * D) / (B * C) = (50 * 90) / (150 * 10) = 3.

Таким образом, исследование показало, что шансы встретить курящую женщину среди пациенток с диагностированным ВПР плода в 3 раза выше, чем среди женщин без признаков ВПР плода. Наблюдаемая зависимость является статистически значимой, так как 95% CI не включает 1, значения его нижней и верхней границ больше 1.

Источник