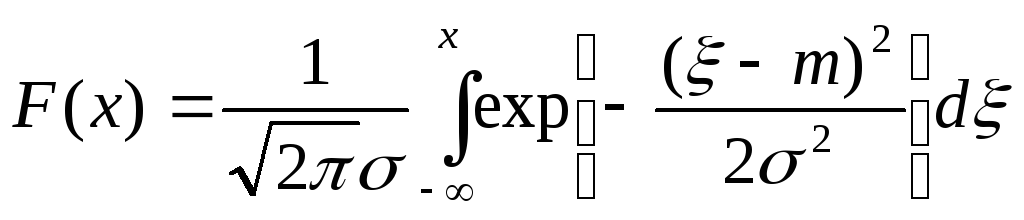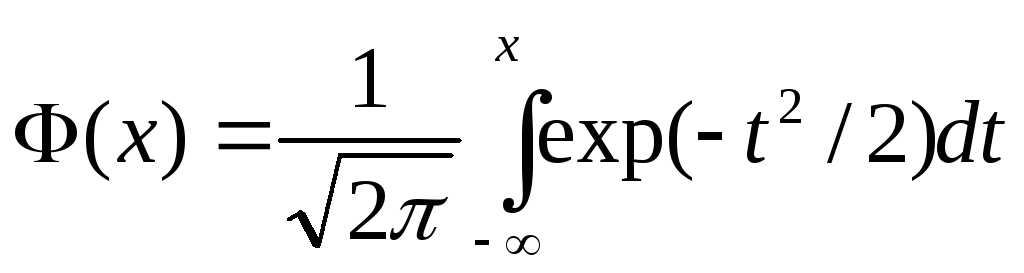гауссов шум случайный сигнал у которого имеет форму гауссовой кривой

Аддитивный белый гауссов шум

Аддитивным белым гауссовским шумом называется вид мешающего воздействия, которое наблюдается в канале передачи данных.

Для такого шума характерны:

Нормальное распределение называют еще распределением Гаусса – это распределение вероятностей, для одномерного случая задающееся функцией, которая совпадает с гауссовской.

Функция Гаусса зависит от двух параметров:

1) математического ожидания (μ);

2) стандартного отклонения (σ).

В случае стандартного нормального распределения первый параметр равен нулю, второй – единице.

К аддитивному относится способ воздействия, при котором белый шум и полезный сигнал суммируются. Такой шум является наиболее распространенным для использования в расчетах и моделировании систем радиочастотной связи. Его противоположностью можно назвать такой шум, как мультипликативный, который с полезным сигналом не суммируется, а перемножается.

Гауссов шум и белый шум

Иногда гауссовский шум ошибочно считают обязательно белым. Но эти два понятия эквивалентными не являются.

Для гауссова шума характерно нормальное распределение значений сигнала, а вот термин «белый шум» относится к корреляции сигнала в два разных момента времени. При этом данная корреляция от распределения амплитуды шума не зависит.

Другими словами, белый шум распределение может иметь любое: Гаусса, Пуассона, Коши и др.

Название «белый» шум получил от белого света, который содержит электромагнитные волны частот всего видимого диапазона электромагнитного излучения.

«Чисто» белый шум, то есть с одинаковой спектральной мощностью на всех частотах, в природе и технике не встречается. Иначе сигнал имел бы бесконечную мощность. Но под категорию белых попадают любые шумы с одинаковой (или слабо отличающейся) спектральной плотностью в рассматриваемом частотном диапазоне.

Применение

В физике и технике белый шум активно применятся. Например, в архитектурной акустике с целью сокрытия нежелательных шумов внутри зданий генерируют постоянный низкоамплитудный белый шум. Или еще он используется для измерения частотных характеристик разнообразных линейных динамических систем: усилителей, электронных фильтров, дискретных систем управления и т. д. Когда на вход такой системы подается белый шум, то на выходе получается сигнал, который является откликом системы на это приложенное воздействие.

Источник

15 Белый шум и его свойства. Гауссовский случайный процесс.

стационарный случайный процесс с постоянной на всех частотах спектральной плотностью мощности называется белым шумом.

(7.1)

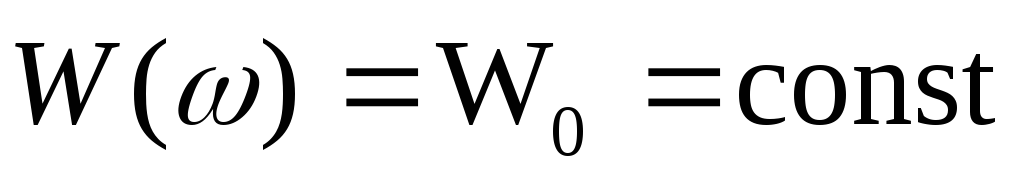
По теореме Винера-Хинчина функция корреляции белого шума:

равна нулю всюду кроме точки . Средняя мощность (дисперсия) белого шума неограниченно велика.

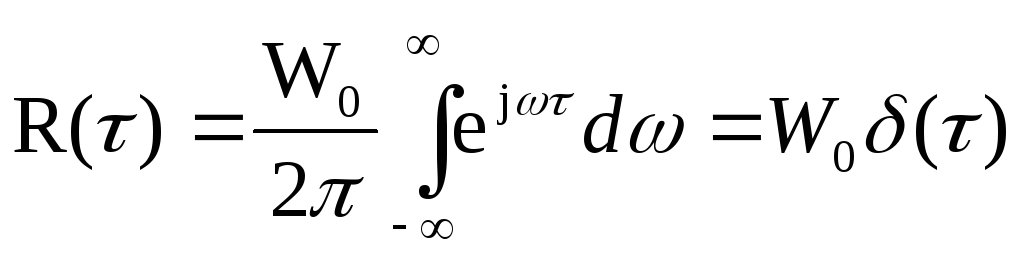
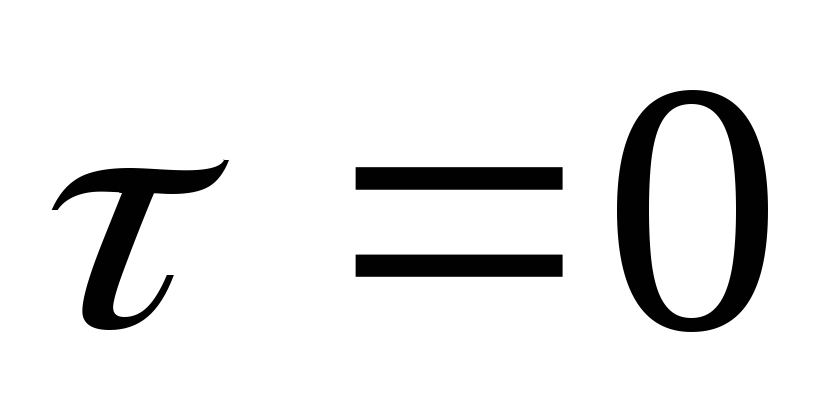
Белый шум является дельта-коррелированным процессом. Некоррелированность мгновенных значений такого случайного сигнала означает бесконечно большую скорость изменения их во времени – как бы мал ни был интервал , сигнал за это время может измениться на любую наперёд заданную величину.

Белый шум является абстрактной математической моделью и отвечающий ему физический процесс, безусловно, не существует в природе. Однако это не мешает приближённо заменять реальные достаточно широкополосные случайные процессы белым шумом в тех случаях, когда полоса пропускания цепи, на которую воздействует случайный сигнал, оказывается существенно уже эффективной ширины спектра шума.

Б) Гауссово (нормальное) распределение.

В теории случайных сигналов фундаментальное значение имеет гауссова плотность вероятности.

(7.2)

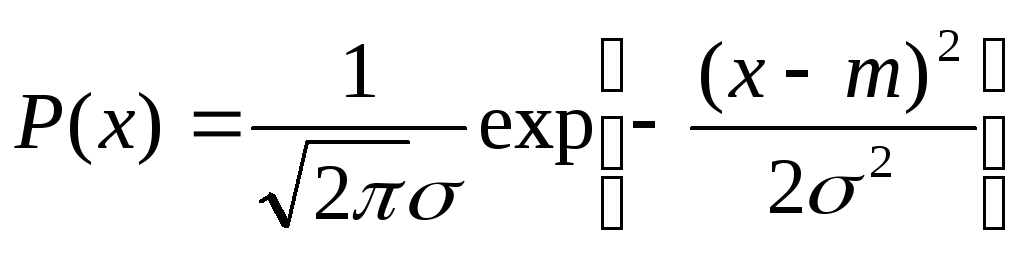
содержащая два числовых параметра m и

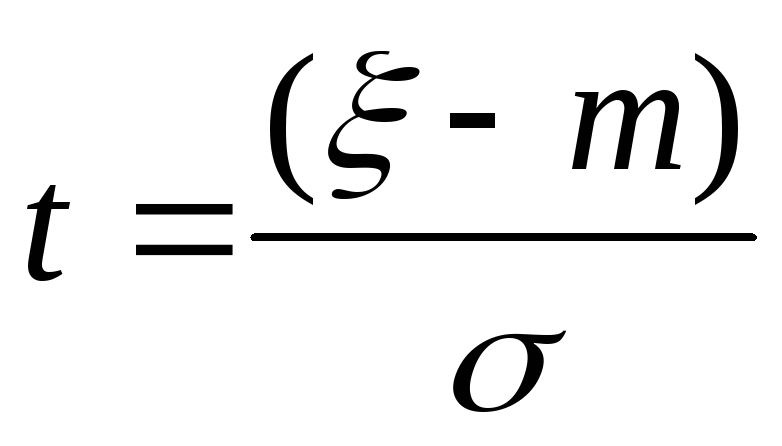
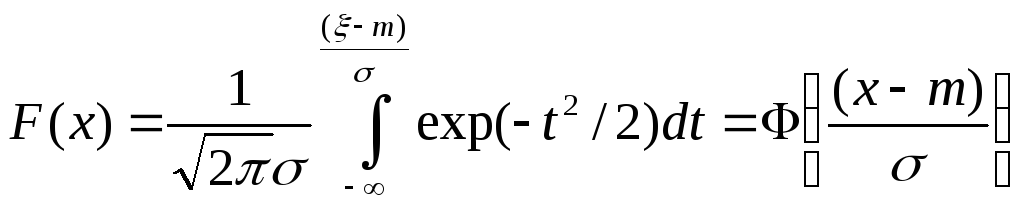
Замена переменной даёт:

(7.3)

Здесь Ф интеграл вероятностей

График функции F(x) имеет вид монотонной кривой, изменяющейся от 0 до 1.

16.. Узкополосный случайный процесс. Распределение Рэлея. Закон Релея-Райса.

Исследуем свойства узкополосных случайных сигналов, у которых спектральная плотность мощности имеет резко выраженный максимум вблизи некоторой частоты , отличной от нуля. Определим функцию корреляции узкополосного случайного процесса.

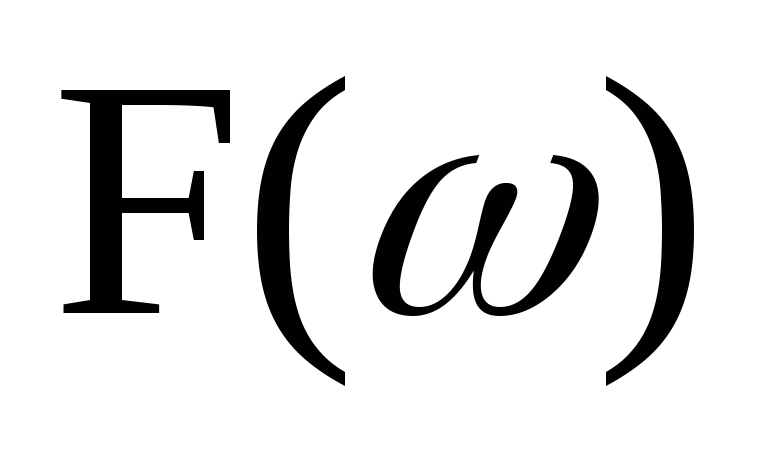
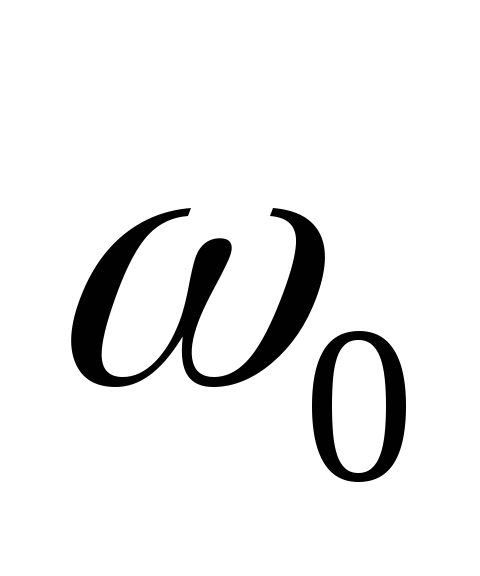
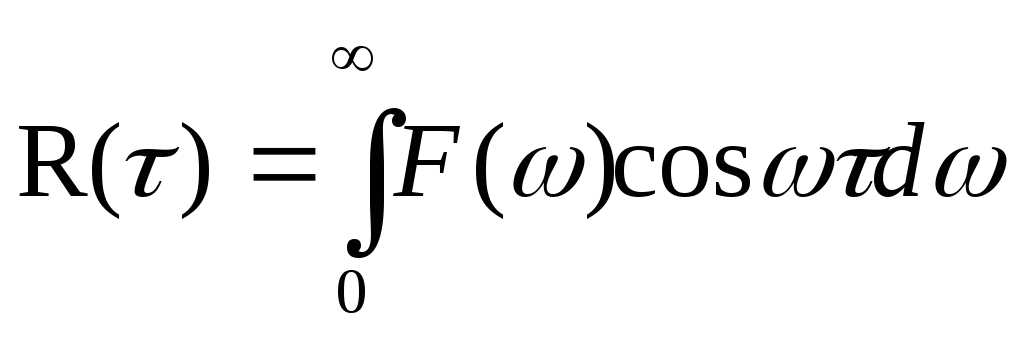
Рассмотрим стационарный случайный процесс x(t), односторонний спектр мощности которого концентрируется в окрестности некоторой частоты>0. По теореме Винера-Хинчина функция корреляции данного процесса

(7.4)

сместим спектр процесса из окрестности частоты в окрестность нулевой частоты,(7.5)

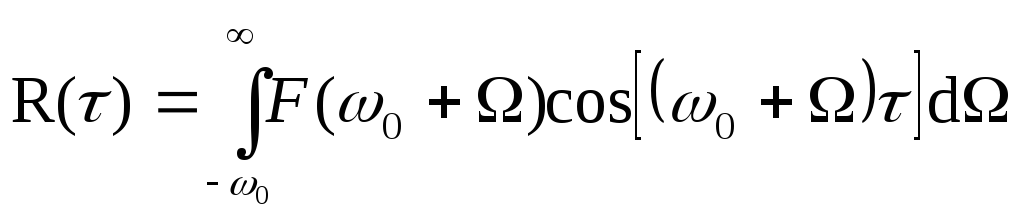
Проводя усреднение с помощью плотности вероятности (7.22) находим среднее значение огибающей и её дисперсию:

(7.23)

(7.24)

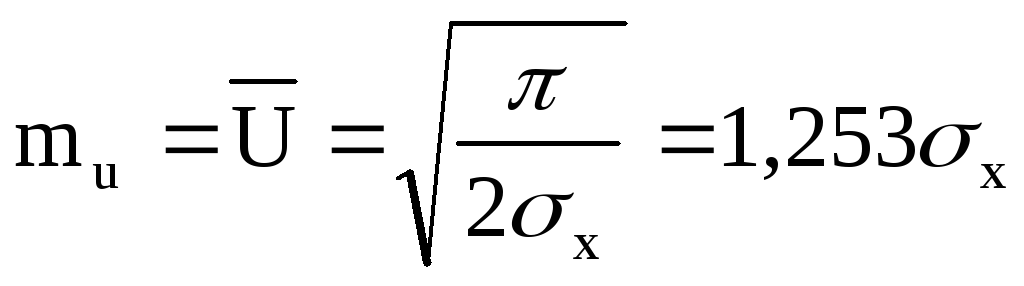
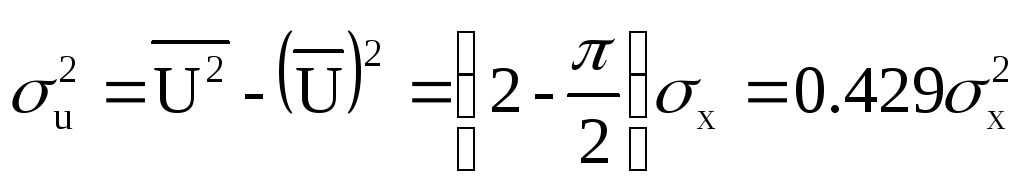
Располагая одномерной плотностью вероятности огибающей, можно решить ряд задач теории узкополосных случайных процессов, в частности, найти вероятность превышения огибающей некоторого заданного уровня.

Случайные величины, распределенные по закону Рэлея,

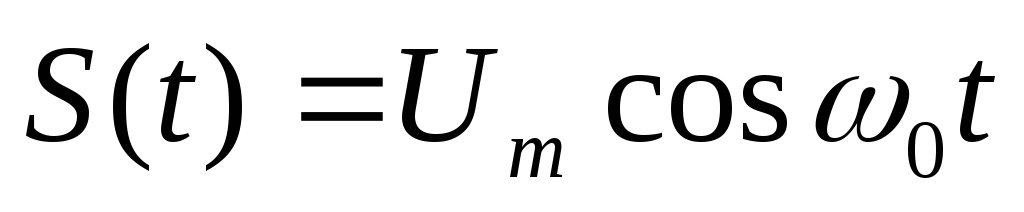
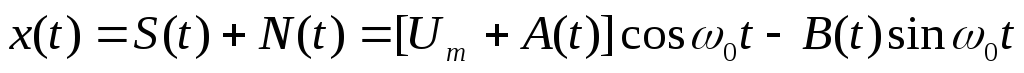
Простейшей задачей является нахождение одномерной плотности вероятности огибающей суммарного колебания. Считая, что полезный сигнал , в то время как шум, запишем выражение реализации суммарного процессаX(t) . Данный случайный процесс узкополосен, поэтому его реализация может быть выражена посредством медленно меняющихся огибающейU(t) и начальной фазы :

В новых переменных имеем.

(7.26)

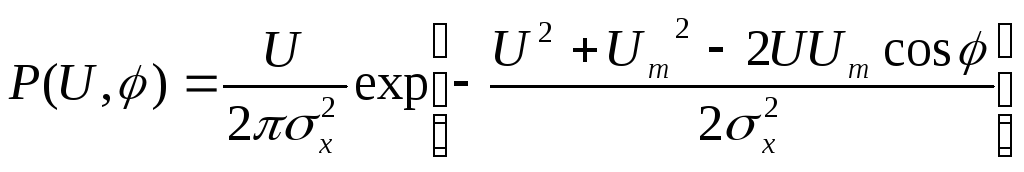
Теперь чтобы получить одномерную плотность вероятности огибающей, следует проинтегрировать правую часть формулы (7.26) по угловой координате в результате чего находим:

(7.27)

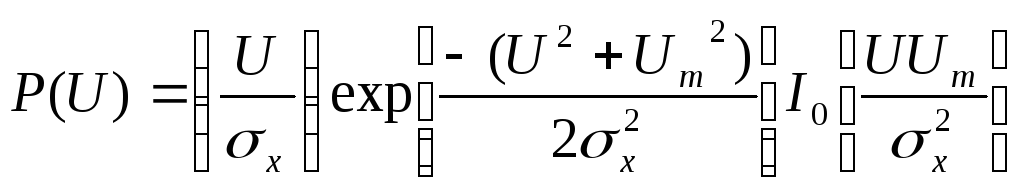
Данная формула выражает закон, получивший название закона Райса. Отметим, что при , т.е. в отсутствие детерминированного сигнала, закон Райса переходит в закон Рэлея.

Подставив это выражение в (7.27), имеем

(7.28)

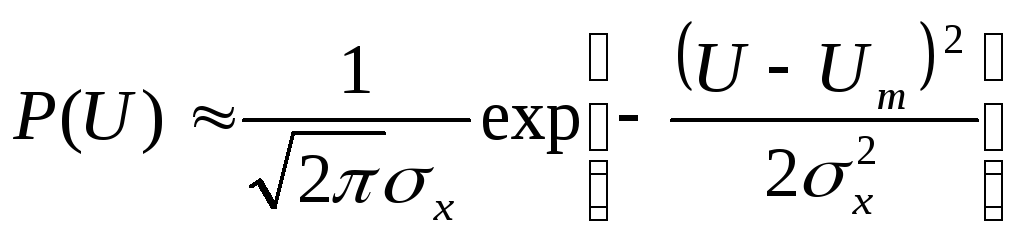
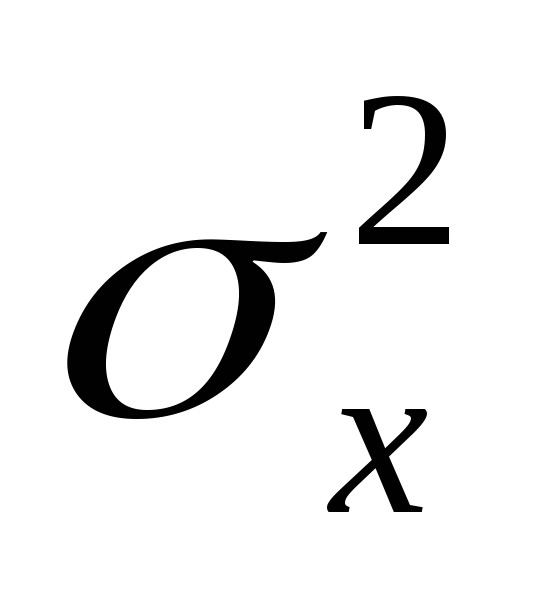
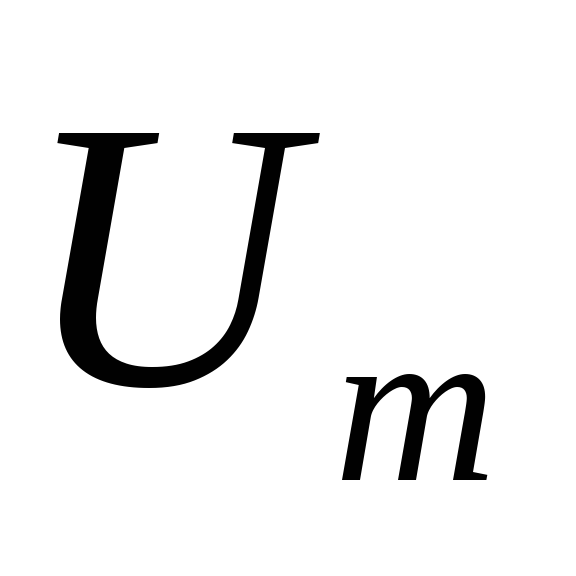
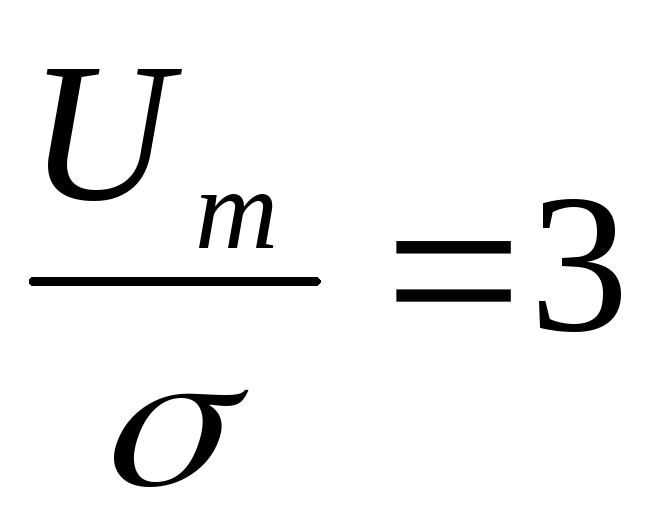
Т.е. огибающая результирующего сигнала распределена в этом случае приближённо нормально с дисперсией и математическим ожиданием. Практически считают, что уже приогибающая результирующего сигнала нормализуется.

Источник

Документация

Этот пример обсуждает обнаружение детерминированного сигнала в комплексном, белом, Гауссовом шуме. С этой ситуацией часто сталкиваются в радаре, гидролокаторе и коммуникационных приложениях.

Обзор

В этом примере мы ограничиваем наше обсуждение сценарием, где сигнал детерминирован, и шум является белым и Гауссов распределенный. Оба сигнала и шум являются комплексными.

Пример обсуждает следующие темы и их взаимосвязи: когерентное обнаружение, некогерентное обнаружение, согласованная фильтрация и кривые рабочей характеристики приемника (ROC).

И шумовая модель сигнала

Полученный сигнал принят, чтобы следовать модели

x ( t ) = s ( t ) + n ( t )

где s (t) является сигналом, и n (t) является шумом. Не теряя общность, мы принимаем, что степень сигнала равна 1 ватту, и шумовая мощность определяется соответственно на основе сигнала к шумовому отношению (ОСШ). Например, для ОСШ 10 дБ, шумовой мощности, i.e., шумовое отклонение составит 0,1 ватта.

Согласованный фильтр

Согласованный фильтр часто используется во фронтэнде приемника, чтобы улучшить ОСШ. С дискретной точки зрения сигнала коэффициенты согласованного фильтра просто даны спрягаемыми инвертированными выборками комплекса сигнала.

Детектор

Целевая функция правила решения NP может быть записана как

затем упрощенный детектор становится

Одно демонстрационное обнаружение Используя когерентный приемник

Мы сначала исследуем пример обнаружения сигнала в шуме, использующем всего одну выборку.

Примите, что сигнал является модульной выборкой степени, и ОСШ составляет 3 дБ. Используя симуляцию Монте-Карло с 100000 испытаниями, мы генерируем сигнал и шум как

Обратите внимание на то, что шум является комплексным, белым и Гауссов распределенный.

Если полученный сигнал содержит цель, им дают

Согласованный фильтр в этом случае тривиален, поскольку сам сигнал является модульной выборкой.

В этом случае усиление согласованного фильтра равняется 1, поэтому, нет никакого усиления ОСШ.

Теперь мы делаем обнаружение и исследуем эффективность детектора. Для когерентного приемника полученный сигнал после того, как согласованным фильтром дают

Достаточная статистика, i.e., значение раньше выдерживало сравнение с порогом обнаружения, поскольку когерентный детектор является действительной частью полученного сигнала после согласованного фильтра, i.e.,

где порог T связан с PFA как

В уравнении N является степенью сигнала, и M является усилением согласованного фильтра. Обратите внимание на то, что T является порогом сигнала после согласованного фильтра, и NM представляет шумовую мощность после согласованного фильтра, таким образом, T N M может быть рассмотрен как отношение между и шумовой величиной сигнала, i.e., это связано с сигналом к шумовому отношению, ОСШ. Поскольку ОСШ обычно упоминается как отношение между и шумовой мощностью сигнала, рассматривая модули каждой величины в этом выражении, мы видим это

Поскольку N и M фиксируются, если шумовая и форма волны сигнала выбрана, существует соответствие между T и ОСШ. Данный T является порогом сигнала, ОСШ может быть рассмотрен как порог сигнала к шумовому отношению. Поэтому пороговое уравнение может затем быть переписано в форме

Необходимый порог ОСШ, учитывая комплекс, белый Гауссов шум для детектора NP может быть вычислен с помощью функции npwgnthresh можно следующим образом:

Обратите внимание на то, что этот порог, несмотря на то, что также в форме значения ОСШ, отличается от ОСШ полученного сигнала. Пороговый ОСШ является расчетным значением на основе желаемой эффективности обнаружения, в этом случае PFA ; в то время как полученный ОСШ сигнала является физическими характеристиками сигнала, определенного средой распространения, формой волны, степенью передачи, и т.д.

Истинный порог T может затем быть выведен из этого порога ОСШ как

который удовлетворяет наше требование.

Чтобы видеть отношение среди ОСШ, Pd и PFA в графике, мы можем построить теоретическую кривую ROC с помощью функции rocsnr для значения ОСШ 3 дБ как

Одно демонстрационное обнаружение Используя некогерентный приемник

Некогерентный приемник не знает фазу полученного сигнала, поэтому, для целевого данного случая, сигнал x содержит термин фазы и задан как

То, когда некогерентный приемник используется, количество раньше соответствовало порогу, является степенью (или величина) полученного сигнала после согласованного фильтра. В этой симуляции мы выбираем величину в качестве достаточной статистики.

Сигнал к шумовому пороговому ОСШ отношения для детектора NP может быть вычислен с помощью npwgnthresh можно следующим образом:

Снова, Pd может затем быть получен с помощью

Обратите внимание на то, что этот получившийся Pd является нижним к эффективности, которую мы получаем от когерентного приемника.

Для целевого отсутствующего случая полученный сигнал содержит только шум. Мы можем вычислить PFA с помощью симуляции Монте-Карло как

Кривая ROC для некогерентного приемника построена как

Мы видим, что эффективность некогерентного детектора приемника является нижней к тому из когерентного приемника.

Сводные данные

Обратите внимание на то, что порог ОСШ не может быть порогом, используемым непосредственно в фактическом детекторе. Фактический детектор обычно использует легкое, чтобы вычислить количество достаточной статистики, чтобы выполнить обнаружение. Таким образом истинный порог должен быть выведен из вышеупомянутого порога ОСШ соответственно так, чтобы это было сопоставимо с выбором достаточной статистики.

Этот пример выполняет обнаружение с помощью только одной полученной выборки сигнала. Следовательно, получившийся Pd является довольно низким и нет никакого усиления обработки, достигнутого согласованным фильтром. Чтобы улучшить Pd и использовать в своих интересах усиление обработки согласованного фильтра, мы можем использовать несколько выборок, или даже несколько импульсов, полученного сигнала. Для получения дополнительной информации о том, как обнаружить сигнал с помощью нескольких выборок или импульсов, обратитесь к Обнаружению Сигнала в качестве примера Используя Несколько Выборок.

Открытый пример

У вас есть модифицированная версия этого примера. Вы хотите открыть этот пример со своими редактированиями?

Источник

Модели случайных сигналов и помех

Нет ничего более противного разуму и постоянству природы, чем случайность.
Сам бог не может знать того, что произойдет случайно.
Ибо если знает, то это определенно произойдет,
а если определенно произойдет, то не случайно.
Марк Туллий Цицерон. О девинации.
Римский философ и политик, I в.д.н.э.

Наиболее распространенными моделями случайных сигналов и помех являются телеграфный сигнал, белый шум, гауссовский случайный процесс, гауссовский шум.

P(n) = ( a | t |) 2 exp(- a | t |)/n! (17.4.1)

R x ( t ) = M= c 2 (-1) n P(n) =

= c 2 exp(- a | t |)(-1) n ( a | t ) n /n! = c 2 exp(-2 a | t |). (17.4.2)

Интервал ковариации сигнала:

Двусторонняя спектральная плотность сигнала:

S x ( w ) =R x ( t ) exp(-j wt ) d t = a c 2 /( a 2 + w 2 ). (17.4.4)

Односторонняя спектральная плотность:

G x ( w )=2R x ( t ) exp(-j wt ) d t = 2 a c 2 /( a 2 + w 2 ). (17.4.5)

Ширина спектра телеграфного сигнала :

Отсюда следует, что спектр случайного процесса тем шире, чем меньше интервал ковариации процесса.

т.е. мощность белого шума и его дисперсия равны бесконечности, а значения шума не коррелированны для любых | t | № 0, так как корреляционная функция представляет собой идеальный дельта-импульс. Тем не менее многие помехи в радиотехнике, в технике связи и в других отраслях рассматривают как белый шум, если выполняется следующее соотношение между шириной спектров полезных сигналов и шумов

B k. сигнал / B k.шум

и спектральная плотность шумов слабо изменяется в интервале спектра сигнала.

Если частотный диапазон спектра, на котором рассматриваются сигналы и помехи, равен 0-В, то спектральная плотность шума задается в виде:

при этом корреляционная функция шума определяется выражением:

Эффективная шумовая ширина спектра:

B k = R x (0)/G x (f) max = B. (17.4.10)

Эффективное шумовое время ковариации:

T k = 2|R x ( t )|d t / R x (0). (17.4.11)

Реальное шумовое время ковариации целесообразно определить по ширине главного максимума функции R x ( t ), в котором сосредоточена основная часть энергии шумов, при этом T k = 1/В и B k T k = 1, т.е. соотношение неопределенности выполняется.

Как следует из всех этих выражений и наглядно видно на рис. 17.4.4, при ограничении частотного диапазона в шумах появляется определенная ковариация между значениями и чем меньше частотный диапазон шумов, тем больше их радиус ковариации. По существу, ограничение частотного диапазона шумов определенным диапазоном эквивалентно фильтрации белого шума частотным фильтром с соответствующей шириной полосы пропускания, при этом, в полном соответствии с выражением (17.3.7), корреляционная функция импульсного отклика фильтра переносится на шум.

Гауссовский шум возникает при суммировании статистически независимых белых шумов и имеет следующую функцию корреляции:

R x ( t ) = a exp(-2 ps 2 t 2 ). (17.4.12)

Спектральная плотность шумов:

Эффективные шумовые ширина спектра и время ковариации:

Соотношение неопределенности превращается в равенство: B k T k = 1/2.

Гауссовские случайные процессы преобладают в практических задачах. Случайный процесс x(t) называется гауссовским, если для любого набора фиксированных моментов времени t n случайные величины x(t n ) подчиняются многомерному нормальному распределению. Плотность вероятностей мгновенных значений x(t) эргодического гауссовского процесса определяется выражением:

Среднее значение и его оценка по достаточно большому интервалу Т:

m x = xp(x) dx, m x » (1/T)x(t) dt.

При нулевом среднем (или при центрировании функции x(t) для упрощения расчетов) дисперсия не зависит от t и равна:

s x 2 =x 2 p(x) dx.

Оценка дисперсии при больших Т:

s x 2 » (1/T)x 2 (t) dt =S x (f) df = 2S x (f) df =G x (f) df. (17.4.16)

Следовательно, плотность вероятностей гауссовского процесса полностью характеризуется спектральной плотностью, по которой можно определить значение дисперсии процесса. На вид спектральных плотностей и соответствующих им ковариационных функций никаких ограничений не накладывается.

2. Бендат Дж., Пирсол А. Прикладной анализ случайных данных. – М.: Мир, 1989. – 540 с.

25. Сергиенко А.Б. Цифровая обработка сигналов. – СПб.: Питер, 2003. – 608 с.

Источник

Слухи об отмене теоремы Котельникова сильно преувеличены

«Фильтруй перед дискретизацией!»

Эта мантра насмерть вбита в головы поколений студентов-инженеров. Здесь под «дискретизацией» подразумевается преобразование непрерывной функции времени в серию дискретных значений. Такой процесс происходит везде, где компьютер оцифровывает сигнал из реального аналогового мира. «Фильтровать» — значит удалять из сигнала высокочастотные составляющие. Поскольку этот процесс происходит в аналоговом мире, то требует реального аналогового оборудования: цепей из резисторов, конденсаторов и усилителей. Создание такой цепи может стать утомительным и трудоёмким процессом, например, если на электронных микросхемах не хватает места. Научная группа Шепарда рассмотрела это ограничение в контексте устройства для записи сигналов от нервных клеток.

Теперь авторы заявляют, что изобрели «парадигму сбора данных, которая не требует фильтров для защиты от наложения для каждого канала, тем самым преодолевая ограничения масштабирования существующих систем». По сути они говорят, что вместо аппаратных цепей можно использовать программное обеспечение, которое работает на цифровой стороне уже после дискретизации. «Ещё одним преимуществом такого подхода к сбору данных является то, что все шаги обработки сигнала (разделение каналов и удаление) реализованы в цифровом виде», сказано в научной работе.

Если это правда, то стало бы важнейшим открытием. Оно не только опровергает общепринятое мнение, которого придерживались почти столетие. Ешё и куча аппаратуры становится ненужной. Фильтры для защиты от наложения повсеместно используются в электронном оборудовании. В вашем мобильнике несколько цифровых радиочипов и аналого-цифровой преобразователь звуковых сигналов, а между ними с полдюжины микросхем для фильтров для защиты от наложения. Если можно заменить все эти электронные компоненты несколькими строками кода, то производители с радостью сделают это. Так что это потенциально идея на миллиард долларов.

К сожалению, это большая ошибка. Я покажу, что эти документы не имеют ничего общего с теоремой дискретизации. Они не отменяют обработку. И не отменяют аналоговые фильтры перед оцифровкой. И даже близко не приближаются к лучшим системам по извлечению нейронных сигналов из шума.

Почему наложение — это плохо

[пропустите эту часть, если знаете ответ]

Дискретизация — важнейший этап сбора данных, когда непрерывный сигнал превращается в дискретную серию чисел. Чаще всего непрерывный сигнал — это сигнал напряжения. Его дискретизирует и оцифровывает через равные промежутки времени электронная схема, которая называется «аналого-цифровой преобразователь» (рис. 1). На первый взгляд, из-за дискретизации теряется информация. Ведь на непрерывной кривой напряжения «бесконечно много» точек, но после дискретизации мы оставляем только их часть. Следовательно, потеряно бесконечное число точек между выбранными. И вот здесь звучит важнейшее утверждение теоремы дискретизации: в соответствующих условиях отдельные образцы содержат всю информацию, необходимую для идеального восстановления непрерывной функции напряжения, которая их произвела. В этом случае нет потери информации из-за дискретизации.

Эти соответствующие условия просты: входной сигнал должен изменяться достаточно медленно, чтобы его форма хорошо зафиксировалась в последовательности дискретных образцов. В частности, сигнал не должен иметь синусоидальных составляющих на частотах выше так называемой частоты Найквиста, которая равна половине частоты дискретизации:

Например, если АЦП делает 10 000 измерений в секунду, то входной сигнал не должен превышать частоту 5000 Гц. Что произойдет, если входной сигнал будет меняться быстрее? Эти частотные компоненты нельзя будет реконструировать из образцов, поскольку их происхождение совершенно непонятно (рис. 1).

Рис. 1. Наложение. Синусоидальная волна с частотой 2 кГц (красная) дискретизируется с частотой 10 kS/s (синие точки). Другая синусоида с частотой 8 кГц производит точно такую же последовательность образцов. Таким образом, после дискретизации невозможно понять, исходный сигнал был на 2 кГц или на 8 кГц

Одинаковый набор образцов получается и из сигнала ниже частоты Найквиста, и из любого количества возможных сигналов выше частоты Найквиста. Это явление называется наложением (алиасинг), когда высокочастотный сигнал в дискретизированной форме может маскироваться под низкочастотный сигнал. Если для входящего сигнала не действует никаких ограничений, то наложение приводит к потере информации, потому что мы больше не можем восстановить исходный сигнал из дискретных образцов.

Как избежать наложения? Просто нужно перед дискретизацией устранить из аналогового сигнала частотные составляющие выше частоты Найквиста. Чаще всего это делается электронным фильтром нижних частот, который пропускает нижние частоты, но отсекает высокие. Благодаря повсеместному применению таких фильтров на их совершенствование потрачено немало инженерных усилий. В итоге обычный подход к конструированию системы сбора данных выглядит таким образом (рис. 2):

1. Определите необходимую полосу пропускания сигнала, который нужно зарегистрировать, а именно самую высокую частоту, которую впоследствии нужно восстановить. Это частота Найквиста для вашей системы.

2. Пропустите сигнал через фильтр нижних частот, который отсекает все частоты выше .

3. Запустите дискретизация сигнала после фильтра с частотой .

Рис. 2. Сравнение обычного сбора данных с процедурой, описанной в научной работе Цая и др. Слева: синусоидальная волна на частоте 1 кГц с амплитудой от пика до пика 200 мкВ, как в тестовых записях из научной работы. Добавлен белый гауссовский шум с полосой пропускания 1 МГц и среднеквадратичной амплитудой 21,7 мкВ. Сверху: стандартный подход применения фильтра для защиты от наложения с частотой отсечения 5 кГц, которая исключает бóльшую часть шума и таким образом улучшает соотношение сигнала к шуму (SNR) в 200 раз. Этот сигнал затем дикретизируется на 10 kS/s. Снизу: в научной работе Цая и др. сигнал сразу дискретизируется с сохранением того же низкого SNR. Затем следует цифровая обработка, которая немного увеличивает SNR. Все данные и обработка смоделированы с помощью этого кода

Что утверждают Цай и др.

Теперь рассмотрим конкретную ситуацию из научной работы Дэвида Цая и др. Они хотят записывать электрические сигналы от нейронов, для чего требуется полоса пропускания

Так что они выбрали частоту дискретизации 10 kS/s. К сожалению, требуемый нейронный сигнал искажён из-за широкополосного теплового шума, неизбежного побочного продукта при записи. Спектр шума достигает 1 МГц с типичной среднеквадратичной амплитудой (rms) 21,7 мкВ. Авторы аппроксимируют его как белый гауссовский шум, то есть шум с постоянной плотностью мощности до отсечения на 1 МГц. (Ссылки на эти цифры: стр. 5 и рис. 11 из первой статьи; стр. 2, 5, 9 и рис. 2е в приложении из второй статьи).

Стандартной процедурой стала бы передача сигнала и шума через аналоговый фильтр для защиты от наложения с отсечением частот выше 5 кГц (рис. 2). Это оставит нетронутым нейронный сигнал, в то же время снизив мощность шума в 200 раз, потому что спектр шума срезается с полосы пропускания 1 МГц до всего лишь 5 кГц. Таким образом, оставшийся шум ниже частоты Найквиста будет иметь среднеквадратичную амплитуду всего 21,7 мкВ/ = 1,53 мкВ. Такое количество теплового шума совершенно безобидно. Это меньше, чем от других источников шума в эксперименте. Затем сигнал дискретизируется на частоте дискретизации 10 kS/s.

Вместо этого авторы полностью исключают фильтр и напрямую дискретизируют широкополосный сигнал+шум. В своей статье они подробно объясняют технические ограничения, связанные с нехваткой места на кремниевых устройствах в этом методе записи, из-за которых пришлось отказаться от фильтра. Но в итоге вся мощность шума вплоть до 1 МГц теперь попала в дискретизированный сигнал через наложение. Фактически, каждый образец загрязнён гауссовским шумом со среднеквадратичной амплитудой 21,7 мкВ. Это недопустимый уровень шума, потому что мы хотим различать сигналы нейронов на той же или меньшей амплитуде. Для справки, в некоторых популярных системах для записи мультинейронной активности уровень шума не превышает 4 мкВ.

Здесь Цай с коллегами демонстрируют поразительную «инновацию»: они говорят что можно применить хитрый алгоритм преобразования данных после дискретизации для восстановления оригинального широкополосного шума, вычесть этот шум из дискретизированных данных — и таким образом оставить чистый сигнал. Вот соответствующие цитаты, в дополнение к вышеуказанным: «Мы можем в цифровом виде восстановить спектральный вклад от высокочастотного теплового шума, а затем удалить его из данных с разреженной выборкой, тем самым минимизируя эффекты наложения, без использования фильтров защиты от наложения на каждом канале». И ещё одна: «Мы представляем архитектуры мультиплексирования без фильтров защиты от наложения на каждом канале. Данные разреженной выборки восстанавливаются с помощью стратегии сжатого считывания, включающей в себя статистическую реконструкцию и удаление теплового шума с грубым шагом дискретизации».

Какие доказательства они предъявляют для этого утверждения? Проведён только один эксперимент, который проверяет уменьшение шума с использованием реальных данных. Авторы записали синусоидальный тестовый сигнал на частоте 1 кГц с амплитудой 200 мкВ от пика до пика. Затем применили свою схему обработки для «удаления теплового шума». Выходной сигнал выглядит чище входного (рис. 2e из статьи; см. также симуляцию на рис. 2). Количественно шум сократился со среднеквадратичной амплитуды 21,7 мкВ до 10,02 мкВ. Это довольно скромное улучшение соотношения сигнала к шуму (SNR) в 4,7 раза (подробнее об этом ниже). Правильный фильтр для защиты от наложений перед дискретизацией или заявленная система удаления наложенного шума после дискретизации должны бы увеличить SNR в 200 раз. (Ссылки на процитированные результаты см. на рис. 2e-f из второй статьи и на рис. 7 из первой статьи).

Почему схема Цая и др. не может работать в принципе

Прежде чем перейти к конкретному разбору схемы обработки данных, предложенной в этих научных статьях, стоит подумать, почему она не может работать в принципе. Самое главное: если она работает, то это отменяет теорему Котельникова, которую поколения студентов-инженеров изучали в институтах. Сигнал белого шума в этих экспериментах дискретизируется с частотой в 200 раз ниже той, которая позволяет восстановить этот сигнала по теореме Котельникова. Так почему Цай с коллегами вообще решили, что схема может работать?

Авторы утверждают, что наложенный высокочастотный шум сохраняет некий отпечаток, что позволяет затем удалить его: «Воспользовавшись приведёнными выше характеристиками, мы можем в цифровом виде восстановить спектральный вклад от высокочастотного теплового шума, а затем удалить его из данных с разреженной выборкой, тем самым минимизируя эффекты наложения». Трудно понять, какие это могут быть характеристики. Их проще всего оценить по временнóй шкале. Белый гауссовский шум на полосе 1 МГц можно восстановить по временным рядам независимых образцов из идентичного гауссового распределения с частотой 2 млн образцов в секунду. Теперь возьмите эти временные ряды и сделайте подвыборку на 10 тыс. образцов в секунду, т.е. каждый 200-й из оригинальных образцов. Вы снова получите независимо и одинаково распределённые образцы, т. е. белый гауссовский шум на 10 kS/s. Ничто в этой серии образцов не показывает, что её источником является высокочастотный шум. Он отлично дискретизирован.

Рис. 3. Выборка белого гауссовского шума. Слева: белый гауссовский шум (красная линия) со среднеквадратической амплитудой 21,7 мкВ и полосой пропускания 1 МГц дискретизируется с частотой 10 kS/s (синие точки). Справа: дискретизированный сигнал с расширенной в 200 раз временной шкалой. Это тоже белый гауссовский шум, с тем же распределением амплитуды (поля графика), но полосой пропускания 5 кГц

Авторы также утверждают, что их алгоритм для восстановления белого гауссовского шума «избегает наложения за счёт использования концепций сжатого считывания». Принцип сжатого считывания (compressed sensing) заключается в том, что если сигнал проявляет известные закономерности, то можно дискретизировать его без потерь с частотой меньше, чем частота Найквиста. В частности, такой сигнал проявляет разреженное распределение в пространстве данных по определённым направлениям, что открывает возможности для сжатия. Это относится ко многим естественным источникам сигнала, таким как фотографии. К сожалению, белый гауссовский шум представляет собой абсолютно несжимаемый сигнал без каких-либо закономерностей. Распределение вероятностей для этого сигнала является круглой гауссовой сферой, которая в пространстве данных выглядит одинаково со всех сторон и просто не предусматривает никаких возможностей сжатия. Конечно, нейронные сигналы поверх этого шума содержат некоторые статистические закономерности (подробнее об этом ниже). Но они не помогают восстановить шум.

Как схема Цая и др. терпит неудачу на практике

Я написал код для алгоритма, описанного в научной работе Цая и др. При обработке симуляции авторского теста (синусоидальная волна 200 мкВ с шумом 21,7 мкВ) он выдаёт очищенную синусоидальную волну с шумом всего 10,2 мкВ (рис. 2), что ужасно близко к результату из научной работы 10,02 мкВ. Значит, я правильно эмулировал схему.

По ходу дела я натолкнулся на нечто похожее на серьёзную математическую ошибку. Это относится к убеждению авторов в том, что шум с недостаточным шагом дискретизации сохраняет некую подпись в результате наложения. Ссылаясь на Фурье-представление белого гауссовского шума, они пишут (раздел III.G): «В пространстве Фурье у векторных углов теплового шума (бесконечной длины) равномерное распределение с нулевым средним. Опять же, любое отклонение от этого идеала в сигналах конечной длины усредняется наложением спектров, когда содержимое складывается в первую зону Найквиста (в результате чего углы сходятся к нулю)». И аналогично «спектральные углы сходятся к нулю в варианте наложения теплового шума» (стр. 9 слева внизу). Это неверно. Фазовые углы описываемых здесь векторов Фурье имеют равномерное круговое распределение; у этого распределения нет среднего угла. После усреднения из-за нормализации некоторых из этих векторов фаза среднего вектора снова приобретает равномерное круговое распределение. Это подтверждается в пространстве Фурье, что проще оценить в непосредственном пространстве: подвыборка из белого гауссовского шума снова выдаёт вам белый гауссовский шум (рис. 3). Обоснование алгоритма Цая основано на этой ошибочной концепции, что фазовые углы каким-то образом усредняются до нуля.

Итак, каким же образом алгоритм Цая очищает синусоидальный тестовый сигнал? Это не так уж сложно. Если вы знаете, что сигнал — чистая синусоида, то остаётся лишь три неизвестных: амплитуда, фаза и частота. Очевидно, вы можете извлечь эти три неизвестных из 10 000 образцов шума, которые получаете каждую секунду. Можно сделать и гораздо эффективнее: найти наибольшую Фурье-составляющую в сэмплированной записи и обнулить все остальные. Это почти полностью устраняет шум (подробнее см. здесь). Алгоритм Цая примерно так и делает: сильнее подавляет внепиковые частоты в преобразовании Фурье, чем пиковые — и получает некую сумму синусоиды и подавленного шума (см. также рис. 9 в работе). Как мы увидим дальше, заявленная производительность не распространяется на реалистичные сигналы.

Что стало бы разумной схемой обработки?

5 кГц, но спектр не плоский во всём диапазоне (рис. 4).

Рис. 4. Слева: усреднённые биоэлектрические потенциалы для 15 ганглиозных клеток сетчатки мыши [источник]. Справа: их энергетический спектр

Предположим, мы знаем энергетический спектр сигнала, и он отличается от спектра шума — как тогда обрабатывать данные выборки, чтобы оптимально восстановить сигнал? Это классическая задача, которую задают на курсе обработки сигналов. Оптимальный линейный фильтр для реконструкции c минимизацией средней квадратической ошибки называется фильтром Винера. По сути, он подавляет частотные компоненты, где шум относительно больше. Но алгоритм Цая — нелинейная операция (см. подробности здесь), так что теоретически он может превзойти фильтр Винера. Кроме того, из-за нелинейности невозможно предсказать эффективность алгоритма на более обычных сигналах по его производительности на синусоидальных сигналах (см. выше). Поэтому я сравнил алгоритм Цая с классическим фильтром Винера, используя различные предположения для спектра. В частности, сигнал был ограничен ниже частоты среза в диапазоне от 100 Гц до 5000 Гц, в то время как шум имел равномерный спектр в полосе 5 кГц:

Рис. 5. Энергетический спектр сигнала (цветные линии) и шума (чёрная), используемые в расчётах на рис. 6. Шум гауссов и белый во всём диапазоне. Сигнал получен из гауссовского белого процесса, пропущенного через однополюсный фильтр нижних частот с частотами отсечки при 5000, 2000, 1000, 500, 200, 100 Гц.

Для каждого из этих сочетаний сигнала и шума я применил фильтр Винера и алгоритм Цая — и измерил соотношение сигнала к шуму (SNR) в результате (рис. 6).

Рис. 6. Как алгоритм Цая и фильтр Винера изменяют SNR. Каждая панель соответствует различному энергетическому спектру сигнала (см. рис. 5). Сигнал и шум на разных SNR отложены по горизонтальной оси. Смешанный сигнал и шум пропустили через фильтр Винера или алгоритм Цая, а SNR выходного сигнала отложен по вертикальной оси. Красный — фильтр Винера; зеленый — алгоритм Цая; пунктир — подлинник.

Как и ожидалось, фильтр Винера всегда улучшает SNR (сравните красную кривую с точечным подлинником), и тем больше, чем сильнее отличие спектров сигнала и шума (панели от левой верхней к нижней правой). Во всех вариантах фильтр Винера превосходит алгоритм Цая в улучшении SNR (сравните красные и зелёные кривые). Кроме того, во многих случаях алгоритм Цая фактически ухудшает SNR (сравните зелёные и пунктирные кривые). Учитывая, что алгоритм основан на математических ошибках, это неудивительно.

Есть и более сложные схемы подавления шума, чем фильтр Винера. Например, мы знаем, что интересующие записи нейронной активности представляют собой наложение импульсоподобных событий — биоэлектрических потенциалов — чьи формы всплесков описываются всего несколькими параметрами. В рамках этой статистической модели можно разработать алгоритмы, которые определят среди шума оптимальные пиковые значения каждого из событий. Это активная область научных исследований.

Почему это важно для нейронауки

Исследователи из разных нейронаук активно стремятся увеличить число одновременно отслеживаемых нейронов. В этой области экспоненциальный прогресс, хотя довольно медленный, с удвоением каждые семь лет. Несколько проектов направлены на ускорение этого процесса путём создания крупномасштабных КМОП-микросхем с массивом из тысяч плотно расположенных электродов и мультиплексеров [в том числе работа Цая — примеч. пер.]. Это дорогие исследования. Чтобы довести электродные решётки до стадии прототипа, требуются миллионные вложения. Если успех подобного прибора основан на ошибочных представлениях о наложении и неоправданных ожиданиях от программного обеспечения, это может привести к дорогостоящим провалам и растрате ценных ресурсов.

Болезненным провалом такого рода стал массив Фромхерца. Сконструированный в сотрудничестве с Siemens за миллионы дойчмарок, он стал самым большим массивом биоэлектродов для своего времени, с 16 384 датчиками на площадке 7,8×7,8 мкм. Для экономии места и по другим причинам разработчики отказались от использования фильтров защиты от наложения. Наложение и прочие артефакты в итоге привели к уровню шума 250 мкВ, непригодному для каких-либо интересных экспериментов, так что инновационное устройство так никогда и не использовали в деле. А ведь такой исход можно было предсказать простым расчётом.

Если рационально предусматривать последствия наложения, то возможны полезные компромиссы. Например, в недавно созданном устройстве с кремниевыми штырьками тоже отсутствуют фильтры защиты от наложения в мультиплексерах. Но коэффициент субдискретизации всего 8:1, в результате чего избыточный шум не превышает критических значений. В сочетании с правильным восстановлением сигнала такая схема вполне жизнеспособна.

Кто проверял эту работу?

Как всегда, встаёт вопрос: эти драматические заявления Цая и др. прошли рецензирование? Неужели никого не удивило очевидное противоречие теореме отсчётов? Кто вообще рассматривал эти материалы? Ну, я их рассмотрел. Для другого журнала, где статью в итоге отклонили. До этого была длительная переписка с авторами, в том числе я дал им задачу удалить шум наложения из смоделированной записи (задача ниже, только без денежной награды). Авторы посчитали вызов обоснованной проверкой алгоритма, но полностью провалили тест. Каким-то образом это не поколебало их уверенности — и они представили точно такую же научную статью двум другим журналам. Эти журналы, видимо, после так называемого рецензирования, с радостью согласились на печать.

Ещё несколько правил: предложение действует в течение 30 дней со дня публикации [20 марта 2018 года — примеч. пер.]. Выигрывает только первая квалификационная запись. Вы должны раскрыть используемый алгоритм, чтобы я мог воспроизвести его работу. После сражения с теоремой отсчётов вас может заинтересовать какая-нибудь другая задача, например, криптографическая атака на случайный seed, который я использовал для создания файла данных. Хотя мне было бы интересно узнать о таких альтернативных решениях, но я не буду платить за это 1000 долларов, а только верну ваши 10 долларов.

Итоги

Пока никто не получил 1000 долларов, выводы следующие:

Источник