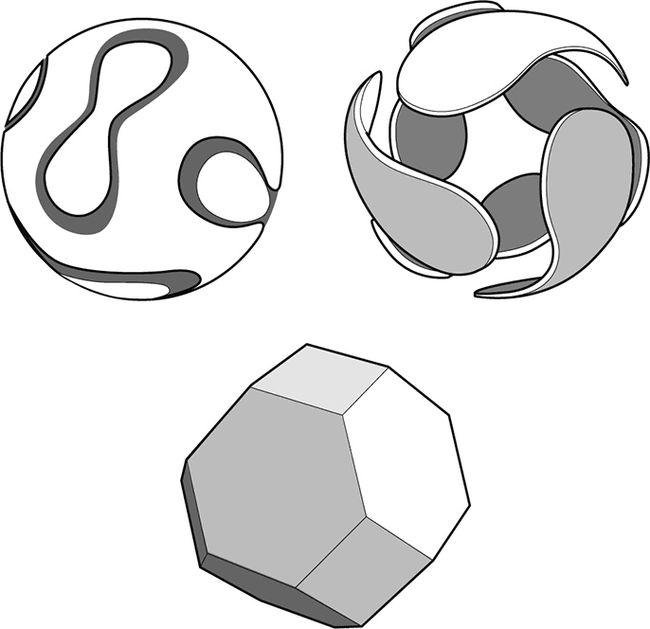
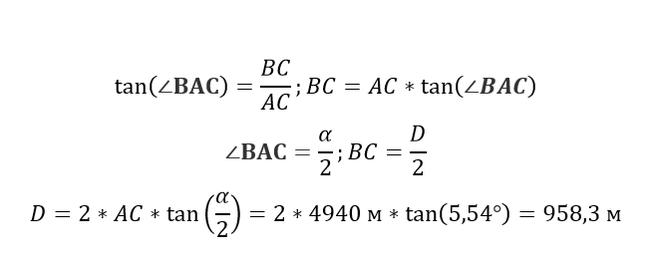геометрическая форма футбольного мяча

Геометрическая форма футбольного мяча

Поверхность классического футбольного мяча состоит из слегка искривлённых 12 правильных пятиугольников чёрного цвета и 20 правильных белых шестиугольников. Модель мяча можно представить следующим образом.

Из 12 правильных пятиугольников и 20 правильных шестиугольников с равными сторонами можно сложить многогранник, называемый усечённым икосаэдром.

«Отрежем» (отсечём) вершины икосаэдра, отступив от вершин вдоль прямых, направленных в центр, на столько, чтобы оставшиеся части граней были правильными шестиугольниками. Срезы будут правильными пятиугольниками. Получившаяся фигура и есть усечённый икосаэдр.

Усечённый икосаэдр — один из полуправильных многогранников. Так называются многогранники, у которых все грани — правильные многоугольники нескольких разных типов (в отличие от правильных многогранников, все грани которых — одинаковые правильные многоугольники), а все вершины устроены «одинаково», т. е. многогранные углы при вершинах равны (совместимы).

При «наполнении воздухом» модели (усечённого икосаэдра) она принимает форму сферы, становится футбольным мячом. При этом вершины усечённого икосаэдра совпадут с «вершинами» мяча, рёбра перейдут в швы, а грани — в слегка искривлённые много­угольники на поверхности мяча. Таким образом получится мяч — центральная проекция усечённого икосаэдра на сферу.

Раздувание усечённого икосаэдра заставляет задуматься о степени близости к шару формы изначальной модели. Например, можно оценивать это сходство отношением радиусов концентрических сфер — описанной (проходящей через вершины; будущий мяч) и вписанной. Чем ближе это отношение к единице, тем совершеннее модель, тем ближе она к идеально круглому мячу.

А нельзя ли придумать модель мяча, состоящую из плоских кусков (панелей), но более совершенную, чем классическая? Можно было бы взять не усечённый икосаэдр, а многогранник с большим числом вершин, но это не устраняет принципиальный недостаток — выступающие над вписанной сферой «пирамидки» (вершины), мешающие модели стать сферой. К тому же процесс изготовления существенно усложняется.

Классический пятнистый мяч появился только в 1950 году. Он был официальным мячом на чемпионатах мира с 1970 до 2002 года. Затем наступило время экспериментов, а в 2014 году на чемпионате мира в Бразилии состоялась премьера нового официального мяча, получившего название «Бразука».

Модель «Бразуки» совершеннее классической и при этом «является кубом»! Как и куб, она собирается из шести одинаковых плоских панелей, на ней выделяются восемь особых точек (вершин), в каждой из которых сходится по три панели.

Панели можно склеивать по линиям границ между углами, поскольку длины этих линий одинаковы. Выпуклые участки границ склеиваются с вогнутыми, а линии подобраны так, что в каждой точке склейки кривизна выпуклого участка больше кривизны вогнутого. Из‐за этого плоские панели при склеивании изгибаются, образуя в результате замкнутую выпуклую поверхность. Возможность такой склейки гарантирует теорема А. Д. Александрова, академика и автора школьного учебника по геометрии.

В модели классического мяча вся кривизна сосредоточена в конечном числе «выступающих» вершин. А в модели «Бразуки» она распределена более равномерно (по длинным рёбрам), и из‐за этого модель становится более близкой к сфере.

Источник

Футбольный мяч и фуллерены

Число называется эйлеровой характеристикой многогранника. Легко вычислить эйлерову характеристику для некоторых знакомых нам многогранников.

Многогранник
Тетраэдр	4	6	4	2
Куб	8	12	6	2
Октаэдр	6	12	8	2

Доказательство теоремы Эйлера может быть найдено здесь.

Давайте воспользуемся теоремой Эйлера для установления некоторых интересных фактов. Посмотрите на изображение футбольного мяча.

Вопрос: сколько нужно взять пятиугольников, чтобы сшить мяч? Пусть – количество шестиугольников, а – количество пятиугольников. Давайте применим теорему Эйлера к нашему футбольному мячу:

где , , а . Формулы для количества вершин, ребер и граней легко получаются из наблюдения, что каждая вершина попадает на три грани, а по каждому ребру пересекаются только две грани. Подставив значения в формулу, вы получите ответ: . Переменная исключается из уравнения, т.е. количество шестиугольников может быть каким угодно. На следующей картинке изображен мяч, сшитый из одних только пятиугольников. Сколько их?

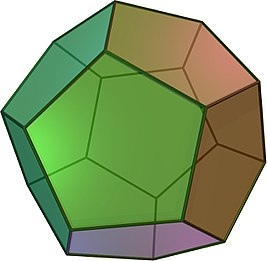
Этот многогранник называется додекаэдром и является одним из пяти правильных многогранников.

Давайте рассмотрим другой сюжет. Фуллерены — молекулярные соединения, принадлежащие классу аллотропных форм углерода и представляющие собой выпуклые замкнутые многогранники, составленные из чётного числа трёхкоординированных атомов углерода. Своим названием фуллерены обязаны инженеру и архитектору Ричарду Бакминстеру Фуллеру, чьи геодезические конструкции построены по этому принципу. Первоначально данный класс соединений был ограничен лишь структурами, включающими только пятиугольные и шестиугольные грани.

И наконец, давайте посмотрим на следующую картинку.

Ничего особенного — всего лишь купол, собранный из шестиугольников. А теперь еще раз помедитируйте над формулой Эйлера и вперед искать пятиугольники.

Этот и многие другие математические сюжеты смотрите в замечательных лекциях Алексея Савватеева или в его книге «Математика для гуманитариев».

Источник

Круглый значит кубический

Официальный мяч XXI чемпионата мира по футболу

Marcelo Machado De Melo/Global Look Press

В честь начинающегося сегодня XXI чемпионата мира, который пройдет с 14 июня по 15 июля, сайт «Математические этюды» рассказал о геометрии разных футбольных мячей, а также о том, почему официальный мяч чемпионата — это куб, как сделать модель мяча при помощи зеркал и скотча и при чем тут телевизионный спутник. С разрешения редакции Indicator.Ru публикует материал у себя.

Классика

Поверхность классического футбольного мяча состоит из «слегка искривленных» 12 правильных пятиугольников черного цвета и 20 правильных белых шестиугольников и представляет собой многогранник, называемый усеченным икосаэдром.

Икосаэдр — один из пяти правильных многогранников. Его название происходит от древнегреческих слов εἴκοσι — «двадцать» и ἕδρον — «основание». У икосаэдра 12 вершин, 20 граней (правильных треугольников), 30 ребер.

«Отрежем» вершины икосаэдра, отступив от вершин вдоль прямых, направленных в центр, на столько, чтобы оставшиеся части граней были правильными шестиугольниками. Очевидно, что срезы будут правильными пятиугольниками. Получившаяся фигура и есть усеченный икосаэдр.

Усеченный икосаэдр — один из полуправильных многогранников. Так называются многогранники, у которых все грани — правильные многоугольники нескольких разных типов (в отличие от правильных многогранников, все грани которых — одинаковые правильные многоугольники), а все вершины устроены «одинаково», то есть многогранные углы при вершинах равны (совместимы).

Источник

Математика футбольных мячей

Задача

Почти 50 лет назад, к чемпионату Европы по футболу 1968 года, компания Adidas разработала новый футбольный мяч Telstar. Он получился настолько удачным, что его вид и покрой можно считать классическими: это 20 шестиугольников и 12 пятиугольников, сшитых или склеенных по сторонам (далее будем называть стороны многоугольников ребрами) так, что в каждой вершине сходится по три ребра. Поверхность такого футбольного мяча очень близка к поверхности шара (сфере).

Теперь представим, что есть много шестиугольников и пятиугольников, из которых удалось склеить похожий на сферу многогранник по тем же принципам: приклеивая ребра к ребрам, чтобы в каждой вершине сходились ровно три ребра. Оказывается, сколько бы ни было использовано шестиугольников, в нем будет ровно 12 пятиугольников. Докажите это!

Подсказка 1

Вам поможет знаменитая формула Эйлера: если на плоскости или на сфере нарисован граф с v вершинами, r ребрами и γ гранями, то выполнено равенство v − r + γ = 2. Гранью графа называется часть плоскости, ограниченная ребрами, растягивая, но не разрывая которые можно сделать круг.

Подсказка 2

Для начала, конечно, нужно понять, как футбольный мяч связан с графом. Действительно, давайте считать, что пятиугольники и шестиугольники — это грани графа, их стороны — ребра графа, а вершины — вершины графа. Тогда мы получаем граф, нарисованный на поверхности сферы. Предположим, что мы взяли n шестиугольников и m пятиугольников. Остается понять, какие ограничения на число m ставит формула Эйлера.

Решение

Итак, допустим, что мы взяли n шестиугольников и m пятиугольников. Посчитаем, сколько будет вершин, ребер и граней в соответствующем графе. Каждый из n шестиугольников дает по шесть вершин, а каждый из m пятиугольников — по пять, значит всего будет 6n + 5m вершин. Однако заметим, что каждую из этих вершин мы посчитали трижды, потому что склеивали по три многоугольника в каждой вершине. Итого в графе v = (6n + 5m)/3 вершин. Аналогично получаем, что r = (6n + 5m)/2. Очевидно, что количество граней просто равно количеству многоугольников: γ = m + n.

Теперь запишем формулу Эйлера:

То есть, действительно, если пытаться склеить сферический многогранник так, как описано в условии, то при любом числе шестиугольников потребуется ровно 12 пятиугольников. И это абсолютно строгое доказательство — никакой магии.

Послесловие

Будем далее называть фуллеренами выпуклые многогранники, которые удовлетворяют свойствам из условия: в каждой вершине сходится по три ребра, а гранями являются только пятиугольники и шестиугольники (не обязательно правильные). Вообще, фуллерены — это одна из аллотропных форм углерода: сферические молекулы из атомов углерода, каждый атом в которых принадлежит ровно трем углеродным кольцам, состоящим из 5 или 6 атомов. То есть такое название наших многогранников вполне оправданно.

Первый из открытых фуллеренов, С₆₀, содержал 60 атомов углерода. Он был синтезирован Р. Кёрлом, Г. Крото и Р. Смолли в 1985 году, причем нельзя сказать, что они сделали это целенаправленно: химики облучали твердые графитовые образцы лазером и анализировали состав конденсированных паров графита, в которых при помощи масс-спектрометрии и были обнаружены кластеры из 60 и 70 атомов углерода. Позже удалось подтвердить, что это действительно С₆₀ (и другой фуллерен — С₇₀, состоящий из 70 атомов). За это в 1996 году им была присуждена Нобелевская премия по химии.

В свою очередь, фуллеренами эти молекулы были названы в честь американского архитектора, дизайнера и изобретателя Ричарда Бакминстера Фуллера, который запатентовал конструкцию куполов для покрытия больших площадей с опорами только на границе (см. послесловие к задаче «Карандаши и нитки»).

Фуллерены встречаются в природе, попадаются в космосе, имеют многочисленные приложения в биологии, медицине и нанотехнологиях и неоднократно становились героями новостей на нашем сайте (см. подборку материалов ниже).

У многогранника, имеющего форму футбольного мяча и с которого началась эта задача, тоже 60 вершин (это нетрудно проверить, зная формулу Эйлера!) и по форме он почти неотличим от фуллерена С₆₀. Разница в том, что у фуллерена разные «ребра» — длины связей между атомами углерода: общая сторона двух шестиугольников имеет длину 1,39 Å, а общая сторона шести- и пятиугольника длиннее и равна 1,44 Å. Посмотрим на этот многогранник повнимательнее с математической точки зрения.

Начнем с икосаэдра — правильного многогранника, состоящего из 20 треугольных граней, сходящихся по пять в каждой из 12 вершин. Представим, что он сделан из сыра и отрежем острым ножом каждую вершину. Полученный многогранник логично называть усеченным икосаэдром. Нетрудно заметить, что треугольные грани превратились в шестиугольные, а на месте каждой вершины появилась пятиугольная грань (рис. 1). Таким образом, если считать, что мы резали идеально ровно и все шестиугольные и пятиугольные грани получились одинаковыми, то мы получили правильный усеченный икосаэдр — это и есть «футбольный мяч» (только из сыра).

Рис. 1. Правильный икосаэдр и усеченный икосаэдр. Рисунки с сайта ru.wikipedia.org

Как и правильный икосаэдр, так и полученный из него усеченный икосаэдр имеет икосаэдрическую группу симметрии: существует 120 разных движений трехмерного пространства (в данном случае это повороты и отражения), которые переводят в себя правильный усеченный икосаэдр. Фуллерены с такой группой симметрии называются многогранниками Гольдберга (см. Goldberg polyhedron). В силу своей симметричности они состоят из правильных пяти- и шестиугольников. Интересно, что среди фуллеренов-молекул есть и такие, у которых вообще нет симметрий (H. Yang et al., 2011. Fullerenes without symmetry: crystallographic characterization of C₁(30)–C₉₀ and C₁(32)–C₉₀).

Как мы доказали в задаче, в многограннике Гольдберга всегда 12 пятиугольников, поэтому можно задавать его расположением пятиугольников. А именно, будем ходить от одного пятиугольника до другого «ходом коня»: сначала на m шагов в одном направлении, затем поворот на 60° и еще n шагов. Оказывается, полученный такой странной процедурой многогранник GP(m, n) будет обладать икосаэдрической группой симметрии. Самый простой пример многогранника Гольдберга, GP(1, 0) — это додекаэдр (правильный многогранник, состоящий из 12 пятиугольников). На рис. 2 показаны многогранники Гольдберга для двух других значений параметров m и n: GP(1, 4), GP(7, 0). Кстати, количество шестиугольников в многограннике Гольдберга выражается через m и n: оно равно 10(m 2 + mn + n 2 − 1) (попробуйте это доказать!).

Рис. 2. Многогранники Гольдберга GP(1, 4), GP(7, 0). Рисунки с сайта en.wikipedia.org

Встречаются фуллерены и с иными группами симметрий. Здесь нужно отметить, что математики любят исследовать объекты, обладающие симметриями: отчасти из-за того, что это обычно бывает проще и удобнее, а отчасти из-за того, что такие объекты нередки в природе и их удобно использовать при моделировании реальных процессов.

Упомянем и о другой связи додекаэдра с фуллеренами. Математики В. Бухштабер и Н. Ероховец в 2015 году показали, что каждый фуллерен комбинаторно эквивалентен (то есть мы разрешаем изменять длины ребер и величины углов, но не разрешаем изменять количества пятиугольников и шестиугольников, — и смотрим, какие многогранники можно такими преобразованиями получить друг из друга) многограннику, получаемому из додекаэдра при помощи последовательности специальных «усечений». Например, один из типов усечений выглядит так: нужно взять пару точек на сторонах существующей грани, соединить их отрезком и «сломать» эти стороны в выбранных точках (в указанной статье эта операция показана на рис. 6). В этой же статье показано, что не существует фуллеренов с одним шестиугольником, но зато существуют фуллерены с любым другим числов шестиугольников! Например, если шестиугольников нет совсем, то это додекаэдр. Попробуйте понять, как устроен фуллерен, содержащий ровно два шестиугольника (ответ можно найти всё в той же статье на рис. 20).

Источник

Геометрия футбольного мяча

Вчера победой Франции завершился чемпионат мира по футболу! А знаете ли вы, какой на самом деле формы футбольный мяч?

«Мяч должен быть сферическим» гласят правила игры в футбол от FIFA. Очевидная мысль, но так ли это просто сделать? Если присмотреться к мячу, можно увидеть, что он покрыт различными геометрическими фигурами. Образуют ли они сферу?

Природа хороша в изготовлении сфер, но людям это удаётся не так просто. Например, для игры в настольный теннис нужны идеально круглые мячи. Их изготавливают склеиванием двух полусфер, но так количество брака достигает 95%. Отбраковка некачественных мячей выглядит весело: специальная пушка запускает мячи в воздух. Круглые летят по прямой, а мячи неидеальной формы отклоняются вбок. Потому что физику не обманешь 🙂

Футбольные мячи сплавлением частей изготовить не получится. Они переносят очень сильные удары и должны быть обшиты прочным материалом. Раньше использовалась кожа, сейчас — синтетика. Части для обшивки всегда вырезают из плоских листов. Какой же формы их вырезать так, чтобы было возможно обшить ими сферу?

Древнегреческий философ Платон предложил пять «идеальных форм», состоящих из одинаковых геометрических фигур

1. Меньше всего компонентов — 4, требуется для пирамиды с треугольным основанием — тетраэдра. Но такой футбольный мяч будет не очень хорошим: у него слишком мало граней. Подойдёт разве что для игры в футболь

2. Из 6 квадратов можно составить куб. Кажется, что это тоже не очень хороший вариант, но он послужил основой первым футбольным мячам. Мяч для самого первого чемпионата мира 1930 года состоял из 12 прямоугольных полосок кожи, сгруппированных в шесть пар и расположенных таким же образом, как при сборке куба. Второй мяч чемпионата состоит из 6 кусков, вырезанных в форме буквы «H» и также основан на кубе

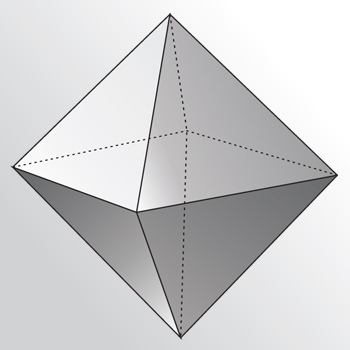
3. Восемь равносторонних треугольников могут быть составлены симметрично, образуя октаэдр. Это два тетраэдра, соединённые основаниями. При правильном соединении невозможно сказать, где был стык

4. Додекаэдр состоит из 12 пятиугольных граней. Видно, что чем больше граней, тем более круглым становится мяч

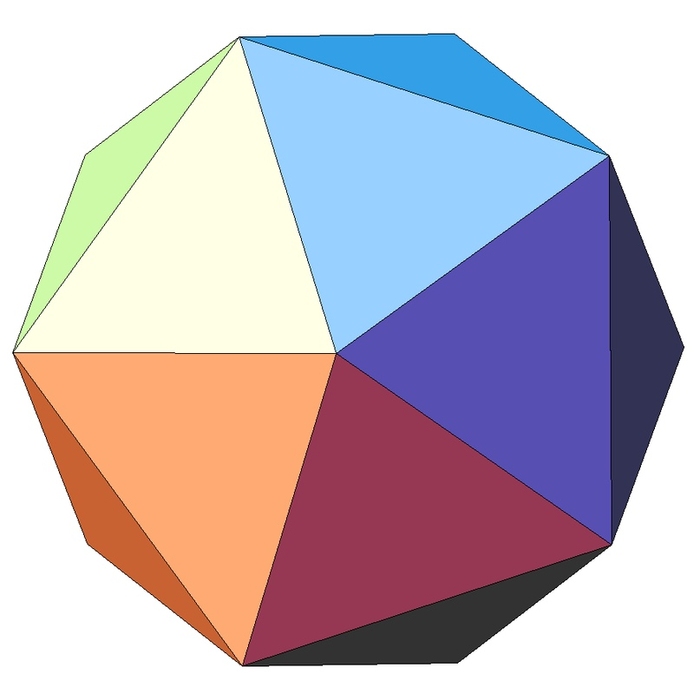
5. Лучшим приближением к сфере является последнее Платоново тело — икосаэдр, состоящий из 20 правильных треугольников. Более сферической формы из одной геометрической фигуры не составить

Другой древнегреческий учёный, Архимед решил улучшить Платоновы тела. Он не ограничивал себя одной плоской геометрической фигурой, а пытался достичь как можно более сферической формы, используя несколько

Его первой идеей было «срезать» углы у фигур Платона. Так, если отсечь углы у тетраэдра, треугольные грани превратятся в шестиугольные, а на месте разрезов появятся новые треугольники. Такая фигура называется усечённым тетраэдром и который выглядит уже более круглым, чем пирамида

Также Архимед поступил и с другими Платоновыми телами, получив из них 7 новых фигур. Кроме того, геометр дополнил их 6 фигурами собственного изобретения. Все вместе они стали называться Архимедовыми телами

Именно одно из 13 Архимедовых тел послужило основой новому футбольному мячу Teamgeist, представленному на чемпионате мира 2006 года в Германии. Этот мяч, слывущий самым круглым, состоит из 14 фигурных кусков, но структурно он соответствует усеченному октаэдру. Возьмите октаэдр, состоящий из восьми равносторонних треугольников, и обрежьте шесть его вершин. Восемь треугольников становятся шестиугольниками, а на месте шести вершин появляются квадраты

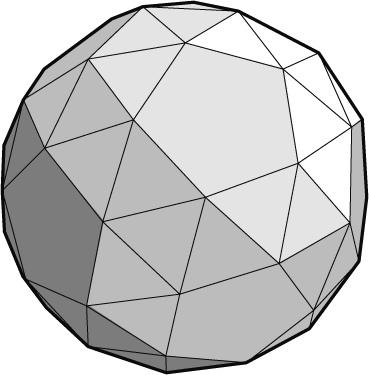
Возможно, будущие чемпионаты мира отличатся более экзотическими Архимедовыми футбольными мячами. Например, плосконосым додекаэдром, состоящим из 92 симметричных компонентов: 12 правильных пятиугольников и 80 равносторонних треугольников

Так даже за развлечениями скрывается интереснейшая наука!

Больше постов о науке, учёбе и IT можно найти в моей группе. Материал поста основан на книге Маркуса дю Сотоя «Тайны чисел»

Лига образования

1.9K пост 16.5K подписчика

Правила сообщества

Публиковать могут пользователи с любым рейтингом. Однако мы хотим, чтобы соблюдались следующие условия:

-уважение к читателю и открытость

-публикация недостоверной информации

-конструктивные дискуссии на тему постов

-личные оскорбления и провокации

-неподкрепленные фактами утверждения

Это два тетраэдра, соединённые основаниями.

Простите, что? Возможно, вы имели в виду «две правильные четырёхугольные пирамиды?»

На 12 лет текст устарел )))

Мне одному померещилось, что мяч нам не рад?

если делают мяч из синтетики, в чем проблема сделать полностью цельный круглый мячик?))

— «А знаете ли вы, какой на самом деле формы футбольный мяч?»

— Нет, не знаем, может быть квадратный?

Вратарь женской сборной Ирана по футболу оказался мужиком?

https://news.sportbox.ru/Vidy_sporta/Futbol/national_teams/s.
Президент Футбольной ассоциации Иордании Али бен аль-Хусейн выступил с обращением к Азиатской футбольной конфедерации (AFC) с просьбой провести проверку в отношении вратаря женской сборной Ирана.

Бен аль-Хусейн усомнился, что голкипер является женщиной. Ранее Иран одержал победу над Иорданией в серии пенальти (4:2) и отобрался на Кубок Азии 2022.

— Просим AFC инициировать четкое расследование, которое проведет медицинский эксперт. Они должны выяснить, является ли женщиной данный игрок, учитывая, что женская сборная Ирана имеет богатую историю в этом отношении, проявляя манипуляцию с полом, — сообщается в заявлении аль-Хусейна.

Ранее стало известно, что четыре игрока женской сборной Ирана были мужчинами.

Молдавские учёные решили проблему, над которой 140 лет бились математики всего мира

Два математика из Молдовы первыми в мире решили алгебраическую проблему, над которой 140 лет размышляли великие ученые мира. Об этом на этой неделе сообщил Технический университет Молдовы (UTM).

«Доктор физико-математических наук Михаил Попа и доктор математических наук Виктор Прикоп первыми в мире нашли решение знаменитой проблемы центра и фокуса, поставленной выдающимся французским математиком Анри Пуанкаре, над которой великие математики мира размышляли более века», — говорится на сайте университета.

Этой проблеме посвятили тысячи работ математики из Франции, России, Беларуссии, Китая, Великобритании, Канады, США и других стран мира. Только в Молдове число работ, посвященных проблеме Пуанкаре, приближается к сотне, отметили в UTM.

Профессор университета Михаил Попа, основатель научной школы алгебры Ли и дифференциальных систем, предложил собственное решение проблемы центра и фокуса, которое привело его к результату, ставшему открытием.

Во время исследований к профессору присоединился его ученик Виктор Прикоп. Вместе они усовершенствовали первоначальную гипотезу в монографии «Проблема центра и фокуса. Алгебраические решения и гипотезы».

Работа была переведена на английский язык и представлена для издания в несколько зарубежных издательств. В итоге лучшие условия предложил издательский дом «Taylor & Francis Group», расположенный в Великобритании и специализирующийся на публикациях научной литературы и журналов.

Где-то всплакнул Гриша Перельман.

Панорама, да не та. И с такими лицами не шутят.

И вот кто он, после этого?

Ведущая из Бразилии устраивает мастер-класс

Что такое наука и какие задачи она должна решать? Существует ли музыкальная наука и какими могут быть результаты применения научного метода в этой сфере? Что такое микрохроматика и как она может изменить музыку будущего, расширить возможности её создания и восприятия?

Как древние греки вычислили длину окружности Земли

Коротко и наглядно о том, как древнегреческий математик и астроном Эратосфен Киренский вычислил размеры Земли ещё в III веке до нашей эры.

Реставрирую шкаф

Работа не быстрая, поэтому фото до. Нашел в нем тайник, в тайнике фото.
Интересует, что за формула на доске?
Пока ответа не нашлось.
Шкаф в СПБ. Ещё была найдена карта Казани печать старая начало 20 века.

Интерактивная футбольная стена

Школьники не смогли решить заданную Мишустиным задачу

1 сентября 2021, 13:04Текст: Алексей Дегтярев
Премьер-министр Михаил Мишустин в ходе визита в физтех-лицей имени Капицы на День знаний на уроке одиннадцатиклассников задал им физтеховскую задачу.
Глава правительства вошел в класс с букетом цветов, он вручил их преподавателю математики Ольге Браславской, ученики в этот момент решали задачу по анализу бизнес-проектов, передает РИА «Новости».
«Зачем же в физтехе бизнес-проектами заниматься, ребята? Здесь нужны фундаментальные знания, правильно?», – обратился к учащимся премьер.
«В современное время нужны специалисты на все руки, особенно в России», – ответили ученики.
Мишустин на доске начертил задачу для школьников, он предложил провести перпендикуляр от точки окружности к диаметру, не используя никаких измерительных приборов, и дал время на ее решение, сообщив, что зайдет позднее.
Школьники начали бурно обсуждать задачку и искать ответ, но не смогли справиться с ней.
Мишустин вернулся в класс и раскрыл решение задачи, подкрепив его ответом на доске.
«Конечно, очень важно решать задачи, связанные с бизнесом, и с приложением математических фундаментальных знаний, которыми вы обладаете. Но мне кажется, в вашем возрасте хорошо бы фундаменталки поднабраться. А когда вы будете обладать математическими знаниями, физикой, химией, вы сможете решать любые задачи, включая бизнес», – сказал премьер.
Напомним, Мишустин в День знаний посетил физтех-лицей имени Капицы, который находится в подмосковном Долгопрудном. Обучение в вузе ведется с 5 по 12 классы. С 2015 по 2021 годы лицей выпустил 94 медалиста, 85 победителей и призеров заключительного этапа Всероссийской олимпиады школьников, 45 победителей и призеров международных олимпиад.

Есть хет-трик

Российская команда по пляжному футболу выиграла третий раз в Чемпионате мира!

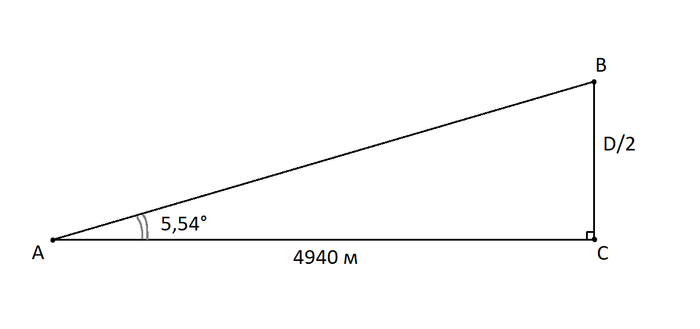
Каких размеров Селестия и как далеко она находится | Genshin Impact

Еще можно измерить угловой размер Селестии, но об это позже
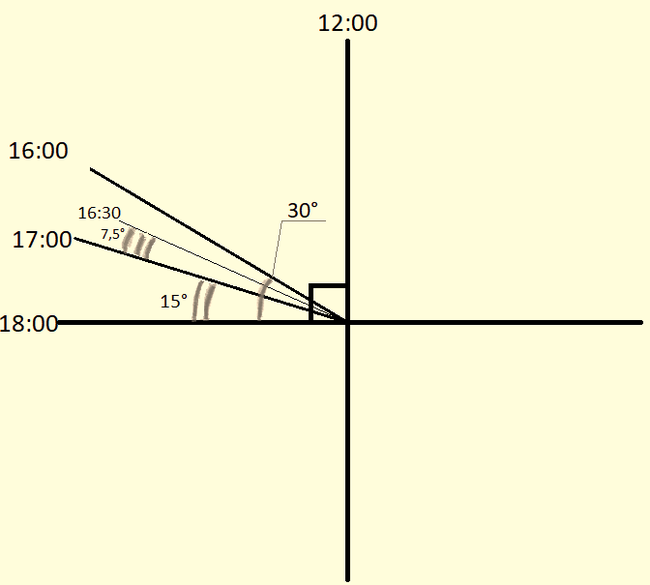
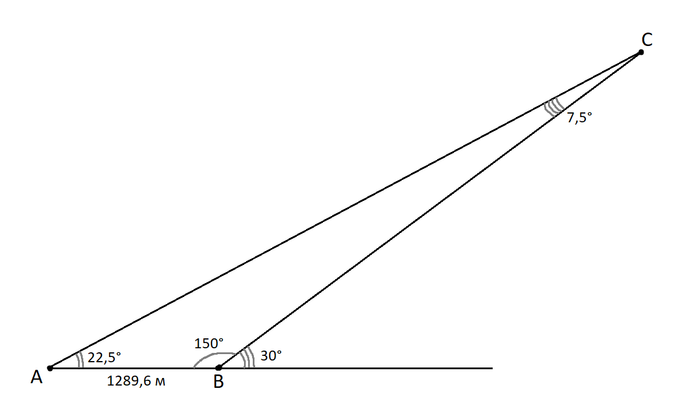
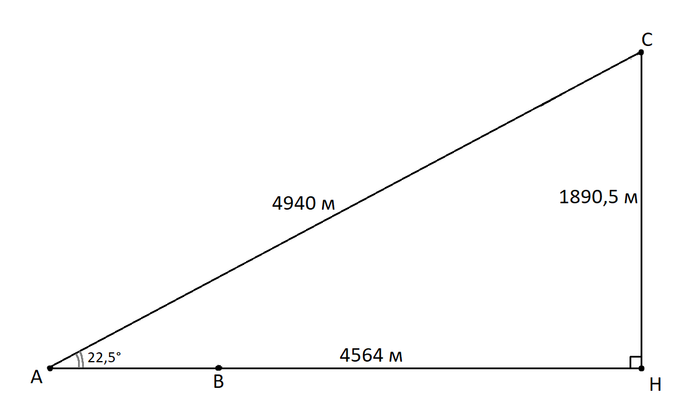
И так, у нас есть необходимые данные: расстояние между точками замера 1289,6 м, угол над горизонтом в Монштадте

22,5°, возле логова Ужаса Бури

Ох уж этот неформальный математический стиль

Что, если наш 4D мир станет пятимерным?

Краткая текстовая версия видео:

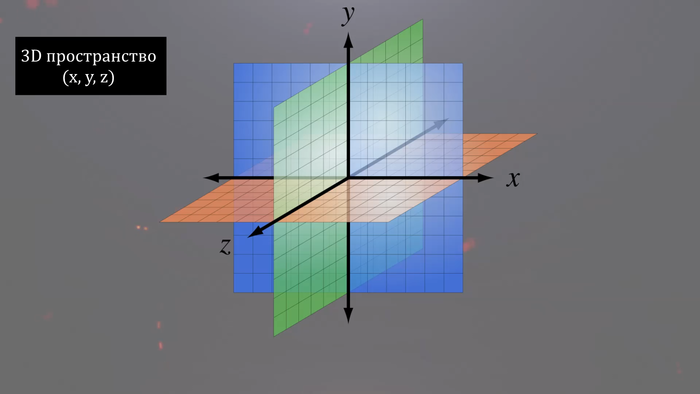
Мир, в котором мы живем, является четырехмерным. По крайней мере в макро масштабе. В нашем мире 3 пространственных измерения и одно временное. Трехмерность пространства значит, например, то, что мы можем в нем провести три взаимно перпендикулярных координатных осей расположенных под углом 90 градусов. В таком пространстве можно двигаться «влево-вправо», «вперед-назад» и «вверх-вниз».

В трехмерном пространстве мы можем завязать узел. В двумерном пространстве завязать узел невозможно. А еще в трехмерном пространстве стул может стоять только на трех ножках или больше, стул на двух ножках потеряет равновесие и упадет (Речь идет о ножках типа такого, как на фото).

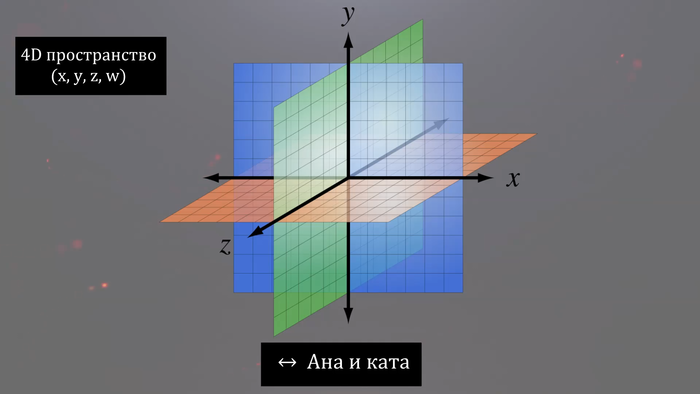
А что будет, если мы добавим еще одно пространственное измерение? То есть представим себе пятимерный мир, 4 пространственных измерения и 1 временное?

В таком мире можно провести еще одну ось перпендикулярную к остальным трем осям под углом 90 градусов. В трехмерном пространстве сделать это невозможно и как-то точно визуализировать я это не могу, так что включайте фантазию.

В пятимерном мире так же добавятся новые направления движения, которые называют «ана-ката», получается: «влево-вправо», «вперед-назад», «вверх-вниз» и «ана»-«ката». Представить себе направление движения ана и ката мы не можем, так же как существо в двумерном мире не может представить себе направления вверх и вниз.

В таком мире можно завязать двумерную сферу на узел, в нашем мире сделать это невозможно, показать, соответственно, тоже нельзя. Ну и стул с тремя ножками не сможет стоять в мире с 4 пространственными измерениями, чтобы он был устойчив потребуется 4 или больше ножек.

Ну хорошо, я понимаю, вы вряд ли Вы читаете это, чтобы узнать о узлах и ножках стула, Вас интересует, что будет с нашим миром, если внезапно в него добавить еще одно измерение, вот так по щелчку пальца «тыц» и добавили еще одно пространственное измерение и вот ты уже в 5 измерении, что с тобой будет?

Если коротко то… умрешь конечно же. А еще Земля станет приплюснутой. Сейчас расскажу как именно умрешь и почему земля станет приплюснутой.

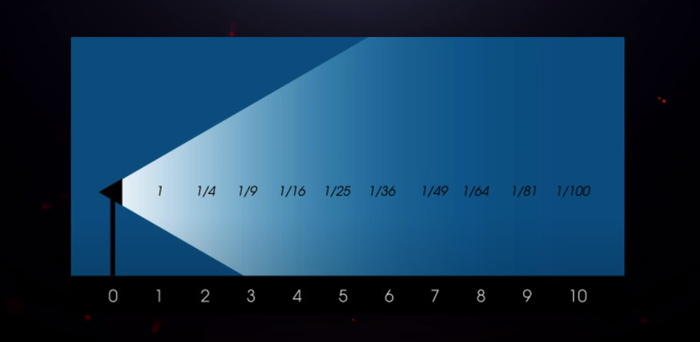
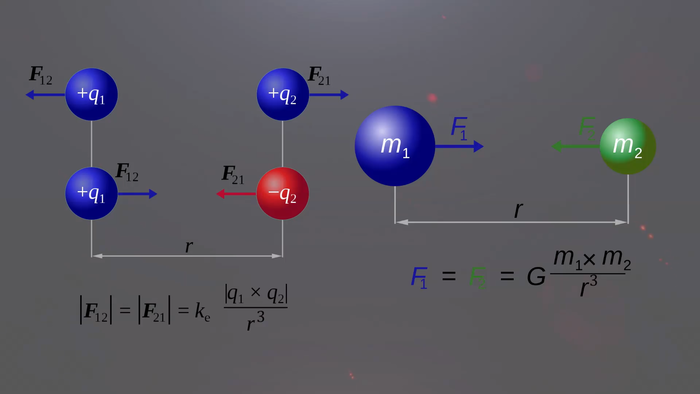
Есть такой закон – закон обратных квадратов, и он тесно связан с размерностью пространства. Возьмем для примера светящий фонарь, интенсивность света в таком случае убывает согласно закону обратных квадратов.

Объект, перемещенный на расстояние в 2 раза большее от источника, получает только четверть той мощности, которую он получал в первоначальном положении. На расстоянии в 3 раза большее от источника – в 9 раз меньше мощности, на расстоянии в 4 раза большее от источника – 16 раз и так далее.

В законе всемирного тяготения сила гравитационного притяжения убывает тоже с квадратом расстояния. В два раза увеличиваем расстояние, сила притяжения уменьшается в 4 раза и так далее. Тоже самое с законом Кулона – сила притяжения или отталкивания заряженных частиц убывает с квадратом расстояния. В 5D мире закон обратных квадратов превращается в закон обратных кубов. Теперь интенсивность света будет падать не с квадратом расстояния, а с кубом расстояния. r^2 в законе Кулона и Законе всемирного тяготения превращается в r^3.

Это все полностью изменит химические элементы из которых мы состоим, некоторые атомы станут нестабильными, радиоактивными, другие наоборот, станут стабильными.

Например, в 5D мире магний был бы благородным газом, а не металлом, то есть некоторые элементы станут менее реактивными, другие более реактивными. Ионизация атомов будет осуществляться при значительно меньших энергиях, да и вообще агрегатное состояние различных элементов будет меняться не так, как в нашем мире, некоторые хим. элементы станут газообразны при комнатной температуре, некоторые затвердеют и такие вот вещи. Думаю, практически бессмысленно вспоминать биологические процессы, благодаря которым мы можем жить, ведь это все поменяется кардинально, мы мгновенно потеряем сознание и умрем, синтез белков, транспортировка различных аминокислот, нейромедиаторов, нервные импульсы, это все либо прекратится, либо изменится до неузнаваемости. Ну и конечно же спектры атомов изменятся, а это значит, что все резко поменяет цвет, что-то станет прозрачным, что-то непрозрачным, да и вообще привычные для нас источники света выглядели бы более тускло из-за r^3, с запахами та же история, правда уже некому будет смотреть и нюхать все это, ведь все живые существа погибнут.

Короче будет происходить полная жесть, что-то будет плавится, что-то превратится в газ, что-то затвердеет, некоторые вещества станут радиоактивными, привычные нам вещи потеряют свои свойства и перестанут работать так, как в нашем мире. Я напомню, что это все в мире, в котором 4 пространственных измерения и одно временное и в котором можно двигаться в направлении ана и ката. Но кроме дополнительного направления появятся также дополнительные степени свободы во вращении. В нашем мире ориентацию тела можно задать тремя углами, в быту это называется «наклон, подъём и поворот», в 5D мире надо представить себе еще 3 дополнительных степени свободы вращения перпендикулярные к 3 вышеупомянутым. Но по идее, на вращение Земли это не должно повлиять, момент импульса сохранится, ведь нужно, чтобы какая-то сила передала момент импульса Земле, чтобы она могла вращаться в какой-то непривычный для нас способ. Конечно Земля изменит свой привычный облик, из-за того, что свойства химических элементов изменятся, но из-за гравитации все должно также удерживаться вокруг центра масс, правда земля довольно быстро вращается, а так как гравитация в 5D мире у нас ослабевает с кубом расстояния, то земля сплюснется и формой будет напоминать что-то типа такого, как на картинке.

Но вообще, появится дополнительное направление, в котором могут двигаться частицы из которых состоит земля, планета начнет превращаться в гиперсферу, представить себе этот процесс, эти метаморфозы которые будут происходить, очень сложно.

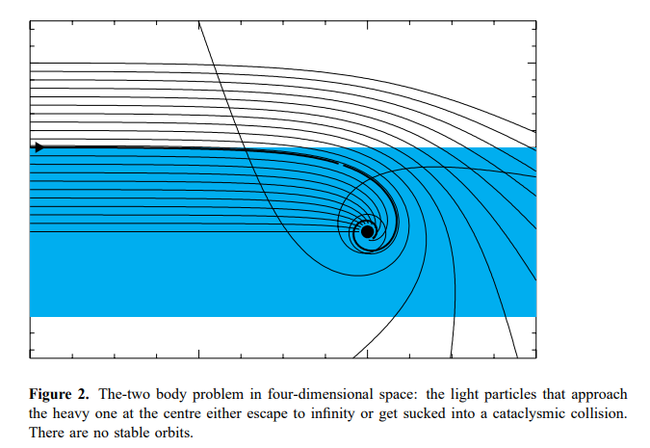
Будут ли происходить термоядерные реакции на солнце, тут под вопросом, но изменения явно произойдут. Но вот что забавно – в пятимерном мире нет стабильных орбит. Вот, посмотрите на график, это моделирование классической задачи двух тел, оказывается, что устойчивых орбит в 5D мире нет, тела либо падают друг на друга, либо улетают в бесконечность, поэтому солнечная система, как и все другие системы, разрушится, некоторые тела упадут на другие тела, а некоторые улетят бороздить просторы галактики.

Казалось бы, следуя логике как с законом обратных квадратов, все квадраты в других уравнениях тоже надо заменить на кубы и получается, что формула эквивалентности массы и энергии в пятимерном пространстве будет работать как Е=мс в кубе, но нет, эта формула, как и множество других, не изменятся в пятимерном пространстве, она, как и множество других формул, не зависит от размерности пространства.

Но даже и без этого всего, мир в 5 мерном пространстве изменится настолько, что в нем не сможет существовать жизнь в том виде, в котором существует в четырехмерном пространстве. Вообще, оказывается, четырехмерный мир – самый простой из возможных и одновременно самый оптимальный для существования в нем жизни, стабильных орбит и химии, какой мы ее знаем.

Книга Кипа Торна, «Интерстеллар. Наука за кадром»

Источник