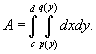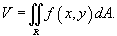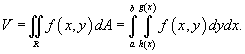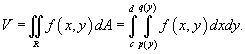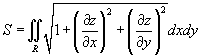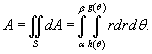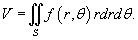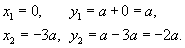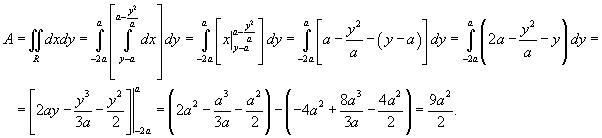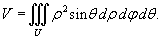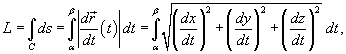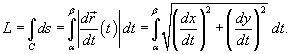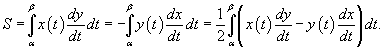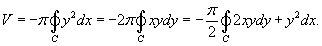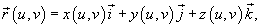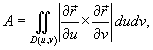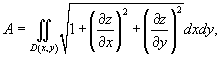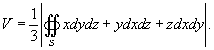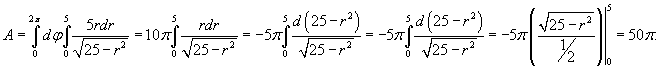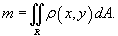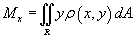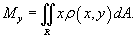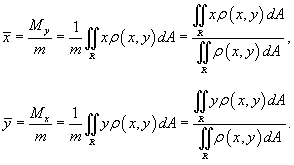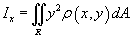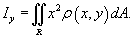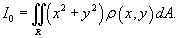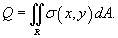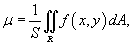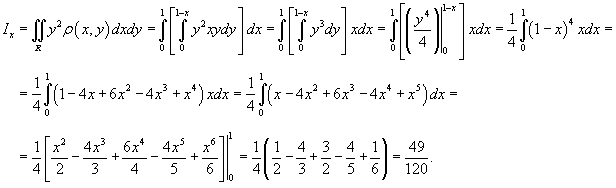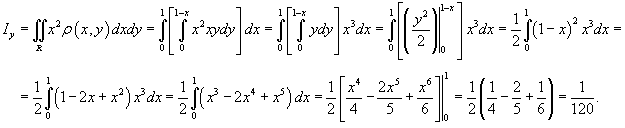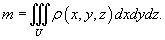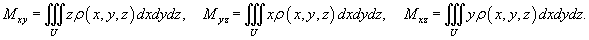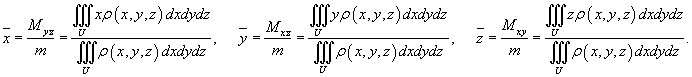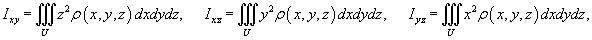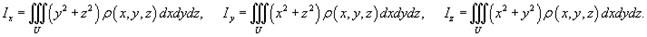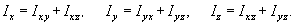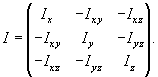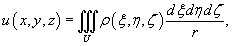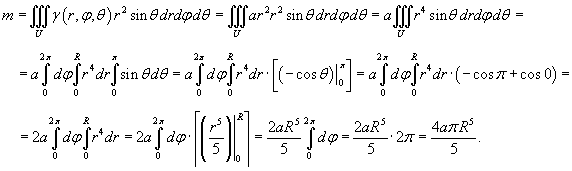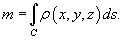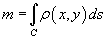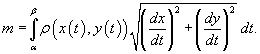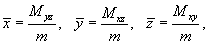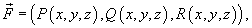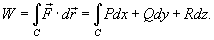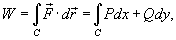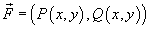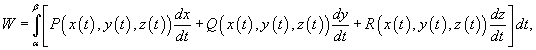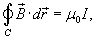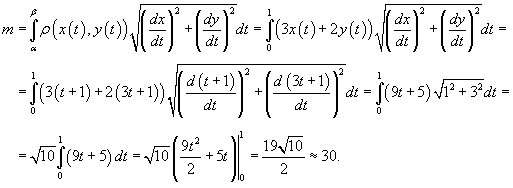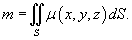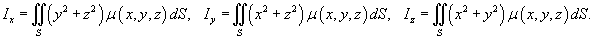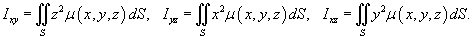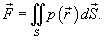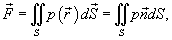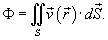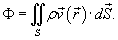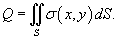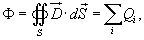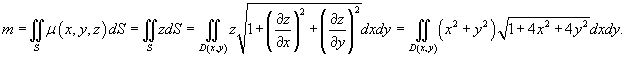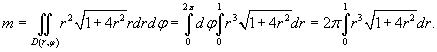геометрические и физические приложения двойного интеграла
Геометрические и физические приложения двойных, тройных, криволинейных и поверхностных интеграло
Главная > Реферат >Математика
1.Геометрические приложения интегралов
1.1 Геометрические приложения двойных интегралов………….. 3
1.2 Геометрические приложения тройных интегралов………….. 5
1.3 Геометрические приложения криволинейных интегралов… 6
1.4 Геометрические приложения поверхностных интегралов….. 8
2. Физические приложения интегралов
2.1 Физические приложения двойных интегралов……………… 10
2.2 Физические приложения тройных интегралов……………… 12
2.3 Физические приложения криволинейных интегралов……. 14
2.4 Физические приложения поверхностных интегралов……… 18
1.Геометрические приложения интегралов
1.1 Геометрические приложения двойных интегралов
1)Площадь плоской фигуры
Площадь области типа I (элементарной относительно оси О y ) (рисунок 1) выражается через повторный интеграл в виде
Аналогично, площадь области типа II (элементарной относительно оси О x ) (рисунок 2) описывается формулой
3) Площадь поверхности
Площадь и объем в полярных координатах
Пусть S является областью, ограниченной линиями (рисунок 3). Тогда площадь этой области определяется формулой
Сначала определим точки пересечения двух заданных линий.
Следовательно, координаты точек пересечения равны
Область R представлена на рисунке 5 выше. Будем рассматривать ее как область типа II. Для вычисления площади преобразуем уравнения границ:
1.2 Геометрические приложения тройных интегралов
Объем тела U в декартовых координатах Oxyz выражается формулой
В цилиндрических координатах объем тела равен
В сферических координатах, соответственно, используется формула
Вычислим объем части шара, расположенной в первом октанте ( x ≥ 0, y ≥ 0, z ≥ 0), и затем умножим результат на 8. Получаем
1.3 Геометрические приложения криволинейных интегралов
Криволинейные интегралы имеют многочисленные приложения в математике, физике и прикладных расчетах. В частности, с их помощью вычисляются
Площадь области, ограниченной замкнутой кривой;
Объем тела, образованного вращением замкнутой кривой относительно некоторой оси.
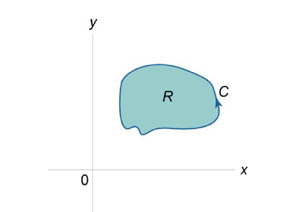
Если кривая C задана в плоскости, то ее длина выражается формулой
Площадь области, ограниченной замкнутой кривой
Здесь предполагается, что обход кривой C производится против часовой стрелки.
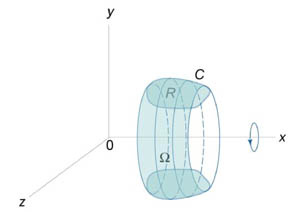
Объем тела, образованного вращением замкнутой кривой относительно оси Ox
1.4 Геометрические приложения поверхностных интегралов
С помощью поверхностных интегралов вычисляются
Объем тела, ограниченного замкнутой поверхностью.
Пусть S является гладкой, кусочно-непрерывной поверхностью. Площадь поверхности определяется интегралом
Если поверхность S задана параметрически с помощью вектора
то площадь поверхности будет равна
где D ( u,v ) − это область, в которой задана поверхность.
Если поверхность S задана в явном виде функцией z ( x,y ), то площадь поверхности выражается формулой
Объем тела, ограниченного замкнутой поверхностью
Площади заданной поверхности равна
Переходя к полярным координатам, находим ответ:
Реферат: Геометрические и физические приложения двойных, тройных, криволинейных и поверхностных интеграло
| Название: Геометрические и физические приложения двойных, тройных, криволинейных и поверхностных интеграло Раздел: Рефераты по математике Тип: реферат Добавлен 05:48:59 10 июля 2011 Похожие работы Просмотров: 2007 Комментариев: 8 Оценило: 3 человек Средний балл: 4 Оценка: неизвестно Скачать | |||||||||||||||||||
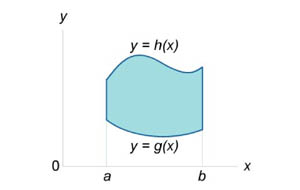 | 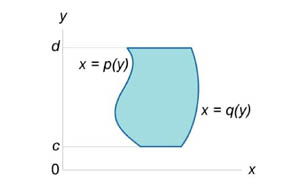 |
| Рис.1 | Рис.2 |
В случае, когда R является областью типа I, ограниченной линиями 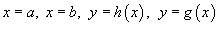
Для области R типа II, ограниченной графиками функций 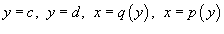
Если в области R выполняется неравенство 
Площадь и объем в полярных координатах
Пусть S является областью, ограниченной линиями 
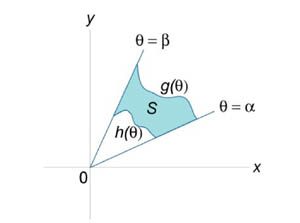 |
| Рис. 3 |
Сначала определим точки пересечения двух заданных линий.
Следовательно, координаты точек пересечения равны
Область R представлена на рисунке 5 выше. Будем рассматривать ее как область типа II. Для вычисления площади преобразуем уравнения границ:
1.2 Геометрические приложения тройных интегралов
Объем тела U в декартовых координатах Oxyz выражается формулой
В цилиндрических координатах объем тела равен
В сферических координатах, соответственно, используется формула
Вычислим объем части шара, расположенной в первом октанте (x ≥ 0, y ≥ 0, z ≥ 0), и затем умножим результат на 8. Получаем
1.3 Геометрические приложения криволинейных интегралов
Криволинейные интегралы имеют многочисленные приложения в математике, физике и прикладных расчетах. В частности, с их помощью вычисляются
· Площадь области, ограниченной замкнутой кривой;
· Объем тела, образованного вращением замкнутой кривой относительно некоторой оси.
Пусть C является гладкой, кусочно-непрерывной кривой, которая описывается вектором 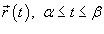
где 
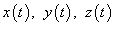
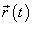
Если кривая C задана в плоскости, то ее длина выражается формулой
Наконец, если кривая C задана в полярных координатах уравнением 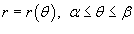
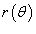

Площадь области, ограниченной замкнутой кривой
Здесь предполагается, что обход кривой C производится против часовой стрелки.
Если замкнутая кривая C задана в параметрическом виде 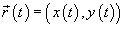
 |  |
| Рис.1 | Рис.2 |
Объем тела, образованного вращением замкнутой кривой относительно оси Ox
1.4 Геометрические приложения поверхностных интегралов
С помощью поверхностных интегралов вычисляются
Пусть S является гладкой, кусочно-непрерывной поверхностью. Площадь поверхности определяется интегралом
Если поверхность S задана параметрически с помощью вектора
то площадь поверхности будет равна
где D (u,v ) − это область, в которой задана поверхность.
Если поверхность S задана в явном виде функцией z (x,y ), то площадь поверхности выражается формулой
Объем тела, ограниченного замкнутой поверхностью
Площади заданной поверхности равна
Переходя к полярным координатам, находим ответ:
2. Физические приложения интегралов
2.1Физические приложения двойных интегралов
Масса и статические моменты пластины
Статический момент пластины относительно оси Ox определяется формулой
Аналогично находится статический момент пластины относительно оси Oy :
Моменты инерции пластины
Момент инерции пластины относительно оси Ox выражается формулой
Аналогично вычисляется момент инерции пластины относительно оси Oy :
Полярный момент инерции пластины равен
Предположим, что электрический заряд распределен по области R в плоскости Oxy и его плотность распределения задана функцией 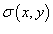
Среднее значение функции
Вычислить моменты инерции треугольника, ограниченного прямыми 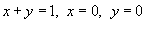
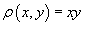
2.2 Физические приложения тройных интегралов
Масса и статические моменты тела
Пусть тело занимает объем U и его объемная плотность в точке M (x,y,z ) задана функцией ρ (x,y,z ). Тогда масса тела m вычисляется с помощью тройного интеграла:
Статические моменты тела относительно координатных плоскостей Oxy, Oxz, Oyz выражаются формулами
Координаты центра тяжести тела вычисляются по формулам:
Моменты инерции тела
Моменты инерции тела относительно координатных плоскостей Oxy, Oxz, Oyz определяются выражениями
а моменты инерции тела относительно координатных осей Ox, Oy, Oz вычисляются по формулам
Как видно, справедливы соотношения
Моментом инерции тела относительно начала координат называется интеграл
Момент инерции относительно начала координат можно выразить через моменты инерции относительно координатных плоскостей:
Если тело вращается вокруг оси, не совпадаюшей с главной осью инерции, то оно будет испытывать вибрации при высоких скоростях вращения. Поэтому, при конструировании таких устройств необходимо, чтобы ось вращения совпадала с одной из главных осей инерции. Например, при замене шин автомобиля проводится их балансировка: небольшие грузики добавляются к колесам, чтобы обеспечить совпадение оси вращения с главной осью инерции и исключить вибрации.
Гравитационный потенциал и сила тяготения
Ньютоновым потенциалом тела в точке P (x,y,z ) называется интеграл
где ρ (ξ,η,ζ ) − плотность тела, и 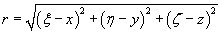
Интегрирование выполняется по всему объему тела. Зная потенциал, можно вычислить силу притяжения материальной точки массы m и заданного распределенного тела с плотностью ρ (ξ,η,ζ ) по формуле
где G − гравитационная постоянная.
2.3 Физические приложения криволинейных интегралов
С помощью криволинейных интегралов вычисляются
2) Центр масс и моменты инерции кривой;
3) Работа при перемещении тела в силовом поле;
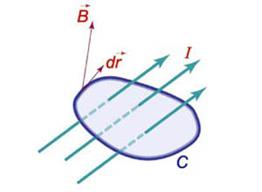
4) Магнитное поле вокруг проводника с током (Закон Ампера);
5) Электромагнитная индукция в замкнутом контуре при изменении магнитного потока (Закон Фарадея).
Рассмотрим эти приложения более подробно с примерами.
Если кривая C задана в параметрическом виде с помощью векторной функции 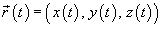
или в параметрической форме
Центр масс и моменты инерции кривой
Моменты инерции относительно осей Ox, Oy и Oz определяются формулами
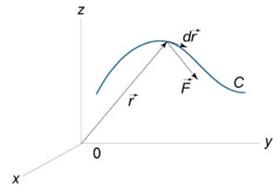
Работа при перемещении тела в силовом поле 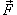
где 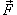
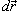
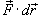
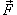
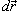
Заметим, что силовое поле 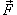
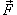
Если векторное поля задано в координатной форме в виде
то работа поля вычисляется по формуле
Где
Если траектория движения C определена через параметр t (t часто означает время), то формула для вычисления работы принимает вид
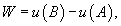
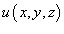
 |  |
| Рис.1 | Рис.2 |
Криволинейный интеграл от магнитного поля с индукцией 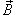
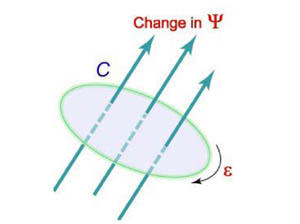 |
| Рис.3 |
Определить массу проволоки, имеющей форму отрезка от точки A (1,1) до B (2,4). Масса распределена вдоль отрезка с плотностью 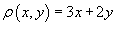
где параметр t изменяется в интервале [0,1]. Тогда масса проволоки равна
2.4 Физические приложения поверхностных интегралов
Поверхностные интегралы применяются во многих прикладных расчетах. В частности, с их помощью вычисляются
Пусть S представляет собой тонкую гладкую оболочку. Распределение массы оболочки описывается функцией плотности 
Центр масс и моменты инерции оболочки
Пусть распределение массы m в тонкой оболочке описывается непрерывной функцией плотности 
− так называемые моменты первого порядка относительно координатных плоскостей x = 0, y = 0 и z = 0, соответственно.
Моменты инерции оболочки относительно осей Ox, Oy, Oz выражаются, соответственно, формулами
Моменты инерции оболочки относительно плоскостей xy, yz, xz определяются формулами
Сила притяжения поверхности
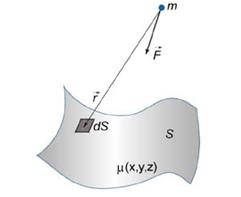 |  |
| Рис.1 | Рис.2 |
Сила притяжения между поверхностью S и точечным телом m определяется выражением
Предположим, что поверхность S задана вектором 
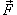

Давление, по определению, действует в направлении вектора нормали к поверхности S в каждой точке. Поэтому, мы можем записать
Поток жидкости и поток вещества
Аналогично, поток векторного поля 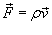
Он численно равен массе вещества, проходящего через поверхность S в единицу времени.
Поток электрического смещения 
где 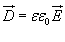
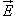

Теорема Гаусса применима к любым замкнутым поверхностям. В случае поверхности с достаточной симметрией, данная теорема упрощает вычисление электрического поля. Теорему Гаусса рассматривают как один из основных постулатов теории электричества. Она входит в систему основных уравнений Максвелла.
Найти массу параболической оболочки, заданной уравнением 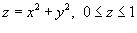
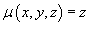
Проекция D (x,y ) параболической поверхности S на плоскость xy представляет собой круг радиусом 1 с центром в начале координат. Следовательно, можно записать
Переходя в подынтегральном выражении к полярным координатам, получаем
Сделаем подстановку 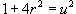
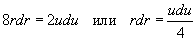

- геометрические и механические приложения определенного интеграла
- геометрические и физические приложения кратных криволинейных и поверхностных интегралов