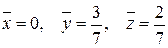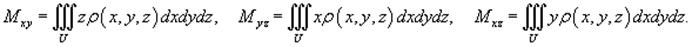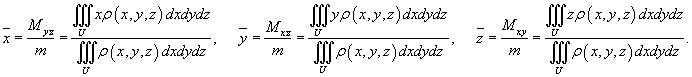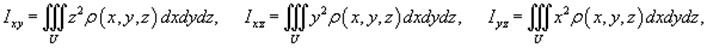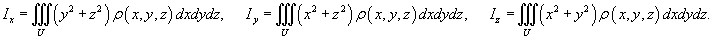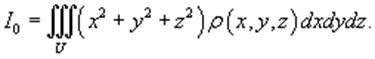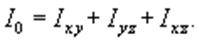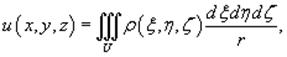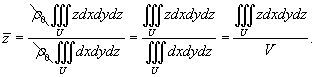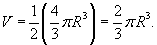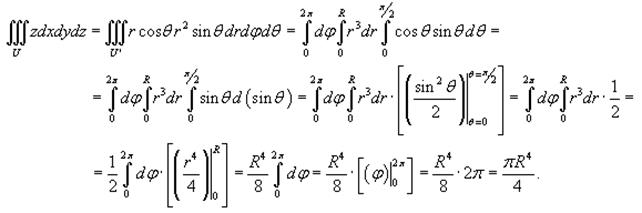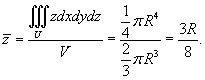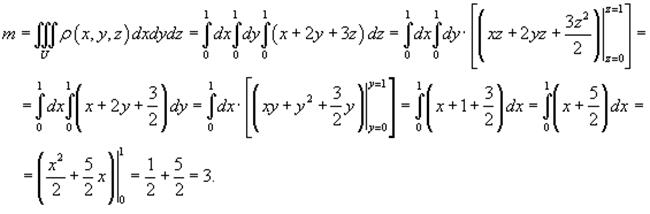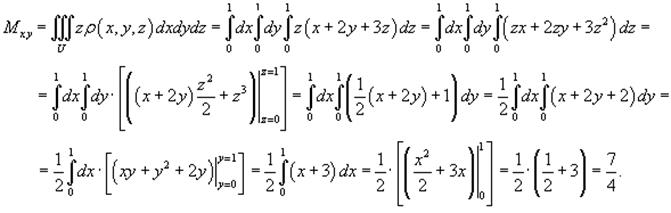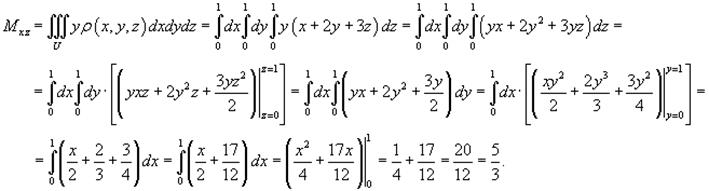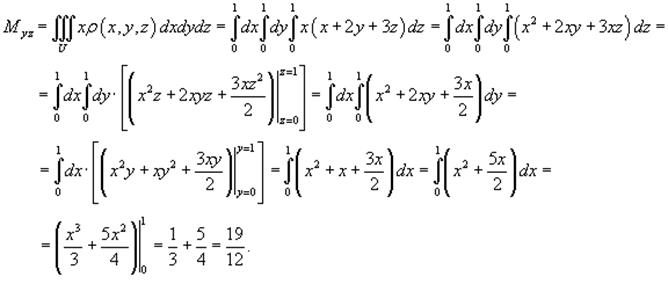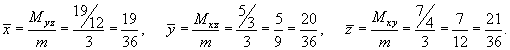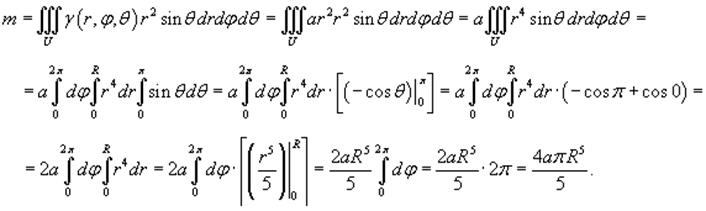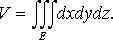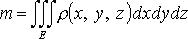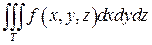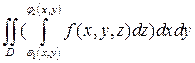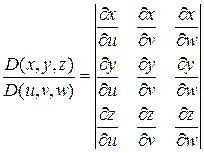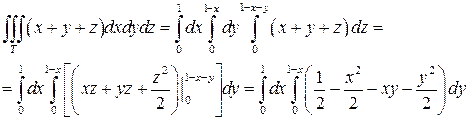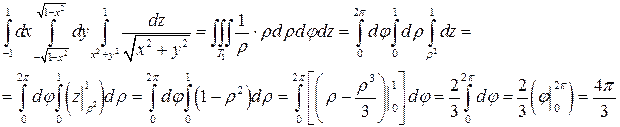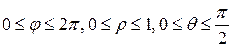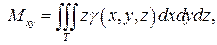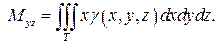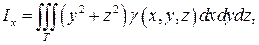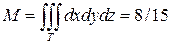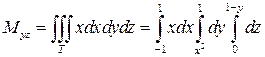геометрические и физические приложения тройного интеграла
Приложения тройного интеграла
Физические приложения тройных интегралов
Масса и статические моменты тела
Пусть тело занимает объем U и его объемная плотность в точке M(x,y,z) задана функцией ρ(x,y,z). Тогда масса тела m вычисляется с помощью тройного интеграла:
Статические моменты тела относительно координатных плоскостей Oxy, Oxz, Oyz выражаются формулами
Координаты центра тяжести тела вычисляются по формулам:
Если тело является однородным с плотностью ρ(x,y,z) = 1 для точек M(x,y,z) в области U, то центр тяжести тела зависит только от геометрии тела и называется центроидом.
Моменты инерции тела
Моменты инерции тела относительно координатных плоскостей Oxy, Oxz, Oyz определяются выражениями
а моменты инерции тела относительно координатных осей Ox, Oy, Oz вычисляются по формулам
Как видно, справедливы соотношения
Моментом инерции тела относительно начала координат называется интеграл
Момент инерции относительно начала координат можно выразить через моменты инерции относительно координатных плоскостей:
Тензор инерции
Используя рассмотренные выше 6 чисел Ix, Iy, Iz, Ixy, Ixz, Iyz, можно составить так называемую матрицу инерции или тензор инерции тела:
Данный тензор является симметричным, и, следовательно, его можно привести к диагональному виду при определенном выборе осей Ox’, Oy’, Oz’. Значения диагональных элементов (после приведения тензора к диагональному виду) называются главными моментами инерции, а указанные направления − собственными векторами или главными осями инерции.
Если тело вращается вокруг оси, не совпадающей с главной осью инерции, то оно будет испытывать вибрации при высоких скоростях вращения. Поэтому, при конструировании таких устройств необходимо, чтобы ось вращения совпадала с одной из главных осей инерции. Например, при замене шин автомобиля проводится их балансировка: небольшие грузики добавляются к колесам, чтобы обеспечить совпадение оси вращения с главной осью инерции и исключить вибрации.
Гравитационный потенциал и сила тяготения
Ньютоновым потенциалом тела в точке P(x,y,z) называется интеграл
где ρ(ξ,η,ζ) − плотность тела, и 
Интегрирование выполняется по всему объему тела. Зная потенциал, можно вычислить силу притяжения материальной точки массы m и заданного распределенного тела с плотностью ρ(ξ,η,ζ) по формуле
где G − гравитационная постоянная.
ПРИМЕРЫ
Пример 1.Найти центроид однородного полушара радиусом R.

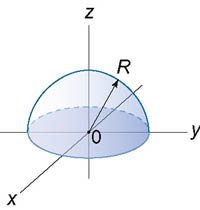
Вычислим координату центра тяжести 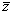
Поскольку полушар однородный, то полагаем ρ(x,y,z) = ρ0. Тогда
В знаменателе через V обозначен объем полушара, равный
Остается вычислить тройной интеграл 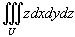
Таким образом, координата центра тяжести 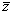
Пример 2.Определить массу и координаты центра тяжести единичного куба
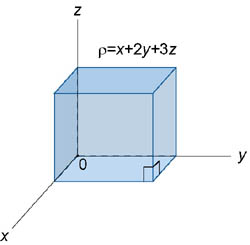
Решение.
Сначала вычислим массу куба:
Теперь вычислим статические моменты Mxy, Mxz, Myz.
Вычисляем координаты центра тяжести куба:
Пример 3.Найти массу шара радиуса R, плотность γ которого пропорциональна квадрату расстояния от центра.
Приложения тройного интеграла
( 
Вычисление тройных интегралов: теория и примеры
Понятие тройного интеграла
Записывается тройной интеграл так:

Здесь V – пространственная (трёхмерная) фигура, ограниченная плоскостями, выражения которых (равенства) даны в задании вычисления тройного интеграла. V называют также замкнутой ограниченной областью трёхмерного пространства.

Если функция f(M) = f(x, y, z) непрерывна, то будет существовать предел интегральных сумм вида, указанного выше. Этот предел и называется тройным интегралом.
Вычисление тройного интеграла путём уменьшения кратности
Как и в случае двойных интегралов, вычисление тройных интегралов сводится к вычислению интегралов меньшей кратности.
Мы будем рассматривать только правильные области.
Переходя от двойного интеграла к повторному, получаем следующую формулу для вычисления тройного интеграла:
Таким образом, для вычисления тройного интеграла требуется последовательно вычислить три определённых интеграла.
Вычисляются эти интегралы от самого внутреннего (по переменной z) к самому внешнему (по переменной x). Для удобства восприятия последовательности вычислений три «вложенных» интеграла можно записать так:

Из этой записи уже однозначно видно, что:
Пример 1. Пусть от тройного интеграла можно перейти к повторному интегралу

последовательности трёх определённых интегралов. Вычислить этот повторный интеграл.
Решение. Вычисление повторного интеграла всегда начинается с последнего интеграла:



Ответ: данный повторный интеграл и соответствующий ему тройной интеграл равен 10.
Пример 2. Вычислить тройной интеграл

Решение. Пределы интегрирования для всех трёх определённых интегралов однозначно заданы уравнениями поверхностей, ограничивающих параллелепипед. Поэтому сразу сводим данный тройной интеграл к последовательности трёх определённых интегралов:



Пример 3. Вычислить тройной интеграл

Сводим данный тройной интеграл к последовательности трёх определённых интегралов:


Ответ: данный тройной интеграл равен 1/8.
Вычислить тройной интеграл самостоятельно, а затем посмотреть решение
Пример 4. Вычислить тройной интеграл

Расстановка пределов интегрирования при переходе к последовательности трёх интегралов
Начнём с примера «пострашнее», чтобы почувствовать «обстановку, приближенную к боевой».


Теперь посмотрим на эллипсоид сверху. Здесь его ограничивает поверхность, являющаяся той части поверхности эллипсоида, которая расположена выше оси xOy. Следовательно, нужно выразить из уравнения эллипсоида z и полученное выражение будет верхним пределом интегрирования по переменной z:

Проекцией эллипсоида на плоскость xOy является эллипсоид. Его уравнение:

Чтобы получить нижний предел интегрирования по переменной y, нужно выразить y из уравнения эллипсоида и взять полученное выражение со знаком минус:

Для верхнего предела интегрирования по переменной y то же выражение со знаком плюс:

Таким образом, последовательность интегралов для вычисления объёма эллипсоида следующая:

Пример 6. Вычислить тройной интеграл

Решение. «Курортный» пример по сравнению с примером 5, так как пределы интегрирования по «игрек» и «зет» определены однозначно. Но придётся разобраться с пределами интегрирования по «иксу». Проекцией области интегрирования на плоскость xOy является трапеция ABCD.



Ответ: данный тройной интеграл равен 43.
Пример 7. Вычислить тройной интеграл

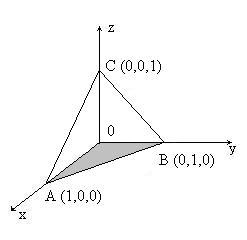
Решение. Область V (пирамида MNRP) является правильной. Проекцией области V на плоскость xOy является треугольник AOB.
Сведём данный тройной интеграл к последовательности трёх определённых интегралов:



Ответ: данный тройной интеграл равен 2.
Замена переменных в тройном интеграле и цилиндрические координаты
Для того, чтобы в тройном интеграле перейти к цилиндрическим координатам, нужно подынтегральную функцию выразить в виде функции переменных r, φ, z:

То есть переход от прямогольных координат к цилиндрическим осуществляется следующим образом:

Тройной интеграл в цилиндрических координатах вычисляется так же как и в декартовых прямоугольных координатах, путём преобразования в последовательность трёх определённых интегралов:
Пример 8. Вычислить тройной интеграл
Ответ: данный тройной интеграл равен π/6.
Тройной интеграл в сферических координатах
Сферические координаты связаны с прямоугольными декартовыми координатами соотношениями
Элемент объёма в сферических координатах выражается следующим образом:

Таким образом, переход от прямоугольных декартовых координат в тройном интеграле к сферическим координатам осуществляется по формуле:
Пример 9. Вычислить тройной интеграл
Учитывая, что 
Расставим пределы интегрирования и перепишем последний полученный интеграл в виде трёх повторных интегралов. По рисунку видно, что 


Приложения тройного интеграла
Вычисление объёма тела. Объём области V равен тройному интегралу по этой области, если подынтегральная функция равна 1:

Вычисление массы неоднородного тела. Массу неоднородного тела с плотностью ρ = ρ(x, y, z) можно вычислить по формуле:

Пример 10. Вычислить объём тела, ограниченного поверхностями 


Таким образом, записываем тройной интеграл в цилиндрических координатах и вычисляем его:
Тройные интегралы



Пусть функция u=f(x,y,z) определена и непрерывна в ограниченной замкнутой области T пространства Oxyz. Разобьем область T произвольным образом на n областей V1, V2,…, Vn, которые назовем элементарными областями. В каждой из элементарных областей произвольным образом выберем по точке 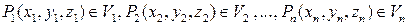
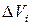
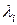
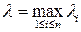
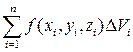
Если существует предел выражения (7) при 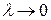
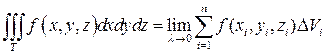
Свойства тройных интегралов аналогичны свойствам двойных интегралов.
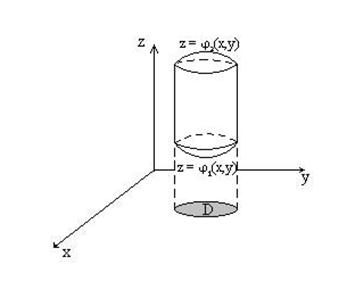
Вычисление тройных интегралов сводится к вычислению повторных интегралов следующим образом. Пусть область T ограничена снизу поверхностью 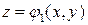
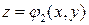
Пусть функция u=f(x,y,z) определена и интегрируема в области T и для любых точек 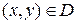
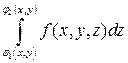
Тогда существует интеграл
и справедлива формула
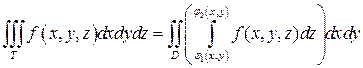
Теорема (о замене переменных в тройном интеграле). Пусть выполняются следующие условия:
1) функции x=x(u,v,w), y=y(u,v,w) и z=z(u,v,w) таковы, что каждой точке с координатами (x,y,z) из области T соответствует единственная точка с координатами (u,v,w) из области T1 и наоборот;
Тогда справедлива формула:
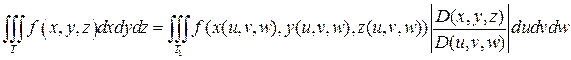
— якобиан перехода от декартовых координат к криволинейным координатам.
Частным случаем криволинейных координат для тройного интеграла являются цилиндрические и сферические координаты.
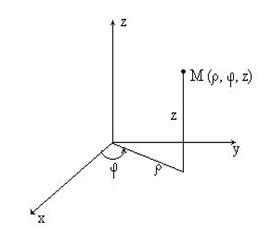
1) В случае цилиндрических координат положение точки M в пространстве определяется тремя числами 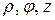
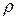
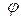
Имеют место формулы:
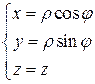
якобиан перехода от декартовых координат к цилиндрическим равен 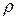
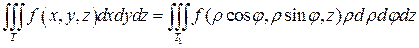
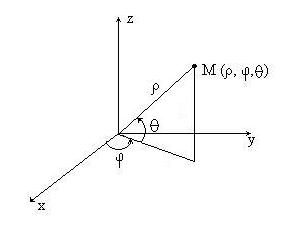
2) В случае сферических координат положение точки M в пространстве определяется тремя числами 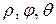
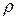
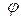
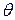
Имеют место формулы:
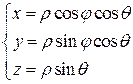
якобиан перехода от декартовых координат к сферическим равен 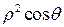
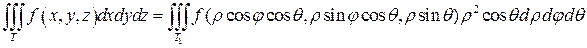
Задание 1. Вычислить интеграл:

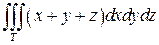
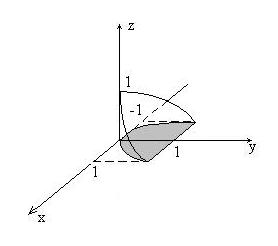
Решение. Изобразим область интегрирования (рис.9).
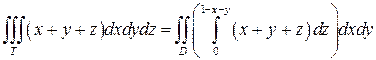
Записывая двойной интеграл по области D через повторный интеграл, получим:
И, наконец, вычислим полученный повторный интеграл:
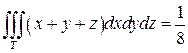
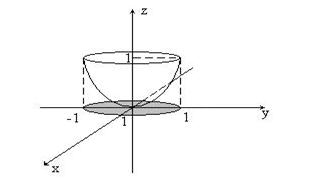
Задание 2. Перейдя к цилиндрическим координатам, вычислить интеграл:
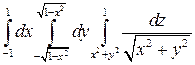
Решение.Изобразим область интегрирования (рис.10).
и применим формулу (11). Так как 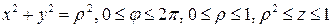
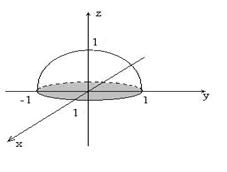
Задание 3. Переходя к сферическим координатам, вычислить интеграл:
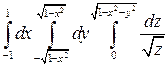
Решение. Область интегрирования T есть полушар 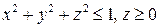
Найдем пределы изменения сферических координат для области T1:
Следовательно, по формуле (12) имеем:
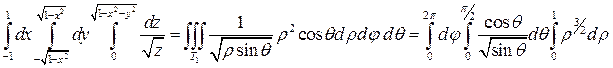
Вычислив полученный тройной интеграл, получим:
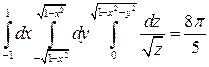
Приложения кратных интегралов
1. Геометрические приложения двойных интегралов
Площадь S плоской области (фигуры) D выражается в зависимости от рассматриваемой системы координат, следующими интегралами:
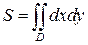
— в декартовых координатах,
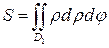
— в полярных координатах.
Пусть гладкая поверхность задана уравнением z=f(x,y). Тогда площадь части этой поверхности, проектирующейся в область D плоскости Oxy, равна:
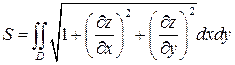
Пусть область T ограничена снизу плоскостью z=0, сверху – непрерывной поверхностью z=f(x,y) и с боков прямой цилиндрической поверхностью. Если проекцией области T на плоскость Oxy является область D, то объем V области T выражается интегралом
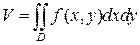
2. Механические приложения двойных интегралов.
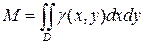
Статические моменты Mx и My этойпластинки относительно осей Ox и Oy
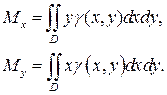
Координаты центра масс 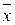
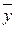
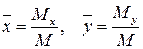
Моменты инерции пластинки относительно осей Ox и Oy соответственно равны:
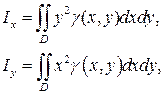
а момент инерции пластинки относительно начала координат равен:
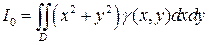
Заметим, что если рассматриваемая пластина однородна, то в приведенных формулах следует положить 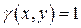
3. Геометрические приложения тройного интеграла
Объем V пространственной области T равен:
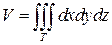
4.Механические приложения тройных интегралов. Масса M тела с плотностью 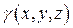
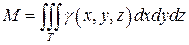
Статические моменты Mxy, Mxz, Myz тела относительно координатных плоскостей выражаются интегралами:
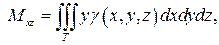
Координаты центра масс тела T определяются следующим образом:
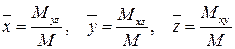
Моменты инерции тела относительно осей координат соответственно равны:
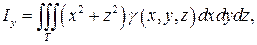
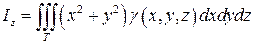
Заметим, что если рассматриваемое тело однородно, то в приведенных формулах следует положить 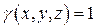
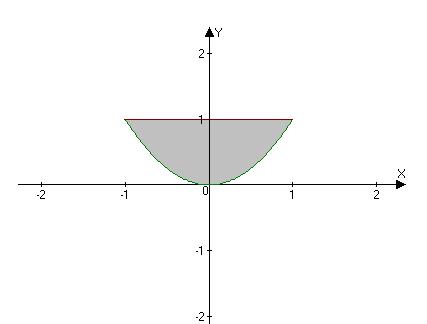
Задание 1. Найти объем тела, ограниченного поверхностями:
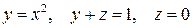
Решение. Данное тело ограничено снизу плоскостью z=0, сверху плоскостью y+z=1 и с боков цилиндром 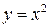
Проекцией рассматриваемого тела является область D (рис. 12б).
Найдем объем нашего тела двумя способами:
1) с помощью двойного интеграла;
2) с помощью тройного интеграла.
В первом случае воспользуемся формулой (16). В нашем случае f(x,y)=1-y.
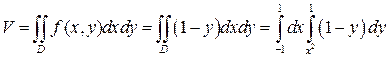
Вычисляем полученный повторный интеграл:
Теперь найдем значение объема данного тела с помощью тройного интеграла. Для этого воспользуемся формулой (22). Имеем:
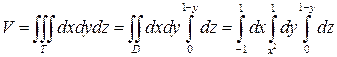
Вычисляем полученный тройной интеграл:
Задание 2. Найти координаты центра масс однородного тела, ограниченного поверхностями 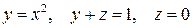
Решение. Данное тело изображено на рис.12а. Чтобы найти координаты центра масс рассматриваемого тела, воспользуемся формулами (25).
Найдем сначала массу тела. Для этого применим формулу (23) при 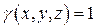
(это интеграл мы вычисляли в предыдущем примере).
Вычислим теперь статические моменты Mxy, Mxz, Myz рассматриваемого тела относительно координатных плоскостей. Для этого воспользуемся формулами (24) при 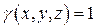
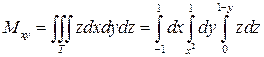
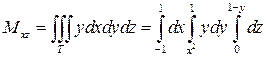
Вычислив полученные тройные интегралы, имеем:
Следовательно, координаты центра масс данного тела равны: