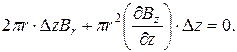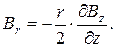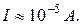гиромагнитное отношение в сгс
В физика, то гиромагнитное отношение (также иногда известный как магнитогирическое соотношение [1] в других дисциплинах) частицы или системы является соотношение своего магнитный момент к его угловой момент, и его часто обозначают символом γ, гамма. Его SI единица радиан в секунду на тесла (радс −1 ⋅T −1 ) или, что то же самое, кулон на килограмм (C⋅kg −1 ).
Часто используется термин «гиромагнитное отношение». [2] как синоним разные но тесно связанная величина, грамм-фактор. В грамм-фактор, в отличие от гиромагнитного отношения, равен безразмерный. Подробнее о грамм-фактор см. ниже или в статье грамм-фактор.
Содержание
Ларморова прецессия
Любая свободная система с постоянным гиромагнитным отношением, например жесткая система зарядов, ядро, или электрон, при размещении во внешнем магнитное поле B (измеряется в теслах), который не совпадает с его магнитный момент, буду прецессия в частота ж (измеряется в герц), которое пропорционально внешнему полю:
По этой причине значения γ/(2π), в единицах герц на тесла (Гц / Т), часто указываются вместо γ.
Эвристический вывод
Модель вращающегося электрона, которую мы используем при выводе, имеет очевидную аналогию с гироскопом. Для любого вращающегося тела скорость изменения момента количества движения J < displaystyle mathbf 

Частота угловой прецессии имеет важное физическое значение: это угловая циклотронная частота, резонансная частота ионизированной плазмы, находящейся под действием статического конечного магнитного поля, когда мы накладываем высокочастотное электромагнитное поле.
Для классического вращающегося тела
Рассмотрим заряжен тело, вращающееся вокруг оси симметрии. Согласно законам классической физики, он обладает как магнитным дипольным моментом, так и угловым моментом, обусловленным его вращением. Можно показать, что пока его заряд и масса распределены одинаково (например, оба распределены равномерно), его гиромагнитное отношение равно
куда q это его заряд и м это его масса. Вывод этого соотношения следующий:
Для изолированного электрона
Изолированный электрон имеет угловой момент и магнитный момент, возникающий из вращение. Хотя спин электрона иногда визуализируется как буквальное вращение вокруг оси, его нельзя отнести к массе, распределенной идентично заряду. Вышеупомянутое классическое соотношение не выполняется, давая неверный результат безразмерным фактором, называемым электронным грамм-фактор, обозначенный грамме (или просто грамм когда нет риска запутаться):
Гиромагнитное отношение для самовращающегося электрона в два раза больше, чем для вращающегося электрона.
В рамках релятивистской квантовой механики
Гиромагнитное отношение электронов определяется NIST. [4] [5] [6] в качестве
В грамм-фактор и γ полностью согласуются с теорией; видеть Прецизионные испытания QED для подробностей.
Гиромагнитный фактор как следствие теории относительности
Физические частицы со спином 1/2, которые не могут быть описаны линейным калиброванным уравнением Дирака, удовлетворяют калиброванному уравнению Клейна – Гордона, расширенному грамм е / 4 σ μν Fμν срок согласно, [8]
Здесь, 1 / 2 σ μν и F μν обозначают генераторы группы Лоренца в пространстве Дирака, а электромагнитный тензор соответственно, а А μ это электромагнитный четырехпотенциальный. Пример такой частицы, [8] является компаньоном спина 1/2 к спину 3/2 в D (1/2,1) ⊕ D (1,1/2) пространство представления группы Лоренца. Было показано, что эта частица характеризуется грамм = −2/3 и, следовательно, вести себя как истинно квадратичный фермион.
Для ядра
Наиболее распространенные ядра, такие как 1 Рука 13 C имеют положительные гиромагнитные отношения. [9] [10] Приблизительные значения для некоторых распространенных ядер приведены в таблице ниже. [12] [13]
Гиромагнитное отношение
Гиромагни́тное отноше́ние (магнитомехани́ческое отноше́ние) — отношение дипольного магнитного момента элементарной частицы (или системы элементарных частиц) к её механическому моменту.
Для различных состояний атомной системы гиромагнитное отношение определяется формулой:
В случае ядер, за единицу гиромагнитного отношения принимают величину:
Согласно классической теории, гиромагнитное отношение является коэффициентом пропорциональности между угловой скоростью прецессии магнитного момента, помещённого во внешнее магнитное поле, и вектором магнитной индукции.
В квантовой теории гиромагнитным отношением определяется величина расщепления уровней в эффекте Зеемана.
См. также
Ссылки
Полезное
Смотреть что такое «Гиромагнитное отношение» в других словарях:
ГИРОМАГНИТНОЕ ОТНОШЕНИЕ — то же, что магнитомеханическое отношение … Большой Энциклопедический словарь
ГИРОМАГНИТНОЕ ОТНОШЕНИЕ — (см. МАГНИТОМЕХАНИЧЕСКОЕ ОТНОШЕНИЕ). Физический энциклопедический словарь. М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983 … Физическая энциклопедия
гиромагнитное отношение — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN gyromagnetic ratio … Справочник технического переводчика
гиромагнитное отношение — то же, что магнитомеханическое отношение. * * * ГИРОМАГНИТНОЕ ОТНОШЕНИЕ ГИРОМАГНИТНОЕ ОТНОШЕНИЕ, то же, что магнитомеханическое отношение (см. МАГНИТОМЕХАНИЧЕСКОЕ ОТНОШЕНИЕ) … Энциклопедический словарь
гиромагнитное отношение — giromagnetinis santykis statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. gyromagnetic coefficient; gyromagnetic ratio vok. gyromagnetisches Verhältnis, n;… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
гиромагнитное отношение — giromagnetinis santykis statusas T sritis fizika atitikmenys: angl. gyromagnetic ratio vok. gyromagnetisches Verhältnis, n rus. гиромагнитное отношение, n pranc. rapport gyromagnétique, m … Fizikos terminų žodynas
Гиромагнитное отношение — отношение магнитного момента атомных частиц (электронов, протонов, нейтронов, атомных ядер и т.д.) к их моменту количества движения. Подробнее см. Магнитомеханическое отношение … Большая советская энциклопедия
ГИРОМАГНИТНОЕ ОТНОШЕНИЕ — то же, что магнитомеханическое отношение … Большой энциклопедический политехнический словарь
ГИРОМАГНИТНОЕ ОТНОШЕНИЕ — то же, что магнитомеханическое отношение … Естествознание. Энциклопедический словарь
Гиромагнитное соотношение
СОДЕРЖАНИЕ
Ларморовая прецессия [ править ]
Эвристический вывод [ править ]
Для классического вращающегося тела [ править ]
Рассмотрим заряженное тело, вращающееся вокруг оси симметрии. Согласно законам классической физики, он обладает как магнитным дипольным моментом, так и угловым моментом, обусловленным его вращением. Можно показать, что до тех пор, пока его заряд и масса распределены одинаково (например, оба распределены равномерно), его гиромагнитное отношение равно
Для изолированного электрона [ править ]
Гиромагнитное отношение для самовращающегося электрона в два раза больше, чем для вращающегося электрона.
В рамках релятивистской квантовой механики
Гиромагнитное отношение электронов определяется NIST [4] [5] [6] как
Гиромагнитный фактор как следствие теории относительности [ править ]
Поскольку гиромагнитный фактор, равный 2, следует из уравнения Дирака, часто ошибочно полагать, что g- фактор 2 является следствием теории относительности; это не так. Множитель 2 может быть получен путем линеаризации как уравнения Шредингера, так и релятивистского уравнения Клейна – Гордона (которое приводит к уравнению Дирака). В обоих случаях получается 4- спинор и для обеих линеаризаций g- фактор оказывается равным 2; Следовательно, множитель 2 является следствием зависимости волнового уравнения от первой (а не второй) производной по пространству и времени. [7]
Физические частицы со спином 1/2, которые не могут быть описаны линейным калиброванным уравнением Дирака, удовлетворяют калиброванному уравнению Клейна – Гордона, расширенному функцией g е / 4 σ μν F μν член согласно, [8]
Для ядра [ править ]
Наиболее распространенные ядра, такие как 1 H и 13 C, имеют положительные гиромагнитные отношения. [10] [11] Приблизительные значения для некоторых распространенных ядер приведены в таблице ниже. [12] [13]
Магнитный момент атома. Гиромагнитное отношение



Рис. 2. Круговой контур с током в неоднородном поле
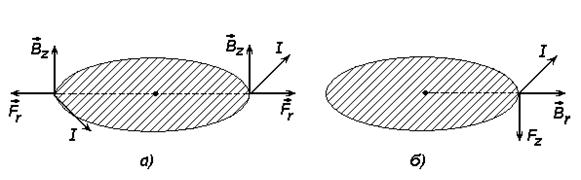
Если поле неоднородно, то кроме сил, растягивающих или сжимающих кольцо, появляются силы, направленные в данной конфигурации вниз (рис. 3).
Рис. 3.43. Силы, действующие на кольцо с током в магнитном поле:
в однородном поле силы направлены вдоль радиуса и растягивают контур (а), в неоднородном поле (б) появляется составляющая Вr магнитной индукции и появляется сила, действующая вдоль оси Z
Так как поле симметрично, то результирующая всех сил, действующих на элементы с током в направлении оси 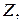
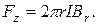
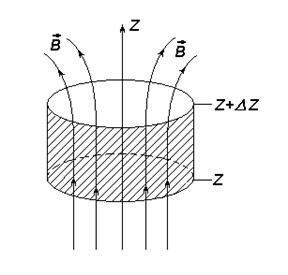
Для вычисления составляющей 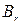
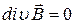
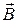
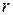
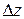
С точностью до членов первого порядка малости имеем:
Первое слагаемое в этом выражении определяет величину потока через боковую поверхность цилиндра. Второе — представляет величину результирующего потока через основания цилиндра.
Отсюда вытекает, что
Рис.4. К вычислению потока вектора
Следовательно, величину силы, действующей на контур в вертикальном направлении, можно выразить следующим образом:
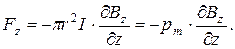
Магнитный момент кольца направлен вверх, а сила, действующая на кольцо, направлена вниз. Очевидно, что, изменив направление тока, мы изменим и направление силы.
Итак, мы можем сделать следующее заключение.
1. Если магнитный момент параллелен вектору 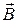
2. Если магнитный момент антипараллелен вектору 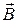
3.Если поле однородное, то сила, действующая в вертикальном направлении, равна нулю.
Теперь у нас появляется возможность объяснить результаты опытов, описанных выше, по крайней мере, на качественном уровне. Можно предположить, что вещество, втягивающееся в соленоид, содержит частицы, магнитные моменты которых параллельны вектору 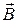
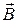
Теперь нам нужно понять: почему в одних веществах эти моменты параллельны вектору 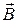
сделать.
Достаточно очевидно, что поведение магнетика в магнитном поле должно быть связано с внутренней структурой самого вещества. Поскольку вещество состоит из атомов и молекул, то, следует, оставаясь в рамках классической физики, вновь обратиться к модели атома.
Атом любого элемента является электронейтральным. Положительный заряд атома сосредоточен в ядре, а отрицательный заряд определяется электронами, число которых в точности равно числу протонов. Электроны являются материальными точками, имеющими заряд 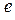
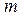
Движение электрона по орбите представляет собой электрический ток. Поэтому электрон, вращающийся по орбите, создает магнитное поле. Другими словами, это приводит к появлению магнитного момента атома.
В рамках классической модели возможное наличие магнитного момента атома обусловлено лишь движением электронов по орбите. В классической физике это является единственным элементом, определяющим поведение атома в магнитном поле.
Для введения основных понятий рассмотрим атом водорода, в состав которого входит один протон и, движущийся вокруг него по круговой орбите радиуса 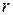
Вычислим силу кругового тока, обусловленного движением электрона по круговой орбите. По определению, сила тока — это количество заряда, протекшего через поперечное сечение за единицу времени. В данном случае электрон за 1 секунду пересечет воображаемое сечение 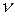
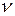
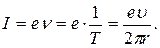
Здесь 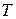
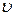
В атоме водорода электрон вращается вокруг ядра с частотой, равной примерно 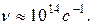
Магнитный момент электрона, обусловленный вращением вокруг ядра, равен:
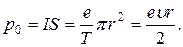
Направление вектора 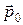
Движущийся по круговой орбите электрон обладает моментом импульса, который равен:
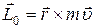
где 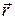
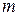
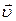
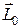
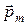
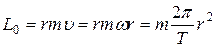
Здесь мы использовали связь линейной 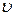
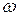
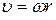
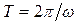
Теперь нетрудно найти отношение:
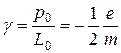
Это отношение магнитного момента электрона к его механическому моменту количества движения называется гиромагнитным (магнитомеханическим) отношением орбитальных моментов электрона. Мы считали, что электрон движется по круговой орбите, но можно показать, что такое же соотношение справедливо и при движении электрона по эллиптической орбите.
Соотношение (6) сыграло фундаментальную роль в развитии всей физики. Гиромагнитное отношение указывает на наличие связи между магнитными и механическими свойствами магнетика. Действительно, если изменились его магнитные свойства, то это должно привести к изменению механических свойств. Справедливо и обратное — изменение механических свойств должно привести к намагничению магнетика.
Впервые в опытах Эйнштейна и де Гааза было показано, что намагничение магнетика в виде железного стержня, помещенного в магнитное поле соленоида, приводит к его вращению. В опытах Барнетта было установлено, что быстрое вращение железного образца приводит к его намагничению. Мы намеренно выделили материал магнетика. Результаты этих опытов позволили определить значение гиромагнитного отношения для железа. Оказалось, что это значение примерно в два раза больше, чем это следует из формулы (6).
Эти данные показывают, что магнитные свойства железа нельзя объяснить наличием лишь орбитальных магнитных моментов электронов. Дальнейший ход развития физики привел к необходимости высказать гипотезу о наличии у электрона собственного внутреннего механического момента количества движения. Этот момент получил название спин электрона. На первом этапе электрон представлялся в виде заряженного вращающегося шара. Отсюда и появилось название спин (to spin — вращаться). Было показано, что значение собственного гиромагнитного отношения для электрона в атоме равно
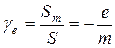
Весь ход развития современной физики полностью подтвердил гипотезу о спине. В настоящее время под спином следует понимать внутреннее свойство самого электрона, такое же как, например, его масса и заряд.
Таким образом, полный механический момент электрона 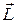
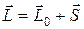
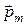
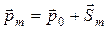
На примере атома водорода мы ввели понятия момента количества движения одного электрона, его спина и определили гиромагнитное соотношение. Однако одним электроном обладает только атом простейшего элемента — водорода. Для других элементов количество электронов определяется зарядовым числом 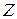
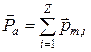
где 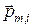
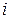
о строении материи, чем изучение поведения вещества в электрических
полях.