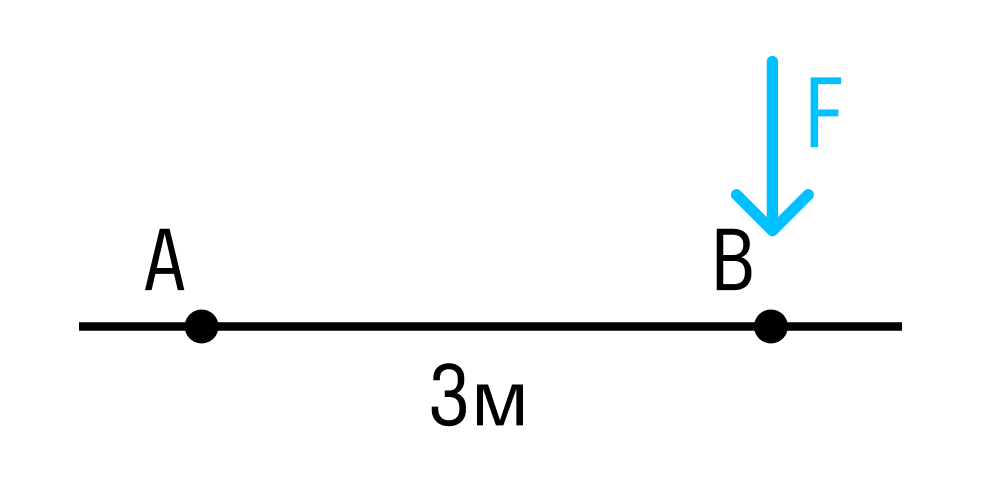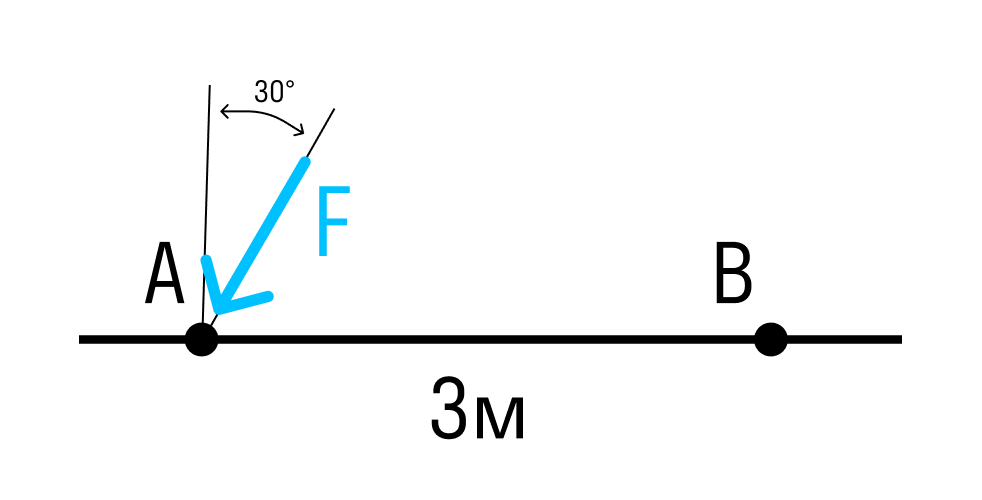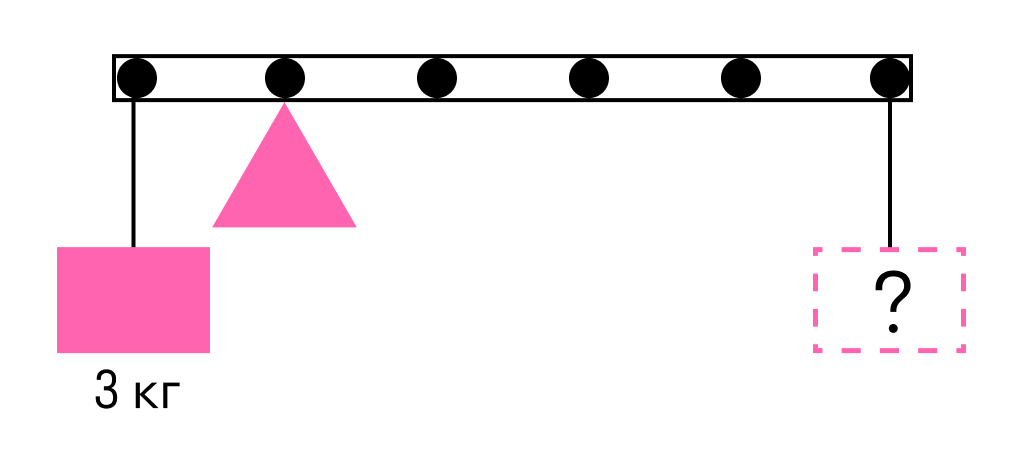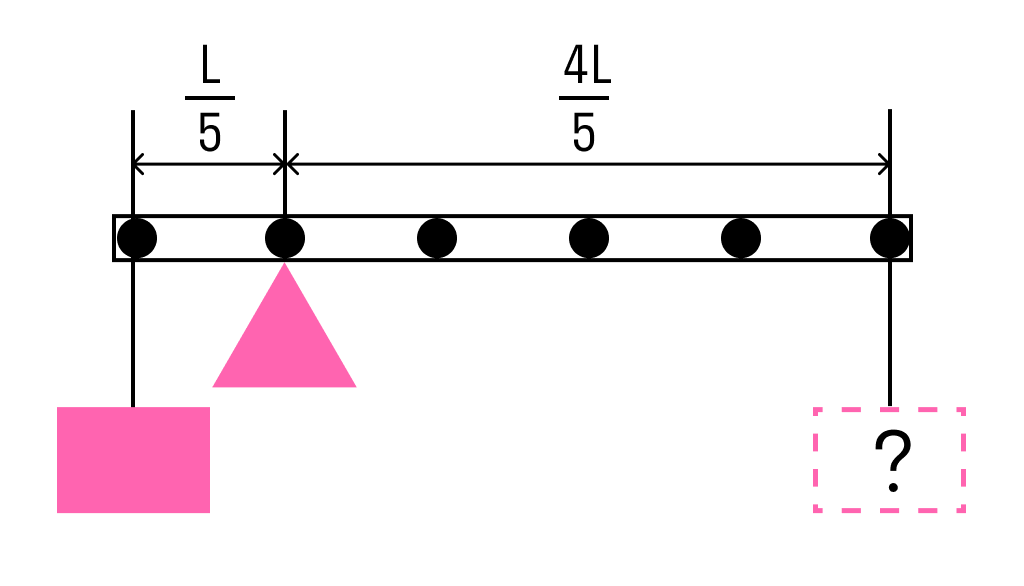измеряется в ньютонах что это
Ньютон
Ньютон.
Ньютон – единица измерения силы в Международной системе единиц (СИ). Имеет русское обозначение – Н и международное обозначение – N.
Другие единицы измерения
Ньютон, как единица измерения:
Ньютон – единица измерения силы в Международной системе единиц (СИ), названная в честь английского физика Исаака Ньютона. Ньютон – производная единица.
Ньютон как единица измерения имеет русское обозначение – Н и международное обозначение – N.
Исходя из второго закона Ньютона сила в 1 ньютон (Н) определяется как сила, изменяющая за 1 секунду скорость тела массой 1 кг на 1 м/с в направлении действия силы.
Исходя из представленных определений можно обнаружить связь ньютона с силой тяжести. Оказывается на тело весом в 102 грамма действует сила тяжести как раз в 1 ньютон, а следовательно сила тяжести действующая на тело массой 1 килограмм равна 9,8 Н.
Применение ньютона:
В ньютонах измеряют силу.
Представление ньютона в других единицах измерения – формулы:
Через основные единицы системы СИ ньютон выражается следующим образом:
Перевод ньютона в другие единицы измерения:
1 Н ≈ 0,10197162 кгс.
Кратные и дольные единицы ньютона:
Кратные и дольные единицы образуются с помощью стандартных приставок СИ.
| Кратные | Дольные | ||||||
| величина | название | обозначение | величина | название | обозначение | ||
| 10 1 Н | деканьютон | даН | daN | 10 −1 Н | дециньютон | дН | dN |
| 10 2 Н | гектоньютон | гН | hN | 10 −2 Н | сантиньютон | сН | cN |
| 10 3 Н | килоньютон | кН | kN | 10 −3 Н | миллиньютон | мН | mN |
| 10 6 Н | меганьютон | МН | MN | 10 −6 Н | микроньютон | мкН | µN |
| 10 9 Н | гиганьютон | ГН | GN | 10 −9 Н | наноньютон | нН | nN |
| 10 12 Н | тераньютон | ТН | TN | 10 −12 Н | пиконьютон | пН | pN |
| 10 15 Н | петаньютон | ПН | PN | 10 −15 Н | фемтоньютон | фН | fN |
| 10 18 Н | эксаньютон | ЭН | EN | 10 −18 Н | аттоньютон | аН | aN |
| 10 21 Н | зеттаньютон | ЗН | ZN | 10 −21 Н | зептоньютон | зН | zN |
| 10 24 Н | иоттаньютон | ИН | YN | 10 −24 Н | иоктоньютон | иН | yN |
Интересные примеры:
Сила тяжести, действующая на человека массой 70 кг – 686 Н.
Вес тела массой 102 грамма (т. е. сила тяжести, действующая на это тело на поверхности Земли ) составляет 1 Н.
Сила, действующая на электрон со стороны ядра атома водорода, составляет 3,6967⋅10 −10 Н.
Примечание: © Фото https://www.pexels.com, https://pixabay.com
бином физика задача кольца законы формула тело сила 2 3 ньютона 9 класс работы ответ
1 ньютон физик на метр
первый второй третий закон ньютона
первого второго закона ньютона
1 2 3 закон ньютона
10 4 5 ньютонов
выразите масса в ньютонах следующие силы
чему равен ньютон
Единицы измерения силы в системе СИ. Сила в ньютонах
Каждый школьник знает, что значения всех физических величин в настоящее время представлены стандартами Международной системы единиц, или СИ. Одной из важных величин в физике является сила. Рассмотрим вопрос, какова ее единица измерения в СИ, а также в других часто используемых системах.
Что такое сила?
Прежде чем рассматривать вопрос единицы измерения силы в системе СИ, разберемся с самим понятием силы.
В классической физике под ней понимают величину, которая способна изменять характер движения некоторого объекта, например направление его движения или скорость. Эта физическая величина вместе с энергией определяет интенсивность любых взаимодействий, которые существуют в природе.

Когда говорят о силе, то принято ее рассматривать с двух точек зрения:

Примерами проявления силы в действии являются движение автомобиля (механическая сила, заставляющая вращать его колеса) или падение мяча с некоторой высоты (сила земного притяжения).
Историческая справка
Появление концепции силы относится ко временам философов Древней Греции. В частности, Архимед полагал, что любое тело пребывает в состоянии покоя, если на него не оказывают воздействие остальные тела, то есть философ рассматривал силу в статике.
Первое определение этой физической величины с динамических позиций приписывается Галилею (XVII век), который, в отличие от Архимеда, полагал, что отсутствие взаимодействия с другими объектами рассматриваемого тела не будет менять его инерционное движение.
Современную концепцию силы развил в своих трудах Исаак Ньютон. Он подробно определил это понятие, включив его во все законы классической механики. Так, Ньютон определил, что интенсивность взаимодействия абсолютно любых тел, имеющих конечную массу, уменьшается, как квадрат расстояния (закон всемирного тяготения). Только спустя один век (конец XVIII в.) Генри Кавендиш, используя крутильные весы, смог измерить гравитационную постоянную, которая была введена Ньютоном. За перечисленные заслуги Ньютона в физике, единица измерения силы в системе СИ получила название по его фамилии.
В современной физике понятие силы используется главным образом для описания макроскопических объектов. В квантовой механике и физике элементарных частиц чаще оперируют концепцией «энергия».
Международная система единиц и Ньютон
Под этим названием понимают систему мер и величин, которая кратко обозначается СИ (с франц. Système International). В ее основу положены 7 основных физических величин (ампер, кельвин, секунда, кандела, килограмм, метр и моль). СИ была принята в 1960 году, а в 1971 году в нее была добавлена последняя фундаментальная величина «моль».
Применение утвержденных в СИ приставок к основным единицам измерения позволяет получить их дробные или большие значения. Для силы это могут быть, например, мкН (микроньютон, 1 мкН = 10-6 Н), мН (миллиньютон, 1 мН = 10-3 Н) или кН (килоньютон, в ньютонах это 1000 Н).
Любопытно отметить, что ньютон не входит в число 7 фундаментальных единиц измерения силы в системе СИ, поэтому он является производной единицей. В частности, 1 [Н] = 1 [кг*м/с2], то есть он выражается через килограмм (масса), метр (расстояние) и секунду (время).
Работа силы в системе СИ
В СИ сила в ньютонах измеряется, а расстояние в метрах, поэтому работа будет выражаться в Н*м. Однако эта величина имеет собственное название: джоуль (Дж), то есть она выражается в тех же единицах, что и энергия.
Каким прибором измеряют силу?
Для измерения силы в ньютонах, килоньютонах, миллиньютонах используют прибор, который называется динамометр. Изобретен он был еще Исааком Ньютоном. Прибор представляет собой пружину, закрепленную на градуированной линейке. Поскольку растяжение пружины описывается законом Гука, то есть является упругим, то сила всегда прямо пропорциональна величине удлинения пружины. Этот факт и используется в динамометре при его градуировке.
Помимо динамометра для измерения слишком маленьких сил используют крутильные весы, основным элементом работы которых является так называемый крутильный маятник. Измерение силы с помощью этих весов основано на упругой сдвиговой деформации рабочего элемента.
Сила в других системах единиц
Система СИ используется во всем мире и во всех областях исследования, тем не менее, в некоторых сферах в виду исторических причин или простого удобства применения продолжают указываться единицы измерения из других систем. Перевод всех их в единицы СИ также стандартизированы.
Одной из популярных является система СГС (сантиметр, грамм, секунда). Эта система была предложена еще в 1832 году немецким ученым Гауссом. В ней сила измеряется в динах (дин), 1 дин эквивалентна 10-5 ньютонов. СГС часто используется для описания электромагнитных явлений, поскольку в ее форме представления многие законы выглядят проще, чем в единицах СИ.
Еще одна система единиц, которую принято называть технической, часто использовалась для описания процессов инженерии. В ней сила является фундаментальной единицей, через которую определяется масса. Называется она килограмм-силой или килопондом. Килограмм-сила представляет собой такую интенсивность воздействия на тело массой 1 кг, которая равна силе гравитационного притяжения этого тела Землей, то есть 1 килопонд = 9,81 ньютона. С появлением СИ техническая система единиц практически перестала использоваться.
чему равен 1 ньютон
Ньютон (обозначение: Н, N) — единица измерения силы в СИ.
1 ньютон равен силе, сообщающей телу массой 1 кг ускорение 1 м/с² в направлении действия силы. Таким образом, 1 Н = 1 кг·м/с².
Единица названа в честь английского физика Исаака Ньютона.
1 Н ≈ 0,101971621 кгс.
1 ньютон равен силе, сообщающей телу массой 1 кг ускорение 1 м/с² в направлении действия силы. Таким образом, 1 Н = 1 кг·м/с².
Единица названа в честь английского физика Исаака Ньютона.
1 Н ≈ 0,101971621 кгс.
У этого термина существуют и другие значения, см. Ньютон.
Ньютон (обозначение: Н, N) — единица измерения силы в СИ.
1 ньютон равен силе, сообщающей телу массой 1 кг ускорение 1 м/с² в направлении действия силы. Таким образом, 1 Н = 1 кг·м/с².
Единица названа в честь английского физика Исаака Ньютона.
Ньютон (единица измерения)
Материал из Википедии — свободной энциклопедии
У этого термина существуют и другие значения, см. Ньютон.
Ньютон (обозначение: Н, N) — единица измерения силы в СИ.
1 ньютон равен силе, сообщающей телу массой 1 кг ускорение 1 м/с² в направлении действия силы. Таким образом, 1 Н = 1 кг·м/с².
Единица названа в честь английского физика Исаака Ньютона.
1 Н ≈ 0,101971621 кгс.
Ньютон (обозначение: Н, N) — единица измерения силы в СИ.
1 ньютон равен силе, сообщающей телу массой 1 кг ускорение 1 м/с² в направлении действия силы. Таким образом, 1 Н = 1 кг·м/с².
Единица названа в честь английского физика Исаака Ньютона.
Момент силы
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Сила: что это за величина
В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или тормозит, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.
Она измеряется в Ньютонах — это единица измерения названа в честь Исаака Ньютона.
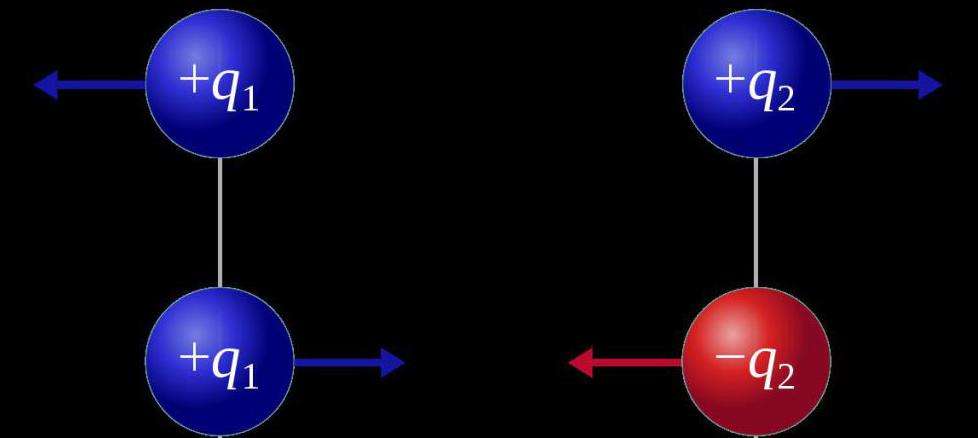
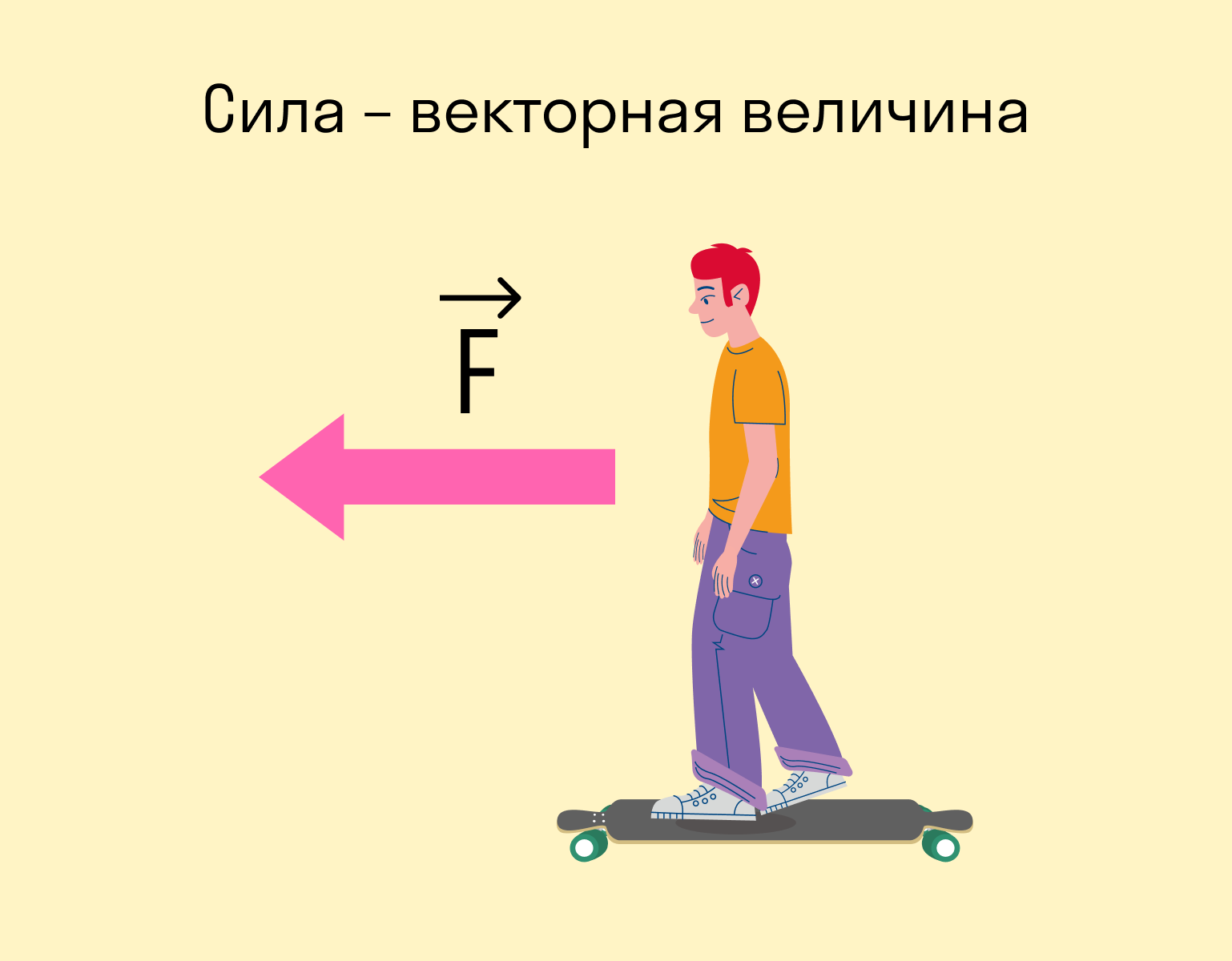
Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.
Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.
Плечо силы
Для начала давайте разберемся, что такое плечо силы — оно нам сегодня очень пригодится.
Представьте человека. Совершенно обычного. Если он совершенно обычный, у него точно будут плечи — без них получится уже какой-то инопланетянин. Если мы прочертим прямую вдоль линии плеча, а потом еще одну — вдоль линии руки — мы получим две пересекающиеся прямые. Угол между такими прямыми будет равен 90 градусов, а значит эти линии перпендикулярны.
Как анатомическое плечо перпендикулярно руке, так и в физике плечо перпендикулярно, только уже линии действия силы.
То есть перпендикуляр, проведенный от точки опоры до линии действия силы —это плечо силы.
Рычаг
В каждом дворе есть качели, для которых нужны два качающихся (если в вашем дворе таких нет, посмотрите в соседнем). Большая доска ставится посередине на точку опоры. По сути своей, качели — это рычаг.
Рычаг — простейший механизм, представляющий собой балку, вращающуюся вокруг точки опоры.
Хорошо, теперь давайте найдем плечо этой конструкции. Возьмем правую часть качелей. На качели действует сила тяжести правого качающегося, проведем перпендикуляр от линии действия силы до точки опоры. Получилась, что плечо совпадает с рычагом, разве что рычаг — это вся конструкция, а плечо — половина.
Давайте попробуем опустить качели справа, тогда что получим: рычаг остался тем же самым по длине, но вот сместился на некоторый угол, а вот плечо осталось на том же месте. Если направление действия силы не меняется, как и точка опоры, то перпендикуляр между ними невозможно изменить.
Момент силы
При решении задач на различные силы нам обычно хватало просто сил. Сила действует всегда линейно (ну в худшем случае под углом), поэтому очень удобно пользоваться законами Ньютона, приравнивать разные силы. Это работало с материальными точками, но не будет так просто применяться к телам, у которых есть форма и размер.
Вот мы приложили силу к краю палки, но при этом не можем сказать, что на другом ее конце будут то же самое ускорение и та же самая сила. Для этого мы вводим такое понятие, как момент силы.
Момент силы — это векторное произведение силы на плечо. Для определения физического смысла можно сказать, что момент — это вращательное действие.
Момент силы
M = Fl
M — момент силы [Н*м]
F — сила [Н]
l — плечо [м]
Вернемся к примеру с дверями. Вот мы приложили силу к краю двери — туда, где самый длинный рычаг. Получаем некоторое значение момента силы.
Теперь ту же силу приложим ближе к креплению двери, там, где плечо намного короче. По формуле получим момент меньшей величины.
На себе мы это ощущаем таким образом: нам легче толкать дверь там, где момент больше. То есть, чем больше момент, тем легче идет вращение.
То же самое можно сказать про гаечный ключ. Чтобы закрутить гайку, нужно взяться за ручку дальше гайки.
В этом случае, прикладывая ту же силу, мы получаем большую величину момента за счет увеличения плеча.
Расчет момента силы
Сейчас рассмотрим несколько вариантов того, как момент может рассчитываться. По идее просто нужно умножить силу на плечо, но поскольку мы имеем дело с векторами, все не так просто.
Если сила расположена перпендикулярно оси стержня, мы просто умножаем модуль силы на плечо.
Расстояние между точками A и B — 3 метра.
Момент силы относительно точки A:
Если сила расположена под углом к оси стержня, умножаем проекцию силы на плечо.
Обратите внимание, что такие задания могут встретиться только у учеников не раньше 9 класса!
Момент силы относительно точки B:
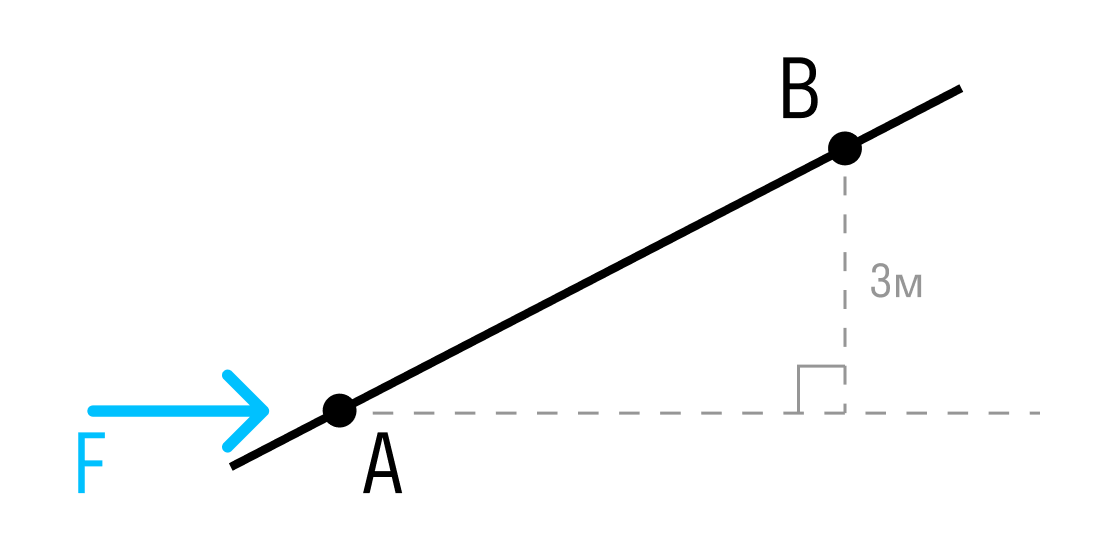
Если известно расстояние от точки до линии действия силы, момент рассчитывается как произведение силы на это расстояние (плечо).
Момент силы относительно точки B:
Правило моментов
Вернемся к нашим баранам качелям. Мы умудряемся на них качаться, потому что существует вращательное действие — момент. Силы, с которыми мы действуем на разные стороны этих качелей могут быть разными, но вот моменты должны быть одинаковыми.
Правило моментов говорит о том, что если рычаг не вращается, то сумма моментов сил, поворачивающих рычаг против часовой стрелки, равна сумме моментов сил, поворачивающих рычаг по часовой стрелке.
Это условие выполняется относительно любой точки.
Правило моментов
M1 + M2 +. + Mn = M’1 + M’2 +. + M’n
M1 + M2 +. + Mn — сумма моментов сил, поворачивающих рычаг по часовой стрелке [Н*м]
Давайте рассмотрим этот закон на примере задач.
Задача 1
К левому концу невесомого стержня прикреплен груз массой 3 кг.
Стержень расположили на опоре, отстоящей от его левого конца на 0,2 длины стержня. Чему равна масса груза, который надо подвесить к правому концу стержня, чтобы он находился в равновесии?
Решение:
Одним из условий равновесия стержня является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно точки опоры. Момент, создаваемый левым грузом равен mgL5 он вращает стержень против часовой стрелки. Момент, создаваемый правым грузом:Mg4L5 — он вращает по часовой.
Приравнивая моменты, получаем, что для равновесия к правому концу стержня необходимо подвесить груз массой
M = m : 4 = 3 : 4 = 0,75 кг
Ответ: для равновесия к правому концу стержня необходимо подвесить груз массой 0,75 кг
Задача 2
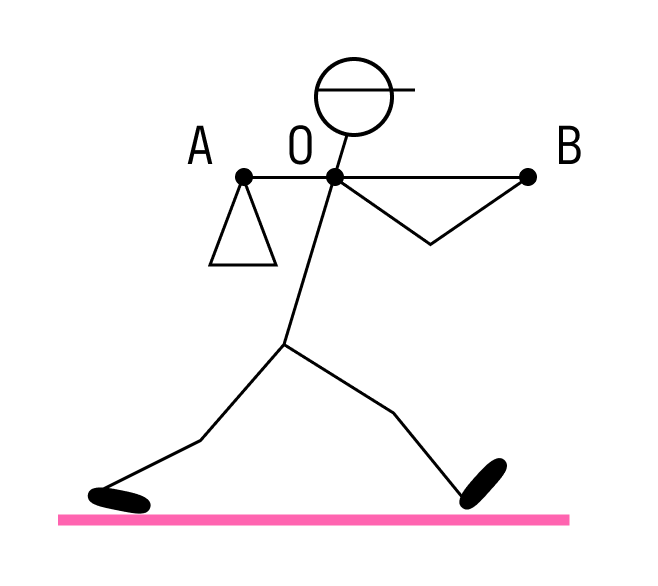
Путешественник несёт мешок с вещами на лёгкой палке. Чтобы удержать в равновесии груз весом 80 Н, он прикладывает к концу B палки вертикальную силу 30 Н. OB = 80 см. Чему равно OA?
Решение:
По правилу рычага: FB/FA=|OA|/|OB| где FA и FB — силы, приложенные соответственно к точкам A и B. Выразим длину OA:
Ответ: расстояние ОА равно 30 см
Задача 3
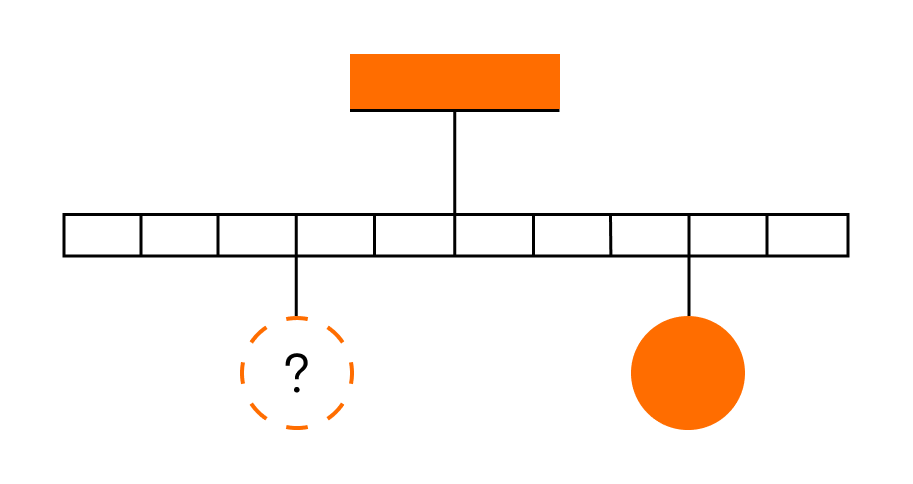
Тело массой 0,2 кг подвешено к правому плечу невесомого рычага (см. рисунок). Груз какой массы надо подвесить ко второму делению левого плеча рычага для достижения равновесия?
Решение:
По правилу рычага m1g*l1=m2g*l2
Отсюда m2=l1/l2*m1=3/2*0,2 = 0,3 кг
Ответ: Масса груза равна 0,3 кг
Задача 4
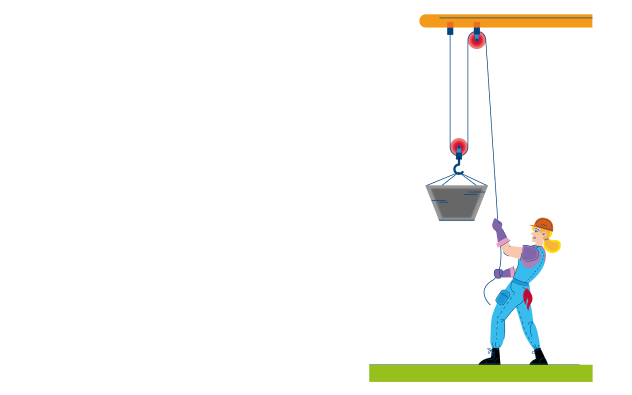
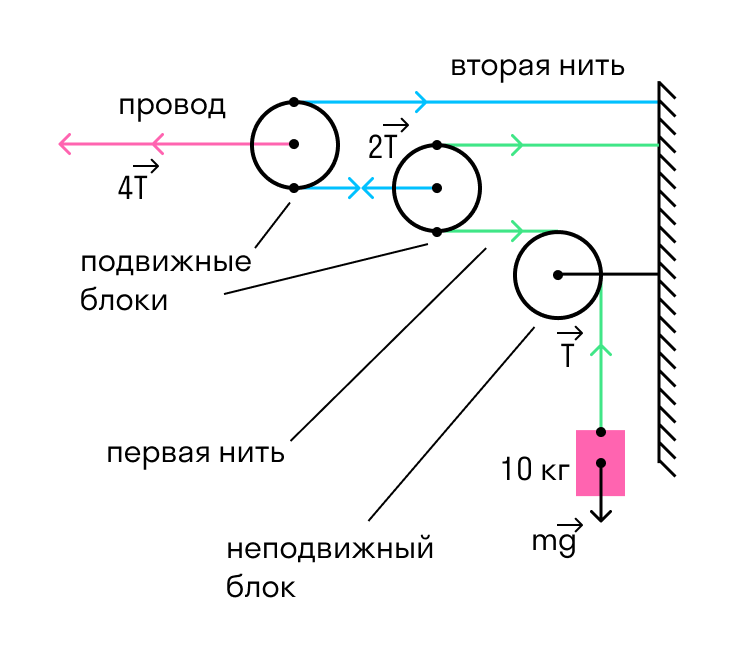
На железной дороге для натяжения проводов используется показанная на рисунке система, состоящая из легких блоков и тросов, натягиваемых тяжелым грузом. Чему равна сила натяжения провода?
Решение:
Система на рисунке состоит из трех блоков: двух подвижных и одного неподвижного. Назначение неподвижного блока заключается только в том, что он меняет направление действия силы, однако никакого выигрыша в силе при этом не возникает. Каждый подвижный блок, напротив, дает выигрыш в силе.
Определим силу, с которой натянута первая нить. Груз растягивает ее с силой:
T = mg = 10*10 = 100 Н
Рассмотрим теперь первый подвижный блок. Так как вся система статична, полная сила, действующая на этот блок, должна быть равна нулю. Первая нить тянет его направо с суммарной силой 2T, значит, натяжение второй нити тоже должно быть равно 2T (вот он — выигрыш в силе). Аналогичное рассмотрение для второго подвижного блока показывает, что натяжение провода должно быть равно
Ответ: натяжение провода равно 400 Н
Задача 5 — a.k.a самая сложная задачка
Под действием силы тяжести mg груза и силы F рычаг, представленный на рисунке, находится в равновесии. Вектор силы F перпендикулярен рычагу, груз на плоскость не давит. Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную и горизонтальную оси указаны на рисунке.
Если модуль силы F равен 120 Н, то каков модуль силы тяжести, действующей на груз?
Решение:
Одним из условий равновесия рычага является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно опоры рычага. Момент, создаваемый силой F, равен F*5 м и он вращает рычаг по часовой стрелке. Момент, создаваемый грузом относительно этой точки — mg*0,8 м, он вращает против часовой. Приравнивая моменты, получаем выражение для модуля силы тяжести
Ответ: модуль силы тяжести, действующей на груз равен 750 Н