второй закон ньютона в импульсной форме определение и формула
Как выводится и формулируется второй закон Ньютона в импульсной форме
Второй постулат динамики записывают несколькими способами, например, используя импульс. Указанная формулировка встречается гораздо реже обычного, однако решает ряд задач школьной, университетской механики.
Второй закон Ньютона в импульсной форме
В общем случае запись главного постулата динамики включает три составляющие:
Второй закон Ньютона в импульсной форме записывают, определив изначально импульс тела – величину, получаемую вследствие умножения массы на скорость движения:
Измеряется результатом деления произведения килограмма, метра на секунду –
Очевидно: описываемая мера механического движения — величина векторная, совпадающая с направлением
Физика использует понятие импульса силы – величины, равной результату произведения существующего воздействия, времени:
Измеряется произведением ньютона, секунды –
Импульс действующей силы равен изменению импульса объекта.
Изменение импульса во времени равно величине действующей силы.
Второй закон ньютона в импульсной форме формула
Самостоятельно выразим требующуюся формулу, используя известную запись:
Определение ускорение гласит: данная величина характеризует увеличение, уменьшение скорости:
– приобретённая, начальная скорости,
– изменение времени.
Зная стандартный вид постулата, выразим ускорение, приравняем к полученному выражению:
Части уравнения умножим на , получим:
Правая часть уравнения равна , преобразуем равенство, получим:
Глядя на получившуюся формулу сформулируем второй закон Ньютона через импульс.
Изменение импульса тела равно импульсу действовавшей на тело силы.
Формулировка аксиомы ньютоновской динамики, использующая понятие импульса, полностью соответствует виду, изначально выведенному учёным. Получить подобную запись возможно, учитывая оператор, называемый дифференциалом. Дифференциал функции d – приращение, изменение.
Формула a записывается видом:
Читается: «изменение скорости при изменяющемся времени».
Приравнивая правые части, получаем:
Умножаем части уравнения на m, сразу вносим массу под знак дифференциала:
В каких случаях применяют импульсную форму
Некоторые задачи невозможно решить, применяя обычную формулу постулата динамики. Например, задания движения тела изменяющегося веса.
Русский механик, учёный Иван Всеволод Мещерский на основе импульсной формы вывел уравнение, позволяющее решать задачи перемещения объектов переменной массы. Уравнением Мещерского удобно выводить формулу Константина Эдуардовича Циолковского, использующуюся при проектировании баллистических, космических ракет. Указанные летательные аппараты — реальный пример тел, изменяющих вес.
Более приземлённые, обыденные задачи применения описываемой записи 2 постулата – движение двух сталкивающихся шаров, движение одного шара, ударяющегося о препятствие.
Пример использования
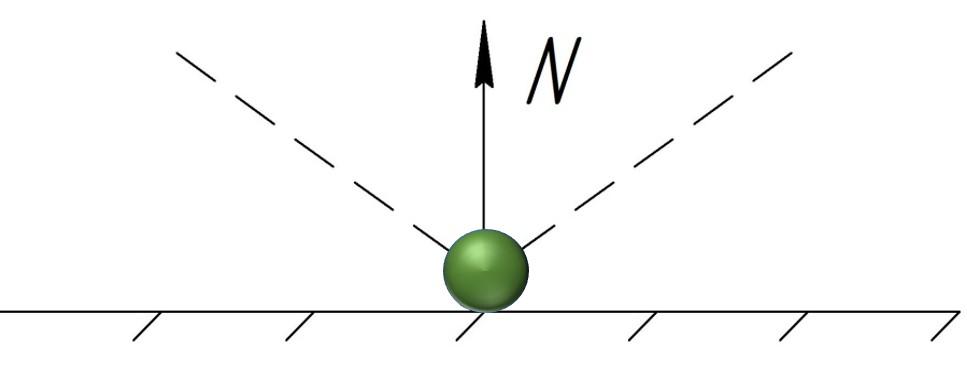
Пусть шарик, обладающий массой m, неизменяющейся скоростью , ударяется о стену под углом
, спустя
отлетает.
Принимаем допущение: стена гладкая, трение отсутствует. Шарик, ударяясь, испытывает воздействие силы упругости N.
Сила, действующая на тело, является единственной, видоизменим запись:
Найдём , используя правило сложения векторов – векторный треугольник.
Потери скорости отсутствуют, вес остаётся прежним, следовательно, . Получившийся векторный треугольник равнобедренный. Неизвестный вектор:
Второй закон Ньютона в импульсной форме позволяет решать задачи разного уровня значимости: школьные типовые задания, проекты космического масштаба.
Второй закон Ньютона в импульсной форме
Любое тело, обладающее скоростью, обладает импульсом.
Скорость тела будет меняться, когда на него подействует сила и появится ускорение. Об этом сообщает второй закон Ньютона. А если изменяется скорость тела, то будет изменяться его импульс.
Второй закон Ньютона в импульсной форме описывает изменение импульса тела под действием силы.
Формула второго закона Ньютона в импульсной форме
Импульсная форма записи второго закона выглядит так:
Словами это выражение можно сформулировать так:
\(\overrightarrow <\Delta p>\left( \text <кг>\cdot \frac<\text<м>>
\( \overrightarrow < F \cdot \Delta t>\left( H \cdot \text <м>\right) \) – вектор импульса силы;
Слева и справа в формуле находятся два вектора. Так как между ними записан знак равенства, значит у векторов \(\overrightarrow <\Delta p>\) и \( \overrightarrow < F \cdot \Delta t>\) совпадают обе характеристики — направление и длина.
С помощью математики фразу «длины векторов равны» можно записать так:
\( \left| \overrightarrow <\Delta p>\right | = \left| \overrightarrow < F \cdot \Delta t>\right | \)
Как посчитать длину вектора, и как ее обозначать, читайте тут.
Пояснения и вывод формулы с помощью геометрии
Чтобы получить импульсный вид записи для второго закона, рассмотрим такую задачу.
Представим, что мы склонились над бильярдным столом и смотрим на него сверху. А в это время по столу катится бильярдный шар с какой-то постоянной скоростью.
Примечание: с постоянной скоростью, значит — с одной и той же скоростью. О такой скорости физики часто говорят «с неизменной скоростью», а математики применяют для нее запись \( \vec
Пусть для определенности масса шара равна двум килограммам.
\( m = 2 \left( \text <кг>\right) \)
Пусть до того, как мы подействовали на шар, он двигался по столу в направлении, указанном на рисунке 1а. Шар вначале движется по горизонтали (рис. 1а), вектор начальной скорости обозначен \( \vec
После удара шар будет катиться уже не по горизонтали на рисунке. Физики скажут: направление движения шара изменилось. Направление, в котором шар движется после удара, обозначено вектором \( \vec
Нам известны начальная и конечная скорости тела, а также, его масса. Мы можем вычислить импульс тела до удара (рис 2а), и после удара (рис 2б).
\( m \cdot \vec
\( m \cdot \vec
\) – импульс тела после удара (конечный).
Обратите внимание, что у векторов начального импульса \( \vec
\), так же, сонаправлен с вектором \( \vec
Для удобства совместим начала векторов \( \vec
\) (рис. 3). Зададимся вопросом, как из вектора начального импульса \( \vec
\) вектор?
Очевидно, нужно к вектору \( \vec
Подробнее о том, как складывать векторы, написано тут.
Сумму можно записать так:
Это уравнение записано в векторном виде. Стрелки над символами подчеркивают тот факт, что векторы складывают с помощью геометрии, то есть, учитывают их направления.
Выразим теперь вектор, обозначенный \( \overrightarrow <\Delta p>\). Для этого, из обеих частей уравнения вычтем вектор \( \vec
Видно, что вектор \( \overrightarrow <\Delta p>\) – это разница между конечным \( \vec
\) и начальным \( \vec
Физики для вектора \( \overrightarrow <\Delta p>\) используют такое название:
\( \overrightarrow <\Delta p>\left( \text <кг>\cdot \frac<\text<м>>
Рассмотрим теперь совместно векторы \( \overrightarrow <\Delta p>\) и \( \vec
Направления векторов совпадают, а длина – различается.
Примечание: Математики вместо выражения «длина вектора» употребляют термин «модуль вектора».
Предположим, у нас есть точный хронометр и мы измерили кусочек времени, в течение которого сила действовала на бильярдный шар.
Умножим теперь вектор \( \vec
Из рисунка 6 видно, что у векторов \(\overrightarrow <\Delta p>\) и \( \overrightarrow < F \cdot \Delta t>\) совпадают не только направления, но и длины.
Если у векторов совпадают обе характеристики, то их можно приравнять. Подробнее о том, какие у векторов есть характеристики, написано тут.
Это выражение называют вторым законом Ньютона, записанным в импульсной форме.
Примечания
1). Сумму векторов
можно теперь переписать в таком виде:
2). Складывать можно векторы, у которых размерность совпадает.
О сложении векторов простым языком написано тут.
Обратим внимание на размерность.
\( \overrightarrow < F \cdot \Delta t>\left( H \cdot c \right) \)
На первый взгляд, она отличается, но с помощью простых преобразований можно показать, что
\[ \large 1 \text <кг>\cdot \frac< 1\text<м>> <1 c>= 1 H \cdot 1 c \]
Вывод формулы с помощью алгебры
Второй закон Ньютона в импульсной форме можно получить из алгебраических соображений.
Пусть для определенности векторы скоростей тела и вектор силы направлены вдоль одной прямой линии, т. е. движение прямолинейное.
Применим выражение для ускорения
Полученное выражение является пропорцией. Применив одно из свойств пропорции, получим такое выражение:
В правой части находится вектор \(\overrightarrow <\Delta v>= \vec
Преобразуем правую часть
\(\overrightarrow<\Delta v>\cdot m = \left( \vec
Раскрыв скобки, получим
\(\overrightarrow<\Delta v>\cdot m = \vec
Подставляя их, получим
\(\overrightarrow<\Delta v>\cdot m = \overrightarrow<\Delta p>\)
То есть, вектор \(\overrightarrow <\Delta v\cdot m>\) – это вектор \(\overrightarrow <\Delta p>\).
Тогда второй закон Ньютона в импульсной форме запишем так
Закон cохранения импульса
9 класс, 10 класс, ЕГЭ/ОГЭ
Импульс: что это такое
Как-то раз Рене Декарт (это который придумал ту самую декартову систему координат) решил, что каждый раз считать силу, чтобы описать процессы — как-то лень и сложно.
Для этого нужно ускорение, а оно не всегда очевидно. Тогда он придумал такую величину, как импульс. Импульс можно охарактеризовать, как количество движения — это произведение массы на скорость.
Импульс тела
→ →
p = mv
p — импульс тела [кг*м/с]
Закон сохранения импульса
В физике и правда ничего не исчезает и не появляется из ниоткуда. Импульс — не исключение. В замкнутой изолированной системе (это та, в которой тела взаимодействуют только друг с другом) закон сохранения импульса звучит так:
Закон сохранения импульса
Векторная сумма импульсов тел в замкнутой системе постоянна
А выглядит — вот так:
Закон сохранения импульса
→ → →
p1 + p2 + … + pn = const
p — импульс тела [кг*м/с]
Простая задачка
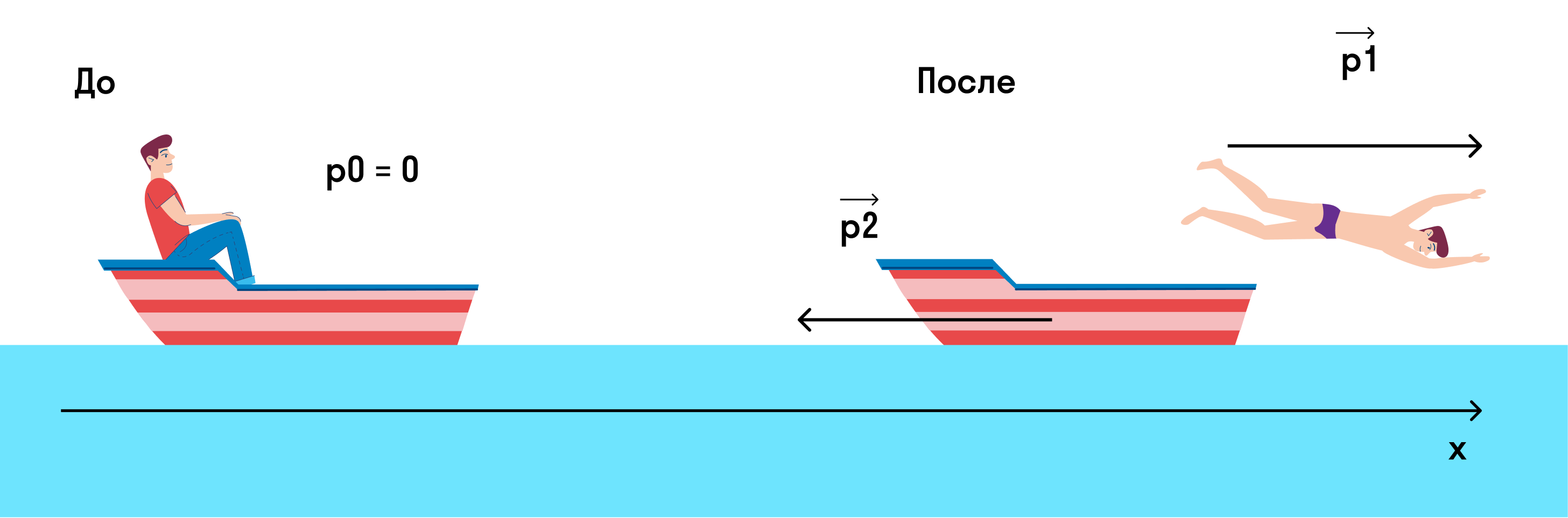
Мальчик массой m = 45 кг плыл на лодке массой M = 270 кг в озере и решил искупаться. Остановил лодку (совсем остановил, чтобы она не двигалась) и спрыгнул с нее с горизонтально направленной скоростью 3 м/с. С какой скоростью станет двигаться лодка?
Решение:
Запишем закон сохранения импульса для данного процесса.
p0 — это импульс системы мальчик + лодка до того, как мальчик спрыгнул,
p1 — это импульс мальчика после прыжка,
p2 — это импульс лодки после прыжка.
Изобразим на рисунке, что происходило до и после прыжка.
Если мы спроецируем импульсы на ось х, то закон сохранения импульса примет вид
0 = p1 — p2
p1 = p2
Подставим формулу импульса.
mV1 = MV2
Выразим скорость лодки V2:
V2 = mV1/M
Подставим значения:
V2 = 45*3/270 = 3/6 = ½ = 0,5 м/с
Ответ: скорость лодки после прыжка равна 0,5 м/с
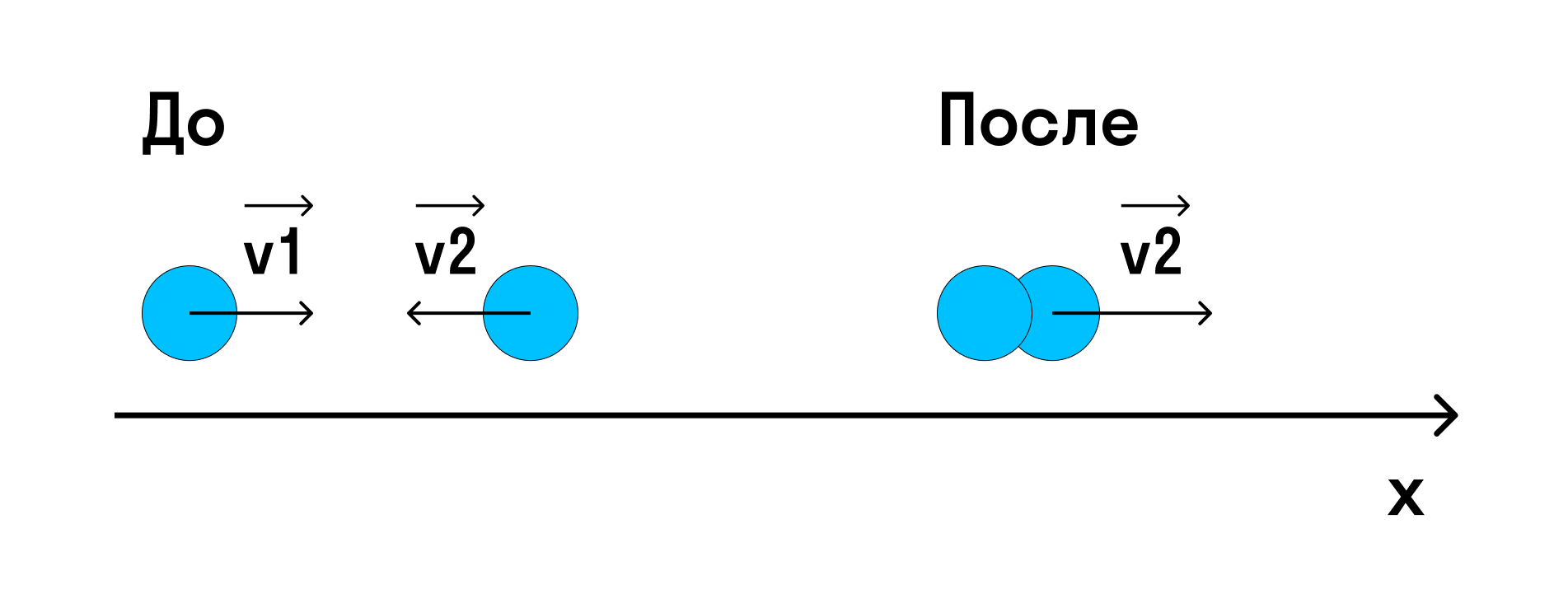
Задачка посложнее
Решение: Для данной системы выполняется закон сохранения импульса:
Импульс системы до удара — это сумма импульсов тел, а после удара — импульс «получившегося» в результате удара тела.
Спроецируем импульсы на ось х:
После неупругого удара получилось одно тело массы m1 + m2, которое движется с искомой скоростью:
m1v1 — mv2 = (m1 + m2) v
Отсюда находим скорость тела, образовавшегося после удара:
v = (m1v1 — mv2)/(m1 + m2)
Переводим массу в килограммы и подставляем значения:
В результате мы получили отрицательное значение скорости. Это значит, что в самом начале на рисунке мы направили скорость после удара неправильно.
Знак минус указывает на то, что слипшиеся тела двигаются в сторону, противоположную оси X. Это никак не влияет на значение получившееся значение.
Ответ: скорость системы тел после соударения равна v = 0,2 м/с.
Второй закон Ньютона в импульсной форме
Второй закон Ньютона в импульсной форме можно получить следующим образом. Пусть для определенности векторы скоростей тела и вектор силы направлены вдоль одной прямой линии, т. е. движение прямолинейное.
Запишем второй закон Ньютона, спроецированный на ось х, сонаправленную с направлением движения и ускорением:
Применим выражение для ускорения
Полученное выражение является пропорцией. Применив основное свойство пропорции, получим такое выражение:
В правой части находится Δv =v —v0 — это разница между конечной и начальной скоростью.
Преобразуем правую часть
Раскрыв скобки, получим
Заменим произведение массы и скорости на импульс:
То есть, вектор Δv⋅m – это вектор Δp.
Тогда второй закон Ньютона в импульсной форме запишем так
Вернемся к векторной форме, чтобы данное выражение было справедливо для любого направления вектора ускорения.
Задачка про белку отлично описывает смысл второго закона Ньютона в импульсной форме
Белка с полными лапками орехов сидит на гладком горизонтальном столе. И вот кто-то бесцеремонно толкает ее к краю стола. Белка понимает законы Ньютона и предотвращает падение. Но как?
Решение:
Чтобы к белке приложить силу, которая будет толкать белку в обратном направлении от края стола, нужно создать соответствующий импульс (вот и второй закон Ньютона в импульсной форме подъехал).
Ну, а чтобы создать импульс, белка может выкинуть орехи в сторону направления движения — тогда по закону сохранения импульса ее собственный импульс будет направлен против направления скорости орехов.
Реактивное движение
В основе движения ракет, салютов и некоторых живых существ: кальмаров, осьминогов, каракатиц и медуз — лежит закон сохранения импульса. В этих случаях движение тела возникает из-за отделения какой-либо его части. Такое движение называется реактивным.
Яркий пример реактивного движения в технике — движение ракеты, когда из нее истекает струя горючего газа, которая образуется при сгорании топлива.
Сила, с которой ракета действует на газы, равна по модулю и противоположна по направлению силе, с которой газы отталкивают от себя ракету:
Сила F2 называется реактивной. Это та сила, которая возникает в процессе отделения части тела. Особенностью реактивной силы является то, что она возникает без взаимодействия с внешними телами.
Закон сохранения импульса позволяет оценить скорость ракеты.
mг vг = mр vр,
где mг — это масса горючего,
vг — скорость горючего,
vр — скорость ракеты.
Отсюда можно выразить скорость ракеты:
Скорость ракеты при реактивном движении
vр = mг vг / mр
mг — это масса горючего [кг]
vг — скорость горючего [м/с]
mр — масса ракеты [кг]
v р — скорость ракеты [м/с]
Эта формула справедлива для случая мгновенного сгорания топлива. Мгновенное сгорание — это теоретическая модель. В реальной жизни топливо сгорает постепенно, так как мгновенное сгорание приводит к взрыву.
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
Записаться на марафон
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
Физика. 10 класс
Импульс тела и импульс силы
Импульс. Закон сохранения импульса
Необходимо запомнить
Импульс тела равен сумме импульсов отдельных элементов.
Импульс системы тел равен векторной сумме импульсов каждого из тел системы:
Силы, с которыми взаимодействуют между собой тела системы, называют внутренними, а силы, создаваемые телами, не принадлежащими к данной системе, – внешними.
Систему, на которую не действуют внешние силы, или векторная сумма внешних сил равна нулю, называют замкнутой.
Абсолютно неупругий удар – столкновение тел, в результате которого они соединяются вместе и движутся дальше как одно целое.
Абсолютно упругий удар – столкновение тел, в результате которого не происходит соединения тел в одно целое и их внутренние энергии остаются неизменными.
Закон сохранения импульса:
Решение задачи на применение закона сохранения импульса
Количество движения
Французский учёный Рене Декарт попытался импульс использовать как величину, заменяющую силу. Потому что силу измерять достаточно сложно, а измерить массу и скорость несложно. Поэтому часто говорят, что импульс – это количество движения (именно Ньютон впервые назвал количеством движения произведение массы тела на скорость).
Декарт, судя по его высказываниям, понимал фундаментальное значение введенного им в XVII веке понятия количества движения – или импульса тела – как произведения массы тела на величину его скорости. И хотя он совершил ошибку, не рассматривая количество движения как векторную величину, сформулированный им закон сохранения количества движения выдержал с честью проверку временем. Ошибка была исправлена в начале XVIII века, и триумфальное шествие этого закона в науке и технике продолжается по сию пору.
. Декарт обосновывал принцип сохранения количества движения совершенством бога, «действующего с величайшим постоянством и неизменностью».
. закон сохранения импульса позволяет «разыскать» и невидимые объекты, например, электромагнитные волны, излучаемые открытым колебательным контуром, или антинейтрино – субатомные частицы, не оставляющие следов в детекторах.
Импульс
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: импульс тела, импульс системы тел, закон сохранения импульса.
Импульс тела — это векторная величина, равная произведению массы тела на его скорость:
Специальных единиц измерения импульса нет. Размерность импульса — это просто произведение размерности массы на размерность скорости:
Почему понятие импульса является интересным? Оказывается, с его помощью можно придать второму закону Ньютона несколько иную, также чрезвычайно полезную форму.
Второй закон Ньютона в импульсной форме
С учётом того, что ускорение тела равно производной вектора скорости, второй закон Ньютона переписывается следующим образом:
Вносим константу под знак производной:
Как видим, в левой части получилась производная импульса:
Соотношение ( 1 ) и есть новая форма записи второго закона Ньютона.
Второй закон Ньютона в импульсной форме. Производная импульса тела есть равнодействующая приложенных к телу сил.
Можно сказать и так: результирующая сила, действующая на тело, равна скорости изменения импульса тела.
Производную в формуле ( 1 ) можно заменить на отношение конечных приращений:
В задачах, как правило, интервал времени достаточно мал. Например, это может быть время соударения мяча со стенкой, и тогда — средняя сила, действующая на мяч со стороны стенки во время удара.
Подчеркнём ещё раз, что изменение импульса — это разность векторов (рис. 1 ):
 |
| Рис. 1. Изменение импульса |
Пусть, например, мяч летит перпендикулярно стенке (импульс перед ударом равен ) и отскакивает назад без потери скорости (импульс после удара равен ). Несмотря на то, что импульс по модулю не изменился ( ), изменение импульса имеется:
Геометрически эта ситуация показана на рис. 2 :
 |
| Рис. 2. Изменение импульса при отскоке назад |
Перепишем формулу ( 2 ) следующим образом:
или, расписывая изменение импульса, как и выше:
Величина называется импульсом силы. Специальной единицы измерения для импульса силы нет; размерность импульса силы равна просто произведению размерностей силы и времени:
(Обратите внимание, что оказывается ещё одной возможной единицей измерения импульса тела.)
Словесная формулировка равенства ( 3 ) такова: изменение импульса тела равно импульсу действующей на тело силы за данный промежуток времени. Это, разумеется, снова есть второй закон Ньютона в импульсной форме.
Пример вычисления силы
В качестве примера применения второго закона Ньютона в импульсной форме давайте рассмотрим следующую задачу.
Решение. Покажем прежде всего, что угол отражения равен углу падения, то есть шарик отскочит от стены под тем же углом (рис. 3 ).
 |
| Рис. 3. К задаче (вид сверху) |
Тут всё дело в том, что стена — гладкая. Это значит, что трения между шариком и стеной нет. Следовательно, со стороны стены на шарик действует единственная сила — сила упругости, направленная перпендикулярно стене (рис. 4 ).
 |
| Рис. 4. К задаче |
 |
| Рис. 5. К задаче |
Теперь заметим вдобавок, что в нашем равнобедренном треугольнике есть угол (это угол падения); стало быть, данный треугольник — равносторонний. Отсюда:
И тогда искомая средняя сила, действующая на шарик:
Импульс системы тел
Начнём с простой ситуации системы двух тел. А именно, пусть имеются тело 1 и тело 2 с импульсами и соответственно. Импульс системы данных тел — это векторная сумма импульсов каждого тела:
Оказывается, для импульса системы тел имеется формула, аналогичная второму закону Ньютона в виде ( 1 ). Давайте выведем эту формулу.
Все остальные объекты, с которыми взаимодействуют рассматриваемые нами тела 1 и 2, мы будем называть внешними телами. Силы, с которыми внешние тела действуют на тела 1 и 2, называем внешними силами. Пусть — результирующая внешняя сила, действующая на тело 1. Аналогично — результирующая внешняя сила, действующая на тело 2 (рис. 6 ).
 |
| Рис. 6. Система двух тел |
Запишем для каждого тела 1 и 2 второй закон Ньютона в форме ( 1 ):
Сложим равенства ( 4 ) и ( 5 ):
Но — это импульс системы тел 1 и 2. Обозначим также — это результирующая внешних сил, действующих на систему. Получаем:
Таким образом, скорость изменения импульса системы тел есть равнодействующая внешних сил, приложенных к системе. Равенство ( 6 ), играющее роль второго закона Ньютона для системы тел, мы и хотели получить.
Формула ( 6 ) была выведена для случая двух тел. Теперь обобщим наши рассуждения на случай произвольного количества тел в системе.
Импульсом системы тел тел называется векторная сумма импульсов всех тел, входящих в систему. Если система состоит из тел, то импульс этой системы равен:
Дальше всё делается совершенно так же, как и выше (только технически это выглядит несколько сложнее). Если для каждого тела записать равенства, аналогичные ( 4 ) и ( 5 ), а затем все эти равенства сложить, то в левой части мы снова получим производную импульса системы, а в правой части останется лишь сумма внешних сил (внутренние силы, попарно складываясь, дадут нуль ввиду третьего закона Ньютона). Поэтому равенство ( 6 ) останется справедливым и в общем случае.
Закон сохранения импульса
Система тел называется замкнутой, если действия внешних тел на тела данной системы или пренебрежимо малы, или компенсируют друг друга. Таким образом, в случае замкнутой системы тел существенно лишь взаимодействие этих тел друг с другом, но не с какими-либо другими телами.
Но если производная вектора обращается в нуль (скорость изменения вектора равна нулю), то сам вектор не меняется со временем:
Закон сохранения импульса. Импульс замкнутой системы тел остаётся постоянным с течением времени при любых взаимодействиях тел внутри данной системы.
Простейшие задачи на закон сохранения импульса решаются по стандартной схеме, которую мы сейчас покажем.
 |
| Рис. 7. К задаче |
Поскольку поверхность гладкая, трения нет. Поскольку поверхность горизонтальная, а движение происходит вдоль неё, сила тяжести и реакция опоры уравновешивают друг друга:
Таким образом, векторная сумма сил, приложенных к системе данных тел, равна нулю. Это значит, что система тел замкнута. Стало быть, для неё выполняется закон сохранения импульса:
Импульс системы до удара — это сумма импульсов тел:
Из закона сохранения импульса ( 7 ) имеем:
Отсюда находим скорость тела, образовавшегося после удара:
Переходим к проекциям на ось :
По условию имеем: м/с, м/с, так что
Закон сохранения проекции импульса
Покажем это более строго. Спроектируем равенство ( 6 ) на ось :
Следовательно, проекция есть константа:
Закон сохранения проекции импульса. Если проекция на ось суммы внешних сил, действующих на систему, равна нулю, то проекция импульса системы не меняется с течением времени.
Давайте посмотрим на примере конкретной задачи, как работает закон сохранения проекции импульса.
 |
| Рис. 8. К задаче |
Импульс системы «мальчик + камень» не сохраняется. Это видно хотя бы из того, что после броска появляется вертикальная составляющая импульса системы (а именно, вертикальная составляющая импульса камня), которой до броска не было.