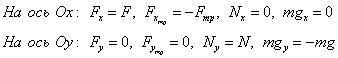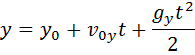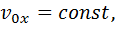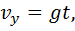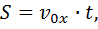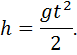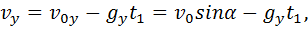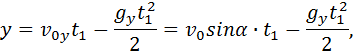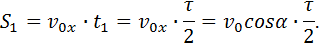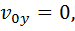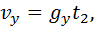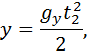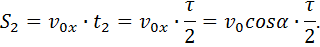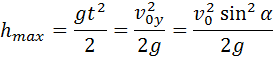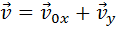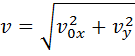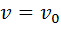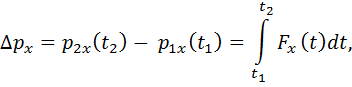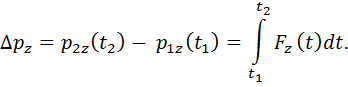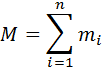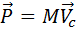второй закон ньютона в дифференциальной форме

Второй закон ньютона в дифференциальной форме

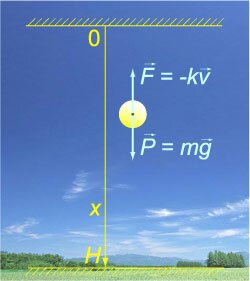
Второй закон Ньютона устанавливает связь между силой \(\mathbf,\) действующей на тело массы \(m,\) и ускорением \(\mathbf,\) которое приобретает тело под действием этой силы.

Последующее интегрирование функции \(\) позволяет найти закон движения тела \(.\) К сожалению, это не всегда можно сделать аналитически из-за громоздкости выражения для \(.\)

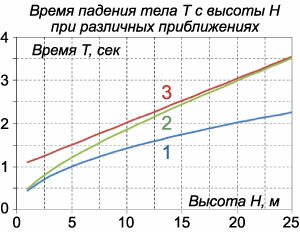
падение тела в поле тяжести без учета сопротивления воздуха (синяя кривая \(1\)). В этом случае зависимость \(T\left( H \right)\) определяется формулой \(T = \sqrt <\large\frac<<2H>>\normalsize> ;\)

точное решение нелинейного алгебраического уравнения для \(T\) (зеленая кривая \(2\)).

Из этих графиков видно, что сила сопротивления воздуха практически компенсирует силу тяжести уже через несколько секунд после начала падения. После этого движение тела происходит равномерно. Поэтому при падении с большой высоты (в данном примере это более \(20\;\text<м>\)) для оценки времени падения вполне можно использовать приближенную формулу \(T\left( H \right).\)

силой тяжести \(P = \large\frac<>\normalsize,\) где \(x\) − длина части цепочки, свисающей со стола, \(m\) − масса цепочки, \(L\) − ее длина, \(g\) − ускорение свободного падения;

Источник

Второй закон ньютона в дифференциальной форме

Приступая к формулировке второго закона, следует вспомнить, что в динамике вводятся две новые физические величины – масса тела m и сила 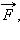а также способы их измерения. Первая из этих величин – масса – является количественной характеристикой инертных свойств тела. Она показывает, как тело реагирует на внешнее воздействие.

Вторая – сила 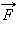– является количественной мерой действия одного тела на другое.

В качестве примера рассмотрим данный рисунокс велосипедистом. Велосипедист наклоняется в сторону поворота. Сила тяжести и сила реакции опоры со стороны земли дают равнодействующую силу, сообщающую центростремительное ускорение, необходимое для движения по окружности

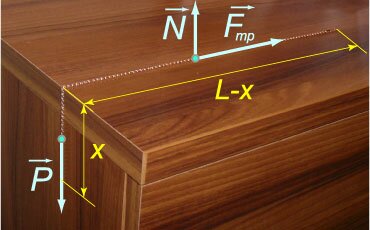
Более подробно о записи уравнений. Если в некотором направлении тело двигается равномерно или покоится, то алгебраическая сумма (с учетом знаков) проекций сил равна нулю. Если в некотором направлении тело движется равноускоренно, то алгебраическая сумма проекций сил равна произведению массы на ускорение, согласно второму закону Ньютона.

Лебедь, Щука и Рак

Для начала о бозначим силы, выберем координатные оси.

2)Тело, которое прижимают к вертикальной стенке, равноускоренно движется вниз. На тело действуют сила тяжести, сила трения, реакция опоры и сила, с которой прижимают тело. Вектор ускорения направлен вертикально вниз. Равнодействующая сила направлена вертикально вниз.

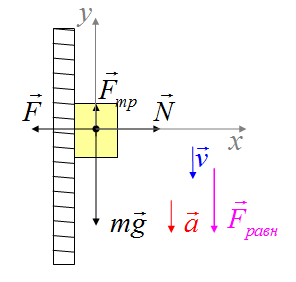
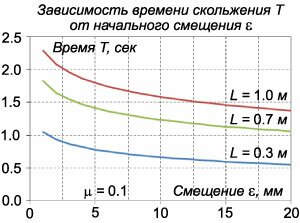
3)Тело равноускоренно движется по клину, наклон которого альфа. На тело действуют сила тяжести, сила реакции опоры, сила трения.

Главное запомнить

1) Если тело покоится или движется равномерно, то равнодействующая сила равна нулю и ускорение равно нулю;
2) Если тело движется равноускоренно, значит равнодействующая сила не нулевая;
3) Направление вектора равнодействующей силы всегда совпадает с направлением ускорения;
4) Уметь записывать уравнения проекций действующих на тело сил

Второй закон Ньютона – это фундаментальный закон природы; он является обобщением опытных фактов, которые можно разделить на две категории:

Если на тела разной массы подействовать одинаковой силой, то ускорения, приобретаемые телами, оказываются обратно пропорциональны массам:

при F = const.

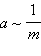
Если силами разной величины подействовать на одно и то же тело, то ускорения тела оказываются прямо пропорциональными приложенным силам:

при m = const.

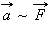
Если равнодействующая сила 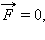то тело будет оставаться в состоянии покоя или равномерного прямолинейного движения. Таким образом, формально второй закон Ньютона включает как частный случай первый закон Ньютона, однако первый закон Ньютона имеет более глубокое физическое содержание – он постулирует существование инерциальных систем отсчета.

Особенностии второго закона Ньютона:

Источник

Второй закон Ньютона.

Второй закон Ньютона формулируется следующим образом:

Ускорение тела прямо пропорционально равнодействующей всех сил, приложенных к телу, и обратно пропорционально его массе.

.

Действующие на тело силы определяют его ускорение, поэтому направление ускорения всегда совпадает с направлением действующей силы.

Скалярно второй закон Ньютона выражается в виде:

.

Отсюда можно сделать два вывода:

1. Чем больше приложенная к телу сила, тем больше его ускорение, и тем быстрее изменяется скорость его движения.

2. Чем больше масса тела, тем меньше его ускорение в результате действия этой силы и тем медленнее оно изменяет свою скорость.

Связь между силой и ускорением тела можно установить с помощью опыта. Сначала с помощью растянутой пружины подействуем на тележку и вычислим модуль а ускорения по пройденному за время t пути s₁. Ту же самую пружину прикрепим к двум таким тележкам, т. е. используем в два раза больщую массу. Тележки за то же время t пройдут вдвое меньший путь s₂, т. е. они движутся с вдвое меньшим ускорением.

Это значит, что при действии одной и той же силы на разные тела произведение массы на ускорение одинаково: F = ma.

Необходимо помнить, что во втором законе Ньютона, как и в первом законе Ньютона, под телом подразумевают материальную точку, движение которой рассматривают в инерциальной системе отсчета.

Источник

ДИНАМИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ

Свободное падение тел

Падение тела – равноускоренное движение.

Движение тела вверх –равнозамедленное движение.

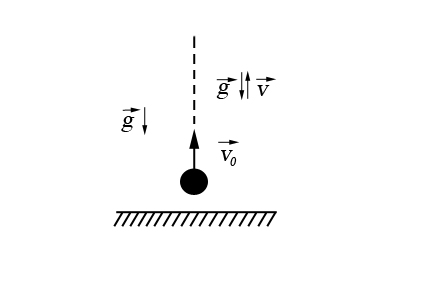Уравнения движения тела при свободном падении:

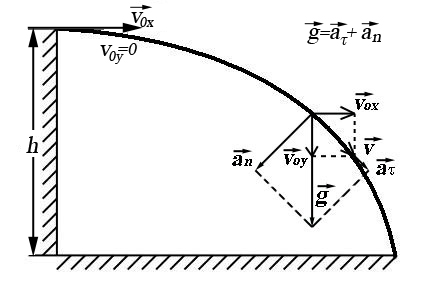
Движение тела, брошенного горизонтально с некоторой высоты

Уравнения движения тела:

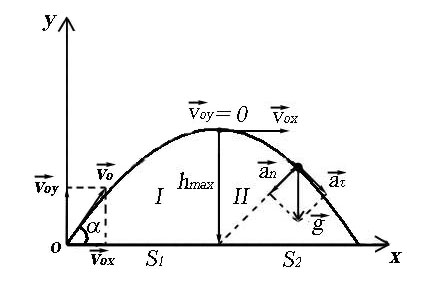
Движение тела, брошенного под углом к горизонту

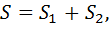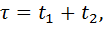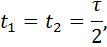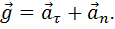Уравнения движения тела на I этапе:

Уравнения движения тела на II этапе:

Максимальная высота подъема тела:

В любой точке траектории скорость:

В момент приземления

I закон Ньютона (закон инерции): существуют такие системы отсчета, относительно которых тело сохраняет состояние покоя или скорость постоянной, если на него не действуют другие тела (или действия других тел на него скомпенсированы).

Тело, не подверженное внешним воздействиям, называется свободным.

Явление сохранения скорости тела постоянной (в частности, равной нулю) называется инерцией.

Системы отсчета, относительно которых тела движутся с постоянной скоростью или покоятся при компенсации внешних воздействий на них, называются инерциальными (ИСО).

Инертность – свойство тел, состоящее в том, что для изменения скорости тела требуется некоторое время. Свойство инертности характеризуется массой.

Масса тела – физическая величина, являющаяся одной из характеристик материи, определяющая ее инерционные (инертная масса) и гравитационные свойства (гравитационная масса).

Воздействие тел друг на друга характеризуется силой.

Сила – векторная физическая величина, являющаяся количественной характеристикой воздействия одного тела на другое.

Если к какому-нибудь телу приложено несколько сил, то сила, равная геометрической сумме всех приложенных к нему сил, называется результирующей силой(принцип суперпозиции):

(2.1)

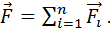
· сила гравитационного взаимодействия (закон Всемирного тяготения):сила, с которой два тела притягиваются друг к другу, прямо пропорциональна массам этих тел и обратно пропорциональна квадрату расстояния между ними

, (2.2)

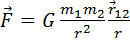
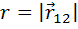
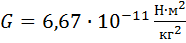
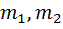
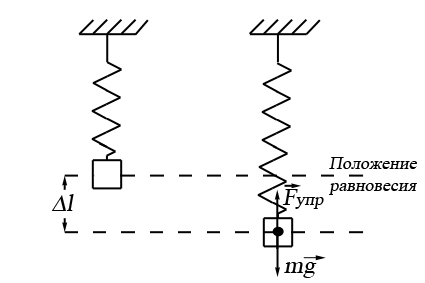
где – радиус – вектор тела 2 относительно тела 1,

— гравитационная постоянная,

— массы взаимодействующих тел;

· сила упругости – сила, возникающая при упругой деформации и направленная в сторону, противоположную перемещению частиц тела при деформации

(2.3)

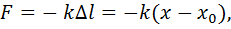
где k – коэффициент упругости (жесткости),

смещение системы из положения равновесия,

координаты тела в конечном и начальном положениях, соответственно;

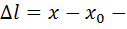
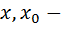
· сила тяжести – сила, с которой Земля притягивает тело:

(2.4)

– ускорение силы тяжести (свободного падения);

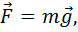
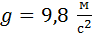
· вес тела – сила, приложенная со стороны тела к опоре или подвесу, ограничивающая свободное перемещение тела в поле сил земного тяготения; вес тела может быть равен, а также больше или меньше силы тяжести:

, (2.5)

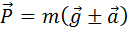
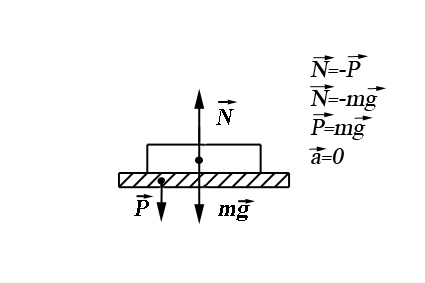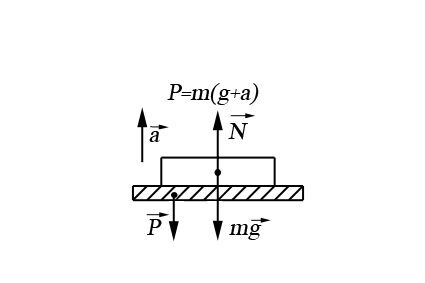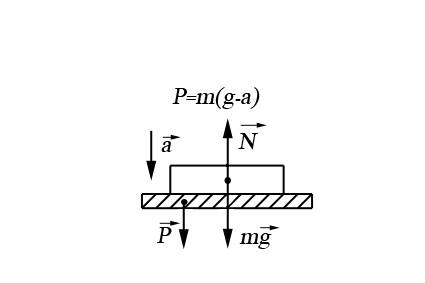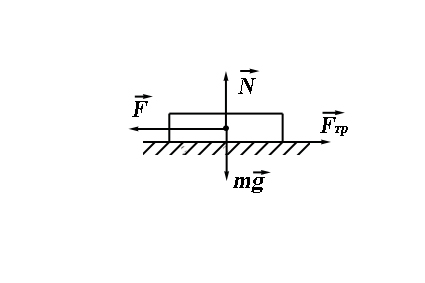
· сила трения – сила, возникающая при движении или попытке движения соприкасающихся тел относительно друг друга и направленные по касательной к трущимся поверхностям в сторону, противоположную движению (сила трения скольжения, сила трения покоя, сила трения качения):

, (2.6)

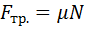
где 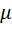— коэффициент трения,

N – сила реакции опоры (нормального давления).

II закон Ньютона (в дифференциальной форме): скорость изменения импульса (производная от импульса по времени) материальной точки равна равнодействующей всех сил, действующих на нее

, (2.7)

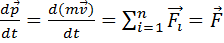
где m – масса точки,

— скорость поступательного движения точки,

– импульс материальной точки ( ).

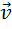
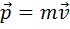
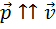
Разделяя переменные в (2.7), и переходя к интегрированию, получим закон изменения импульса точки:

, (2.8)

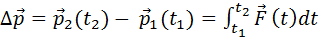
где интеграл 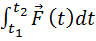называется импульсом силы.

Если , то , и такое движение называется движением по инерции.

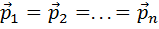
Из (2.8) следует, что изменение импульса материальной точки, равное импульсу силы, имеет геометрический смысл площади криволинейной трапеции.

Выражение (2.8) в проекциях на оси декартовой системы координат:

(2.9)

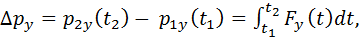
II закон Ньютона (в интегральной форме): ускорение тела пропорционально результирующей силе, действующей на него, и обратно пропорционально его массе:

. (2.10)

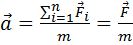
Вектор результирующей силы и ускорения тела направлены в одну сторону ( .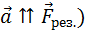

При движении материальной точки по криволинейной траектории, сила в (2.10), действующая на нее, может быть представлена в виде двух составляющих – тангенциальной и нормальной.

(2.11)

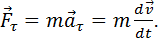
Нормальная составляющая силы

(2.12)

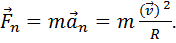
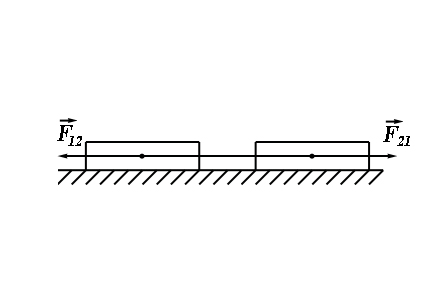
III закон Ньютона: тела действуют друг на друга с силами, равными по модулю и противоположными по направлению (при этом силы приложены к разным телам)

(2.13)

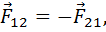
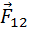
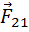
где и — силы, действующие со стороны второй точки на первую, и со стороны первой на вторую, соответственно.

Любое тело или совокупность тел представляет собой множество материальных точек, называемое системой материальных точек.

Если система с течением времени не меняется, то говорят, что она не изменяет своего состояния. Состояние системы материальных точек в механике определяется одновременным заданием координат и скоростей (или импульсов) всех материальных точек, входящих в систему.

Полный импульс системы материальных точек равен векторной сумме импульсов всех материальных точек, входящих в систему

(2.14)

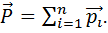
Система материальных точек (тел) называется замкнутой или изолированной, если она не испытывает никакого воздействия со стороны окружающих тел.

Закон сохранения импульса: полный импульс замкнутой (изолированной) системы материальных точек есть величина постоянная, то есть не изменяется со временем

(2.15)

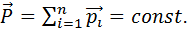
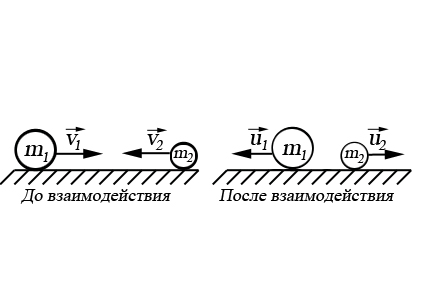
При упругом взаимодействии двух тел выполняется закон сохранения импульса

(2.16)

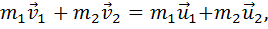
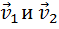
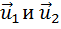
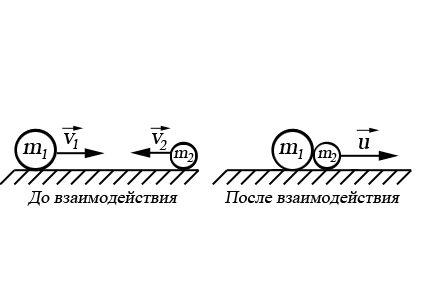
где – скорости первого и второго тела до взаимодействия, соответственно, – скорости первого и второго тела после взаимодействия, соответственно.

При неупругом взаимодействии двух тел выполняется закон сохранения импульса

(2.17)

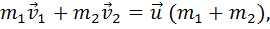
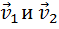
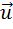
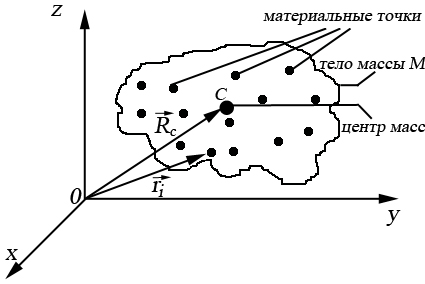
где – скорости первого и второго тела до взаимодействия, соответственно, – скорость первого и второго тел как единого целого после взаимодействия, соответственно.

Центром масс (центром инерции) механической системы материальных точек называется точка пространства, положение которой определяется радиус–вектором

(2.18)

,(2.19)

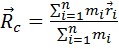
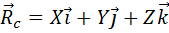
где X, Y, Z – проекции радиус–вектора центра масс,

, , – единичные векторы (орты).

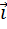
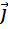
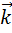
Координаты радиус–вектора центра масс:

,

(2.20)

.

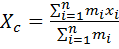
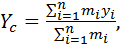
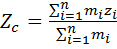
Импульс механической системы материальных точек можно представить как произведение массы системы

на скорость поступательного движения ее центра масс :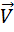

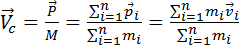
, (2.21)

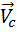
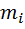
где – скорость поступательного движения центра масс,

– масса i – й материальной точки.

Проекции вектора скорости центра масс на оси декартовой системы координат:

,

(2.22)

,

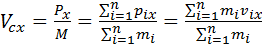
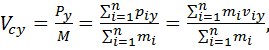
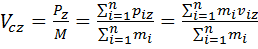
где , , – проекции вектора скорости центра масс,

, , – проекции вектора скорости i – й материальной точки.

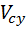
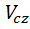
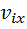
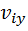
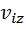
Учитывая выражение для импульса системы материальных точек

и II закона Ньютона (в дифференциальной форме)

,

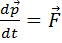
получим выражение II закона Ньютона для системы материальных точек (теорема о движении центра масс): центр масс системы материальных точек движется как материальная точка, масса которой равна суммарной массе всей системы, а действующая сила равна векторной сумме всех внешних сил, действующих на систему

. (2.23)

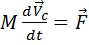
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник