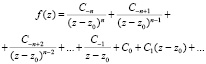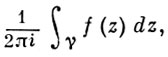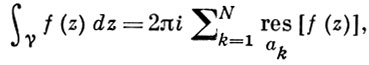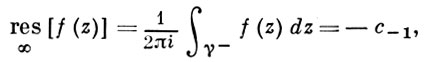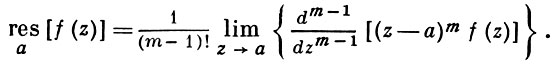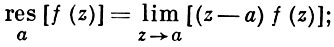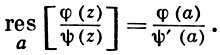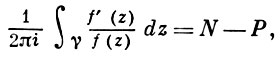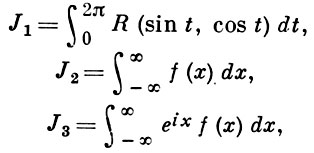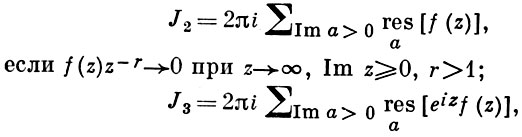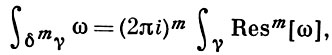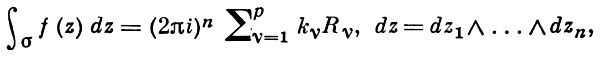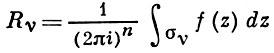вычет функции в полюсе

Вычет функции в полюсе

Обозначается вычет

Вычет функции в конечной изолированной особой точке равен коэффициенту С_-1 при первой отрицательной степени в разложении функции в ряд Лорана в окрестности этой точки, т.е. при 1/(z—z₀) для z₀, принадлежащей области комплексных чисел:

ПРИМЕР 1. Вычисление вычета функции в ее конечных особых точках.

Если конечная особая точка z₀ является устранимой особой точкой функции f(z), то

ПРИМЕР 2. Вычисление вычета в устранимой особой точке.

ПРИМЕР 3. Вычисление вычета в полюсе порядка n.

ПРИМЕР 4. Вычисление вычета в простом полюсе.

ПРИМЕР 5. Вычисление вычета в существенной особой точке.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Источник

Вычет функции в полюсе

Задача определения вычетов функций в особых точках актуальна сама по себе, кроме того, её решение ведет к вычислению криволинейных интегралов по замкнутому контуру. Будем рассматривать функции комплексного переменного, у которых в качестве особенностей выступают только конечные полюсы, и искать вычеты функций в этих полюсах.

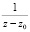
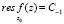
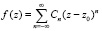
Вычет функции в любой конечной изолированной особой точке равен коэффициенту С-1 при первой отрицательной степени в разложении функции в ряд Лорана в окрестности этой точки [1], т.е. при для z0, принадлежащей области комплексных чисел: . По теореме Лорана [2, 3] о разложении аналитической функции в кольце в ряд по целым степеням имеет место равенство .

Поскольку рассматриваются функции, имеющие в качестве особенностей только полюсы z0, то в выколотой окрестности точки z0 ряд Лорана функции f(z) содержит конечное число членов с отрицательными степенями [4]. То есть, если z0 – полюс n-го порядка, то

Задача состоит в программном вычислении коэффициента С-1. Очевидны соотношения

(*)

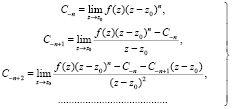
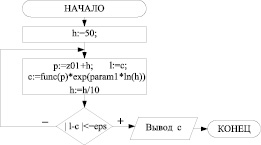
Рис. 1. Структурная схема алгоритма нахождения коэффициентов ряда Лорана с использованием предельного перехода

Последовательное вычисление всех отрицательных коэффициентов ряда Лорана рекуррентно приведет к нахождению С-1. Реализацию предельного перехода алгоритмически предполагалось [5] осуществить следующим образом (рис. 1).

В данном алгоритме используются следующие обозначения: z01 – полюс исходной функции func(z), переменная param1 определяет порядок полюса z01, eps – наперед заданная погрешность вычислений.

Однако таким образом можно точно вычислить лишь коэффициент ряда Лорана с наименьшей отрицательной степенью С-param1. Вычисление следующего коэффициента таким же образом (заменяя лишь выражение для переменной С на выражение, определяющее С-param1+1) дает шесть верных цифр после десятичной точки. Каждый последующий коэффициент вычисляется с большей погрешностью, чем предыдущий; ошибка накапливается, в результате оказывается невозможным точно вычислить вычет функций в полюсах, порядок которых выше второго.

С целью преодоления возникшей трудности предлагается алгоритм приближенного нахождения коэффициентов ряда Лорана, базирующийся на использовании сортировки:

1. На основе сортировки [6, 7], по изложенной в [8, 9] схеме вычисления полюсов комплексных функций находятся все полюсы z0 функции f(z), а также их порядок n [10, 11].

2. Для определения вычета функции в первом из найденных полюсов zk порядка k1 вычисляются необходимые коэффициенты 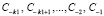из (*) при повторном применении схемы вычисления полюсов исходной функции (уже без учета порядка) в месте спуска к наименьшему значению в окрестности локализованной точки при достаточном сужении области поиска вокруг уже определенного полюса. Иными словами, искомые коэффициенты вычисляются по данной схеме непосредственно по виду выражений, стоящих под знаком предела из (*), по ходу циклического приближения значения z к заново вычисляемому значению z0.

3. Пункт 2 повторяется для каждого из найденных полюсов, пока не будет определен вычет во всех полюсах.

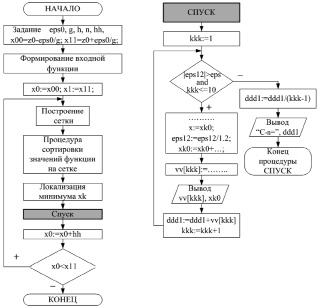
Программная реализация пункта 2 опирается на алгоритм, представленный на рис. 2.

Рис. 2. Упрощенная структурная схема алгоритма приближенного вычисления коэффициента ряда Лорана в окрестности точки z = z0

Как отмечалось выше, область поиска полюсов нужно ограничить небольшой окрестностью вокруг уже известного полюса, что и отражено в блоке описания констант:

eps0 = zz*g; x00 = z0-eps0/g; x11 = z0 + eps0/g.

В ходе численного эксперимента было установлено, что численные значения константы eps0 и граничных точек окрестности поиска x00, x11 зависят друг от друга. Эту зависимость определяет коэффициент g, введенный в блоке описания констант. Значение коэффициента g может быть варьировано в рамках значений от 10-424 до 10-9, что не влияет на точность результата и позволяет произвольно сужать или расширять окрестность поиска.

Значение множителя zz константы eps0 подобрано эвристически в ходе численного эксперимента, оно варьируется в зависимости от порядка полюсов. Однако выбранные значения zz, приведенные в каждом случае в примере 1, остаются постоянными для различных функций, которые имеют одинаковый порядок полюсов.

Приближения к коэффициенту ряда Лорана, который вычисляется по соответствующим формулам из (*), запоминаются в массиве vv, после чего искомый коэффициент представляется как среднее арифметическое значений первых десяти элементов этого массива.

Замечание. Заметим, что весовой одночлен является необходимой компонентой для вычисления порядка полюсов функций в случае отсутствия информации о количестве полюсов, поскольку возможен случай единственности полюса. Отсутствие весовой функции может повлиять на правильность определения порядка полюса, но никак не на само значение полюса. Поэтому использование весового одночлена является излишним при вычислении вычетов функции в полюсах.

Описанный метод ниже иллюстрируется на примере.

Пример. Вычислить вычет функции 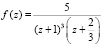в полюсе, имеющем порядок, отличный от 1.

Отметим, что представление исходной функции в таком виде, когда обратная к ней задана разложением на множители, используется с целью иллюстрации, для сравнения результатов работы программы с очевидными значениями полюсов. Исходная функция может быть представлена в виде любой дробно-рациональной функции.

Определим все полюсы исходной функции и их порядок. Как и прежде, изменения произойдут лишь в блоке описания констант и функций:

На вход программы, полный текст которой представлен в [5], подается функция, нули которой совпадают с полюсами исходной функции f(z), она получена при помощи простейших алгебраических преобразований обратной функции к f(z) к виду

,

,

.

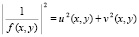
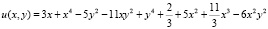
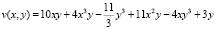
В качестве весовой используется произвольно выбранная функция .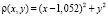

Результаты работы программы приведены в таблице.

Результаты вычисления полюсов функции 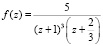с учетом их порядка

Источник

ВЫЧЕТ

Вычет функции в бесконечно удаленной точке n = ∞ для функции f(z), однозначной и аналитической в окрестности этой точки, определяется формулой

При m = 1 (простой полюс) эта формула принимает вид

если f(z) = φ(z)/ψ(z), где φ(z) и ψ(z) регулярны в окрестности точки а, причем для φ(z) точка а есть простой нуль, то

Применение теоремы о В. к логарифмич. производной приводит к важной теореме о логарифмическом вычете: если функция f(z) мероморфна в односвязной области G, а простая замкнутая кривая γ лежит в G и не проходит через нули и полюсы функции f(z), то

В. применяются к вычислению нек-рых определенных интегралов от действительных функций, таких, напр., как

т. е. к вычислению В.;

если f(z) удовлетворяет условиям Жордана леммы.

Теория В. одного переменного разработана в основном О. Коши (A. Cauchy) в 1825-29. Ряд результатов, относящихся к обобщениям теории В. и ее приложениям, был получен Ш. Эрмитом (Ch. Hermite, теорема о сумме В. двоякопериодической функции), П. Лораном (P. Laurent), Ю. В. Сохоцким, Э. Линделёфом (Е. Lindelöf) и др.

Теория вычетов аналитических функций многих комплексных переменных базируется на интегральных теоремах Стокса и Коши-Пуанкаре, позволяющих заменять интеграл от замкнутой формы по одному циклу интегралом от этой формы по другому циклу, гомологичному первому. Начало теории В. функции многих переменных положил А. Пуанкаре [6], к-рый в 1887 впервые обобщил интегральную теорему Коши и понятие В. на функции двух комплексных переменных, показав, в частности, что интеграл от рациональной функции двух комплексных переменных по двумерному циклу, не проходящему через особенности подинтегральной функции, сводится к периодам абелевых интегралов, и применил двойные В. для обоснования двумерного аналога Лагранжа ряда.

— разложение σ по этой базе, то обобщение теоремы о В. имеет вид

Лит.: [1] Маркушевич А. И., Теория аналитических функций, 2 изд., т. 1, М., 1967; [2] Евграфов М. А., Аналитические функции, 2 изд., М., 1968; [3] Привалов И. И., Введение в теорию функций комплексного переменного, 11 изд., М., 1967; [4] Шабат Б. В., Введение в комплексный анализ, М., 1969; [5] Спрингер Д., Введение в теорию римановых поверхностей, пер. с англ., М., 1960; [6] Pоinсаré Н., «Acta math.», 1887, t. 9, 321-380; [7] Лере Ж., Дифференциальное и интегральное исчисления на комплексном аналитическом многообразии, пер. с франц., М., 1961; [8] Фукс Б. А., Введение в теорию аналитических функций многих переменных, М., 1962; [9] Южаков А. П., «Изв. ВУЗов. Матем.», 1964, № 5 (42), с. 149-61; [10] Griffits P. А., «Аnn. Math.», 1969, v. 90, № 3, р. 460-95; [11] Егорычев Г. П., Южаков А. П., «Сиб. матем. ж.», 1974, т. 15, № 5, 1049-60; [12] Южаков А. П., Элементы теории многомерных вычетов, Красноярск, 1975.

Источник

Вычеты

1.Определение вычета и основная теорема о вычетах.

4.Вычет функции относительно бесконечно удаленной точки

1. Определение вычета и основная теорема о вычетах.

Пусть f ( z ) – функция, аналитическая в каждой точке облас-

R в ряд Лорана имеет вид

Определение 1. Вычетом аналитической функции f ( z )

в изолированной особой точке

называется комплексное чис-

ло, равное значению интеграла

содержащему внутри себя

единственную особую точку z 0

Если в выражении c n =

∫ + ( ζ − f ( z ζ ) ) n + 1 d ζ

относительно особой точки

эффициенту при первой отрицательной степени в разложении функции f ( z ) в ряд Лорана.

Теорема 1 (Коши). Пусть f ( z ) есть функция, аналитиче-

ружности попарно не пересекались и целиком лежали в области, ограниченной Γ (рис.1).

Коши для многосвязной области имеем

2. Вычисление вычетов функции.

Пусть точка z 0 является

в точке z 0 можно найти либо по

В первом случае нахождение вычета функции

f ( z ) сводится к вычислению интеграла, во втором случае – к

f ( z ) в ряд Лорана. Рассмотрим вычисле-

ние вычетов в различных особых точках.

Вычисление вычетов функции относительно устранимой особой точки. Пусть z 0 есть устранимая

Вычисление вычетов функции относительно полюса.

Случай 1. Простой полюс.

Так как в правой части равенства находится обыкновенный степенной ряд, то его сумма является непрерывной функцией в

f ( z ) есть частное двух аналити-

ческих в точке z 0 функций

является простым полюсом функции f ( z ) =

z → z 0 h ( z ) − h ( z 0 )

В правой части равенства находится степенной ряд, который равномерно сходится в любом круге, целиком лежащим в его круге сходимости. Поэтому возможно почленное дифференцирование этого ряда любое число раз в круге его сходимости. Дифференцируя последнее равенство ( m − 1 ) раз, имеем

d m − 1 [( z − z 0 − ) m f ( z )] = dz m 1

z 1 = 0 – полюс второго порядка и z 2 = 1 – простой полюс. Тогда имеем

Вычисление вычетов функции относительно существенно особой точки. Пусть точка z 0 является

щественно особой точкой. Разложим данную функцию в ряд Лорана в окрестности точки z = 0

Отсюда находим Res e

3. Логарифмический вычет.

функции f ( z ) называется функция

логарифмической производной функции f ( z ) :

Res ( ln f ( z )) ′ = Res

Теорема 3. Пусть f ( z ) – мероморфная функция в области

► Пусть функция f ( z ) мероморфна в области E и Γ –

f ( z ) являются точки

f ( z ) являются точки

Применяя к функции ( ln f ( z )) ′ основную теорему о вычетах и учитывая теорему 2, получим

2 π 1 i Γ ∫ + f f ′ ( ( z z ) ) dz =

т. е. функция f ( z ) является аналитической в некоторой окрест-

ности бесконечно удаленной точки.

где Γ — замкнутый кусочно-гладкий контур, целиком лежащий в той окрестности бесконечно удаленной точки, в которой функция f ( z ) является аналитической.

Здесь интегрирование по контуру Γ совершается в отрицательном направлении, т. е. так, чтобы при обходе контура бесконечно удаленная точка оставалась слева.

удаленной точки, разложение функции f ( z ) в ряд Лорана имеет

Так как ряд Лорана функции f ( z ) сходится равномерно на

Учитывая, что для k = 0,1, ± 2, L ∫ z k dz = 0 и

Источник