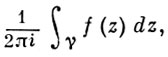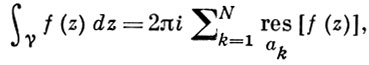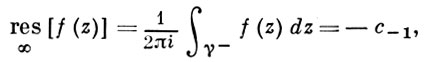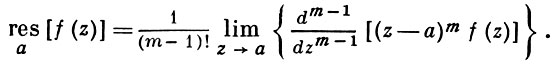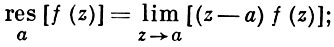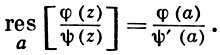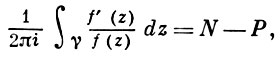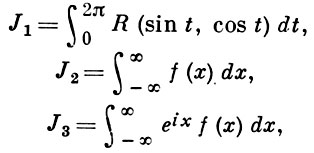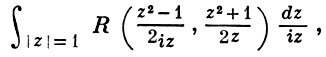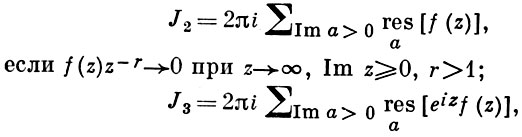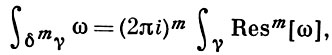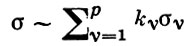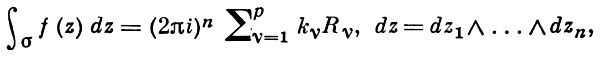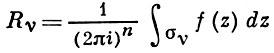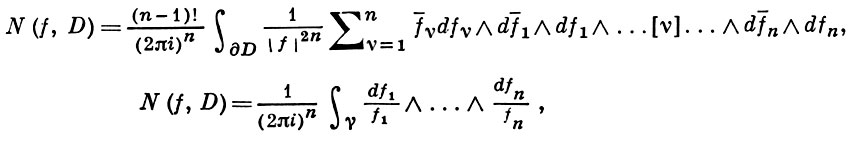вычет функции комплексного переменного
ВЫЧЕТ
Вычет функции в бесконечно удаленной точке n = ∞ для функции f(z), однозначной и аналитической в окрестности этой точки, определяется формулой
При m = 1 (простой полюс) эта формула принимает вид
если f(z) = φ(z)/ψ(z), где φ(z) и ψ(z) регулярны в окрестности точки а, причем для φ(z) точка а есть простой нуль, то
Применение теоремы о В. к логарифмич. производной приводит к важной теореме о логарифмическом вычете: если функция f(z) мероморфна в односвязной области G, а простая замкнутая кривая γ лежит в G и не проходит через нули и полюсы функции f(z), то
В. применяются к вычислению нек-рых определенных интегралов от действительных функций, таких, напр., как
т. е. к вычислению В.;
если f(z) удовлетворяет условиям Жордана леммы.
Теория В. одного переменного разработана в основном О. Коши (A. Cauchy) в 1825-29. Ряд результатов, относящихся к обобщениям теории В. и ее приложениям, был получен Ш. Эрмитом (Ch. Hermite, теорема о сумме В. двоякопериодической функции), П. Лораном (P. Laurent), Ю. В. Сохоцким, Э. Линделёфом (Е. Lindelöf) и др.
Теория вычетов аналитических функций многих комплексных переменных базируется на интегральных теоремах Стокса и Коши-Пуанкаре, позволяющих заменять интеграл от замкнутой формы по одному циклу интегралом от этой формы по другому циклу, гомологичному первому. Начало теории В. функции многих переменных положил А. Пуанкаре [6], к-рый в 1887 впервые обобщил интегральную теорему Коши и понятие В. на функции двух комплексных переменных, показав, в частности, что интеграл от рациональной функции двух комплексных переменных по двумерному циклу, не проходящему через особенности подинтегральной функции, сводится к периодам абелевых интегралов, и применил двойные В. для обоснования двумерного аналога Лагранжа ряда.
— разложение σ по этой базе, то обобщение теоремы о В. имеет вид
Лит.: [1] Маркушевич А. И., Теория аналитических функций, 2 изд., т. 1, М., 1967; [2] Евграфов М. А., Аналитические функции, 2 изд., М., 1968; [3] Привалов И. И., Введение в теорию функций комплексного переменного, 11 изд., М., 1967; [4] Шабат Б. В., Введение в комплексный анализ, М., 1969; [5] Спрингер Д., Введение в теорию римановых поверхностей, пер. с англ., М., 1960; [6] Pоinсаré Н., «Acta math.», 1887, t. 9, 321-380; [7] Лере Ж., Дифференциальное и интегральное исчисления на комплексном аналитическом многообразии, пер. с франц., М., 1961; [8] Фукс Б. А., Введение в теорию аналитических функций многих переменных, М., 1962; [9] Южаков А. П., «Изв. ВУЗов. Матем.», 1964, № 5 (42), с. 149-61; [10] Griffits P. А., «Аnn. Math.», 1969, v. 90, № 3, р. 460-95; [11] Егорычев Г. П., Южаков А. П., «Сиб. матем. ж.», 1974, т. 15, № 5, 1049-60; [12] Южаков А. П., Элементы теории многомерных вычетов, Красноярск, 1975.