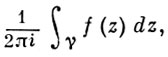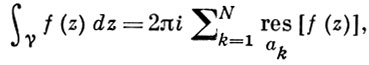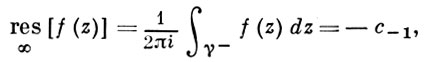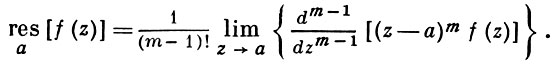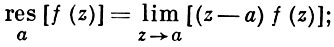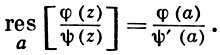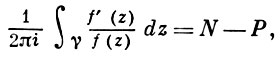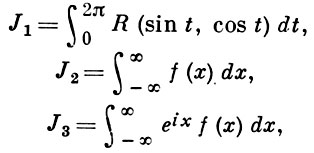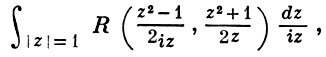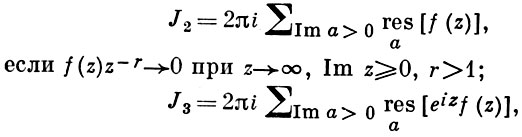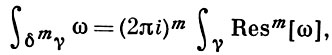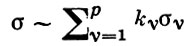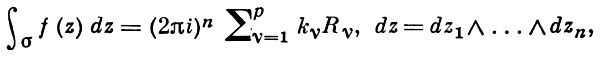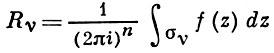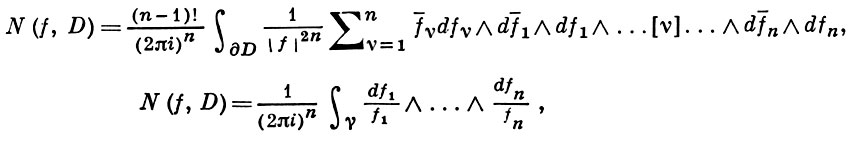вычет в бесконечно удаленной точке пример

20 Вычет функции в бесконечно удаленной особой точке

§20. Вычет функции в бесконечно удаленной особой точке.

Определение. Вычетом аналитической функции f(z) в точке z = ∞ называется значение интеграла , где С – произвольный замкнутый контур, вне которого f(z) – аналитическая и не имеет особых точек, отличных от ∞. Фактически, контур С − является границей окрестности бесконечно удаленной точки, при обходе которой область остается слева. В силу определения коэффициентов ряда Лорана

получаем:

Пример. Вычислить Res. <>

Из полученных формул следует утверждение:

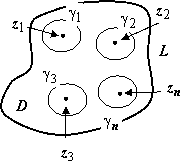
Теорема. Пусть функция f(z) регулярна на расширенной комплексной плоскости, за исключением конечного числа изолированных особых точек z₁,…,z_n−1, z_n = ∞. Тогда

<Пусть контур С содержит внутри себя все конечные особые точки. В силу Т.§19 и последней полученной формулы имеем: . Из второй части равенства следует утверждение теоремы.>

Пример. Рассмотрим последний пример: Res[f,0] = = − Res[f,∞],

Лекция «Федор Михайлович Достоевский» также может быть Вам полезна.

т.е. сумма всех вычетов расширенной комплексной плоскости равна нулю.

Выведенная формула может быть записана следующим образом:

.

В такой форме она применяется как при вычислении вычета в бесконечно удаленной точке,

так и справа налево при вычислении интегралов в том случае, когда внутри контура С находится несколько полюсов высокого порядка, а вычет в бесконечно удаленной точке может быть найден достаточно просто непосредственно.

Замечание. Из последней формулы следует, что вычет функции, имеющей в бесконечно удаленной точке устранимую особенность, может быть отличным от нуля.

Источник

Вычеты. Основная теорема о вычетах

Содержание:

По этой ссылке вы найдёте полный курс лекций по математике:

] в лорановском разложении этой функции в точке z0. Отсюда, в частности, вытекает, что вычет в устранимой особой точке равен нулю. Укажем некоторые формулы для вычисления вычета в полюсе функции /(г).

Поэтому по теореме Коши для многосвязной области имеем Из этой формулы, пользуясь определением вычета получаем требуемое равенство (5). 6.1. Вычет функции относительно бесконечно удаленной точки Говорят, чтофункция f(z) является аналитической в бесконечно удаленной точке z = оо, если функция аналитична вточке С =0. Это следует понимать так: функцию g(0= f (f) можно доопределить до аналитической, положив Например, функция аналитична в точке z = оо, поскольку функция аналитична в точке С = 0.

Возможно вам будут полезны данные страницы:

Пусть функция /(г) аналитична в некоторой окрестности бесконечно удаленной точки (кроме самой точки z = оо). Точка z = оо называется изолированной особой точкой функции /(г), если в некоторой окрестности этой точки нет других особых точек функции f(z). Функция имеет в бесконечности неизолированную особенность: полюсы zk = к-к этой функции накапливаются в бесконечности, если к оо. Говорят, что z — оо является устранимой особой тонкой, полюсом или существенно особой точкой функции f(z) в зависимости от того, конечен, бесконечен или вовсе не существует lim f(z).

Критерии типа бесконечно удаленной точки, связанные с разложением Лорана, изменяюгся по сравнению с критериями для конечных особых точек. Теорема 22. Если z — оо является устранимой особой точкой функции /(z), то лоранов-ское разложение f(z) в окрестности этой точки не содержит полож и тельных степеней z;eaiu z — оо — полюс, то это разложение содержит конечное число положительных степеней z, в случае существенной особенности — бесконечное число положительных степеней z.

При этом лорановским разложением функции /(z) в окрестности бесконечно удаленной точки будем называть разложение в ряд Лорана, сходящийся всюду вне круга достаточно большого радиуса R с центром в точке z — 0 (кроме, быть может, самой точки z — оо). Пусть функция f(z) — аналитична в некоторой окрестности точки z = оо (кроме, быть может, самой этой точки). Вычетом функции /(z) в бесконечности называют величину пае 7 — достаточно большая окружность \z\ = р, проходимая по часовой стрелке (так, что окрестность точки z — оо остается слева, как и в случае конечной точки г = го).

И з этого определения следует, что вычет функции в бесконечности равен коэффициенту при z

Известные тейлоровские разложения функций е1, cosz, sinz, chz, shz можно рассматривать также и как лорановские разложения в окрестности точки z — оо.

Так как все эти разложения содержат бесконечное множество положительных степеней z, то перечисленные функции имеюгвточке z = оо существенную особенность. Теорема 23. Если функция f(z) имеет в расширенной комплексной плоскости конечное число особых точек, то сумма всех ее вычетов, включая и вычет в бесконечности, равна нулю. Так что, если — конечные особые точки функции f

Пример 4:

Вычислить интеграл Полюсами (конечными) подынтегральной функции являются корни zt уравнения гя = —1, которые все лежат внутри окружности В окрестности точки г = оо функция /(z) имеет следующее разложение: ИЗ КОТОРОГО ВИДНО, ЧТО В силу теоремы 6.2. Приложение вычетов к вычислению определенных интегралов. Интегралы от рациональных функций Теорема 24. Пусть f(x) — рациональная функция, т. е. где — многочлены степеней пит соответственно.

Пример 5:

Пример 6. Вычислить интеграл Применяя подстановку z = е,г. после простых преобразований (см. формулы (II)) получим, что Внутри единичного круга при условии находится только один полюс (второго порядка) Вычет функции Интегралы вида гдеД(х) — правильная рациональная дробь, а > 0 — вещественное число. При вычислении таких интегралов часто бывает полезной следующая лемма. Лемма Жордана. Пусть функция f(z) аналитична в верхней полуплоскости исключением конечного числа изолированных особых точек, и при \ стремится к нулю равномерно относительно arg z.

где 7л — верхняя полуокружность Условие равномерного стремления /(г) к нулю означает, что на полуокружности 7R Оценим исследуемый интефал. Замечая, что на 7Л В силу известного неравенства (см. рис. 31) справедливого при (для доказательства достаточно заметить, что и, значит, функция ^ убывает на полуинтервале Сопоставляя формулы (13) и (14), заключаем, что 4 Введем вспомогательную функцию Пример 7. Вычислить интеграл Нетрудно видеть, что если г = х, то Jmh(z) совпадает с подынтегральной функцией.

Отсюда откуда Упражнения Найдите действительную и мнимую части функдаи: Найдите образы действительной и мнимой осей при отображении: Докажи те, что функция непрерывна на всей комплексной плоскости: Пользуясь условиями Коши—Римана, выясните, является ли функция аналитической хотя бы в одной точке или нет: Восстановите аналитическую в окрестности точки 20 функцию /(г) по известной действительной части и (или по известной мнимой части v(x, у)) и значению f(z0):

Покажите, что следующие функци и являются гармоническими: Может ли данная функция быть действительной или мнимой частью аналитической функции Найдите действительную и мнимую части функции: Найдите модуль и главное значение аргумента функции в указанной точке zq: Найдите логарифмы следующих чисел: Решите уравнение: 38. Вычислите интеграл /— линия, соединяющая точки z\ = 0 отрето к прямой, б) дуга параболы ломаная 39. Вычислите интеграл — полуокружность Вычислите интегралы: 43.

Вычислите интеграл / где 7 — верхняя половина окру*« ости |z| = 1 (выбирается Вычеты Основная теорема о вычетах Применение вычетов к вычислению интегралов Вычет функции относительно бесконечно удаленной точки Приложение вычетов к вычислению определенных интегралов Интегралы от рациональных функций Лемма Жордана Вычисление интегралов Френеля ветвь функци и л/z, для которой 44. Вычислите интеграл / ^ dz, где 7 — отрезок прямой, идущий из точки zj = 1 в точку.

Вычислите интегралы: Найдите радиус сходимости ряда: Рашожите функцию в ряд Тейлора и найдите радиус сходимости полученного ряда: постепеням z + I. 55. cosz постепеням 56.—-— постепеням z + 2. 57.—^— постепеням z. 58. sh2 z постепеням z. Найдите нули функции и определите их порядки: z Определите область сходимости ряда: Разложите в ряд Лорана в окрестности точки г = 0: Разяожитс в ряд Лорана в уюзан ном кольце: Найдите особые точки и определит е их характер:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник

Вычет в бесконечно удаленной точке пример

Обозначается вычет

Вычет функции в конечной изолированной особой точке равен коэффициенту С_-1 при первой отрицательной степени в разложении функции в ряд Лорана в окрестности этой точки, т.е. при 1/(z—z₀) для z₀, принадлежащей области комплексных чисел:

ПРИМЕР 1. Вычисление вычета функции в ее конечных особых точках.

Если конечная особая точка z₀ является устранимой особой точкой функции f(z), то

ПРИМЕР 2. Вычисление вычета в устранимой особой точке.

ПРИМЕР 3. Вычисление вычета в полюсе порядка n.

ПРИМЕР 4. Вычисление вычета в простом полюсе.

ПРИМЕР 5. Вычисление вычета в существенной особой точке.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Источник

1.4. Основная теорема о вычетах.

Пусть функция f(z) аналитична во всех точках ограниченной замкнутой области , границей которой является контурL, за исключением конечного числа особых точек z₁, z₂, z₃, …, z_n, расположенных внутри L. Тогда . Док-во. Окружим каждую особою точку z_k, k = 1, 2, …, n контуром γ_k = <z || z − z _k | = ρ _k> таким, чтобы все контуры лежали в области D и не пересекались. В области, ограниченной контурами L, γ ₁, γ ₂, γ ₃, … γ _n, функция аналитична, поэтому по Теореме Коши для многосвязной области. Из определения вычета следует, что , следовательно,, что и требовалось доказать.

Примеры нахождения вычетов

1.5. Бесконечно удалённая особая точка.

Будем считать точку z = ∞ особой точкой любой аналитической функции. В разделе

Источник

ВЫЧЕТ

Вычет функции в бесконечно удаленной точке n = ∞ для функции f(z), однозначной и аналитической в окрестности этой точки, определяется формулой

При m = 1 (простой полюс) эта формула принимает вид

если f(z) = φ(z)/ψ(z), где φ(z) и ψ(z) регулярны в окрестности точки а, причем для φ(z) точка а есть простой нуль, то

Применение теоремы о В. к логарифмич. производной приводит к важной теореме о логарифмическом вычете: если функция f(z) мероморфна в односвязной области G, а простая замкнутая кривая γ лежит в G и не проходит через нули и полюсы функции f(z), то

В. применяются к вычислению нек-рых определенных интегралов от действительных функций, таких, напр., как

т. е. к вычислению В.;

если f(z) удовлетворяет условиям Жордана леммы.

Теория В. одного переменного разработана в основном О. Коши (A. Cauchy) в 1825-29. Ряд результатов, относящихся к обобщениям теории В. и ее приложениям, был получен Ш. Эрмитом (Ch. Hermite, теорема о сумме В. двоякопериодической функции), П. Лораном (P. Laurent), Ю. В. Сохоцким, Э. Линделёфом (Е. Lindelöf) и др.

Теория вычетов аналитических функций многих комплексных переменных базируется на интегральных теоремах Стокса и Коши-Пуанкаре, позволяющих заменять интеграл от замкнутой формы по одному циклу интегралом от этой формы по другому циклу, гомологичному первому. Начало теории В. функции многих переменных положил А. Пуанкаре [6], к-рый в 1887 впервые обобщил интегральную теорему Коши и понятие В. на функции двух комплексных переменных, показав, в частности, что интеграл от рациональной функции двух комплексных переменных по двумерному циклу, не проходящему через особенности подинтегральной функции, сводится к периодам абелевых интегралов, и применил двойные В. для обоснования двумерного аналога Лагранжа ряда.

— разложение σ по этой базе, то обобщение теоремы о В. имеет вид

Лит.: [1] Маркушевич А. И., Теория аналитических функций, 2 изд., т. 1, М., 1967; [2] Евграфов М. А., Аналитические функции, 2 изд., М., 1968; [3] Привалов И. И., Введение в теорию функций комплексного переменного, 11 изд., М., 1967; [4] Шабат Б. В., Введение в комплексный анализ, М., 1969; [5] Спрингер Д., Введение в теорию римановых поверхностей, пер. с англ., М., 1960; [6] Pоinсаré Н., «Acta math.», 1887, t. 9, 321-380; [7] Лере Ж., Дифференциальное и интегральное исчисления на комплексном аналитическом многообразии, пер. с франц., М., 1961; [8] Фукс Б. А., Введение в теорию аналитических функций многих переменных, М., 1962; [9] Южаков А. П., «Изв. ВУЗов. Матем.», 1964, № 5 (42), с. 149-61; [10] Griffits P. А., «Аnn. Math.», 1969, v. 90, № 3, р. 460-95; [11] Егорычев Г. П., Южаков А. П., «Сиб. матем. ж.», 1974, т. 15, № 5, 1049-60; [12] Южаков А. П., Элементы теории многомерных вычетов, Красноярск, 1975.

Источник