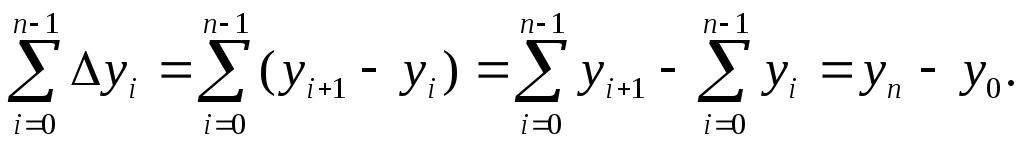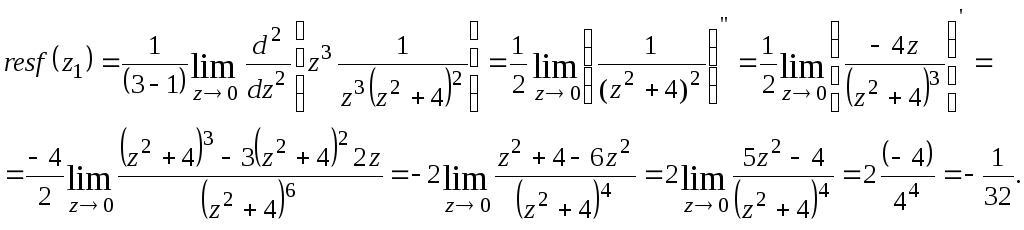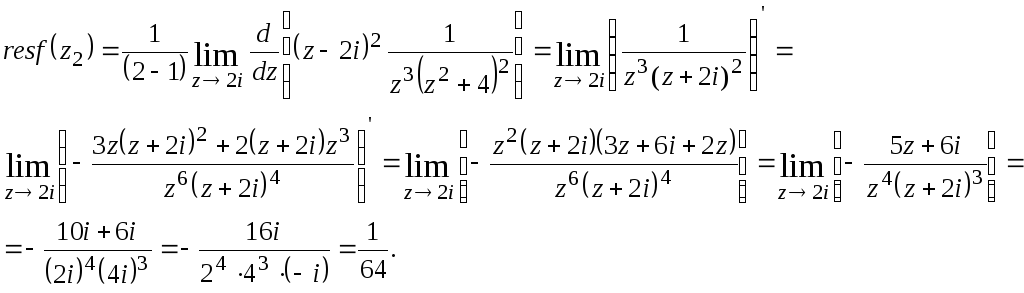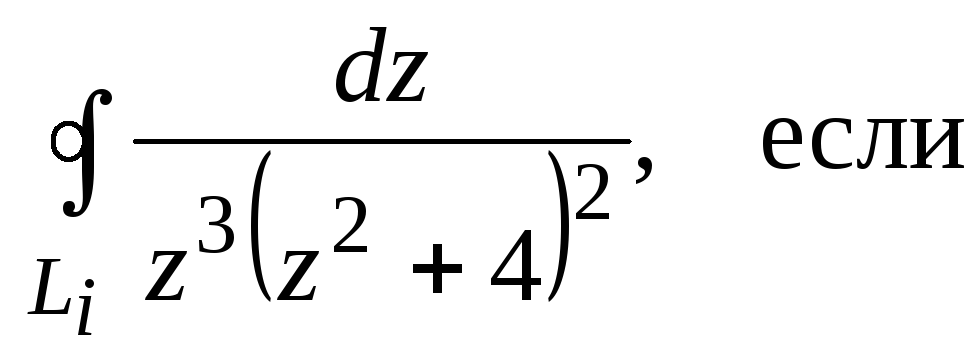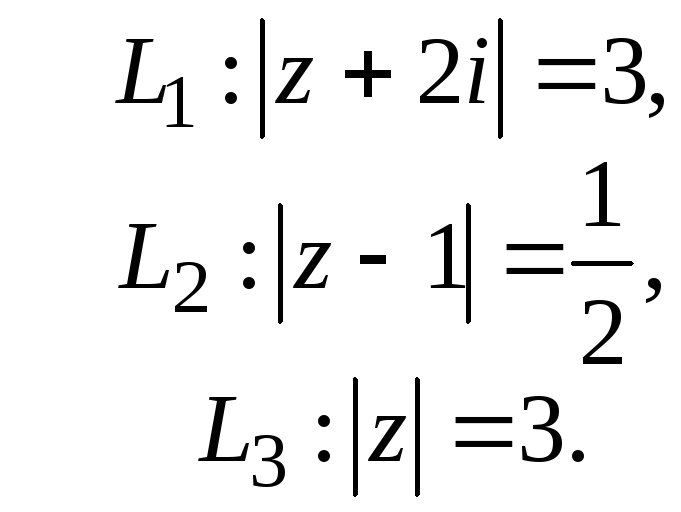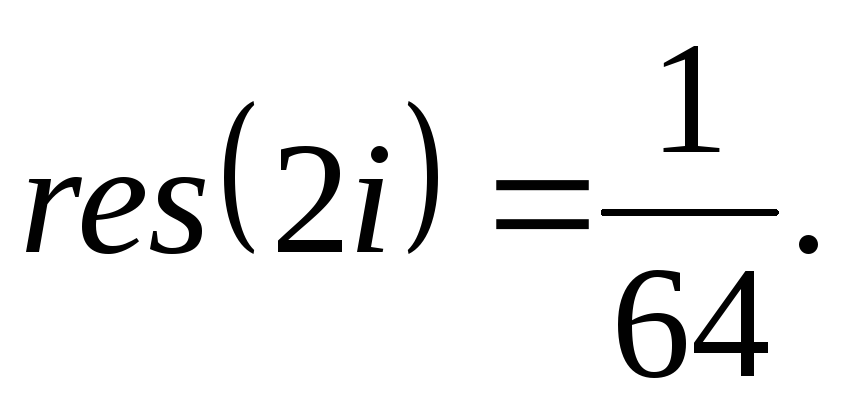вычет в полюсе формула
Вычет в полюсе формула
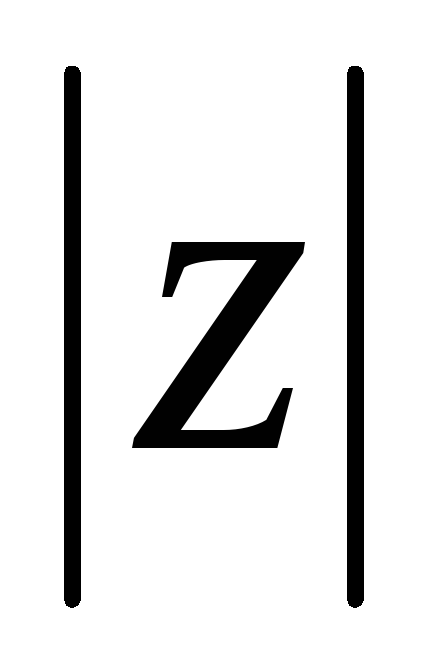
Обозначается вычет
Вычет функции в конечной изолированной особой точке равен коэффициенту С-1 при первой отрицательной степени в разложении функции в ряд Лорана в окрестности этой точки, т.е. при 1/(z—z0) для z0, принадлежащей области комплексных чисел:
ПРИМЕР 1. Вычисление вычета функции в ее конечных особых точках.
Если конечная особая точка z0 является устранимой особой точкой функции f(z), то
ПРИМЕР 2. Вычисление вычета в устранимой особой точке.
ПРИМЕР 3. Вычисление вычета в полюсе порядка n.
ПРИМЕР 4. Вычисление вычета в простом полюсе.
ПРИМЕР 5. Вычисление вычета в существенной особой точке.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Вычеты. Основная теорема о вычетах
Содержание:
По этой ссылке вы найдёте полный курс лекций по математике:
] в лорановском разложении этой функции в точке z0. Отсюда, в частности, вытекает, что вычет в устранимой особой точке равен нулю. Укажем некоторые формулы для вычисления вычета в полюсе функции /(г).
Поэтому по теореме Коши для многосвязной области имеем Из этой формулы, пользуясь определением вычета получаем требуемое равенство (5). 6.1. Вычет функции относительно бесконечно удаленной точки Говорят, чтофункция f(z) является аналитической в бесконечно удаленной точке z = оо, если функция аналитична вточке С =0. Это следует понимать так: функцию g(0= f (f) можно доопределить до аналитической, положив Например, функция аналитична в точке z = оо, поскольку функция аналитична в точке С = 0.
Возможно вам будут полезны данные страницы:
Пусть функция /(г) аналитична в некоторой окрестности бесконечно удаленной точки (кроме самой точки z = оо). Точка z = оо называется изолированной особой точкой функции /(г), если в некоторой окрестности этой точки нет других особых точек функции f(z). Функция имеет в бесконечности неизолированную особенность: полюсы zk = к-к этой функции накапливаются в бесконечности, если к оо. Говорят, что z — оо является устранимой особой тонкой, полюсом или существенно особой точкой функции f(z) в зависимости от того, конечен, бесконечен или вовсе не существует lim f(z).
Критерии типа бесконечно удаленной точки, связанные с разложением Лорана, изменяюгся по сравнению с критериями для конечных особых точек. Теорема 22. Если z — оо является устранимой особой точкой функции /(z), то лоранов-ское разложение f(z) в окрестности этой точки не содержит полож и тельных степеней z;eaiu z — оо — полюс, то это разложение содержит конечное число положительных степеней z, в случае существенной особенности — бесконечное число положительных степеней z.
При этом лорановским разложением функции /(z) в окрестности бесконечно удаленной точки будем называть разложение в ряд Лорана, сходящийся всюду вне круга достаточно большого радиуса R с центром в точке z — 0 (кроме, быть может, самой точки z — оо). Пусть функция f(z) — аналитична в некоторой окрестности точки z = оо (кроме, быть может, самой этой точки). Вычетом функции /(z) в бесконечности называют величину пае 7 — достаточно большая окружность \z\ = р, проходимая по часовой стрелке (так, что окрестность точки z — оо остается слева, как и в случае конечной точки г = го).
И з этого определения следует, что вычет функции в бесконечности равен коэффициенту при z
Известные тейлоровские разложения функций е1, cosz, sinz, chz, shz можно рассматривать также и как лорановские разложения в окрестности точки z — оо.
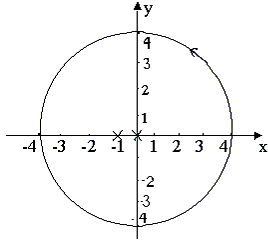
Так как все эти разложения содержат бесконечное множество положительных степеней z, то перечисленные функции имеюгвточке z = оо существенную особенность. Теорема 23. Если функция f(z) имеет в расширенной комплексной плоскости конечное число особых точек, то сумма всех ее вычетов, включая и вычет в бесконечности, равна нулю. Так что, если — конечные особые точки функции f Вычислить интеграл Полюсами (конечными) подынтегральной функции являются корни zt уравнения гя = —1, которые все лежат внутри окружности В окрестности точки г = оо функция /(z) имеет следующее разложение: ИЗ КОТОРОГО ВИДНО, ЧТО В силу теоремы 6.2. Приложение вычетов к вычислению определенных интегралов. Интегралы от рациональных функций Теорема 24. Пусть f(x) — рациональная функция, т. е. где — многочлены степеней пит соответственно. Пример 6. Вычислить интеграл Применяя подстановку z = е,г. после простых преобразований (см. формулы (II)) получим, что Внутри единичного круга при условии находится только один полюс (второго порядка) Вычет функции Интегралы вида гдеД(х) — правильная рациональная дробь, а > 0 — вещественное число. При вычислении таких интегралов часто бывает полезной следующая лемма. Лемма Жордана. Пусть функция f(z) аналитична в верхней полуплоскости исключением конечного числа изолированных особых точек, и при \ стремится к нулю равномерно относительно arg z. где 7л — верхняя полуокружность Условие равномерного стремления /(г) к нулю означает, что на полуокружности 7R Оценим исследуемый интефал. Замечая, что на 7Л В силу известного неравенства (см. рис. 31) справедливого при (для доказательства достаточно заметить, что и, значит, функция ^ убывает на полуинтервале Сопоставляя формулы (13) и (14), заключаем, что 4 Введем вспомогательную функцию Пример 7. Вычислить интеграл Нетрудно видеть, что если г = х, то Jmh(z) совпадает с подынтегральной функцией. Отсюда откуда Упражнения Найдите действительную и мнимую части функдаи: Найдите образы действительной и мнимой осей при отображении: Докажи те, что функция непрерывна на всей комплексной плоскости: Пользуясь условиями Коши—Римана, выясните, является ли функция аналитической хотя бы в одной точке или нет: Восстановите аналитическую в окрестности точки 20 функцию /(г) по известной действительной части и (или по известной мнимой части v(x, у)) и значению f(z0): Покажите, что следующие функци и являются гармоническими: Может ли данная функция быть действительной или мнимой частью аналитической функции Найдите действительную и мнимую части функции: Найдите модуль и главное значение аргумента функции в указанной точке zq: Найдите логарифмы следующих чисел: Решите уравнение: 38. Вычислите интеграл /— линия, соединяющая точки z\ = 0 отрето к прямой, б) дуга параболы ломаная 39. Вычислите интеграл — полуокружность Вычислите интегралы: 43. Вычислите интеграл / где 7 — верхняя половина окру*« ости |z| = 1 (выбирается Вычеты Основная теорема о вычетах Применение вычетов к вычислению интегралов Вычет функции относительно бесконечно удаленной точки Приложение вычетов к вычислению определенных интегралов Интегралы от рациональных функций Лемма Жордана Вычисление интегралов Френеля ветвь функци и л/z, для которой 44. Вычислите интеграл / ^ dz, где 7 — отрезок прямой, идущий из точки zj = 1 в точку. Вычислите интегралы: Найдите радиус сходимости ряда: Рашожите функцию в ряд Тейлора и найдите радиус сходимости полученного ряда: постепеням z + I. 55. cosz постепеням 56.—-— постепеням z + 2. 57.—^— постепеням z. 58. sh2 z постепеням z. Найдите нули функции и определите их порядки: z Определите область сходимости ряда: Разложите в ряд Лорана в окрестности точки г = 0: Разяожитс в ряд Лорана в уюзан ном кольце: Найдите особые точки и определит е их характер: Присылайте задания в любое время дня и ночи в ➔ Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института. Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды. В частности при m=1 получим предыдущую формулу (имеем в виду, что 0!=1, производная нулевого порядка – сама функция); при m=2 (для полюса второго порядка) Особая точка называется существенно особой точкой, если Найти особые точки функции Замечание. При вычислении пределов использовалось правило Лопиталя.● Найти особые точки функции ○f(z) имеет три особых точки: z1=0, z2=2i. Найдем вычеты в этих точках по формуле (2). Вычислить интеграл ○Чтобы вычислить интеграл по замкнутому контуру нужно воспользоваться таким алгоритмом. Определить контур интегрирования на комплексной плоскости, указав положительное направление обхода контура. Найти особые изолированные точки внутри контура интегрирования, определить их тип и вычислить вычеты в этих точках. Вычислить интеграл по теореме Коши о вычетах. В рассматриваемом примере контур интегрирования F(z) имеет две особые изолированные точки (на рис. 2 они обозначены крестами). В примере 2 было установлено, что х1=0 – устранимая особая точка и resf(0)=0, а Вычислить ○Контуры интегрирования изображены на рис. 3. В Примере 3 определенно, что подынтегральная функция имеет три особые изолированные точки z1=0, z2=2i, В третью область, ограниченную окружностью радиусом с центром в начале координат входят все три особые точки, поэтому Р Определение кратчайшего пути на графе и построение минимального Научиться применять алгоритм Дейкстры для определения кратчайшего пути на графах и алгоритм ближайшего соседа для построения остовного дерева. Основные теоретические положения Подробно изложены в разделе 3.1 (см. с.56-59). Построение различных видов ДНФ для булевых функций. Овладеть навыками применения метода Квайна для построения сокращенных ДНФ. Основные теоретические положения Подробное изложение методов см. в разделе 3.2 (с.66-72). 4.2. Методические указания к выполнению лабораторных работ Лабораторная работа 1 Интерполяция функций с равноотстоящими узлами Нахождение аналитического выражения функции, заданной таблицей, используя первую интерполяционную формулу Ньютона. 2. Основные теоретические положения Материал по этой теме приведён в разделе 3 (с.19 – 22) и разделе 4 (с.84 – 87). Здесь следует добавить, что для проверки правильности вычислений конечных разностей удобно использовать их свойство: сумма чисел в каждом столбце разностей равна разности крайних членов предыдущего столбца. Сумма всех разностей первого порядка определяется следующим образом: Аналогично, для разностей других порядков будем иметь:Пример 4:
Пример 5:
Тогда для любого положитыьного а Вычет в полюсе порядка m вычисляется по формуле
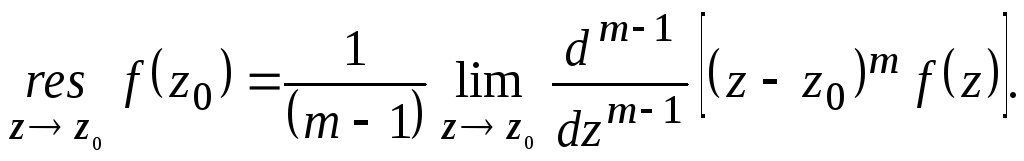
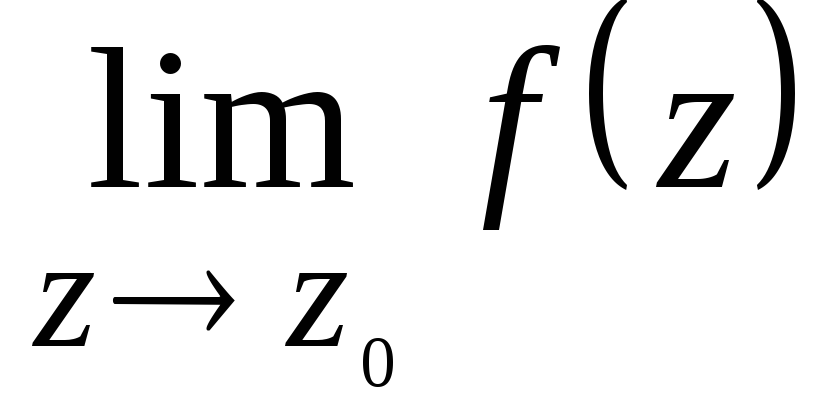
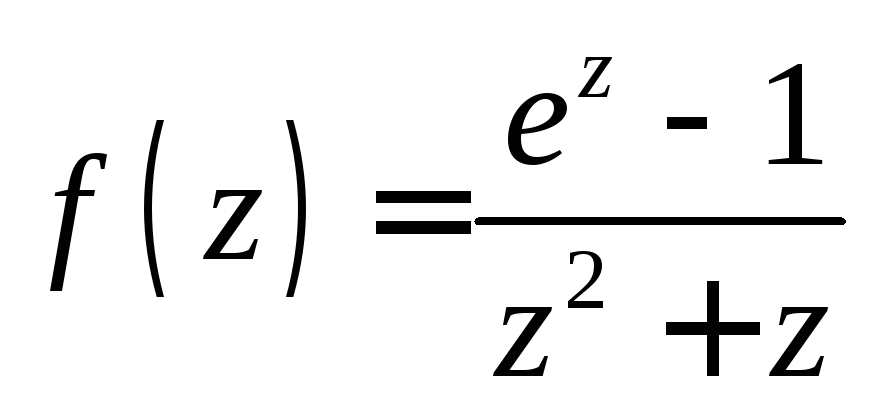

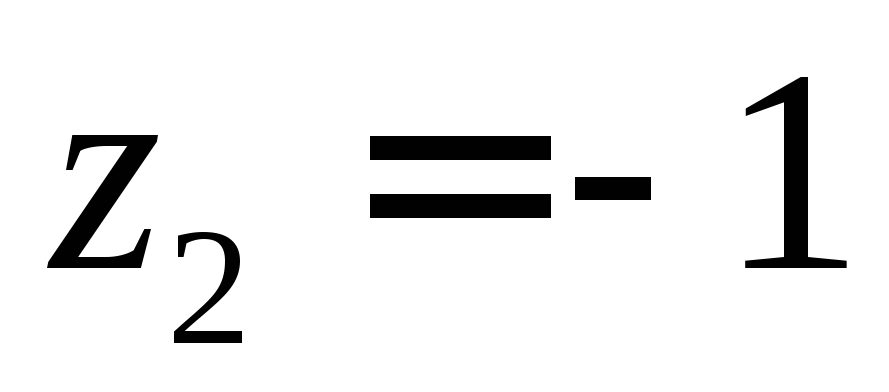
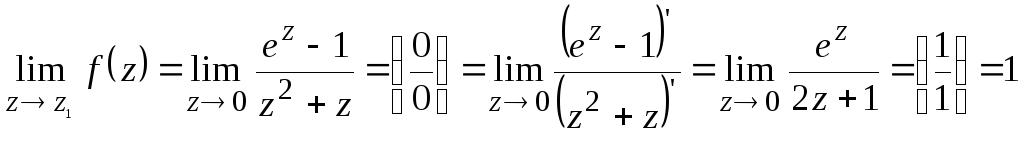
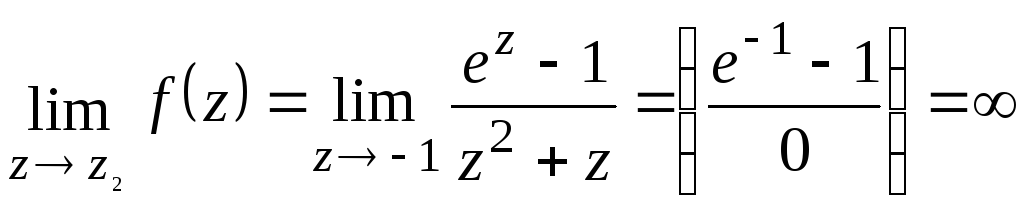
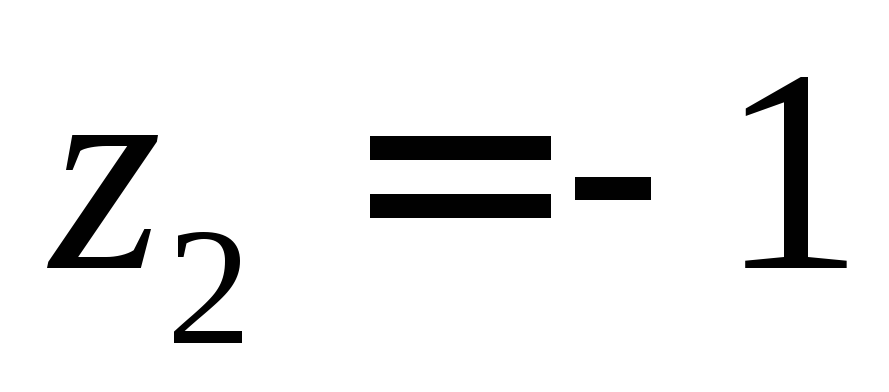
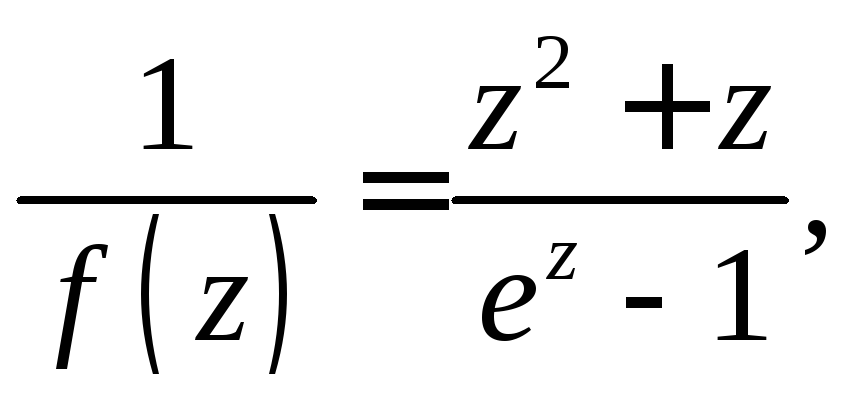
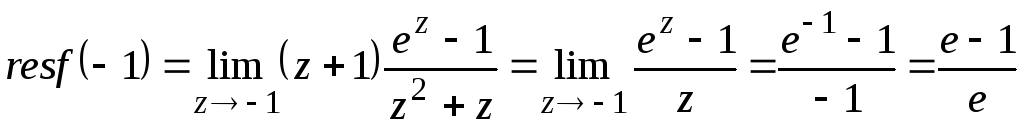

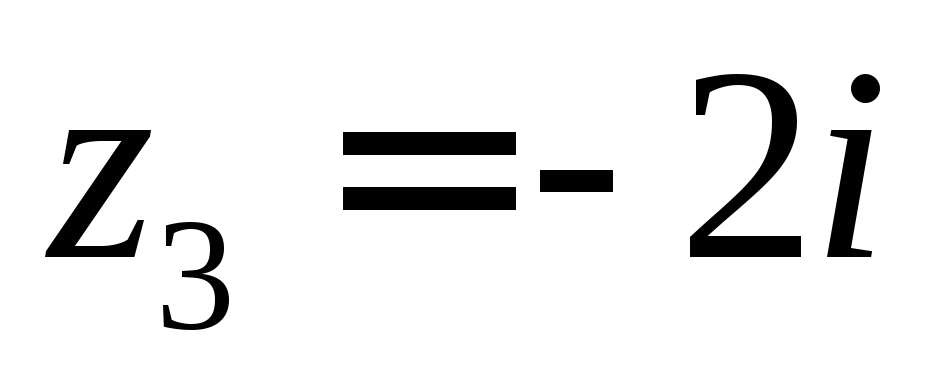






По теореме Коши о вычетах интеграл будет равен
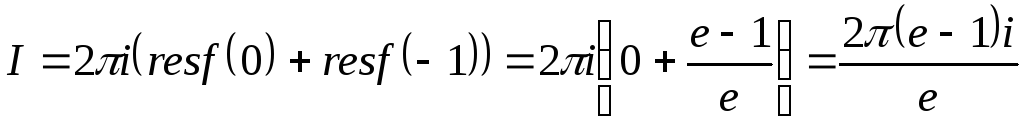
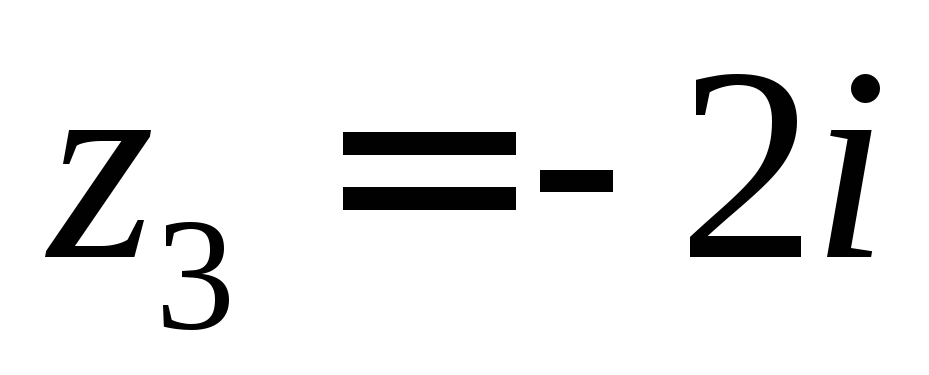
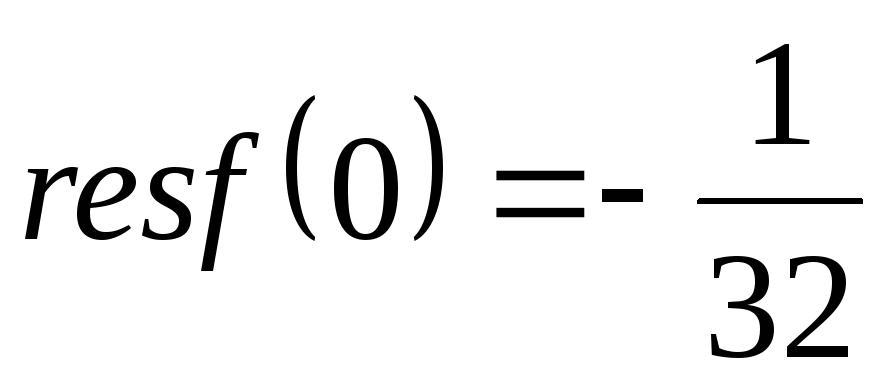

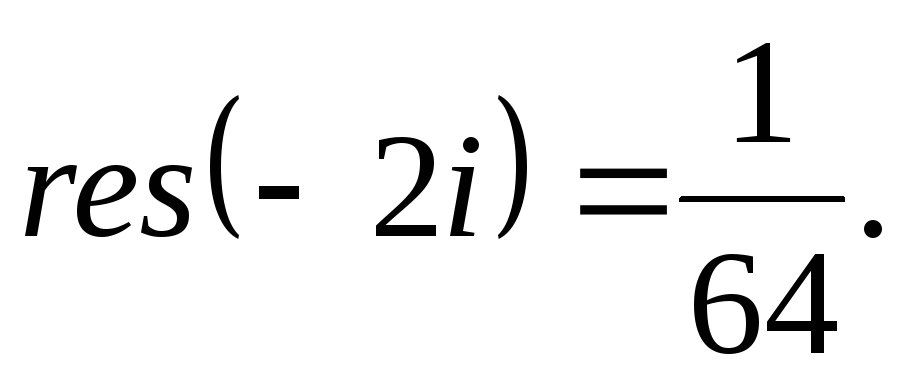

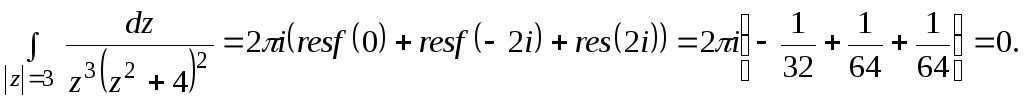
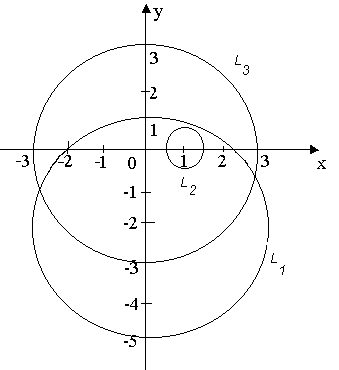
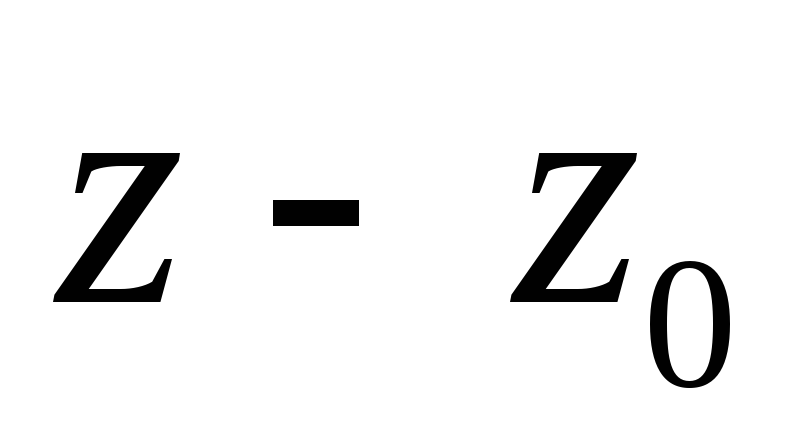
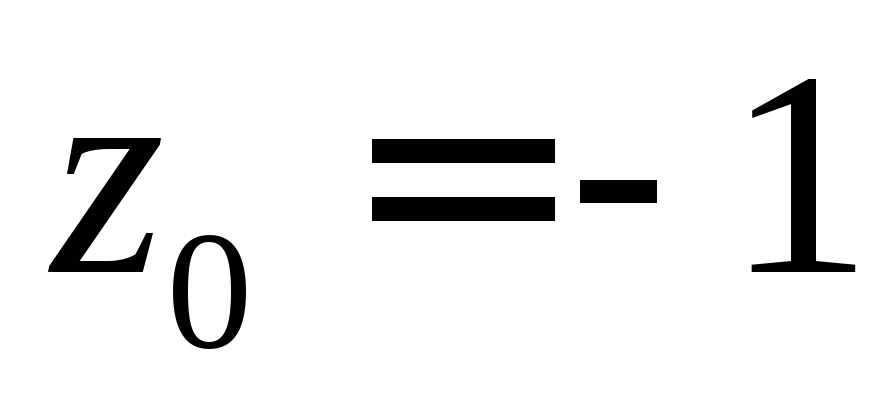
Задание 8