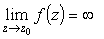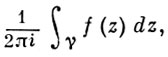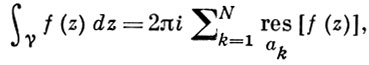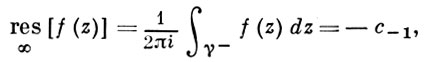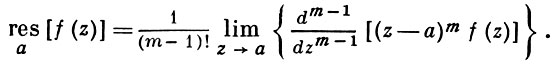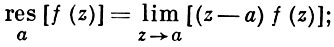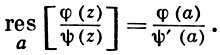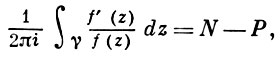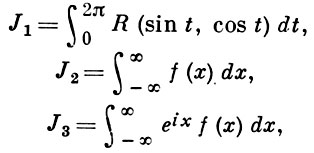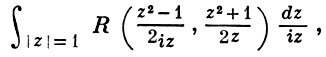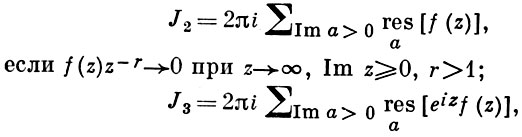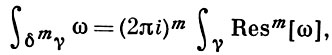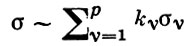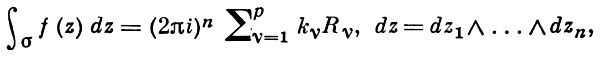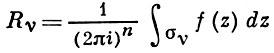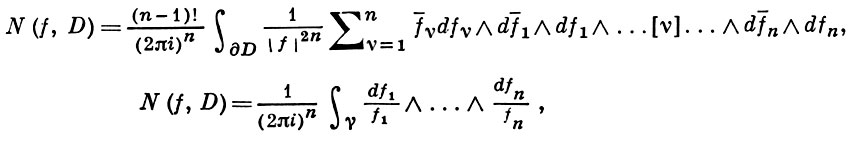вычет в простом полюсе
Вычет в простом полюсе
Обозначается вычет
Вычет функции в конечной изолированной особой точке равен коэффициенту С-1 при первой отрицательной степени в разложении функции в ряд Лорана в окрестности этой точки, т.е. при 1/(z—z0) для z0, принадлежащей области комплексных чисел:
ПРИМЕР 1. Вычисление вычета функции в ее конечных особых точках.
Если конечная особая точка z0 является устранимой особой точкой функции f(z), то
ПРИМЕР 2. Вычисление вычета в устранимой особой точке.
ПРИМЕР 3. Вычисление вычета в полюсе порядка n.
ПРИМЕР 4. Вычисление вычета в простом полюсе.
ПРИМЕР 5. Вычисление вычета в существенной особой точке.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Вычет в простом полюсе
Пусть в разложении f (z) в окрестности z0 главная часть ряда Лорана отсутствует, т.е.
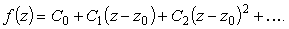 | (6) |
Точка z0 называется простым полюсом, или полюсом первого порядка, если в окрестности c разложение f(z) в ряд Лорана имеет вид :
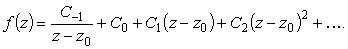 | (7) |
Отметим, что в полюсе первого порядка вычет обязательно отличен от нуля, а
Если разложение в ряд Лорана в окрестности точки z0 имеет вид
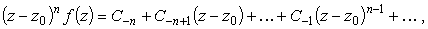 | (11) |
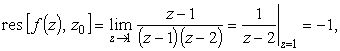 | (13) |
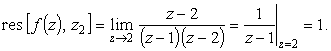 | (14) |
Можно было воспользоваться и формулой (9). А именно
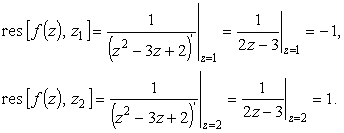 | (15) |
Пример 2.
Найдем вычет в точке z = 0. Точка z = 0 является полюсом третьего порядка, и вычисление вычета нужно производить по формуле (12) с n = 3
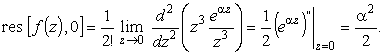 | (16) |
Пример 3.
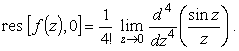 | (17) |
Вычисления производной и тем более предела в этом примере достаточно сложны. Вычет быстрее и проще найти из разложения функции в ряд Лорана. Воспользовавшись известным разложением синуса, получим
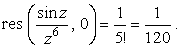 | (19) |
Разложение (18) подтверждает, что точка является полюсом пятого порядка
Найдем вычет в точке z = 0. Здесь мы имеем дело с существенно особой точкой. Вычет определяется из разложения функции в ряд. Имеем
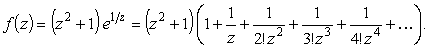 | (20) |
Теперь надо почленно перемножить эти выражения и найти коэффициент C-1
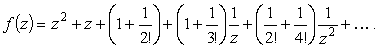 | (21) |
Вычет 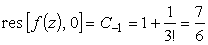
ВЫЧЕТ
Вычет функции в бесконечно удаленной точке n = ∞ для функции f(z), однозначной и аналитической в окрестности этой точки, определяется формулой
При m = 1 (простой полюс) эта формула принимает вид
если f(z) = φ(z)/ψ(z), где φ(z) и ψ(z) регулярны в окрестности точки а, причем для φ(z) точка а есть простой нуль, то
Применение теоремы о В. к логарифмич. производной приводит к важной теореме о логарифмическом вычете: если функция f(z) мероморфна в односвязной области G, а простая замкнутая кривая γ лежит в G и не проходит через нули и полюсы функции f(z), то
В. применяются к вычислению нек-рых определенных интегралов от действительных функций, таких, напр., как
т. е. к вычислению В.;
если f(z) удовлетворяет условиям Жордана леммы.
Теория В. одного переменного разработана в основном О. Коши (A. Cauchy) в 1825-29. Ряд результатов, относящихся к обобщениям теории В. и ее приложениям, был получен Ш. Эрмитом (Ch. Hermite, теорема о сумме В. двоякопериодической функции), П. Лораном (P. Laurent), Ю. В. Сохоцким, Э. Линделёфом (Е. Lindelöf) и др.
Теория вычетов аналитических функций многих комплексных переменных базируется на интегральных теоремах Стокса и Коши-Пуанкаре, позволяющих заменять интеграл от замкнутой формы по одному циклу интегралом от этой формы по другому циклу, гомологичному первому. Начало теории В. функции многих переменных положил А. Пуанкаре [6], к-рый в 1887 впервые обобщил интегральную теорему Коши и понятие В. на функции двух комплексных переменных, показав, в частности, что интеграл от рациональной функции двух комплексных переменных по двумерному циклу, не проходящему через особенности подинтегральной функции, сводится к периодам абелевых интегралов, и применил двойные В. для обоснования двумерного аналога Лагранжа ряда.
— разложение σ по этой базе, то обобщение теоремы о В. имеет вид
Лит.: [1] Маркушевич А. И., Теория аналитических функций, 2 изд., т. 1, М., 1967; [2] Евграфов М. А., Аналитические функции, 2 изд., М., 1968; [3] Привалов И. И., Введение в теорию функций комплексного переменного, 11 изд., М., 1967; [4] Шабат Б. В., Введение в комплексный анализ, М., 1969; [5] Спрингер Д., Введение в теорию римановых поверхностей, пер. с англ., М., 1960; [6] Pоinсаré Н., «Acta math.», 1887, t. 9, 321-380; [7] Лере Ж., Дифференциальное и интегральное исчисления на комплексном аналитическом многообразии, пер. с франц., М., 1961; [8] Фукс Б. А., Введение в теорию аналитических функций многих переменных, М., 1962; [9] Южаков А. П., «Изв. ВУЗов. Матем.», 1964, № 5 (42), с. 149-61; [10] Griffits P. А., «Аnn. Math.», 1969, v. 90, № 3, р. 460-95; [11] Егорычев Г. П., Южаков А. П., «Сиб. матем. ж.», 1974, т. 15, № 5, 1049-60; [12] Южаков А. П., Элементы теории многомерных вычетов, Красноярск, 1975.
Вычеты
1.Определение вычета и основная теорема о вычетах.
4.Вычет функции относительно бесконечно удаленной точки
1. Определение вычета и основная теорема о вычетах.
Пусть f ( z ) – функция, аналитическая в каждой точке облас-
R в ряд Лорана имеет вид
Определение 1. Вычетом аналитической функции f ( z )
в изолированной особой точке
называется комплексное чис-
ло, равное значению интеграла
содержащему внутри себя
единственную особую точку z 0
Если в выражении c n =
∫ + ( ζ − f ( z ζ ) ) n + 1 d ζ
относительно особой точки
эффициенту при первой отрицательной степени в разложении функции f ( z ) в ряд Лорана.
Теорема 1 (Коши). Пусть f ( z ) есть функция, аналитиче-
ружности попарно не пересекались и целиком лежали в области, ограниченной Γ (рис.1).
Коши для многосвязной области имеем
2. Вычисление вычетов функции.
Пусть точка z 0 является
в точке z 0 можно найти либо по
В первом случае нахождение вычета функции
f ( z ) сводится к вычислению интеграла, во втором случае – к
f ( z ) в ряд Лорана. Рассмотрим вычисле-
ние вычетов в различных особых точках.
Вычисление вычетов функции относительно устранимой особой точки. Пусть z 0 есть устранимая
Вычисление вычетов функции относительно полюса.
Случай 1. Простой полюс.
Так как в правой части равенства находится обыкновенный степенной ряд, то его сумма является непрерывной функцией в
f ( z ) есть частное двух аналити-
ческих в точке z 0 функций
является простым полюсом функции f ( z ) =
z → z 0 h ( z ) − h ( z 0 )
В правой части равенства находится степенной ряд, который равномерно сходится в любом круге, целиком лежащим в его круге сходимости. Поэтому возможно почленное дифференцирование этого ряда любое число раз в круге его сходимости. Дифференцируя последнее равенство ( m − 1 ) раз, имеем
d m − 1 [( z − z 0 − ) m f ( z )] = dz m 1
z 1 = 0 – полюс второго порядка и z 2 = 1 – простой полюс. Тогда имеем
Вычисление вычетов функции относительно существенно особой точки. Пусть точка z 0 является
щественно особой точкой. Разложим данную функцию в ряд Лорана в окрестности точки z = 0
Отсюда находим Res e
3. Логарифмический вычет.
функции f ( z ) называется функция
логарифмической производной функции f ( z ) :
Res ( ln f ( z )) ′ = Res
Теорема 3. Пусть f ( z ) – мероморфная функция в области
► Пусть функция f ( z ) мероморфна в области E и Γ –
f ( z ) являются точки
f ( z ) являются точки
Применяя к функции ( ln f ( z )) ′ основную теорему о вычетах и учитывая теорему 2, получим
2 π 1 i Γ ∫ + f f ′ ( ( z z ) ) dz =
т. е. функция f ( z ) является аналитической в некоторой окрест-
ности бесконечно удаленной точки.
где Γ — замкнутый кусочно-гладкий контур, целиком лежащий в той окрестности бесконечно удаленной точки, в которой функция f ( z ) является аналитической.
Здесь интегрирование по контуру Γ совершается в отрицательном направлении, т. е. так, чтобы при обходе контура бесконечно удаленная точка оставалась слева.
удаленной точки, разложение функции f ( z ) в ряд Лорана имеет
Так как ряд Лорана функции f ( z ) сходится равномерно на
Учитывая, что для k = 0,1, ± 2, L ∫ z k dz = 0 и
Вычеты
1.Определение вычета и основная теорема о вычетах.
4.Вычет функции относительно бесконечно удаленной точки
1. Определение вычета и основная теорема о вычетах.
Пусть f ( z ) – функция, аналитическая в каждой точке облас-
R в ряд Лорана имеет вид
Определение 1. Вычетом аналитической функции f ( z )
в изолированной особой точке
называется комплексное чис-
ло, равное значению интеграла
содержащему внутри себя
единственную особую точку z 0
Если в выражении c n =
∫ + ( ζ − f ( z ζ ) ) n + 1 d ζ
относительно особой точки
эффициенту при первой отрицательной степени в разложении функции f ( z ) в ряд Лорана.
Теорема 1 (Коши). Пусть f ( z ) есть функция, аналитиче-
ружности попарно не пересекались и целиком лежали в области, ограниченной Γ (рис.1).
Коши для многосвязной области имеем
2. Вычисление вычетов функции.
Пусть точка z 0 является
в точке z 0 можно найти либо по
В первом случае нахождение вычета функции
f ( z ) сводится к вычислению интеграла, во втором случае – к
f ( z ) в ряд Лорана. Рассмотрим вычисле-
ние вычетов в различных особых точках.
Вычисление вычетов функции относительно устранимой особой точки. Пусть z 0 есть устранимая
Вычисление вычетов функции относительно полюса.
Случай 1. Простой полюс.
Так как в правой части равенства находится обыкновенный степенной ряд, то его сумма является непрерывной функцией в
f ( z ) есть частное двух аналити-
ческих в точке z 0 функций
является простым полюсом функции f ( z ) =
z → z 0 h ( z ) − h ( z 0 )
В правой части равенства находится степенной ряд, который равномерно сходится в любом круге, целиком лежащим в его круге сходимости. Поэтому возможно почленное дифференцирование этого ряда любое число раз в круге его сходимости. Дифференцируя последнее равенство ( m − 1 ) раз, имеем
d m − 1 [( z − z 0 − ) m f ( z )] = dz m 1
z 1 = 0 – полюс второго порядка и z 2 = 1 – простой полюс. Тогда имеем
Вычисление вычетов функции относительно существенно особой точки. Пусть точка z 0 является
щественно особой точкой. Разложим данную функцию в ряд Лорана в окрестности точки z = 0
Отсюда находим Res e
3. Логарифмический вычет.
функции f ( z ) называется функция
логарифмической производной функции f ( z ) :
Res ( ln f ( z )) ′ = Res
Теорема 3. Пусть f ( z ) – мероморфная функция в области
► Пусть функция f ( z ) мероморфна в области E и Γ –
f ( z ) являются точки
f ( z ) являются точки
Применяя к функции ( ln f ( z )) ′ основную теорему о вычетах и учитывая теорему 2, получим
2 π 1 i Γ ∫ + f f ′ ( ( z z ) ) dz =
т. е. функция f ( z ) является аналитической в некоторой окрест-
ности бесконечно удаленной точки.
где Γ — замкнутый кусочно-гладкий контур, целиком лежащий в той окрестности бесконечно удаленной точки, в которой функция f ( z ) является аналитической.
Здесь интегрирование по контуру Γ совершается в отрицательном направлении, т. е. так, чтобы при обходе контура бесконечно удаленная точка оставалась слева.
удаленной точки, разложение функции f ( z ) в ряд Лорана имеет
Так как ряд Лорана функции f ( z ) сходится равномерно на
Учитывая, что для k = 0,1, ± 2, L ∫ z k dz = 0 и