вычет в существенно особой точке примеры

Вычет в существенно особой точке примеры

> endstream endobj 14 0 obj 884 endobj 12 0 obj >> /Contents 13 0 R /CropBox [0 0 612 792] >> endobj 16 0 obj > stream GauHKbHBVY%,DFJs54t9Kd-2oJ>0jP49B&_]*ko;]-uB-2uW]4&ugYW9Q#_3M](4-;rf)NDm/>f 9re > XK8JK2ThKMOC _fD_J&q.. UcfbZ%OIBi)eE»lDiAfA#kC2ncqf0eOP26AL6 1\S4Oar4okBHY$=\;j#Kh#*40 KU>56FNOdK, B.,NgFN/:lXm!PC%XR&IpYQu24&nrJI4.(Y?)Ti»K*d 8S»#e?Nin??6V#`@D6_ZSn/)]h,Ki-g_hqhZ$»[T»H»+&u)HqU0e=XoJ K@@mfH2)$=\ ‘Fr,%(dN>rn0U#uF4Q3^b1A>1.PBEU#»M=Je^8X.?WR&qetpO,=7#qiJ,-[UrWZS(42pk>Kr^’J 5rK3E 19S\HLls88(q+8uErIb0GW

> endstream endobj 62 0 obj > stream Gar’$_.pkA%#44r$6@kgEOp54V.5TSgX351E+C7N1pTuK6f*94;Grmt`o@»_s-Cp+q/»\20]*MI V$+JE-T$N[OJ&AbF)h0Zk:sZ]FiVnL_C41l;kgPU5!W,!H)N\K=l=68MbcBc\Vh^&4M]q=dV@[b 0g9:s:/F8_K;2ak]%VD8,@u5a:5r2):Wl>’eT0O+0fYVr72!cG’ih556hR9U(W>a6?>«oj0+`L ^JF/$HS3SfR[E9n?B[`>e,C(:`(]:c#IiZ*ci=%G

> endstream endobj 67 0 obj > stream Gar’$_.pkA%#44r$6@kgEOp54V.5TSgX351E+C7N1pTuK6f*94;Grmt`o@»_s-Cp+q/»\20]*MI V$+JE-T$N[OJ&AbF)h0Zk:sZ]FiVnL_C41l;kgPU5!W,!H)N\K=l=68MbcBc\Vh^&4M]q=dV@[b 0g9:s:/F8_K;2ak]%VD8,@u5a:5r2):Wl>’eT0O+0fYVr72!cG’ih556hR9U(W>a6?>«oj0+`L ^JF/$HS3SfR[E9n?B[`>e,C(:`(]:c#IiZ*ci=%G

> endstream endobj 70 0 obj 273 endobj 2 0 obj > endobj 3 0 obj > endobj xref 0 71 0000000000 65535 f 0000000010 00000 n 0000166967 00000 n 0000167022 00000 n 0000001339 00000 n 0000000210 00000 n 0000001316 00000 n 0000040642 00000 n 0000086675 00000 n 0000002389 00000 n 0000001531 00000 n 0000002366 00000 n 0000003589 00000 n 0000002582 00000 n 0000003566 00000 n 0000005211 00000 n 0000003783 00000 n 0000005187 00000 n 0000012757 00000 n 0000005405 00000 n 0000012733 00000 n 0000015966 00000 n 0000012951 00000 n 0000015942 00000 n 0000018082 00000 n 0000016160 00000 n 0000018058 00000 n 0000021281 00000 n 0000018276 00000 n 0000021257 00000 n 0000022627 00000 n 0000021475 00000 n 0000022603 00000 n 0000024564 00000 n 0000022811 00000 n 0000024540 00000 n 0000027726 00000 n 0000024758 00000 n 0000027702 00000 n 0000031310 00000 n 0000027920 00000 n 0000031286 00000 n 0000034144 00000 n 0000031504 00000 n 0000034120 00000 n 0000037825 00000 n 0000034338 00000 n 0000037801 00000 n 0000040448 00000 n 0000038019 00000 n 0000040424 00000 n 0000040799 00000 n 0000085734 00000 n 0000041951 00000 n 0000042169 00000 n 0000086652 00000 n 0000086832 00000 n 0000140677 00000 n 0000088158 00000 n 0000088376 00000 n 0000141702 00000 n 0000141883 00000 n 0000153949 00000 n 0000142098 00000 n 0000142319 00000 n 0000154323 00000 n 0000154504 00000 n 0000166570 00000 n 0000154719 00000 n 0000154940 00000 n 0000166944 00000 n trailer > startxref 167190 %%EOF

Источник

Вычет в устранимой особой точке равен нулю

Это следует из определения устранимой особой точки: главная часть ряда Лорана отсутствует, все коэффициенты с отрицательными индексами равны нулю, A_-1 = 0.

Вычеты в полюсах.

(z − a) f( z) = A _-1 + A ₀(z − a) + A ₁(z − a) 2 + A ₂(z − a) 3 + …,

.

. (11)

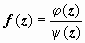
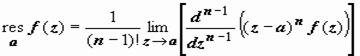
Для того чтобы удалить особенность в точке а, умножим f(z) на

+ A ₀(z − a) n + A ₁(z − a) n + 1 + ….

Теперь, чтобы убрать первые члены этой формулы и добраться до A _-1, дифференцируем это произведение n-1 раз:

, ,
, , откуда и следует доказываемая формула.

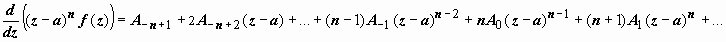
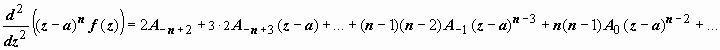
Вычет в существенно особой точке находится из разложения функции в ряд Лорана.

:

.
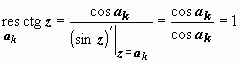
4. .
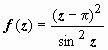
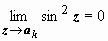
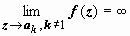
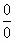
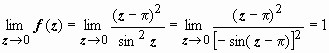
Особые точки – те, в которых sin z = 0: a_k = k π. В этих точках предел знаменателя ; во всех точках a_k, за исключением a ₁ = π, числитель отличен от нуля, поэтому

, следовательно, эти точки – полюса. Для определения порядка этих полюсов найдём порядок нуля знаменателя: ψ(z) = sin 2 z, ψ(a _k ) = 0; ψ′ (z) = sin 2z, ψ′ (a_k ) = 0; ψ″ (z) = 2 cos 2z, ψ′ (a_k ) = 2 ≠ 0, следовательно, эти полюса имеют второй порядок (при k ≠ 1). В точке a ₁ = π функция представляет собой неопределённость , однако, если вспомнить, что sin z = sin(π − z) = − sin(z − π), эта неопределённость раскрывается просто: ,

(к последнему пределу применяем правило Лопиталя) .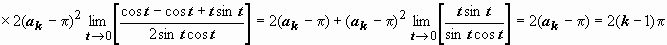

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Вычет в существенно особой точке примеры

Обозначается вычет

Вычет функции в конечной изолированной особой точке равен коэффициенту С_-1 при первой отрицательной степени в разложении функции в ряд Лорана в окрестности этой точки, т.е. при 1/(z—z₀) для z₀, принадлежащей области комплексных чисел:

ПРИМЕР 1. Вычисление вычета функции в ее конечных особых точках.

Если конечная особая точка z₀ является устранимой особой точкой функции f(z), то

ПРИМЕР 2. Вычисление вычета в устранимой особой точке.

ПРИМЕР 3. Вычисление вычета в полюсе порядка n.

ПРИМЕР 4. Вычисление вычета в простом полюсе.

ПРИМЕР 5. Вычисление вычета в существенной особой точке.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Источник